基于Cluster态的n位量子态共享方案

2020-06-12夏红红汪学明杨万鑫

计算机工程与设计 2020年6期

夏红红，汪学明，杨万鑫

(贵州大学计算机科学与技术学院，贵州贵阳 550025)

0 引言

量子密码的安全性完全运用量子力学的基本原理，成功解决了NP和RSA等问题。目前来说，量子密码学可分为量子密钥分配、量子秘密共享等方向。

量子秘密共享是密码学的一个重要分支，主要是解决信息安全等问题。张建中等提出了两个基于四粒子纠缠态的量子秘密共享方案，所提出的方案是高效且安全可靠的[1]；高明等提出了量子多方秘密共享方案，这使得所有的对称纠缠态都可以通过隐形传态来完成秘密共享协议[2]。量子秘密共享经过多年的研究，不论是在实验还是理论研究方面，都取得了很多成果[3-10]。

Cluster态是一种不同于GHZ态和W态的纠缠团簇态。它不仅包含了GHZ态和W态的纠缠态性质，还具有最大连通性和纠缠顽固性[4]，很难被局域操作所破坏，便于实验实现，被广泛应用为量子通信信道。在此基础上，本文提出了两个基于Cluster态的n位量子态秘密共享方案，一个是四粒子Cluster态，另一个是五粒子Cluster态。在方案一中，发送方Alex对自己所持有的粒子进行bell测量，若Alex和Bess同意Chalie恢复未知量子态，Bess进行bell测量，Chalie只需要对自己持有的粒子进行相应的幺正变换即可。方案二中，同样进行两次bell测量，引入辅助粒子进行CNOT操作即可。从本文的计算中可知任何一个代理者在其他两方协助下可以实现任意n位量子态的共享。本文的两个方案操作简单且不受共享态位数的影响，完全基于量子纠缠的量子隐形传态的方式，理论上的成功概率可达100%。最后，对提出的两个基于Cluster态的n位量子态秘密共享方案进行了安全性分析。

1 四粒子Cluster态的n位量子态的秘密共享方案

1.1 两位量子态的秘密共享方案

有3名参与者Alex、Bess和Chalie共同参与量子秘密的共享，其中Alex发送秘密，发送一个未知的两位量子态

φab=α00ab+β11ab

(1)

将一个四粒子Cluster态作为量子信道，四粒子Cluster态的形式为

(2)

Alex拥有粒子1，Bess拥有粒子2和粒子3，Chalie拥有粒子4，则量子态消息与共享的四粒子Cluster态的复合系统可表示为

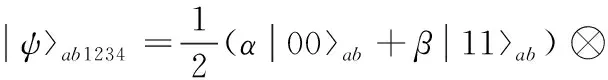
(3)

Alex对自己手中的粒子1和a进行bell测量，公布测量结果之后，Bess和Chalie手中粒子的状态将会塌缩到下列4种状态之一

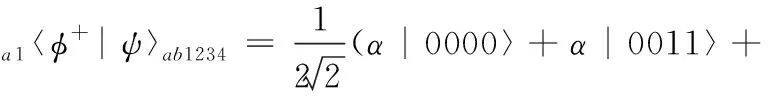
(4)

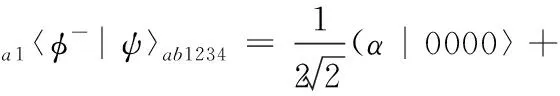
(5)

(6)

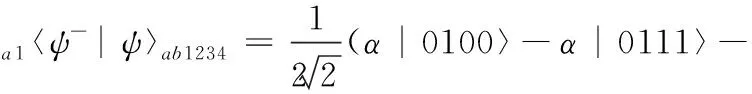
(7)

不失一般性，假设 Alex的测量结果为|φ+a1，则粒子b,2,3,4的态将会塌缩到

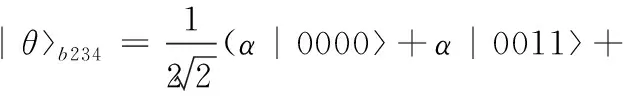
(8)

为了恢复未知量子态，需要将粒子2和粒子3进行bell测量，得到结果为

假设Alex和Bess同意Chalie恢复这个两粒子纠缠态的信息，Chalie只需要对自己持有的粒子4进行相应的幺正变换即可。同样的，假设Alex的测量结果为式φ-a1，则粒子b,2,3,4的态将会塌缩到

(9)

同样的将粒子2和粒子3做bell测量，得到结果为

和上面的步骤一样，Chalie对粒子4进行相应的幺正变换即可恢复初始量子态。具体结果见表1。

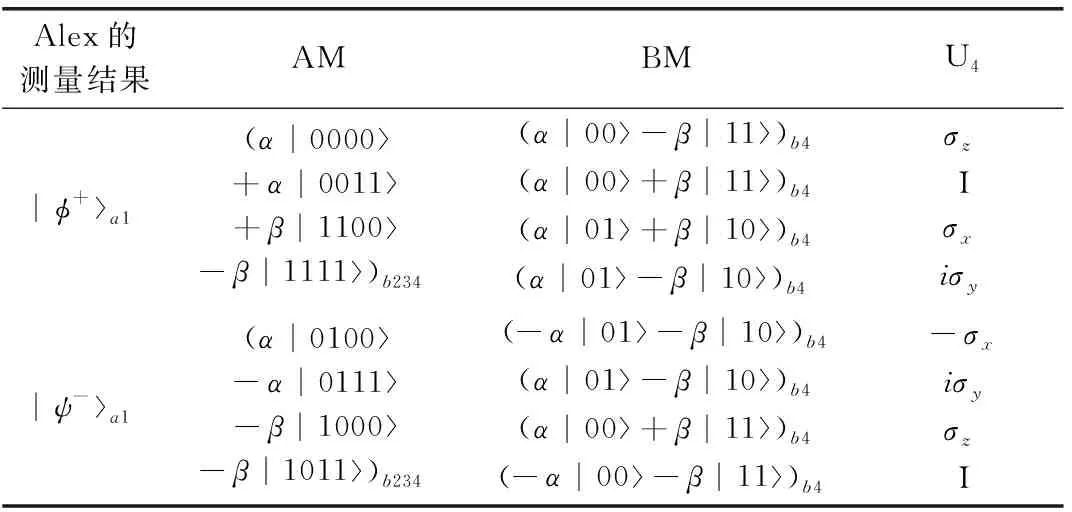
表1 四粒子Cluster态中共享两位量子态秘密结果汇总

1.2 三位量子态的秘密共享方案

为了保证量子信道一致，仍然利用该信道实现未知三位量子态的秘密共享。

此时Alex所要发送的态为

|φabc=α|000abc+β|111abc

(10)

则量子态消息与共享的四粒子Cluster态的复合系统可表示为

(11)

同样的，将粒子a和粒子1，粒子2和粒子3进行bell测量，剩余粒子将塌缩到

为了恢复未知的三位量子态，Chalie只需要对自己持有的粒子4进行相应的幺正变换即可。

1.3 n位量子态的秘密共享方案

此时Alex所要发送的态为

|φabc…n=α|000abc…n+β|111abc…n

(12)

则量子态消息与共享的四粒子Cluster态的复合系统可表示为

(13)

将粒子粒子a和粒子1，粒子2和粒子3进行bell测量，剩余粒子将塌缩到

首先将粒子1和粒子a进行bell测量消去，在剩余bc…n234粒子中，由于粒子2和粒子3的粒子组合不会因为未知量子态发生改变而变，同样的，和上述方案相同，将粒子2和粒子3进行bell测量消去，剩余bc…n4粒子，在原来的未知量子态中，由于a参与了bell测量消去，还剩余n-1个粒子，经过纠缠变换，Alex的态转移到了粒子4上，为了恢复未知的n位量子态，Chalie只需要对自己持有的粒子4进行相应的幺正变换即可。具体结果见表2。

表2 四粒子Cluster态中共享n位量子态秘密结果汇总

在表2中，AM表示Alex公布测量结果时，剩余粒子塌缩的态，BM表示将粒子2和粒子3进行bell测量后的结果。

2 五粒子Cluster态的n位量子态的秘密共享方案

2.1 两位量子态的秘密共享方案

同样的该3名参与者Alex、Bess和Chalie共同恢复秘密，现在Alex给其中一人发送一个未知的两量子态

|θab=α|00ab+β|11ab

(14)

共享的五粒子Cluster态为

(|00000+|00111+|11101+|11010)12345

(15)

则量子态消息与共享的五粒子Cluster态的复合系统可表示为

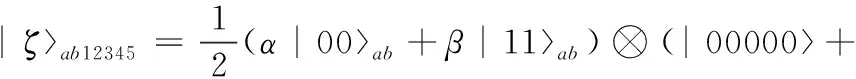
(16)

首先将粒子a和粒子4进行bell测量，得到

(17)

(18)

(19)

(20)

同样的，以式(17)为例，将粒子b和粒子3进行bell测量，得到

(21)

(22)

(23)

(24)

表3 五粒子Cluster态中共享两位量子态秘密结果汇总

CM表示将粒子b和粒子3进行bell测量的结果，DM表示将粒子1和粒子2进行单粒子态测量的结果，U5表示粒子5需要进行的幺正变换。

2.2 三位量子态的秘密共享方案

为了方便研究与阐述，仍然运用五粒子Cluster态为量子信道实现未知三位量子态的秘密共享。

此时Alex所要发送的三位量子态为

|θabc=α|000abc+β|111abc

(25)

则量子态消息与共享的五粒子Cluster态的复合系统可表示为

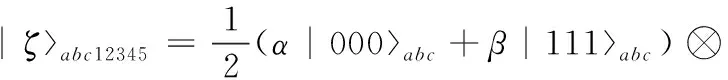
(26)

将粒子a和粒子4进行bell测量，得到

(27)

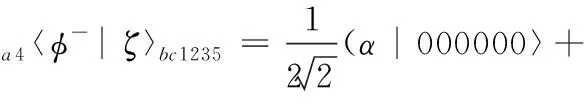
(28)

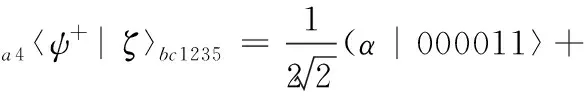
(29)

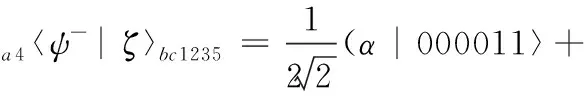
(30)

同样的，以式(27)为例，将粒子b和粒子3进行bell测量，得到

(31)

(32)

(33)

(34)

图1 将(α|00+β|11)c5变换至α|000+β|111

2.3 n位量子态的秘密共享方案

此时Alex所要发送的态为

|φabc…n=α|000abc…n+β|111abc…n

(35)

则量子态消息与共享的五粒子Cluster态的复合系统可表示为

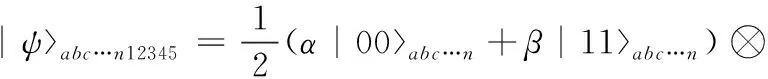
(36)

将粒子(a，4)，(b,3)进行bell测量，剩余粒子将塌缩到

经过两次bell测量消去4个粒子(每次bell测量可消去两个粒子)之后，在剩余粒子中，对粒子1和粒子2分别进行单粒子态测量，最终剩余粒子总是比未知粒子少一个，通过引入辅助粒子的方法，实施一个CNOT操作，经过量子线路最后都能恢复到初始未知量子态。具体结果见表4。

表4 五粒子Cluster态中共享n位量子态秘密结果汇总

3 安全性分析

当攻击者实施截获重发攻击时，可验证信道的安全性。

(α|0000+α|0011+β|1100-β|1111)b234⊗
|0e=(α|00000+α|00110+
β|11000-β|11110)b234e

(α|0000+α|0011+β|1100-β|1111)b234⊗
|1e=(α|00001+α|00111+
β|11001-β|11111)b234e

若测量结果为|ψ+23，则剩余粒子将会塌缩到(α|01+β|10)b4|1e，仍看出Eve未获取到任何有用信息。

假设Bess不诚实，它无法通过局域操作的方法窃听发送方的秘密信息；Bess没有相关粒子的信息只能进行猜测，随着猜测次数的增多，概率接近于0，不被发现的概率很低。此外，对参与者和秘密发送方进行认证，并安全地检测通信之间的量子信道，也能识别出是假冒的。假设Bess和Charlie合作，乍看可以恢复未知量子态，事实上通过检测信道的安全性也能识别出盗窃者。

综上所述，本文所提出的两个方案均是安全可靠的。

4 结束语

本文分别基于四粒子Cluster态和五粒子Cluster态的量子信道，提出了两个n位量子态秘密共享的方案。Cluster态不同于GHZ态和W态，但是其性质却比最大纠缠态稳定，可直接用于通信。重构者Alex只需要对所持有的粒子进行相应的幺正变换即可或引入一个辅助粒子最后实施CNOT操作就可以重构原始秘密。最后通过特定的量子线路可以得到特定位量子态的秘密共享，并且只有Bess和Charlie联合才能恢复出未知量子态信息，分析表明两个方案均是安全的。且本文提出的方案在理论上成功的概率达100%。文献[4]添加辅助粒子，并对量子态进行五粒子联合测量等操作，方案繁琐，而本文只需要两次bell测量和幺正变换，步骤简单。文献[5]虽然实现了发送方和另外N-1方的秘密共享，最终只可形成n[1-(N-1)/2N-1]/6个共享秘密位。接下来将进行秘密参与者多方性的研究，完善量子秘密共享机制。