基于动态布放的潜标锚系浮力配置优化研究
2020-06-12米智楠杨群慧吴正伟
米智楠 ,程 堃 ,杨群慧 ,吴正伟 ,金 璐 ,唐 松
(1.同济大学 机械与能源工程学院,上海 201804;2.同济大学 海洋地质国家重点实验室,上海 200092;3.同济大学 国家海底科学观测系统项目办公室,上海 200092)
海洋潜标锚系是对海洋水下环境进行长期、定点、多参数剖面观测的仪器设备系统[1],具有全天候、长期无人值守、原位观测的特点,能够在恶劣的海洋环境条件下自动地对水体内部情况进行多参数剖面综合监测,为其他海洋观测手段所无法替代。国内外潜标锚系多采用单点绷紧系留方式,通过浮力保证锚系(尤其是挂载的仪器设备)的空间位置相对固定[2]。目前,对于潜标锚系的研究主要集中在锚系静态和动态力学问题、计算方法验证与实用软件编写,以及运用仿真软件进行锚系动态过程分析等方面。Chee Meng Low等[3]采用双速率时间步长方法建立了系留索动态方程;Sebastiao等[4]运用欧拉-拉格朗日方程构建系留索动态模型;Gobat等[5-6]在麻省理工学院(MIT)与伍兹霍尔海洋研究所(WHOI)的合作研究项目中,详细分析了伍兹霍尔海洋研究所设计的多种海洋锚系姿态计算问题,并编写了一套应用于实际工程的锚系姿态计算软件;Baddour等[7]对拖缆布放/回收动力学进行了研究;Ablow等[8]最早运用数值仿真方法分析海缆动力学特性;王明午等[9]建立锚系数学模型,求解了静态姿态问题;葛德宏等[10]基于集中质量法,通过MATLAB程序解算深海潜标在海流作用下的姿态;操盛文等[11]研究了一种潜标平台受到不同参数海流作用下的姿态稳定性问题;刘愉强等[12]详细分析了水动力学阻力系数,开发了对应的潜标锚系静态姿态计算软件;丁晶磊等[13]使用OrcaFlex仿真软件对单点锚泊系统进行了水动力学建模与仿真;Wang Fei等[14]对拖缆在布放/回收期间的动态响应问题进行了研究,开发了一套数值仿真程序。
国内外研究人员做了很多有意义的工作,但目前只有较少的工作考虑了实际锚系装置布放过程中的动态分析,更少有研究着重于分析浮力配置这一关键设计问题对于动态布放过程的影响,而布放过程是锚系经受的恶劣工况之一,系留索上的张力变化极大。因此,本文以对锚系动态布放过程的解算为基础,研究浮力配置方案对潜标锚系的实际影响,进而为潜标锚系的浮力设计优化提供一定参考依据。
1 水动力学分析与建模
1.1 锚系模型与坐标系说明
文中所研究的潜标锚系基本构成为:浮球、传感器仪器包、多段系留索、海床基(包括声学释放器)等,如图1所示。不同颜色节点代表不同的组成部件:黑色代表海床基节点,黄色代表浮球装置节点,蓝色代表传感器仪器包装置节点。布放采用浮球和仪器包先行投放的方案,即标锚法。作业船只以较低的恒定速度顶流航行,首先将浮球、系留索和传感器仪器包依次放入水中,浮球和传感器仪器包入水后在船尾顺列排布;当系留索基本拉成一条直线,且作业船只行驶到预定位置后,将海床基投放入水。图1中,布放初始时刻锚系为平放在海面状态,经过下沉过程之后在水平海流和浮力的作用下呈现倾斜竖立的状态。
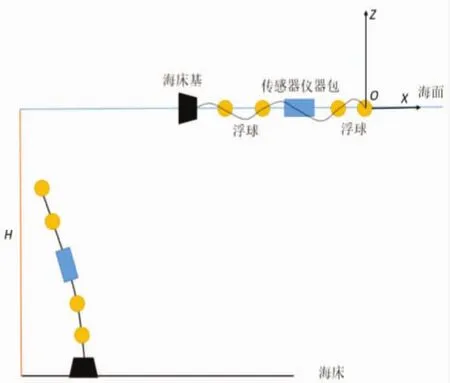
图1 锚系与坐标系示意图
潜标锚系工作水深为水下100 m,海流以平面线性流为主,采用二维坐标系进行分析和计算,所采用的流速廓线如图2所示。计算所采用的坐标系以海平面水平线为X轴,竖直方向为Z轴。原点设在顶部浮球的型心,即每个锚系模型第一个下水节点的初始坐标均为(0,0)。在水中所有节点的Z轴坐标都为负值。海流方向与X轴正向相反。
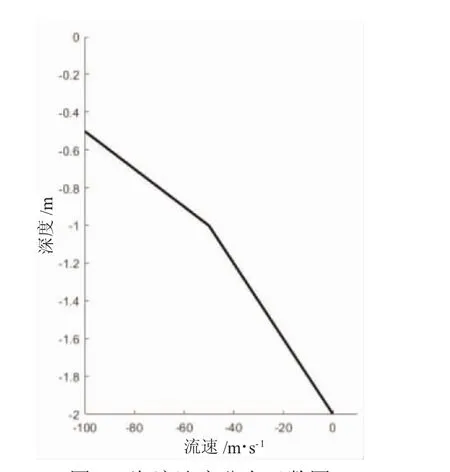
图2 海流速度分布函数图
1.2 力学分析
根据集中质量法,将系留索简化为多段忽略弯曲刚度的弹簧,系留索自身及仪器装置的质量、截面积等参数集中在系留索两端的节点,受力分析如图3所示。
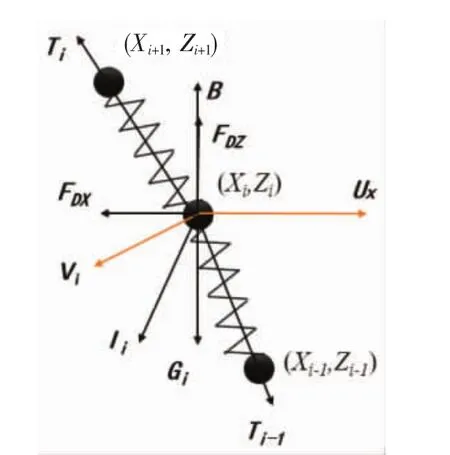
图3 节点受力分析图
在布放过程中,节点(Xi,Zi)受到的作用力包括:浮力B,重力G,系留索张力T,水动力阻力FD和惯性力I。图中,UX为海流水平流速,V为该节点的运动速度。下标i表示第i个节点。
重力、惯性力和浮力的计算分别遵循牛顿第二运动定律和阿基米德定理。
1.2.1 张力计算 系留索上张力计算遵循胡克定律,如图4所示。
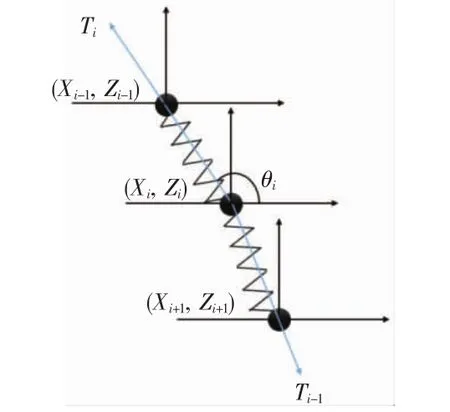
图4 张力计算示意图
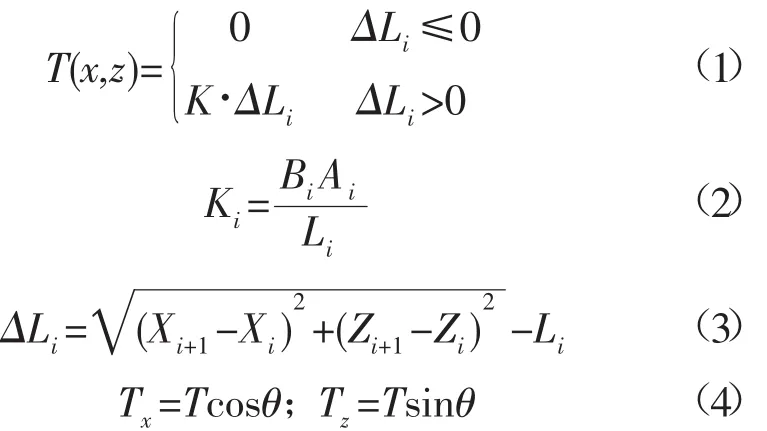
式中:Ki为弹性系数;ΔLi为第i段系留索变化长度;Li为第i段系留索原长;Ei为弹性模量;Ai为系留索截面积。
节点i所受张力为上下紧邻两绳段的绳上张力之和:
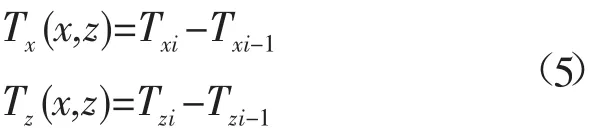
1.2.2 水动力阻力计算 水动力阻力计算方法遵循莫里森方程:

式中:ρw为流体密度;CD为流体综合阻力系数;Ai为与海流作用方向垂直的有效面积;Ui为节点i处海流速度向量;Vi为节点i的速度向量。计算中将海流假设为理想的水平流,只有水平速度。
1.2.3 海底边界条件 假定海底为泥沙地质。布放过程中,锚系的海床基在触及海床时会与之发生碰撞及摩擦,并最终会陷入海床一定深度。将泥沙质海床简化为弹簧阻尼系统模型[15]。其对节点产生的支持力FB和摩擦力fB边界条件如下:
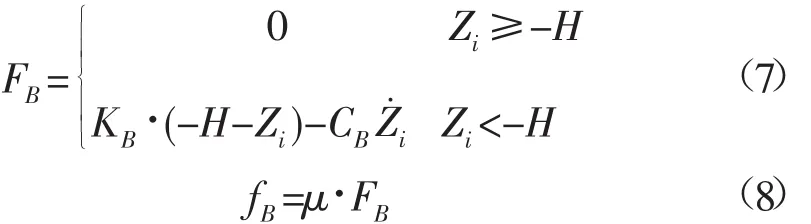
式中:KB为海床弹性系数;CB为海床阻尼系数;μ为海床摩擦力系数;H为海水深度。
1.2.4 运动控制微分方程 根据上述力学分析写出对于节点i的运动控制微分方程:
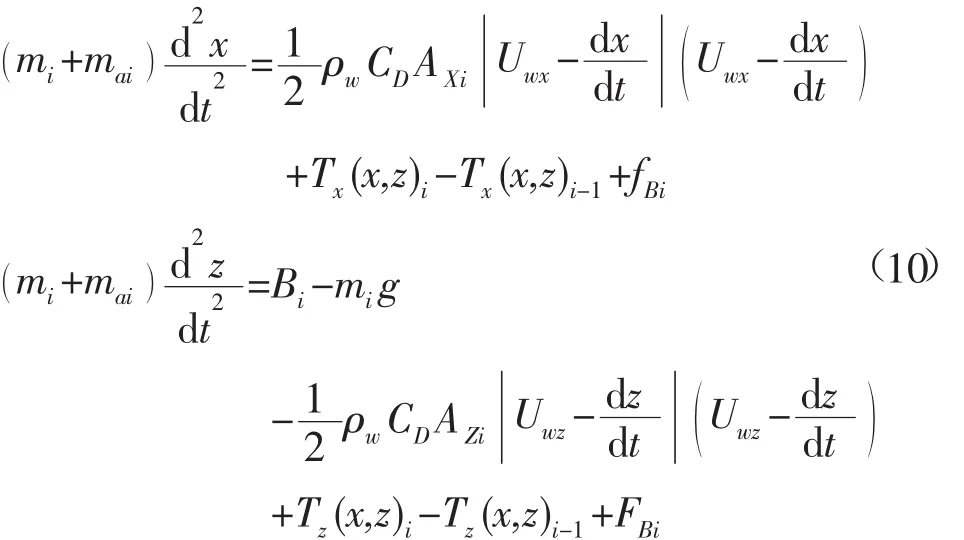
使用龙格-库塔数值方法在时间域上解算上述微分方程组,即可求得运动过程中锚系节点的位移、速度等参数。
2 不同浮力配置的结构方案
潜标锚系通过多个浮球提供浮力,所设计锚系共需28个某型号浮球提供浮力。可采用4种浮力配置的结构方案:
(1)方案1:浮球依次串联布置在整个潜标锚系的顶部。
(2)方案2:全部浮球均分为两组,一组依次串联置于潜标锚系顶部,即仪器包装置上方,另一组浮球依次串联安装在海床基上方、仪器包下方,以提高海床基回收的成功率。
(3)方案3:全部浮球均分为7组(28个浮球每4个一组,共7个紧凑浮球组),每组为一整体(通过捆绑固定等方式),依次串联布置在整个锚系顶部。
(4)方案4:全部浮球均分为7组,每组为一整体(通过捆绑固定等方式),其中4组置于潜标锚系顶部,即仪器包装置上方,另外3组布置在仪器包装置下方,即海床基上方,确保海床基的成功回收。
4种浮力配置方案的结构示意图依次如图5(a)~(d)所示。
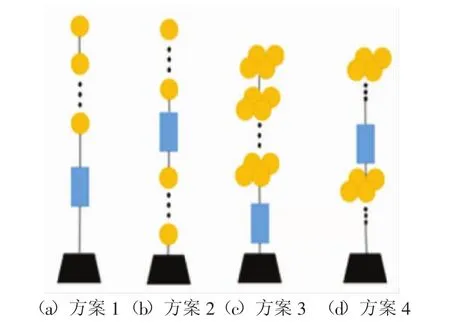
图5 浮力配置结构方案示意图
3 动态布放过程仿真与分析
3.1 节点划分
以图5中方案3的计算模型初始信息作为示例。如图6所示,将整个潜标锚系分为14个节点,1号节点为海床基节点,2~6号节点为系留索节点,7号节点为仪器包装置节点,8~14号节点为浮球节点。每相邻两个节点之间由一个系留索段连接,整个系统按照图6顺序排列共有13个缆段,后续计算将研究节点的运动参数信息和系留索段上的张力分布。
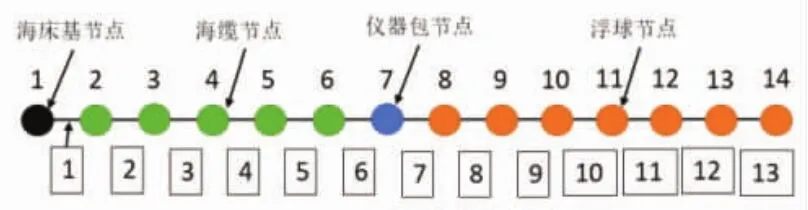
图6 方案3计算用节点划分方案
3.2 仿真参数说明
数值计算中所使用的各项力学公式系数、系留索材料参数、结构节点质量信息参数分别如表1~表3所示。

表1 各项水动力学系数

表2 系留索材料参数
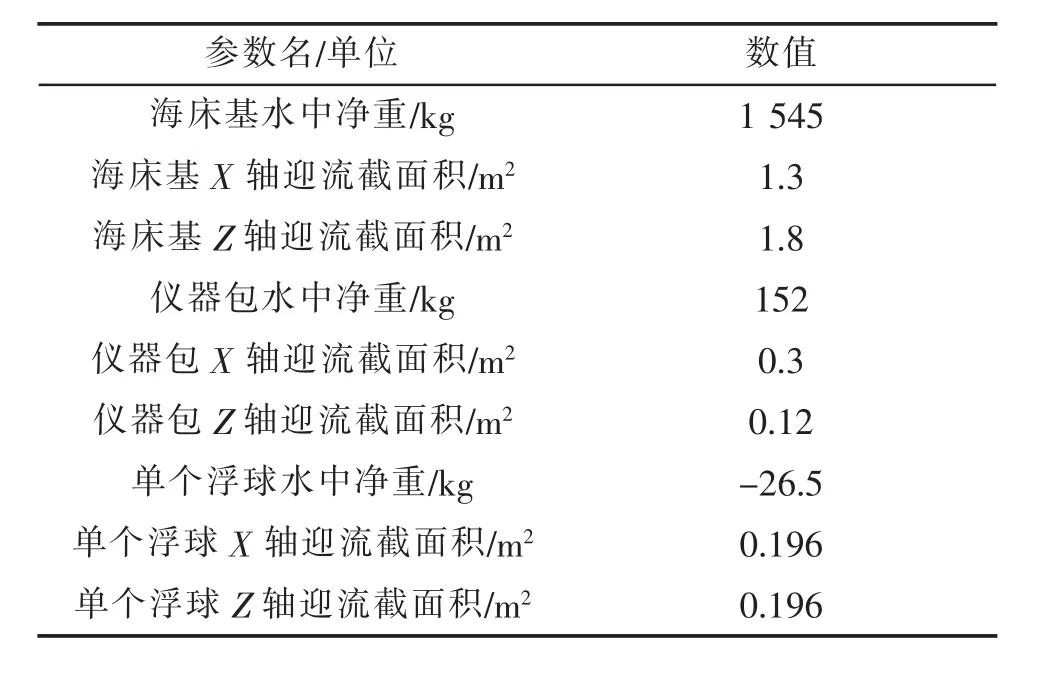
表3 各结构节点参数
3.3 姿态变化
数值计算程序模拟了从潜标锚系水平放置于海平面开始,一直到海床基着底的完整过程。经过多次计算,确定模拟时长约为80 s(方案1锚系的模拟运动难以达到稳定态,设置模拟计算时长为150 s)。通过对4种方案的垂直和水平两方向位移、运动轨迹图像进行分析和比较,以探究4种方案的各自特性。
以方案3锚系的姿态变化图说明锚系布放过程的姿态变化情况。将整个布放过程时间等分为10段,在11个时刻点上考察锚系节点位置,将各时刻点上全部锚系节点的位置连线得图7,直观表现了方案3所示锚系姿态在布放过程中的变化情况。入水时刻锚系处于水平漂浮姿态;0~16 s区间,浮球节点保持漂浮状态,海床基和仪器包节点之间的锚系逐渐下沉,本文称为布放初始阶段;24~56 s区间,整个锚系水平方向上收拢,保持近似竖直状态下沉,称为聚拢下沉阶段;64~80 s区间,海床基沉底,锚系海床基以上节点在海流的作用下漂移至稳定位置,锚系最终呈现倾斜状态,称为着底稳定阶段。

图7 方案3潜标锚系水中姿态变化示意图
3.4 垂向运动和着底过程分析
4种浮力配置方案在垂向运动和着底的仿真分析如图 8(a)~(d)依次所示。
以图8(c)为例,14条线代表14个节点的垂向位移规律。
锚系节点垂向运动规律与图7中的姿态变化过程一致。整个锚系布放过程大致经历0~16 s的布放初始阶段,浮球节点几乎不发生垂直方向位移,海床基、仪器包和EM缆逐渐下沉;16~56 s的聚拢下沉阶段,整个锚系同步下沉;56~80 s的着底稳定阶段,海床基锚定,其余各节点逐渐达到稳定态。
垂向运动分析主要对比考察海床基沉降深度和着底时间。沉降深度过大会导致海床基无法回收,影响海床基正常工作;着底所需时间越长,锚系布放安全性越低。
沉降深度方面,4种方案海床基的沉降深度几乎相同,没有明显差别。着底时间方面,方案1锚系下沉速度最快,最早着底,但海床基没有稳定,而是缓慢地被逐渐拉起,分析可知是由于大量浮球分散在浅层海流快速区域,受到海流拖曳力过大使得锚系无法锚定;方案3和方案4的着底时间较方案1和方案2更迟,分析可知是由于锚系结构紧凑,锚系更早进入到聚拢阶段,受到浮球浮力作用的时间更长。

图8 垂直方向位移图对比
3.5 水平运动分析
4种方案的潜标锚系在水平方向的运动状态如图 9(a)~(d)所示。
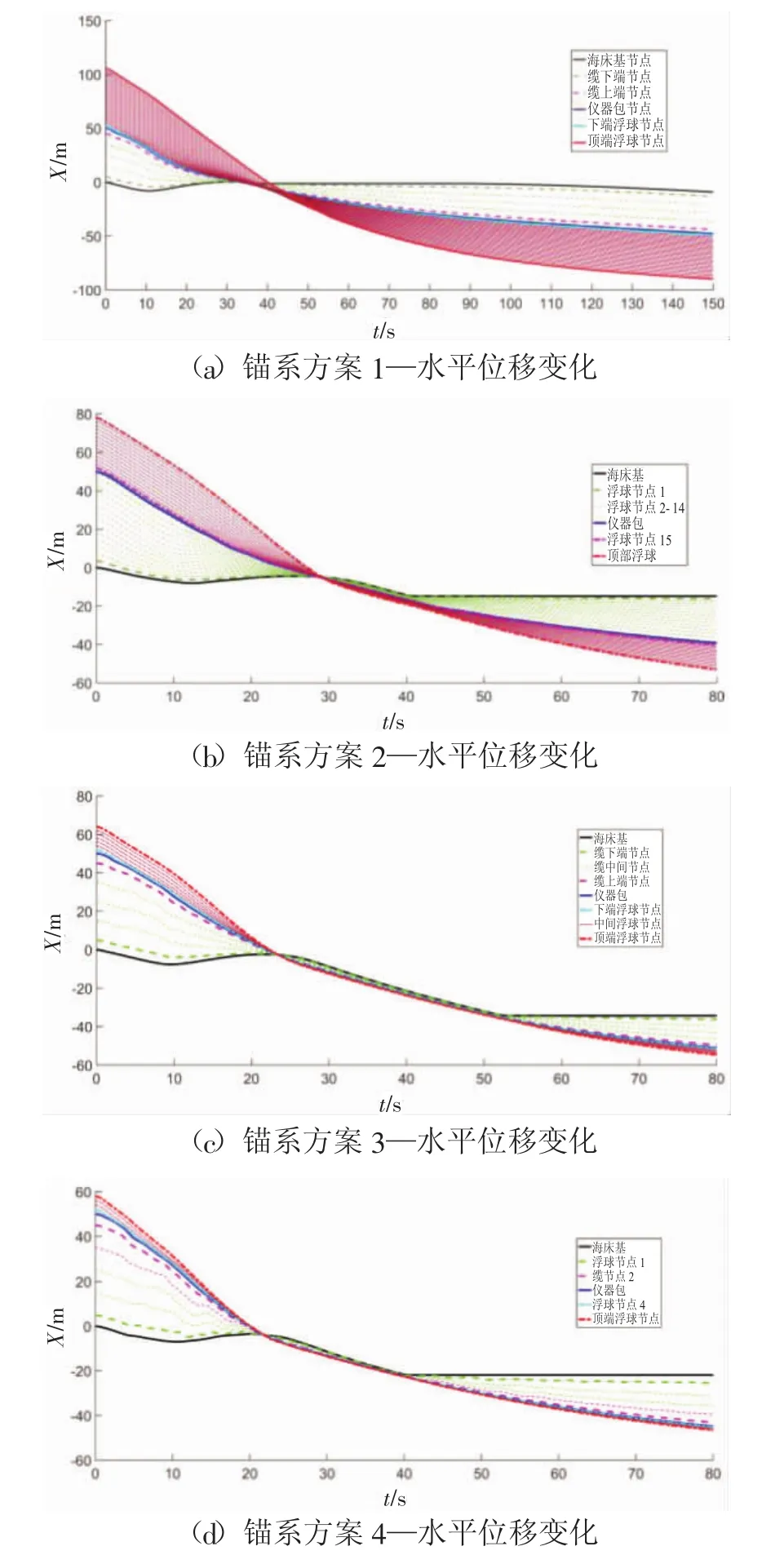
图9 水平方向位移图对比
以图9(c)为例,14条线代表14个节点的水平位移规律。整个锚系经历以下过程:0~16 s区间的布放初始阶段;16~56 s区间的聚拢漂移阶段,整个锚系被海流拖曳向X轴负方向偏移;56~80 s的着底稳定阶段,海床基锚定在海底,不再发生水平位移。
水平运动分析主要对比考察锚系海床基水平偏移距离,偏移距离越大,越难被定位回收,可能造成工程损失。
图9(a)表明方案1始终未能达到稳定平衡状态,海床基在着底后仍然被锚系缓慢拖动,产生位移。分析可知,大量浮球分布在浅层海流速度较快的区域,受到的海流拖曳力较大,导致海床基无法锚定。其余3种方案中,方案2的锚系漂移距离最小,方案3和方案4的漂移距离近似,均大于方案2。分析可知,方案3和方案4的锚系节点少而紧凑,更快进入到聚拢漂移阶段,导致更大的漂移距离。推断随着水深的增加,方案3和方案4的漂移距离将与方案2接近。
综合分析锚系节点水平位移与垂直位移的规律,可得到如下结论:锚系长度方向上设计越紧凑,则海床基在布放后越早受到浮力节点的作用,这会使整个锚系着底时间变长,漂移距离变大。若要改善这一性能指标,应适当加长上部浮球节点与下部仪器设备连接系留索的长度,使海床基等结构在布放初期能快速原位下沉。
3.6 布放过程运动轨迹分析
图10为4种锚系方案在布放中的运动轨迹。如图所示,4种锚系方案运动趋势近似,只在趋于稳态的阶段呈现出静态姿态的差别。方案1和方案2整个锚系长度更长,占据的水域也更大。方案3和方案4结构紧凑,系留索段与竖直方向夹角更小,从而可以保证传感器等设备的倾角较小,因此,方案3和方案4更能满足其对工作姿态的要求。综合可得如下结论:减少上部浮球的数量和浮力总量配置以及减小锚系长度,有利于锚系保持姿态垂直度。
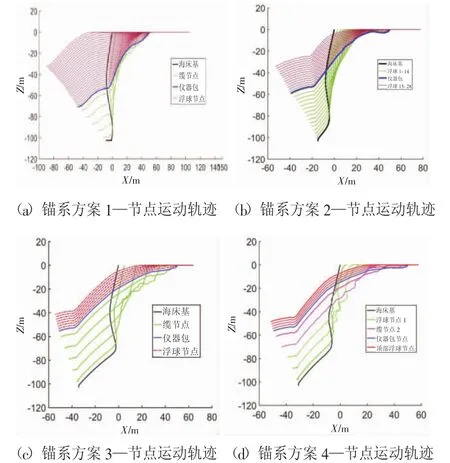
图10 锚系运动轨迹图对比
3.7 张力分布变化分析
图11 为4种浮力配置结构方案在布放过程中的张力变化图。布放过程中,系留索承受交变应力。

图11 缆段张力分布图对比
方案1和方案3的最大张力出现在仪器包上侧连接浮球节点的缆段上,而方案2和方案4的最大张力出现在海床基上侧的缆段上。根据系统结构设计方案,方案2和方案4的海床基节点与方案1和3的仪器包节点都是浮力和重力性质分界节点。由此推断,锚系中系留索最危险的部分出现在浮力节点与非浮力节点的连接段上。
在最大张力值方面,方案2和方案4的最大张力值约为1.4×104N,方案1和方案3的最大张力值约为1.6×104N。在稳态张力值方面,方案2和方案4中紧邻海床基的上侧缆段的稳态张力值约为5 000 N;方案1和方案3中紧靠仪器包的上侧缆段稳态张力值约为7 000 N。这说明,浮球分散布置(即仪器包和海床基之间布置浮球)的结构方案有助于减少缆上载荷。作为强度参考,本文研究的锚系对象采用的系留索材料为迪尼玛绳和铠装海缆,这两种材料的抗拉强度都超过了50 kN。
在缆段张力的波动振荡方面,方案1和方案3的缆段张力值振荡幅值较小,方案2和方案4的缆段张力值震荡幅值更大。这说明浮球分散布置的结构设计会导致缆段张力的震荡程度加剧。
系留索上张力值的最大值均出现在海床基着底的瞬间,海床基着底这一行为会带来剧烈的系留索张力变化。图11中方案1、方案2、方案3的着底张力变化值约为9 kN,方案4的着底张力变化值约为10 kN。
综合分析张力变化分布图,可得到如下结论:采用紧凑浮球组设计的锚系缆索动态张力指标更优;采用缆索上下部分散布置浮球方案的锚系缆索稳态张力值指标更优。设计时应根据缆索的实际工况要求,选择合适的浮力配置方案。
4 结论
通过对锚系动态布放过程中运动姿态轨迹、垂向运动、水平运动、着底时间、全程张力变化等关键项目的仿真,对比分析了4种浮力配置结构方案的力学性能指标区别和原因,提出了如下改进思路:
(1)方案3和方案4所采用的紧凑浮球组的设计方式有效缩短了锚系长度,改善了锚系的姿态垂直度,但在着底时间和水平漂移指标上表现较差。为了改善这两个指标,可在减少上部浮球节点数量(用大浮球替代多个小浮球)和浮力总量的基础上,适当加长上部浮球节点与下部非浮力节点之间的距离。
(2)浮力节点分散布置(即仪器包和海床基之间布置浮球)的方式可以有效减少缆索上的张力极值,但是会导致更大的张力变化幅度。在本研究中,由于缆段张力极值远远低于所用系留索的抗拉强度,因此方案3的设计在稳态张力值和动态张力变化方面具有较好的综合性能,能有效改善缆索的受力情况。
(3)采用以下4种锚系浮力配置方案,可有助于改善锚系布放动态性能:①减少浮力节点数量;②适当加长上部浮力节点与下部非浮力节点之间的距离;③浮力节点分散分布;④适量减少上部的浮力节点。
