深海小型履带式机器人转向动力学建模与分析

张运修，张奇峰，杨宝林,2,4，张艾群

（1.中国科学院沈阳自动化研究所 机器人学国家重点试验室,辽宁 沈阳 110016；2.中国科学院机器人与智能制造创新研究院，辽宁 沈阳 110169；3.中国科学院大学，北京 100049；4.东北大学 机械工程与自动化学院，辽宁 沈阳 110819）

海洋占据着71%的地球表面区域，蕴含着丰富的矿产、生物、天然气等资源。随着社会经济的发展和地球资源的消耗，人们愈加重视对海洋的探索和开发。当前人类已探索的海洋区域只占全部海洋的5%[1]。经过约60年的发展，海洋机器人已经成为当前人类认识海洋、开发海洋不可或缺的工具之一[2]。

海底履带式机器人因具有较强的地面行走适应性，近年来越来越多地应用于深海底部复杂环境科考、海底矿产资源开发等领域。当前，国际上研制了一系列小型化深海履带式机器人，如美国MBARI研制的Benthic Rover、德国 Wally系列、日本ABISMO遥控潜水器（Remotely Operated Vehicles，ROV）等，在深海底部的底质环境探测、生态系统和生物群落调查以及样品获取方面获取了丰富的科考成果，并根据小型履带式机器人的特点衍生出了诸多相对传统水下机器人更加经济高效的深海底部探测作业新模式[3-7]。在海底矿产资源开发方面，履带式海底采矿机器人是当前海底矿产资源开发系统中的关键装备，国际上从事深海矿产资源开发的科研机构均对该类型装备开展了研究[8-9]。

履带式机器人的行走性能是其机动性的重要组成部分，一直是人们的关注要点。对于陆地履带车辆（机器人），基于动力学分析的转向性能研究较为深入。通过建立准确的转向动力学模型，人们不仅可以分析履带式机器人转向运动学、动力学性能，还可以为机器人的结构设计和运动控制提供理论支撑[10]。早在20世纪50年代，前苏联对军用履带车辆的转向性能进行了研究，在大量简单假设的基础上，忽略了履带滑动等特性，建立了便于工程应用的计算公式[11]。然而，履带车辆在行驶过程中始终受到两侧履带打滑的影响，因此忽略滑动特性建立的转向模型的计算结果与试验结果存在较大差异。Steeds等[12-13]基于库伦摩擦准则，建立了引入打滑条件下的履带车辆转向模型，但是计算得到的履带牵引力与转向阻力矩不随车辆转向半径的变化而变化，这与履带车辆实际的测试结果不相符。Wong[14-15]在Steed的研究基础之上，基于剪切应力-剪切位移关系建立了硬质地面履带车辆稳态转向动力学模型，预测了其纵向牵引力和转向阻力矩，并进行了试验验证。Al-Milli等[17]将Wong的履带车辆转向理论延伸到软质地面，并分析了侧向阻力系数μt对履带牵引力的影响。王红岩等[18]基于履带张力对接地段压力分布影响的分析，建立了稳态转向动力学模型，并通过试验证明了该模型的准确性。欧屹等[19]基于土-履应变理论，建立了横向阻力非线性分布阻力矩模型，但缺乏仿真数据与试验数据的量化比对。

在海底履带式机器人动力学特性研究方面，日本海洋-地球科技研究所（JAMSTEC）研究人员Inoue等[20]提出将爬行式ROV的履带建模视为多个无质量的线性弹簧和有限数量的质量块组成，构建了履带数学模型，并将履带-地面接触模型简化为粘弹性模型中的开尔文模型进行模拟，建立了包含附加质量、浮力以及水动力的履带式ROV海底行走动力学方程，其仿真分析忽略了履带式ROV爬行过程中履带滑移因素的影响。韩国国家海洋研究所Lee等[21]研究了海底履带式机器人在倾斜软质地面的行驶特性，其仿真分析了浮力变化对动力学特性的影响，但未对海底履带式机器人的转向特性进行仿真分析。德国Schulte等[22]、比利时Morgan等[23]分别分析了海底履带式采矿机器人和挖沟机的牵引特性。在国内，中南大学的戴瑜、朱洪前等[24-25]基于实验室内的模拟海底土壤，开展了海底履带式机器人的压陷和剪切力学特性研究，建立了海底采矿机器人的动力学模型和履带打滑率在线实时计算模型。该模型忽略了离心力，只适合于低速运动，并且将侧向阻力系数μt设为常数，由文献[17]分析可知，该假设不符合履带车辆的实际力学特性。

本文的研究对象参见图1所示，这是一种搭载于深海多位点着陆器（M-Lander）布放下潜，并具备爬行模式的深海小型履带式机器人，本文称之为“深海漫游者机器人”（Rover ROV，下文简称RROV）。首先分析了R-ROV行走过程中履带受到的行驶阻力，并进行了水动力分析仿真，得到了行驶水阻力；然后基于剪位移-剪应力的关系，建立了针对R-ROV的稳态转向动力学模型，并将离心力、履带的滑移特性因素考虑在内，通过迭代求解得到海底履带式机器人运动参数的数值解；最后基于RecurDyn动力学仿真软件构建了R-ROV动力学仿真模型，通过对比海底底质环境下的行走动力学仿真分析数据与理论计算结果，验证了理论分析的正确性，由此可为海底履带式机器人的结构设计和行走控制提供理论支撑。

图1 爬行模式下的深海漫游者机器人

1 R-ROV海底行驶阻力计算

1.1 履带行驶阻力

海底履带式机器人在海底松软沉积物上行驶，无法避免地产生沉陷，进而产生较大的压实阻力和推土阻力。然而，海底底质环境复杂，土壤参数复杂多变并难以获取，本文采用文献[16]中的经验公式估算阻力系数μr：

式中：CI为圆锥阻力系数，则履带的行驶阻力为：

1.2 水阻力

R-ROV海底行驶时，由于水流的影响，会产生水阻力。R-ROV海底实际运动时转向角速度较低，因此本文只考虑转向过程中的直航阻力进行分析。本文基于STAR-CMM+仿真软件进行R-ROV水动力仿真分析。仿真分析过程为：首先通过简化机器人模型（见图2（a））进行网格划分，采用平均雷诺数基础上的N-S方程分析预测机器人周围流场；之后选定湍流模型为标准K-ω模型；最后通过设定合理的边界条件，得到了R-ROV前进方向在不同来流速度下受到水阻力值，仿真得到的速度云图如图2（b）所示。表1为不同速度下仿真得到的水阻力大小。

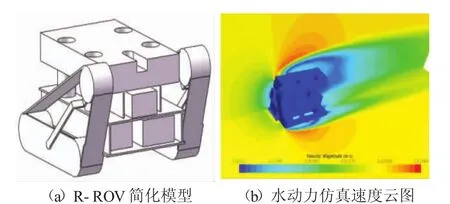
图2 R-ROV水动力仿真

表1 R-ROV不同来流速度下的直航水阻力变化表

2 海底土壤条件下的R-ROV稳态转向动力学建模

本文基于Wong[14]提出的硬质路面下履带车辆稳态滑动转向理论，分析海底履带式机器人在特定软质海底场景下的转向运动情况，并开展R-ROV海底爬行仿真分析研究。R-ROV设计深度为3 000 m，由模块化底盘和浮游体两大部分组成。底盘和浮游体机械固定后，R-ROV基于两条履带在海底进行爬行运动，通过分别控制左右履带的电驱动关节实现R-ROV的转向运动。R-ROV样机的机械参数如表2所示。

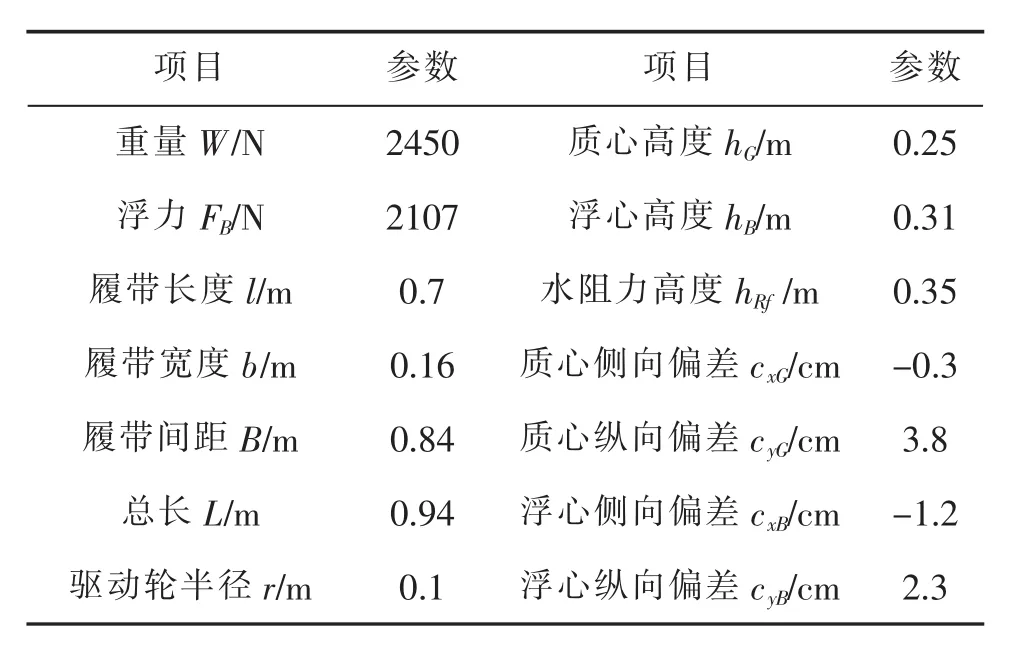
表2 R-ROV主要设计参数

2.1 坐标系统描述

为分析海底履带式机器人的运动特性，建立如图3所示坐标系，OXY为大地坐标系。设定坐标系o1x1y1固连在机器人转向运动外侧履带中心线上，坐标系原点o1与重心CG的距离为机器人转向中心的纵向偏移量为s0。同理，设定转向内侧履带坐标系o0x2y2。cxG，cyG与cxB，cyB分别表示重心、浮心相对 RROV形心的横向和纵向偏移量。当机器人在海底以角速度φ˙围绕旋转中心O点运动时，外侧履带纵向绝对速度可以表示为：

式中：R'=R·cosβ

海底履带式机器人在稳态转向过程中，设定以下条件：

（1）忽略履带支重轮对接地压力的影响，履带与地面的接地压力成连续线性分布；

（2）机器人在运动过程中，履带不发生拉伸变形；

（3）履带稳态转向过程中，履带-地面接触点受到的剪应力取决于该点的剪切位移；

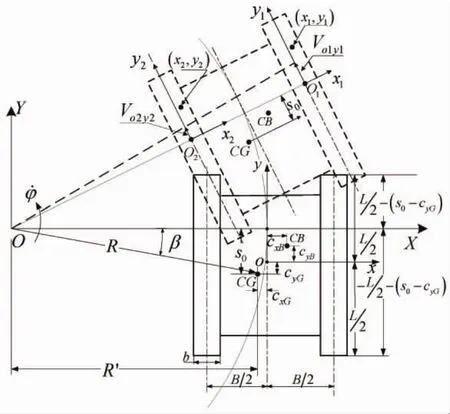
图3 坐标系及转向运动学关系

（4）忽略履带的履刺效应对牵引力的影响，履带纵向阻力系数在行驶过程中不发生变化。

2.2 R-ROV运动学模型

将R-ROV的运动模型简化为二维，如图3所示，设定其自身坐标系为oxy，原点设置在形心。设R-ROV在地面行驶过程中内外侧履带的打滑率分别为ii，io，则内外侧履带相对地面的实际速度为：

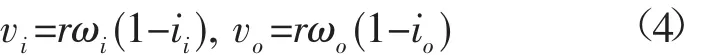
在考虑履带打滑的情况下，可得到R-ROV转向运动时的前进速度和转弯半径：

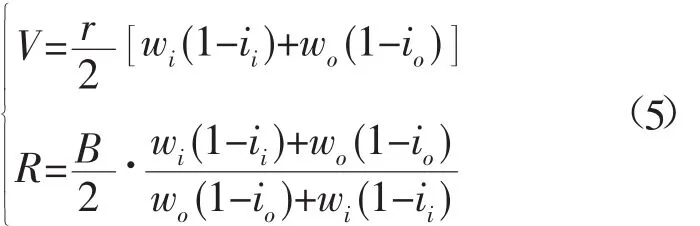
2.3 接地压力计算

海底履带式机器人在转向过程中，由于离心力的存在，机器人的转向中心会发生纵向偏移，进而引起两侧履带接地压力的变化。假设履带压力分布呈梯形分布，同时为便于计算，将水阻力Rf简化成一个集中力，得到如图4所示的R-ROV接地压力分布示意图。

根据力平衡和力矩平衡关系得到外侧履带接地段的法向负荷：

图4 R-ROV接地压力示意图

基于坐标系平移和力平衡、力矩平衡条件，得到两侧履带接地应力公式：

2.4 海底软质地面下的履带稳态转向受力分析

2.4.1 履带与地面的剪切变形计算 图5是海底履带式机器人稳态转向时内外侧履带受力情况。

图5 稳态转向时两侧履带的受力分析

根据Wong[14]提出的履带剪切位移理论，在大地固定坐标系OXY下，转向时的外侧与内侧履带任意一接地点（x1,2，y1,2）的X-方向剪切位移jXo,i和Y-方向剪切位移jYo,i可分别表示为：

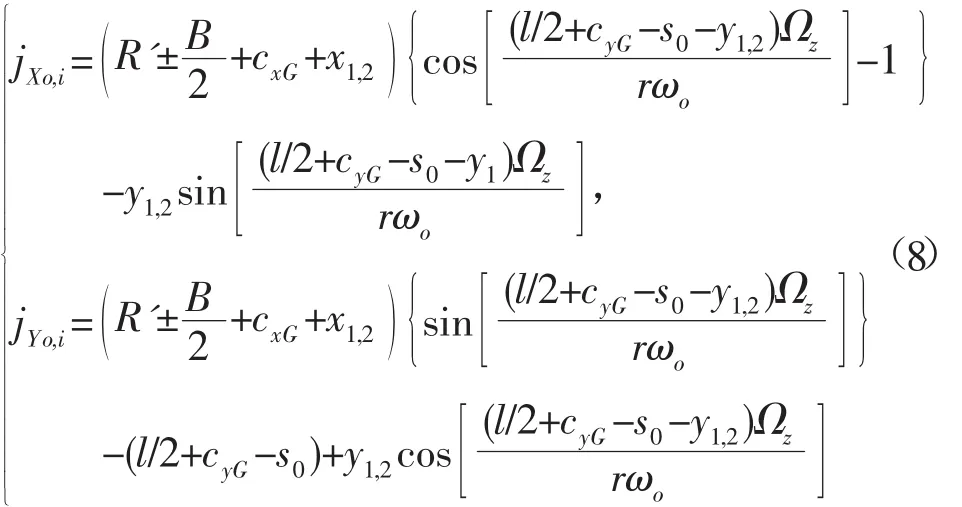
式中：Ωz为海底履带式机器人围绕转向中心点O的偏航角速度。根据式（7）可推出履带接地段任意点（x1,2，y1,2）的剪切位移：

2.4.2 履带剪切力与转向力矩 Wong[14]提出的剪切应力-剪切位移关系适用于硬质地面土壤环境，根据文献[17]分析：剪切位移-履带在软质土壤条件下的接地段剪应力与剪切位移满足关系式：

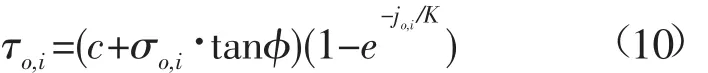
式中：c为土壤内聚力；φ为土壤内摩擦角；K为土壤剪切模量。

因此，图5中的履带接地段单位面积dA上的剪切力dFo和dFi可以用下面的公式得到：

计算履带与地面之间的剪切作用力的横向分量Fxo，Fxi和纵向分量Fyo，Fyi：

式中：δ1,2代表了转向外侧和内侧履带滑动速度与x轴的夹角，可根据Wong[14]提出的公式计算：

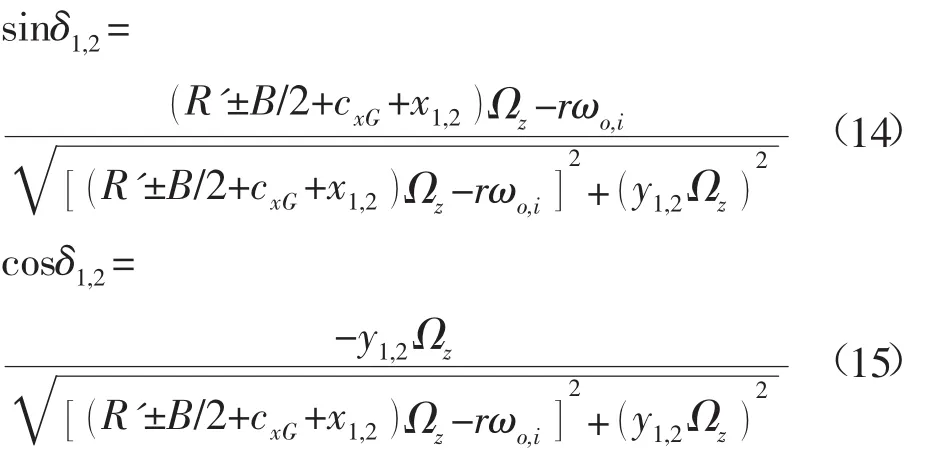
R-ROV转向时的内外侧履带纵向剪切力将产生相对于图5中OV点的转向驱动力矩MLo和MLi：

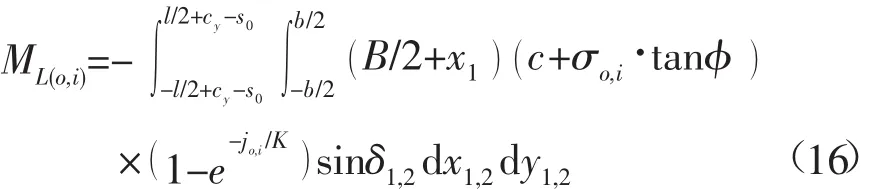
与此同时，履带剪切力的横向分项将使内外侧履带分别产生相对图5中O1，O2点的转向阻力矩Mro和Mri：

2.4.3 稳态转向动力学方程 通过对R-ROV的转向运动机理分析，可以得到R-ROV在稳态转向运动时的动力学方程：

3 转向过程仿真与试验验证

3.1 稳态转向动力学求解方法

转向动力学方程式（18）～式（20）中，当给定RROV结构参数与土壤参数之后，只有3个未知变量需计算：履带驱动轮转速ωo，ωi和转向中心的纵向偏移量s0。基于Matlab中非线性方程组求解工具箱，可迭代求出上述3个变量的最优值，迭代求解流程如图6所示。将迭代求解得到的驱动轮转速wi，wo最优解以及半径R、转速V设定值代入式（5）中可求出内外侧履带的滑转率。

3.2 履带牵引力、滑转率及转向阻力矩的仿真分析

海底土壤的参数复杂多变，无法找到可以直接应用的海底土壤参数，这里参考文献[24，26-27]给出R-ROV海底爬行区域的土壤参数设定值。

表3 海底土壤参数

图6 R-ROV稳态转向动力学方程组迭代求解流程

将表2中爬行模式下R-ROV的结构参数、表3中的土壤参数代入稳态转向动力学方程，按照图6的流程进行迭代计算，求解位置变量，得出R-ROV不同爬行条件下的履带滑转率、转向阻力矩以及纵向牵引力。

针对左右驱动，履带动力学方程可简化为[28]：

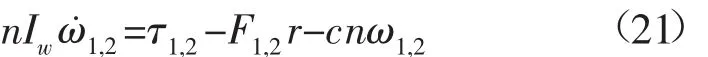
式中：Iw为履带驱动轮的转动惯量；τ为电机关节产生的转矩；c为综合阻尼系数，取c=0.35；减速比n=100。履带牵引力F1,2为理论计算得到的纵向牵引力。从式（21）可以看出，在稳态运动状态下，履带牵引力的变化与关节驱动力可以认为是线性关系，但实际关节驱动力矩受多个外部因素影响，所以本文给出理论计算得到的履带牵引力特性，关节驱动力矩在动力学仿真和样机试验中给出对比。

计算得到的R-ROV两侧履带牵引力如图7所示，两侧履带牵引力都是随转向半径的增大而变小。在半径较小时，由于高速侧履带牵引力是主动产生，低速侧履带与地面的剪切力是由车体拖动履带与地面之间的滑动产生，因此两者方向相反。图7与文献[10]中描述的陆地履带车辆不同的是，虽然R-ROV的离心力起到有利于转向的作用，但是履带牵引力并没有随着速度的增加而变小，这主要是因为在水中行驶速度增加，会导致水阻力变大，与离心力相比，水阻力增加变成了主要影响因素。

图7 R-ROV不同速度时内外侧履带纵向牵引力随转向半径变化的关系曲线

图8 给出了内外侧履带滑转率随速度、转向半径变化的关系。图中，R-ROV两侧的履带滑转率都随着转向半径的增大而减小；两侧履带的滑转率在转弯半径低于3 m时，滑转率较大并且变化明显；对于高速侧履带，转向速度的增加导致滑转率升高；对于低速侧履带，当转向半径小于10 m时，速度的提升会导致换转率降低变得明显，转向半径大于10 m时，转向速度对滑转率的影响较小。

图8 R-ROV不同速度时的履带滑转率随转向半径变化的关系曲线

图9 为海底环境下，R-ROV转向阻力矩随转向速度、转向半径的计算结果。从图中可以看出，转向阻力矩随着转向半径增加而减小，转向速度对履带的转向阻力矩影响较小。

3.3 基于RecurDyn的动力学仿真试验验证

为验证理论分析得到的转向动力学模型的准确性，本文基于RecurDyn仿真软件进行了动力学仿真。图10为在RecurDyn中的仿真流程：在RecurDyn仿真软件中构建履带-摆臂模块，设置地面土壤环境参数；将R-ROV的三维模型进行简化，分模块保留其机械属性，之后将R-ROV的三维模块导入RecurDyn中；添加浮力、水阻力，为便于进行动力学仿真，R-ROV的水中浮力、水阻力以集中力的方式添加；设定高速侧、低速侧驱动轮转速作为仿真输入；设定仿真时间、取样周期，运行仿真。构建的RecurDyn仿真模型和动态轨迹如图11所示。

图9 R-ROV不同速度时的履带阻力矩随转向半径变化的关系曲线

图10 基于RecurDyn的R-ROV动力学仿真流程

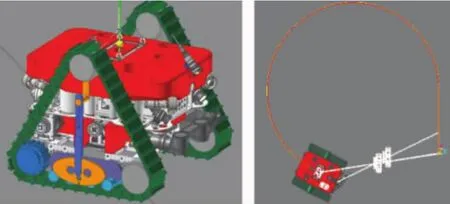
图11 RecurDyn中构建的R-ROV模型与仿真效果

为验证R-ROV的稳态转向性能，取3.2章节旋转半径1～20 m中的奇数组，计算得到的驱动轮转速理论计算值作为RecurDyn仿真软件中RROV两侧履带驱动轮转速设定值。设定的土壤参数采用表3中数据。运行RecurDyn仿真得到R-ROV的稳态平均速度与旋转半径结果，如表4所示。

表4中，R为理论转向半径；ωi/ωo为理论计算得到的内外侧履带驱动轮转速；VR与RR分别为RecurDyn仿真得到R-ROV前进速度与转向半径。

分析表4中数据可得：RecurDyn中得到的RROV稳态转向半径R、前进速度V与理论计算值结果误差在10%以内，证明了基于履带剪切位移-应力推导的R-ROV稳态转向动力学方程是合理的。

如图12所示，R-ROV在运动的初始阶段并没有按照既定半径进行运动，而是运动轨迹半径逐渐缩小，这是由于在初始阶段，履带加速过程与稳态过程产生的滑转率区别较大，使R-ROV的运动轨迹产生改变，后期R-ROV运动半径逐渐收敛至期望半径。上述现象表明，期望R-ROV海底行驶特定轨迹需要动态的控制策略调整驱动轮转速。

表4 设定转向速度V=0.4 m/s时的RecurDyn仿真输入及输出数据

图12 仿真R=5 m时得到的R-ROV运动轨迹曲线

3.4 水池条件下R-ROV动力学仿真数据验证

水池条件下，利用R-ROV样机进行了动力学仿真数据对比研究，图13为R-ROV进行水池试验的场景。水池试验流程：首先，R-ROV搭载于深海多位点着陆器（M-Lander），组成联合探测系统共同布放至20 m深水池底部；之后，水面遥控R-ROV爬行出坞，使用履带进行水池底部运动性能试验；最后，遥控R-ROV返回M-Lander坞内进行回收。

R-ROV借助M-Lander与水面的通信回路下达指令至R-ROV，并将底盘关节的数据定时回传。通过收集底盘关节驱动电机的电流和关节转速，可获取R-ROV履带驱动轮的驱动转矩和R-ROV的前进速度。

实际试验时，R-ROV的履带速度V约为0.35～0.5 m/s。通过本次试验得到的履带速度和驱动关节实际驱动力矩如图14所示。同时为对比分析，在RecurDyn中仿真R-ROV直行速度V=0.4 m/s得到的关节驱动力矩如图15所示。

图13 R-ROV在20 m深水池底部试验场景

图14 R-ROV水池底部设定V=0.4 m/s爬行时的履带驱动轮关节转矩曲线

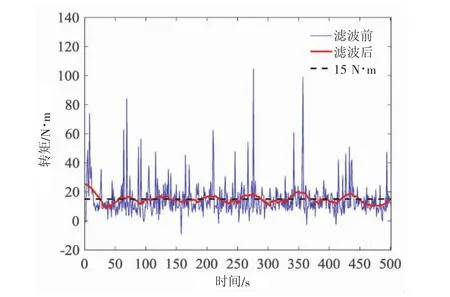
图15 RecurDyn中V=0.4 m/s时的关节驱动力矩

图16 为R-ROV在水池底部做原地转向运动时得到的履带驱动关节转矩与RecurDyn仿真数据对比结果。从图中可以看出，仿真与水池测试得到的高速侧、低速侧履带驱动关节转矩较为吻合：外侧关节平均转矩分别为28.61 N·m与27.74 N·m，内侧履带驱动关节平均转矩为-21.25 N·m与-20.34 N·m，仿真与实际误差均在10%以内。内侧关节转矩绝对值要小于外侧转矩，这是由于在较小半径范围内，离心力对低速侧履带牵引力的影响更明显[10]。

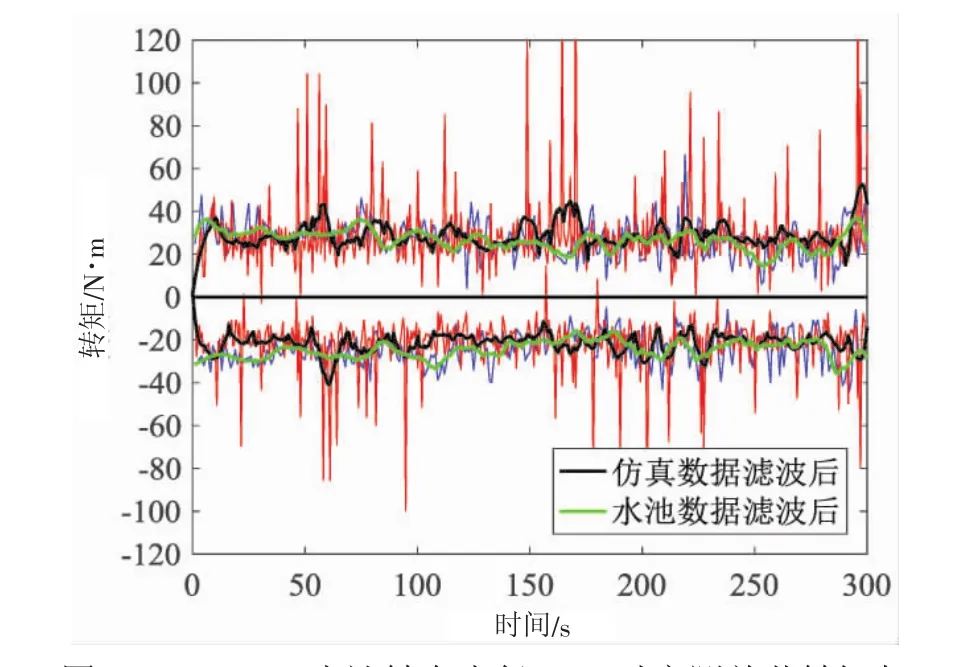
图16 R-ROV水池转向半径R=0时实测关节转矩与RecurDyn仿真得到关节转矩数据对比

4 结论

（1）本文对一款可在海底爬行的履带式机器人（R-ROV）开展了转向动力学建模与分析，构建了稳态转向动力学方程。通过针对R-ROV开展水动力仿真分析，得到了10组不同速度下的水阻力数据。针对工程化应用构建的简化动力学与真实环境不相符的问题，基于履带的剪位移与剪应力之间关系，构建了R-ROV的稳态转向动力学方程组，并将履带滑转、浮力与水动力参数考虑在内。

（2）仿真分析了运动性能的影响因素。通过非线性方程组迭代求解，得到了机器人爬行过程中的未知变量最优解：内外侧驱动轮转速ωi，ωo以及转向中心的纵向偏移量s0，之后将数值代入方程，分别求得履带滑转率、转向阻力矩、履带牵引力与转向半径R、前进速度V之间的关系；通过对土壤的参数设定，得到了R-ROV的海底运动适应性预报，该仿真分析对R-ROV工程化设计和实际海上应用提供了理论依据。

（3）利用动力学仿真软件RecurDyn进行了仿真验证。通过简化R-ROV的三维模型、构建RecurDyn下的R-ROV的模块化履带模型，开展了R-ROV在RecurDyn软件中不同土壤工况下的动力学仿真，仿真结果与理论计算差值在20%以内。仿真试验说明R-ROV的运动轨迹受土壤条件和自身运动情况影响，控制期望轨迹路线需要添加闭环控制策略。

（4）开展了R-ROV样机的水池行走试验研究。研究结果表明，R-ROV具备水中爬行的能力，得到了水池硬质地面行驶关节转矩，与基于RecurDyn的动力学仿真基本吻合，证明了动力学仿真分析的正确性。后期将开展真实海底环境下的行驶性能研究，进一步验证理论分析结果。