基于北斗的地基增强系统多基准一致性检验算法

胡 杰, 严勇杰, 石潇竹

(1.中国电子科技集团公司第二十八研究所, 南京, 210007；2.空中交通管理系统与技术国家重点实验室, 南京, 210007)

全球导航卫星系统(Global Navigation Satellite System, GNSS)现已逐步完善，它凭借全球、全天候、高精度等优点受到越来越多的应用[1]。国际民航组织计划利用卫星导航系统替代传统地面导航设备，降低航空导航成本，增加航路设计[2-3]。地基增强系统(Ground Based Augmentation System, GBAS)在采用差分技术提高卫星信号测距精度的基础上，增加一系列完好性监测算法，提高了导航系统的完好性和可用性[4-5]。随着我国北斗卫星导航系统(Beidou Navigation System, BDS)在民航领域中的应用范围越来越广泛[6]，国内科研院所正在积极开展基于BDS的GBAS差分定位与完好性监测等研究工作，如中电54所、28所等围绕卫星信号完好性监测[7]、机载差分定位[8]等开展研究，北京航空航天大学王志鹏[9]、薛瑞[10]等人一直致力于基于双频多星座的III类精密进近与着陆卫星导航关键技术研究，对我国BDS在民用航空导航中的应用具有积极的引导作用。

Stanford大学给出了GBAS地面系统完好性监视平台仿真模型，包括信号质量监测、数据质量监测以及观测质量监测等，并计算通过一系列完好性监视后的卫星信号伪距差分校正值[11]。为了确保多个基准站计算得到的差分校正具有一致性，需要在广播差分校正值前进行多基准一致性检验(Multiple Reference Consistency Check, MRCC)，以隔离可能存在故障的接收机。RTCA DO245[12]标准中给出了一种基于极大似然估计准则的MRCC算法，该算法通过比较各个基准站的差分校正值并计算其B值以判别基准站接收机是否存在故障。Dautermann[13]将该方法应用于德国DLR机构研制的GBAS地面系统中心处理单元中，并指出可以根据B值的标准差评估GBAS地面系统精度，但是对于B值门限值的设定方法并未提及。李亮[14]、徐轲[15]指出由于各个基准站之间存在相关性，基于极大似然估计准则的MRCC算法无法有效区分故障来源，因此提出了一种基于Kalman滤波的B值计算新方法，该方法是建立在假设某一基准站接收机发生故障的概率为零的基础之上，在实际中该假设一般难以成立。胡杰[16]、刘军[17]等人针对传统MRCC算法无法检测故障卫星的问题，提出了一种GBAS中基于导航监测的B值修正算法，由分析可知，地面系统经过一系列完好性监测后，已经将卫星故障予以排除，但该算法存在冗余，并没有有效解决B值相关性问题。

针对上述问题，本文提出了一种基于高斯膨胀法的B值门限值计算方法，并利用实验室研制的GBAS原型系统进行了验证实验。

1 基于极大似然估计准则的MRCC算法

假设GBAS地面系统有M个基准站，经过一系列完好性监测后可用卫星个数为N。基准站精确位置信息已知，利用已知点位置与卫星空间坐标可以计算得到第j颗卫星与第i个基准站之间距离为R(i,j)，进一步与经载波相位平滑后的伪距进行差分可以得到平滑伪距的差分校正值为：

PRSC(i,j)=PRS(i,j)-R(i,j)+τ(i,j)

(1)

式中：i为第i个基准站；j为第j颗卫星；PRS为经载波相位平滑后的伪距观测值；R为星站之间真实距离；为卫星钟差校正值。

由式(1)计算得到的差分校正值中包含接收机钟差，因此需要进一步消除该项误差。对于第i个基准站而言，其所有可观测卫星的接收机钟差大小相同，因此可以利用差分校正值估计该接收机钟差，进一步可得：

(2)

(3)

式中：PRSCA为补偿接收机钟差后差分校正值；PRCORR为地面系统最终播发的差分校正值；c(j)为基准站接收机与机载接收机之间关于第j颗卫星的公共伪距误差；Sc为可用卫星集合;Si为可用基准站集合。

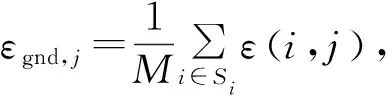
(4)

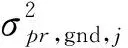
GBAS中心处理单元广播差分校正值前必须确保所有基准站计算的校正值具有一致性，因此需要对多个基准站的一致性进行检验。文献[12]中给出了GBASB值计算方法，同时规定只要任意一基准站的B值超过设定门限值则需排除该通道，B值计算公式为：

(5)

式中：BPR(i,j)表示第i个基准站所观测到的第j颗卫星的B值。

进一步可以利用B值的标准差σB对GBAS地面系统精度进行评估，其关系可表示为：

(6)

式中：σB为地面系统计算得B值的标准差，σpr, gnd、PRCOOR以及B值最终通过VDB电台广播给机载用户，以实时计算飞机位置和保护级。

2 GBAS B值理论分析

GBAS地面系统中MRCC算法主要用于检测地面基准站生成的伪距差分校正值是否具有一致性，通过计算各个基准站对应可见卫星的B值，以隔离其中不具备一致性的差分量。

令Yij=PRsc(i,j)，其中，i=1,2,...,M，j=1,2,...,N，假设M=4，N=4，则总观测量个数为16，如表1所示，Y·j/M、Yi·/N、Y../MN分别表示列均值、行均值以及总均值。

表1 平滑伪距的差分校正值列表形式

Zij=PRSCA(i,j)=Yij-Yi·/N

(7)

由式(7)以及表1定义可得：

Z·j=Y·j-Y··/N

(8)

将式(2)、式(7)和式(8)带入式(5)可得：

(9)

假设Yij的均值为μ;αi表示第i个基准站接收机误差;βj表示第j颗卫星误差，则Yij可表示为：

Yij=μ+αi+βj

(10)

当M=4，N=4时，式(10)可写成如下方程形式：

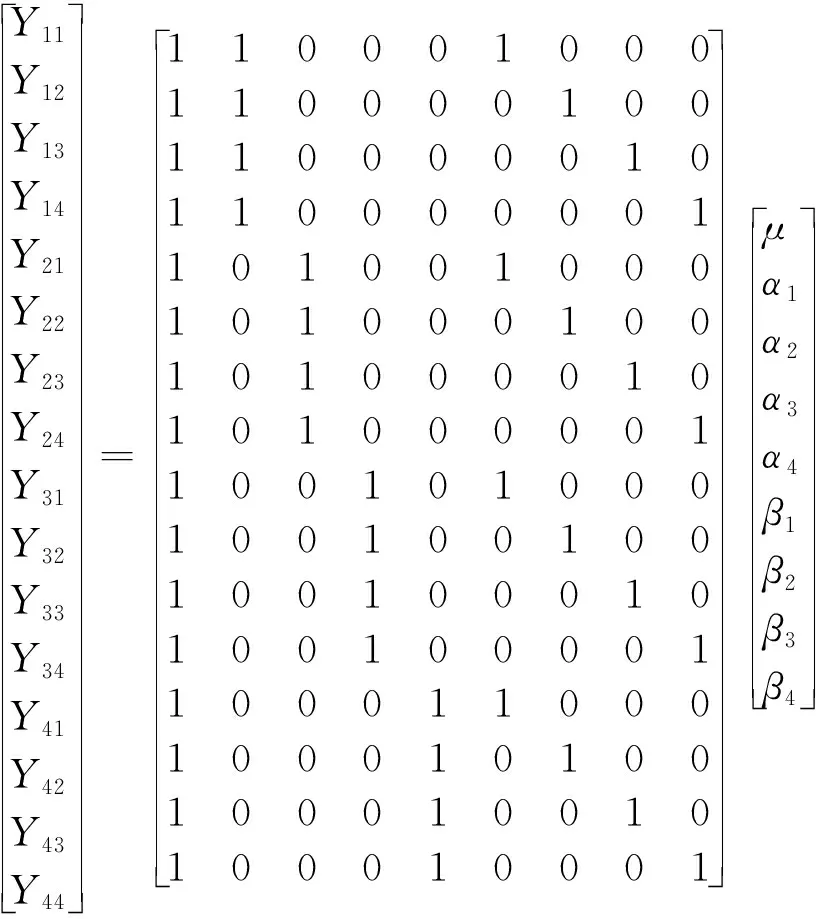
(11)

将式(11)写成矩阵形式，即：

Y=GX

(12)

利用最小二乘法可以得到变量X的估计值为：

(13)

进一步根据GBAS线性模型最小二乘估计方法可得[18]：

(14)

将式(14)带入式(9)，B值可表示为：

(15)

由式(15)可以看出，B值的大小体现了基准站接收机故障以及卫星故障引起的伪距差分校正值的偏差多少。当基准站接收机和卫星无故障时，B值是伪距差分校正值与其均值的偏差，其数值在较小的范围内变化，一旦出现任何故障，B值将会大幅跳变，因此通过设定的门限值能够将故障予以检测。

传统基于B值的处理算法无法区分故障来源，针对该问题本文给出了一种能够区分故障来源的MRCC算法处理流程，如图1所示。假设地面基准站个数为4，由图1可以看出，地面系统经过一系列完好性监测后形成可用卫星集合，当可用卫星个数小于4颗时，地面系统告警，表示此时GBAS不可用。当可用卫星个数大于4颗时，则分别计算每颗卫星对应4个基准站的B值，并与设定的门限值进行比较，如果B值在门限值范围以内，说明通过一致性检验，否则需要将其中最大B值对应的基准站予以移除，然后计算剩余基准站对应可见卫星的B值，并进行判别，如果B值不超过门限值，则说明剩余3个基准站通过一致性检验，否则说明地面系统可用基准站个数小于3，不满足系统完好性需求并告警。

图1 MRCC算法流程

3 基于高斯膨胀法的门限值计算方法

为了判别B值是否异常，需要确定适合的门限值，本文提出一种基于高斯膨胀法的检测门限值计算方法，具体实现过程如下：

步骤1根据GBAS地面系统4个基准站处理得到的伪距差分校正值计算B值，并进行预处理，确保所得样本数据具有较好的一致性。

步骤2以10°为区间划分步骤1中所计算得B值，并分别计算其均值μ(θ)和标准差σ(θ)，θ表示相应卫星仰角大小。

步骤3利用多项式拟合卫星仰角区间0°～90°内其他角度均值及标准差。

步骤4利用步骤3中拟合得到的B值均值和标准差对样本数据进行归一化，具体计算如下：

(16)

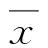
步骤5绘制归一化后B值的分布直方图，并计算各个样本区间概率密度值。

步骤6根据步骤5中计算得概率密度值绘制概率密度分布曲线，并在图中加载均值为0，标准差为1的标准正态分布曲线，然后对标准正态分布曲线进行膨胀，直至膨胀曲线包络样本数据概率密度曲线两侧，由此可得膨胀系数。

确定好膨胀系数后，根据卫星仰角可以得到对应角度下B值的均值和标准差，由式(17)可以得到B值门限值为：

Threshold(θ)=μ(θ)±Kffd·f·σ(θ)

(17)

式中：μ(θ)、σ(θ)分别表示卫星仰角为θ时地面系统B值的均值和标准差;Kffd为乘数因子;为满足I类精密进近导航完好性需求，取值为6;f为计算得膨胀系数[19]。

利用实验室GBAS平台采集一组BDS卫星数据，实验时间为2019年5月17日8∶00至2019年5月18日8∶00，总时长为24 h，按步骤1～6计算得到膨胀系数，图2为归一化后的B值概率密度分布曲线，其中蓝色点线为实际过程数据的概率分布，紫色实线为标准高斯正态分布概率密度曲线，红色点画线为经过高斯膨胀后的概率密度曲线，由图2可得对应的膨胀系数f=1.251。

图2 归一化B值概率密度曲线

4 验证实验

4.1 实验环境

文中实验室于2017年初研制了GBAS原型样机，可实时监测BDS/GPS卫星状态。GBAS地面系统包括：4个基准站及相应卫星接收天线、中心处理单元以及VDB发射电台等，软件部分主要包括以下4个进程，如图3所示。

图3 中心处理单元模块

4.2 实验结果分析

GBAS地面系统4个基准站接收卫星信号，并分别计算每个基准站对应可观测卫星的PRSCA和B值，图4和图5分别为2019年6月1日4个基准站对应6号卫星的PRSCA和B值及其门限值曲线，图6为利用B值计算得地面系统校正值误差标准差随卫星仰角变化曲线，图中红色实线为根据RTCA DO245计算得GBAS地面系统精度等级，说明实验室研制的GBAS原型样机具备A级精度。

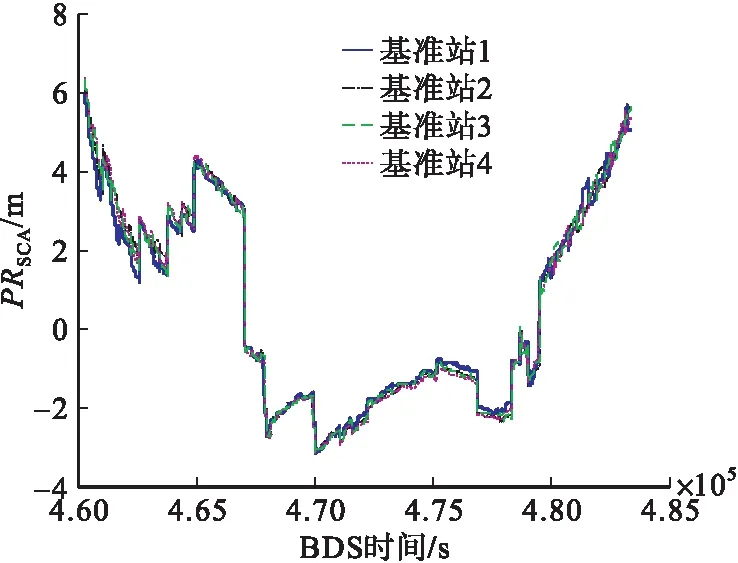
图4 6号卫星对应4个基准站伪距差分校正值

图5 6号卫星对应4个基准站的B值及其门限值

由图4～5可以看出，6号卫星在该时间段内的PRSCA具有较好的一致性，因此其B值没有超出设定的门限值，通过一致性检验，进一步对4个基准站伪距差分校正值进行平均可以得到该时间段内6号卫星所播发的PRCORR。由图6可以看出，随着卫星仰角变大，伪距所受多路径以及电离层干扰影响逐渐变小，因此对应的差分校正值误差的标准差也逐渐变小，数据结果与理论分析一致。

为进一步对本文提出的多基准一致性检验算法进行验证，将基准站1对应的接收机伪距观测值在历元10 000至12 000之间(对应的BDS周内时间为470 288～472 288 s)注入5 m测量误差，以此模拟基准站1接收机故障，为方便对比分析，同样选用6号卫星的数据进行分析，图7和图8为历元10 000至12 000之间6号卫星的PRSCA和B值及其门限值曲线，图9为移除基准站1后6号卫星对应3个基准站B值变化曲线。

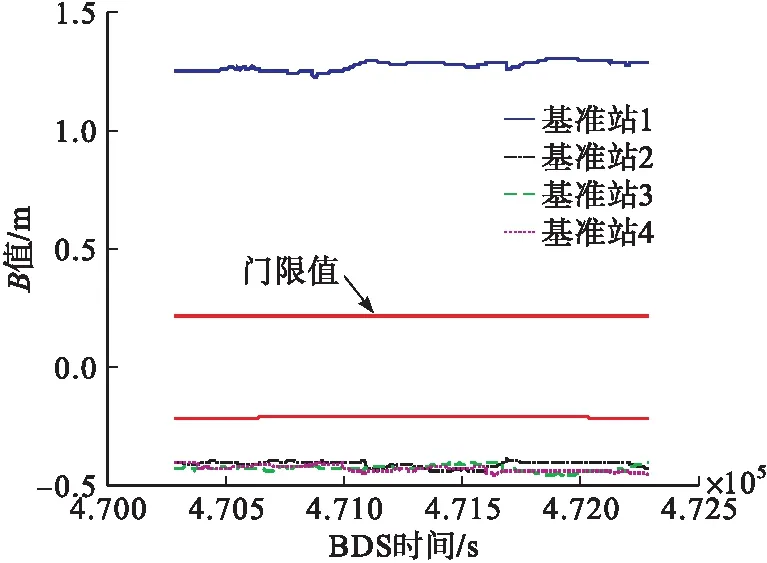
图8 基准站1接收机故障时6号卫星的B值及其门限值

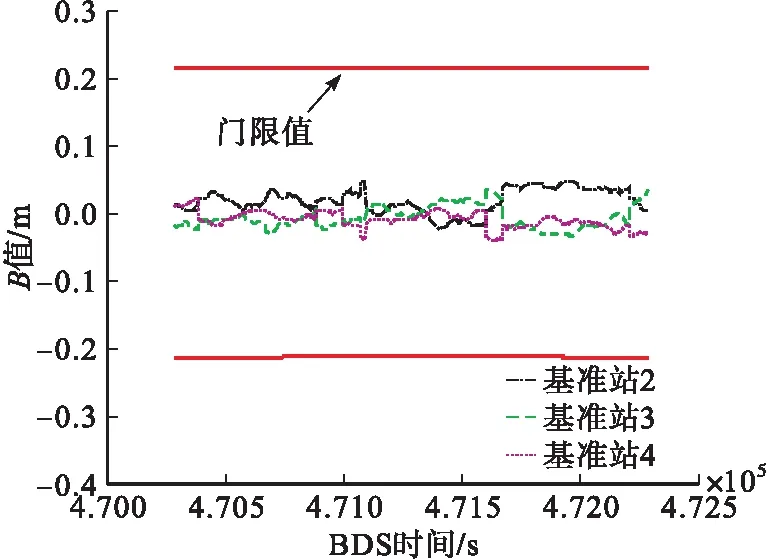
图9 移除基准站1接收机后6号卫星的B值及其门限值

由图7、图8可以看出，在470 288 s至472 288 s之间，当基准站1接收机发生故障时，对应的B值会发生较大幅度的跳变，同时在该时间段内，其他3个基准站对应的B值也出现较为明显的变化，超出了检测门限值范围，因此无法区分故障接收机。进一步根据本文图1给出的MRCC算法流程，通过比较4个基准站B值的大小，可以将基准站1予以移除，然后计算得到剩余3个基准站的B值，由图9可以看出，基准站2～4的B值在门限值范围以内，说明此时有3个基准站接收机可用，从而实现了故障接收机的检测与隔离。

5 结语

GBAS地面系统中MRCC算法主要用于检测地面基准站接收机计算得到的差分校正值是否具有一致性，针对传统基于极大似然估计准则的MRCC算法无法区分GBAS地面系统基准站接收机故障来源问题，本文在对GBASB值计算理论分析的基础上，给出了一种能够有效确定接收机故障的MRCC算法处理流程，并提出了一种基于高斯膨胀法的B值门限值计算方法。通过实验室研制的GBAS原型系统验证了所提出方法的有效性，地面系统接收机无故障时，B值在门限值以内，一旦某个基准站接收机发生故障，则能够有效识别该故障并进行隔离，后续需要进一步对该方法的完好性进行评估。