设计模型 换个角度学科学

陈染

计算机刚刚出现的时候，人们就尝试用计算机解决科学问题。在传统的科学研究中，科学家会对问题提出相应的假设，再通过设计实验验证假设。而计算机更注重于模型的构建，通过模型对科学问题进行预测和假设。计算思维与科学思维并不是非此即彼的，它们互相补充，共同促进科学的进步。

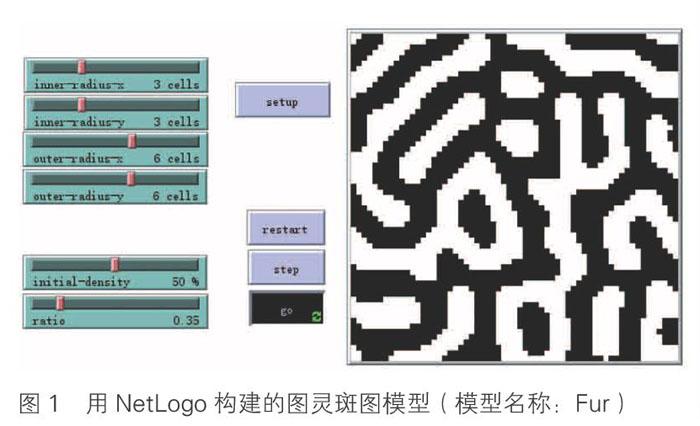
一个著名的例子是阿兰·图灵（AlanTuring）运用计算思维对生物学的研究。众所周知，图灵为计算机的发明提供了理论基础，被称为“计算机之父”。可鲜为人知的是，在图灵晚年，他将研究精力放在生物学上，但他并不是只沉浸在实验室中，作为一名计算机科学家，图灵试图通过构建计算机模型解释生物学现象。1952年，也就是图灵生命的最后一年，他完成了论文《形态发生的化学基础》，这篇论文运用计算机模型的方法探讨了动物身上花纹的形成规律。在模型中，图灵假想了2种作用相反的物质：激活剂和抑制剂，通过这2种物质的互相对抗形成不一样的图案。通过构建这个模型，图灵发现只需要改变激活剂和抑制剂的参数，就能够构建出斑马、豹子、斑点狗等动物的图案。为了纪念图灵的贡献，人们把能够通过图灵提出的模型形成的图案称之为“图灵斑图”（图1）。图灵的这篇文章促成了一个全新的交叉学科领域“计算生物学”的产生。

这篇论文不仅在生物学研究上产生了重大影响，其所运用的新思路在物理、化学乃至社会科学领域也产生了深远的影响。换一种思路，一些以前看上去棘手的问题突然变得简单。作为教师，我们也可以将这种思路运用于科学课程的学习中，通过构建模型，更清楚地解释科学课程中的现象，换一个角度也许学生的困惑便会迎刃而解。

探究物种的演化

自然选择是中学生物课中的一个重要知识点。物竞天择，适者生存，为了生存，有的生物演化出令人惊叹的保护色，保护它们不被天敌发现。生物课本中所讲的桦尺蠖便是一个典型的例子。

桦尺蠖是一种生活在桦树上的蛾子，它有深色和浅色2种色型。19世纪中，科学家在曼彻斯特作了一个调查，发现这里的桦尺蠖大多数是浅色型，只有少数深色型。100年后，曼徹斯特已经成为一座工业城市，工厂的浓烟熏黑了白色的桦树皮。当科学家来到同一个地方再次进行桦尺蠖调查时，发现这里的桦尺蠖大多数是深色型的，浅色型反而成了少数。科学家认为在自然的选择之下，桦尺蠖发生了基因频率的变化，相对于浅色型的SS基因，携带深色型的ss基因的桦尺蠖更容易生存下来。

在这个案例中，我们通过科学家的角度探究自然选择对基因频率变化的影响。我们还可以换一个角度，从捕猎者的角度探究自然选择对基因型的影响。NetLogo的模型Bug HuntCamouflage（捕猎虫子，图2）为我们提供了这样的思路。

与其说这是个模型，不如说这是一个代入式的游戏。点击go运行模型时，我们会看到右侧的花田中会长出一只只颜色各不相同的虫子，你的鼠标也变成了鸟的形状，你所要做的任务就是尽可能多地吃掉虫子。

这个模型模拟的是自然环境下虫子被天敌捕食时产生的自然选择。每隔一段时间，虫子就会繁殖，生下来的大多数后代与前一代的颜色相同，少数情况会发生基因突变变成其他颜色。一开始我们会很容易地找到虫子，过了一段时间后，捕食虫子变得越来越难，我们可以通过模型左侧的捕虫数与时间的关系图直观地看到这种变化（图3）。

当我们觉得已经难以找到虫子的时候，暂停模型的运行，看看在这场捕虫游戏中你收获了什么吧。

点击模型的flash按钮，未被捕捉的虫子会闪烁。我们会发现并不是所有的虫子都被捕捉，有些虫子在我们的捕捉下幸存下来，并演化出保护色，不容易被我们发现。模型左侧下部有6个直方图，上面的3个直方图表示的是当前虫子的色彩、明暗和饱和度分布图，而下面的3个图表示的是游戏开始时的虫子色彩、明暗和对比度的分布情况。通过2组图的比较，我们可以直观地看出虫子颜色是如何变化的（图4）。

那么，自然选择下虫子的基因型如何变化呢？这个模型巧妙地利用计算机颜色数值表示了虫子的基因型。我们知道，在计算机中，1个颜色由红绿蓝（RGB）三原色的不同配比组成，每个颜色的取值范围从0-255，黑色的RGB值是0，0，0，意味着红、绿、蓝的取值都是0;白色的RGB值是255，255，255，通过这样的表示方法，计算机总共可以显示16 777216种颜色。这3种原色的数值组成了一个三维向量，在模型中我们用它代表虫子的基因型。我们通过计算每一个向量的标准差，就可以得知基因型的变化。模型右侧花田图片下方的图便是向量标准差随时间的变化图，标准差越高，意味着虫子的基因型越相似，也意味着虫子的颜色越接近。看看在我们捕猎期间，虫子的基因型发生了怎样的变化（图5）。

我们看到，随着猎食者的捕食，虫子基因型的标准差越来越高，说明虫子的基因型越来越相似。过了一段时间，我们发现标准差变小了，意味着虫子之间的基因型差异变大了，这发生了什么呢？仔细观察生存下来虫子的颜色，我们会发现一个有意思的现象，分布在花上的虫子颜色更接近花的颜色，分布在叶子上的虫子更接近叶子的颜色。这个现象意味着经过自然选择之后，虫子分化为居住在花上的和居住在叶子上的2个生态位。

这个模型还可以帮助我们探究更多的问题，例如，动物的体型会对保护色产生什么影响，动物的基因突变频率是否有利于它的生存，动物的后代迁徙距离对保护色有什么影响等。

我们看到，在捕猎虫子模型中，我们并没有告诉虫子如何生成保护色，而是使虫子根据几个简单的规则活动，或者说这是模型的3个算法。

·鸟（玩家）会捕食虫子，被捕食的虫子从模型中消失;

·每过一段时间，虫子会生出新的虫子，新的虫子离原有虫子有一定距离;

·生出来的虫子大概率会延续上一代的颜色，小概率会突变成随机颜色。

这个模型可以设置不同的环境，我们发现，只需要构建出这几条规则，无论环境如何变化，虫子都可以很好地融入环境中。当然，现实中的自然选择比我们看到的复杂得多，模型是对现实的简化，我们不关注现实中复杂的变量，而是抽丝剥茧，关注最核心的问题，这也就是计算思维研究问题的方法。

探究植物的生长

自然选择不仅发生在动物中，植物同样也发生着自然选择。例如，很多人喜欢养多肉植物，多肉植物吸引我们除了质感厚实可爱之外，我们还发现它的叶片分布非常均匀，排列得很有规律，呈现出某种迷人的秩序之美。不只是多肉植物，很多植物，例如向日葵的花盘，也会呈现出同样的迷人的排列。在课本中我们常常把它们当成自然界的数学之美的案例。

我们可以进一步地探究这些迷人的秩序是如何形成的。科学家发现，图案的形成与叶子的生长角度有关。科学家对很多轮生叶序植物进行研究，发现很多轮生叶序植物长出的第1片叶子和第2片叶子的夹角度数是137.51°。137.51°是一个神奇的角度，如果2片叶子的夹角是137.51°，那么它的补角就是222.49°，这2个角度的比值接近黄金分割比例0.618，因此，137.51°也被称为黄金角。为什么那么多的植物会选择黄金角呢？我们可以通过模型进行探究。

NetLogo模型库中的Sunflower模型（图6）很好地模拟了不同角度下叶子生长的情况。在这个模型中，我们将植物的整体形状的形成分解为每一片叶子的生长模式，并用“海龟”来代表叶子。

在这个模型中，叶子的生长行为遵守以下几个规则。

·叶子从画面原点开始生长，生长方向与上一片长出的叶子保持一定的夹角;

·叶子会逐渐远离原点;

·叶子会逐渐长大。

在模型中，我们可以调整叶片夹角的比例，探究不同比例会形成怎样的图案，将比例设置成0.617、0.618 034和0.619，运行模型，我们看到模型会生成3种不一样的花（图7）。

我们看到，尽管比例上只有0.001的微小差别，转换成角度只有0.36°，但花的形状却非常不一样。比例为0.617和0.619的花都会产生空隙，有些叶子还会互相堆叠，导致空间的利用率不高。而只有遵循黄金角度的花会充分填满花盘的空间，同时又不会发生叶子的堆叠。在现实中，这样的叶子排列能够更充分地利用空间，更具有竞争优势。因此，在自然选择中，很多植物的叶片都采用了黄金角的生长角度。

用模型探究概率问题

概率论是中学数学中非常重要的一部分，也是比较适合用于开发计算机模型的主题。其中， “三门问题”是中学概率论中一个很有趣同时又很令学生困惑的问题，理解三门问题将有助于学生更好地学习条件概率。三门问题的表述如下。

三门问题又叫蒙提霍尔问题。它源自20世纪60年代的美国电视节目“Let's Make ADeal”。参赛者经过重重闯关后，会看见三扇关闭的门。其中一扇的后面藏着1辆汽车，而另外两扇门后面则各藏着1只山羊，参赛者想要获得汽车而不是山羊。此时，参赛者指定了一扇门，但未去开启它的时候，知道门后情形的节目主持人会开启剩下两扇门中背后是山羊的一扇门，并询问参赛者： “是否转换选择指定另一扇门？”

这时候参赛者就产生分歧，有人选择转换指定，有人选择不转换，他们的思维方式是怎样的呢？

選择转换指定的人：无论选择哪一扇门，主持人都会打开另外两扇门中没有汽车的一扇，在剩下两个答案中排除了一个选项，那意味着剩下的一扇门有中奖的概率更高，所以选择转换指定的门。

选择不转换指定的人：无论选择哪一扇门，主持人都会打开一扇有山羊的门。没有打开的两扇门中，其中一扇门是汽车，另一扇门是山羊，所以每扇门的中奖概率是1/2，因此转换与否不影响中奖概率，因此选择不转换。

这两种思维看上去都很有道理，哪一种是正确的呢？试一试就知道了。概率实验需要重复多次才能得出正确的结论，在现实中反复进行这个实验费时费力、效率低下，而运用计算机构建模型，可以在极短的时间内进行成百上千次实验，在现实中可能需要数十个小时完成的实验，在计算机里只需要几秒钟就完成了。NetLogo模型库中的Three Doors便是让“海龟”自动进行重复实验的模型。

这个模型让数百只“海龟”不停地进行三门游戏。实验开始时，每只“海龟”按照以下几条规则活动：

·每只海龟有3个选项，其中1个选项是获奖选项;

·海龟在3个选项中随机选择1个;

·去掉剩余2个选项中不是获奖选项的1个;

·海龟选择是否转换选择（黑色海龟表示永远选择转换，白色海龟表示永远选择不转换）;

·如果海龟选择的是获奖选项，则奖励向前前进一步，如果不是获奖选项，则不进行任何操作。

设计了海龟的行为规则之后，我们就可以将它转换成计算机能够理解的程序，教师可以引导学生设计模型程序的流程图（图9），清晰地顺理模型设计思路，这种方法有助于我们设计自己的模型。

这个模型有2种运行模式，点击gradation即可切换。当gradation开关关闭的时候，点击运行，我们看到黑色的海龟跑得比白色的海龟更快;当gradation开关开启时，点击运行，海龟作出随机选择而不是固定选择，颜色越深的海龟更倾向于选择转换，颜色越浅的海龟更倾向于选择不转换。我们同样发现越深色的海龟跑得越快。通过这个实验，我们看到选择转换的海龟更容易获得奖品，也说明了第1种思维方式的正确性。

通过这个模型，我们在计算机里做了成千上万次实验，并通过“海龟赛跑”的形式直观地展现实验结果。如果有条件，我们可以引导学生自己通过Pwthon或Scratch建立三门问题模拟，相信对学生理解背后的条件概率有更大的帮助。

用蒙特卡洛法计算圆周率

我们看到计算机可以在很短时间内将一个程序重复执行成千上万次。这种优势不仅可以让我们认识概率问题，科学家还通过它解决了许多难以解决的问题，围棋AI程序便是其中的一个例子。围棋有19×19总共361个交叉点，每个交叉点可以有黑棋、白棋、没有棋子3种情况，除去围棋规则不允许和对称的情况外，总共约为2×10170种情况，比整个宇宙的原子还多，复杂度之高计算机显然无法计算所有情况。那么，著名的人工智能围棋程序AlphaGo是如何在如此复杂的选择中简化局面作出最佳选择的呢？

Alpha Go战胜人类的秘密是依靠蒙特卡洛树搜索和深度神经网络。其中，蒙特卡洛法的作用就是简化局面，使计算机无须遍历所有情况，即可在有限的时间内找出最佳一着。

蒙特卡洛法又叫模拟法，它源于20世纪40年代美国开启研制原子弹的“曼哈顿计划”。在研制原子弹的过程中，冯·诺依曼提出了一种新的算法，它最大的特点就是“蒙”。面对一个高度复杂的系统，蒙特卡洛法通过大量随机模拟，估算系统的最优解。蒙特卡洛算法就像盲人摸象，盲人无法看到大象的全貌，只能靠摸猜测大象的样子，有人摸到象鼻子，有人摸到象尾巴，有人摸到象腿，怎样了解大象的全貌呢？我们可以找来尽可能多的盲人，让盲人随机摸大象，然后将所有盲人的答案集合起来，我们就能估计出大象的全貌。

在计算机发明之前，人们已经产生了“布丰投针”实验等用随机现象认识复杂系统的思想，但囿于无法产生大量样本，布丰投针实验更像是数学家闲暇之余的游戏。计算机的发明，使得快速生成大量随机样本成为可能，也让它从数学游戏变成了真正实用的工具。为了更好地了解蒙特卡洛法，我们可以用NetLogo设计一个蒙特卡洛法计算圆周率的程序。

设计蒙特卡洛法计算圆周率的思路核心是我们需要构造一个办法让圆周率丌与某个概率联系起来。计算圆周率，我们首先要联想圆，圆的面积公式是S=丌，，我们可以利用圆面积构造概率，而剩下要做的就是想办法消掉，。

我们可以这样构造模型：作圆及外切正方形。设圆的半径为r，则外接正方形边长为2r。然后我们在正方形内随机投点，设投点总数为a，落入圆内的点数为b，那么，投点落入圆内的概率b：a为S圆：S方，即πr2/4r2=π/4。这样，我们就可以将概率与圆周率丌联系起来。

有了思路，我们就可以通过NetLogo程序设计模型。我们在模型的“瓦片”上作圆，并将“海龟”投点到模型中，通过判断海龟的位置是在圆内还是在圆外，计算出圆周率丌的数值。我们可以设立“初始化”和“运行”2个按钮，分别对它们进行编程，模型的程序流程图分别如图10。

我们用变量total统计总共的海龟数，用变量turtlein_green统计落在绿色圆内的海龟个数。我们通过监视窗估算圆周率丌的值，计算方法为（turtlesin_green/total）*4。在左下方的图表计算的是估算值与真实值的误差率。我们看到，一开始投点比较少的时候，误差率非常高，但经过了10万多次投点采樣后，我们将能够将误差率降低到0. 02%（图11）。

通过这个模型，我们可以归纳出蒙特卡洛法的特点。蒙特卡洛法需要多次重复实验：需要多次随机采样才能了解一个系统，与之相对的，蒙特卡洛法精确度较低，我们需要进行数万次乃至数十万次投点，才能达到比较满意的结果。但蒙特卡洛法的计算较为简便，对于复杂度比较高的计算，蒙特卡洛法可以简化计算量，也是这个特点，蒙特卡洛法的泛用性比较高，对于不规则的图形，普通的数学方法可能难以通过积分等方法计算其面积，而蒙特卡洛法能够快速估计不规则图形的面积。这种利用计算机生成大量随机样本的思维模式，正是计算思维在数学领域的应用。