等效替代思想的应用例析

赵艳光

等效替代法在物理问题的解决过程中具有重要作用．事实上,等效替代的思想几乎渗透于高中物理的各部分,如力(或运动)的合成与分解、等效电源、等效电阻等都是等效替代思想的具体应用．笔者结合两道例题,感受等效替代思想在解决具体问题中所展现的魅力．

1 引入等效电阻,分析远距离输电问题

远距离输电问题涉及的物理量多,且各物理量相互影响,相互制约,其中一个因素的变化,常会引起一系列的动态变化,可谓牵一发而动全身.面对此类问题,学生往往束手无策．等效电阻的引入,可简化该类问题的思维流程,使复杂而冗长的推导过程变得简洁明了．

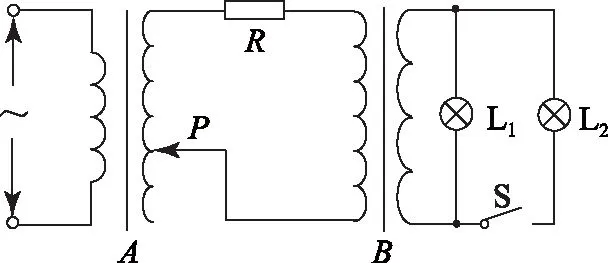
图1

A. 仅闭合S,L1变暗

B. 仅闭合S,输电线路的发热功率变小

C. 仅将滑片P上移,L1变亮

D. 仅将滑片P上移,输电线路的发热功率变小

图2

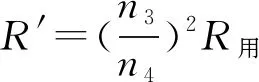
2 构建等效重力场,求解竖直平面内圆周运动的极值

重力场本质上是恒定力场,对于由恒定场叠加后的复合场问题的研究,都可借鉴重力场的研究方法,这种从力的合成的角度而引入的等效替代,使多力问题变为单力问题,将陌生的场景转化为熟悉的场景,从而使复杂的问题在构建等效场的过程中得以顺利解决．

(1)小球做圆周运动过程中的最小速度．

(2)施加的最小冲量.

图3 图4

总之,等效替代思想作为研究物理问题的一种重要方法,在高中物理中有着非常广泛的应用,其实质是效果相同,其特征是等效变换,体现的是对问题深层次的理解,是综合素质与能力的集中反映,也是该类问题在高考中频繁出现的原因所在．