多层氧化石墨烯单轴拉伸行为的分子动力学模拟

杨 志，陈玉双，彭洛凡

（西华大学材料科学与工程学院，四川 成都 610039）

多层氧化石墨烯由单层氧化石墨烯堆垛而成，其表面及层间是随机分布的羟基、环氧基等化学活性官能团[1-2]，赋予其优异的物理化学性能。由于表面官能团具有良好的可修饰性，其层间距易调、可控，多层氧化石墨烯在离子或气体分离、水处理及净化等领域具有广泛应用前景[3-6]。应变是调控多层氧化石墨烯的层间距的重要手段[7-8]，材料自身的力学性能及变形行为决定了应变调控的可行性；因此，研究多层氧化石墨烯力学性能及变形行为是揭示层间距应变调控规律的基础。

围绕单层氧化石墨烯力学性能的研究已被广泛报道[9-12]。不同氧化石墨烯材料的力学性能存在显著差异，并受到氧化官能度(R)、取向及温度等因素影响。作者最近研究[12]发现，氧化石墨烯的断裂行为表现出R 依赖性，当R＜30%，裂纹从环氧基中扭曲的碳碳键萌生，并沿Z 轴方向扩展；当R＞30%，主要依靠点缺陷的合并萌生裂纹。而在此前，Suk 等[13]结合原子力显微镜和有限元方法，测得单层氧化石墨烯的弹性模量可达(207.6±23.4)GPa。Cao 等[14]利用计算机模拟方法研究氧化石墨烯的断裂机制，发现裂纹沿着与含氧官能团相连或相邻的面内碳碳键扩展。在单轴载荷下，氧化石墨烯薄膜的拉伸强度高达(12±4 )GPa，接近单层氧化石墨烯的本征强度，比氧化石墨烯块体本征强度高出一个数量级[15]。在机械破坏过程中，局部区域的脆性断裂，即从氧化石墨本体常见的层间断裂到主导单层氧化石墨烯失效的面内断裂机制转变，是导致氧化石墨烯薄膜强度增高的原因。目前针对多层氧化石墨烯的力学性能的理论研究仍然非常有限。基于分子动力学模拟方法在揭示纳米材料力学性能及其变形机制方面的显著优势[9-12]，本文拟采用该方法模拟多层氧化石墨烯单轴拉伸过程，揭示多层氧化石墨烯的氧化官能度、堆叠层数及温度对材料体系弹性模量、极限强度及极限应变的影响规律，以期为该介观尺度材料的应用提供理论指导。

1 模拟方法

利用分子动力学软件(large-scale atomic/molecular massively parallel simulator, LAMMPS)[16]进行拉伸模拟。选择Reaxff 势函数来描述碳、氢、氧3 种原子之间的相互作用：

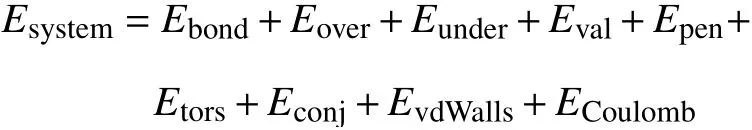
其中：Ebond是键能；Eover是原子过配位补偿能；Eunder是原子欠配位补偿能；Eval是价角能；Epen是中心原子过/欠配位的补偿能；Etors是扭转角能量；Econj是共轭效应对分子能量的贡献部分；EvdWalls是非键范德华尔相互作用；ECoulomb是非键库仑能。与传统反应力场相比，Reaxff 势包括健级/键能关系，允许在模拟过程中成键或断键，因此能有效量化氧化石墨烯系统中的不同原子之间的成键和非键相互作用[17-18]。

多层氧化石墨烯一般是由单层氧化石墨烯堆垛而成。计算模型通过Matlab 软件编程实现，在石墨烯六边形架构和基本物性参数约束下，随机选择环氧化位点和羟基化位点，并通过位点数量及其比例控制氧化官能度。创建模型的尺寸为100 Å×100 Å，厚度依赖于样品体系。在进行单轴拉伸模拟之前，采用共轭梯度算法使初始氧化石墨烯模型局域能量最小化：用Nose-Hoover 恒温器恒温，将模型在温度为300 K 的NVT 系综下弛豫200 ps，如图1 所示。加载过程在等仿射变换下将氧化石墨烯的原子膨胀到目标位置，并沿加载方向(x 轴方向)扩展模拟单元，实现了单轴拉伸。面内各方向为周期性边界条件，面外为自由边界条件。拉伸速率为0.000 1 ps-1。

图1 多层氧化石墨烯模型：（a）正视图；（b）透视图

2 结果与讨论

2.1 双层氧化石墨烯的结构优化

双层氧化石墨烯(BGO)模型序列的初始层间距 以0.5 Å为 步 长，从3.0 Å逐 渐 增 加 到7.0 Å。BGO 模型序列中，氧化石墨烯的R 一层设定为10%，另一层分别设定为10%、20%、30%、40%和50%，并依次标记为样品10%～10% (Ⅰ)、10%～20% (Ⅱ)、10%～30% (Ⅲ)、10%～40% (Ⅴ)、10%～50% (Ⅳ)。R 可定义为“与氧原子成键的碳原子占总碳原子数的百分比”，其值可由公式(1)计算：其中， NO、 NH、 NC分别为模型中氧原子、氢原子和碳原子的数目。以氧化程度较小的石墨烯为例，假设O/C 为1/5，则20%＜R＜40%。

图2(a)为不同层间距BGO 弛豫过程的能量曲线。据此判断，4.5 Å为双层氧化石墨烯的最优层间距。石墨烯表面随机分布羟基、环氧基等官能团，局部分布差异诱导不同程度的晶格畸变，进而使氧化石墨烯表面呈现不均匀起伏(如图1 所示)。图2(b)为弛豫前后原子沿着z 轴方向的分布，D 和d 分别表示弛豫前后的平均层间距。D 和d 的差异表明，弛豫前后，平均层间距发生显著变化。

图2 （a）不同层间距的双层氧化石墨烯弛豫过程能量曲线；（b）弛豫前后，原子沿Z 坐标轴的分布图

2.2 氧化官能度(R)对双层氧化石墨烯力学性能的影响

石墨烯的六边形基本结构具有各向异性特征，氧化后平面六边形结构被破坏，具有了三维空间构象[19-20]。为验证氧化石墨烯的变形行为及力学特性是否也具备各向异性特征，分别沿着氧化石墨扶手椅(armchair)方向和锯齿型(zigzag)方向施加单轴拉伸载荷，应力-应变曲线如图3 所示。比较zigzag 方向和armchair 方向可知，R 相同时，应力-应变曲线走势基本一致，极限强度随着R 的升高而降低，极限应变几乎不受影响。可以预测，与单层石墨烯、单层氧化石墨烯不同，双层氧化石墨烯受到堆垛层数及R 的影响，其变形行为趋于各向同性。

为了定量验证，提取E、σ 和ε 等力学参量，并对R 作图(如图4 所示)。随着R 增大，E 从250 GPa (Ⅰ)减小至100 GPa (Ⅴ)，σ 从24 GPa (Ⅰ)减小到13 GPa (Ⅴ)，ε 基本维持在12%。由于含氧官能团的加入使较强的sp2杂化碳转化为弱的sp3杂化碳，从而降低了氧化石墨烯的能量稳定性，使得E 变小。此外，含氧官能团在氧化石墨烯表面的随机排列导致沿锯齿型方向的弹性模量略小于沿扶手椅方向弹性模量。例如，如果附着在平行于锯齿型方向的C—C 键上的环氧官能团的比例大于附着在其他C—C 键上的官能团，这种排列将导致沿扶手椅方向断裂应变的增加。

图3 不同R 值的氧化石墨烯构成的双层氧化石墨烯沿着扶手椅方向（armchair）和锯齿型（zigzag）方向拉伸时的应力-应变曲线

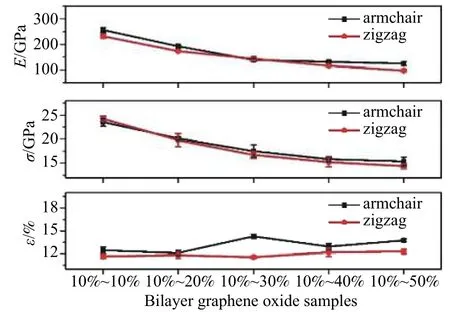
图4 弹性模量（E）、极限应力（σ）及极限应变（ε）随R 的变化关系

图5 为5 组模型拉伸断裂前后的原子结构演化图。对模型Ⅰ而言，两层石墨烯的氧化官能度相同，裂纹萌生及扩展位置相同。随着层间氧化官能度差异的扩大，裂纹的萌生位置及扩展程度逐渐分化。特别强调，R 为10%的BGO 层更易发生破坏。因为R 越大，沿着拉伸方向的晶格参数畸变越大，具有容纳更大变形的能力。

图6 为40%的BGO 层断裂过程中局部构型/象的演化。羟基诱导的结构演变如图6(a1)至图6(d1)所示，与羟基相邻的碳碳键依次首先发生断裂、闭环重构、再次断裂及形成碳链等过程。环氧基诱导的结构演变如图6(a2)至图6(d2)所示，环氧基上的碳碳键优先断裂，碳六环扩展为含氧七环结构，最后发生开环开裂。分析表明，羟基和环氧基诱导裂纹的机制各不相同，环氧基的引入虽然产生了较大的晶格畸变，断开的环氧碳碳键却能够容纳更大的拉伸应变。

图5 双层氧化石墨烯断裂过程中微观结构的演化

图6 断裂前后原子结构的演化：（a1）和（a2）：ε=11.2%；（b1）和（b2）：ε=13%；（c1）和（c2）：ε=15.2%；（d1）和（d2）：ε=17.8%

2.3 温度及堆垛层数对氧化石墨烯力学性能的影响

图7 (a)表示双层氧化石墨烯的E、σ 及ε 随温度的变化规律。E 随温度升高变化不大，在200 GPa 到225 GPa 之间。σ 对温度敏感，随温度升高从22 GPa 减小到16 GPa，降幅高达27%。ε 随温度的变化更加复杂，在100 K 时，极限应变约为16.5%，升温至200 K 时，极限应变快速降低到12%左右；继续升温，极限应变反向增大。这是由于温度对C—C 及C—O 键有活化作用，双层氧化石墨烯和单层氧化石墨烯的变形过程具有相似的温度依赖特征[21]。

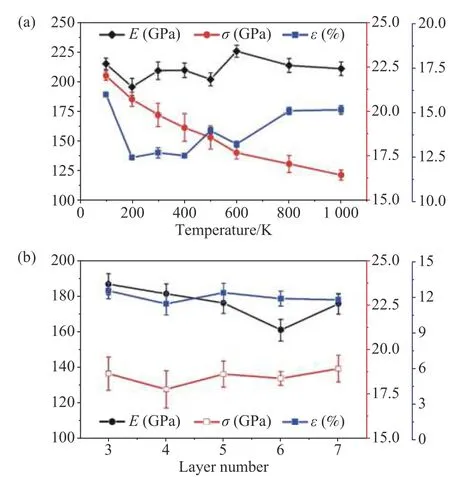
图7 温度（a）和堆垛层数（b）对E、σ 及ε 的影响

图7 (b)是E、σ 及ε 随堆垛层数的变化规律。以R=10%的氧化石墨烯为例，模拟3～7 个堆垛层的氧化石墨烯的单轴拉伸过程。结果显示，氧化石墨烯的E 随层数的增加略微降低，三层氧化石墨烯的E 约为188 GPa，而七层氧化石墨烯的E 约为175 GPa。模量的微小变化可能源于层与层之间的润滑作用[22]。此外，σ 及ε 分别为18.4 GPa 和12%，随厚度变化波动幅度不大。

3 结论

本文通过分子动力学方法模拟了多层氧化石墨烯的单轴拉伸过程，探讨了氧化官能度、堆叠层数和温度对弹性模量、极限强度与极限应变的影响规律。结果表明：1)多层氧化石墨烯最佳层厚约4.5 Å；2)受到堆垛效应及氧化官能度的影响，双层氧化石墨烯趋于各向同性，屈服强度随着氧化官能度的升高而逐渐降低，屈服应变变化较小；3)弹性模量随温度起伏变化不大，极限应力随温度的升高而降低；4)极限应变随温度的变化较为复杂，呈现先减小后增大的变化趋势；5)氧化石墨烯的弹性模量、极限应力和极限应变受厚度变化影响较小。