Design and experimental testing of a control system for a morphing wing model actuated with miniature BLDC motors
2020-06-11TeodorLuinGRIGORIEShehryrKHANRuxndrMihelBOTEZMhmoudMAMOUYoussefMEBARKI
Teodor Luin GRIGORIE, Shehryr KHAN, Ruxndr Mihel BOTEZ,*,Mhmoud MAMOU, Youssef ME´ BARKI
a ETS, Laboratory of Active Controls, Avionics and AeroServoElasticity LARCASE, Montreal H3C-1K3, Quebec, Canada
b Military Technical Academy ‘‘Ferdinand I”, Bucharest 040531, Romania
c Aerodynamics Laboratory, NRC Aerospace, National Research Council Canada, Ottawa K1A0R6, Ontario, Canada
KEYWORDS BLDC motor;Control tuning;Morphing wing;Simulation and experimental testing;Wind tunnel
Abstract The paper deals with the design and experimental validation of the actuation mechanism control system for a morphing wing model.The experimental morphable wing model manufactured in this project is a full-size scale wing tip for a real aircraft equipped with an aileron.The morphing actuation of the model is based on a mechanism with four similar in house designed and manufactured actuators, positioned inside the wing on two parallel lines. Each of the four actuators used a BrushLess Direct Current(BLDC)electric motor integrated with a mechanical part performing the conversion of the angular displacements into linear displacements.The following have been chosen as successive steps in the design of the actuator control system: (A) Mathematical and software modelling of the actuator; (B) Design of the control system architecture and tuning using Internal Model Control (IMC) methodology; (C) Numerical simulation of the controlled actuator and its testing on bench and wind tunnel.The morphing wing experimental model is tested both at the laboratory level, with no airflow, to evaluate the components integration and the whole system functioning, but also in the wind tunnel, in the presence of airflow, to evaluate its behavior and the aerodynamic gain.
1. Introduction
One of the main priorities of each scientific field is the optimization, as long as it generates costs savings. From the aerospace industry perspective, efforts are focused on optimizing the various flight-related procedures, which deliver immediate positive effects on allocated financial resources and on the development of green technologies.This aerospace engineering trend has been sustained over time by governments and industry, by initiating and sustaining research programs and projects carried out in collaboration with research centers and universities.
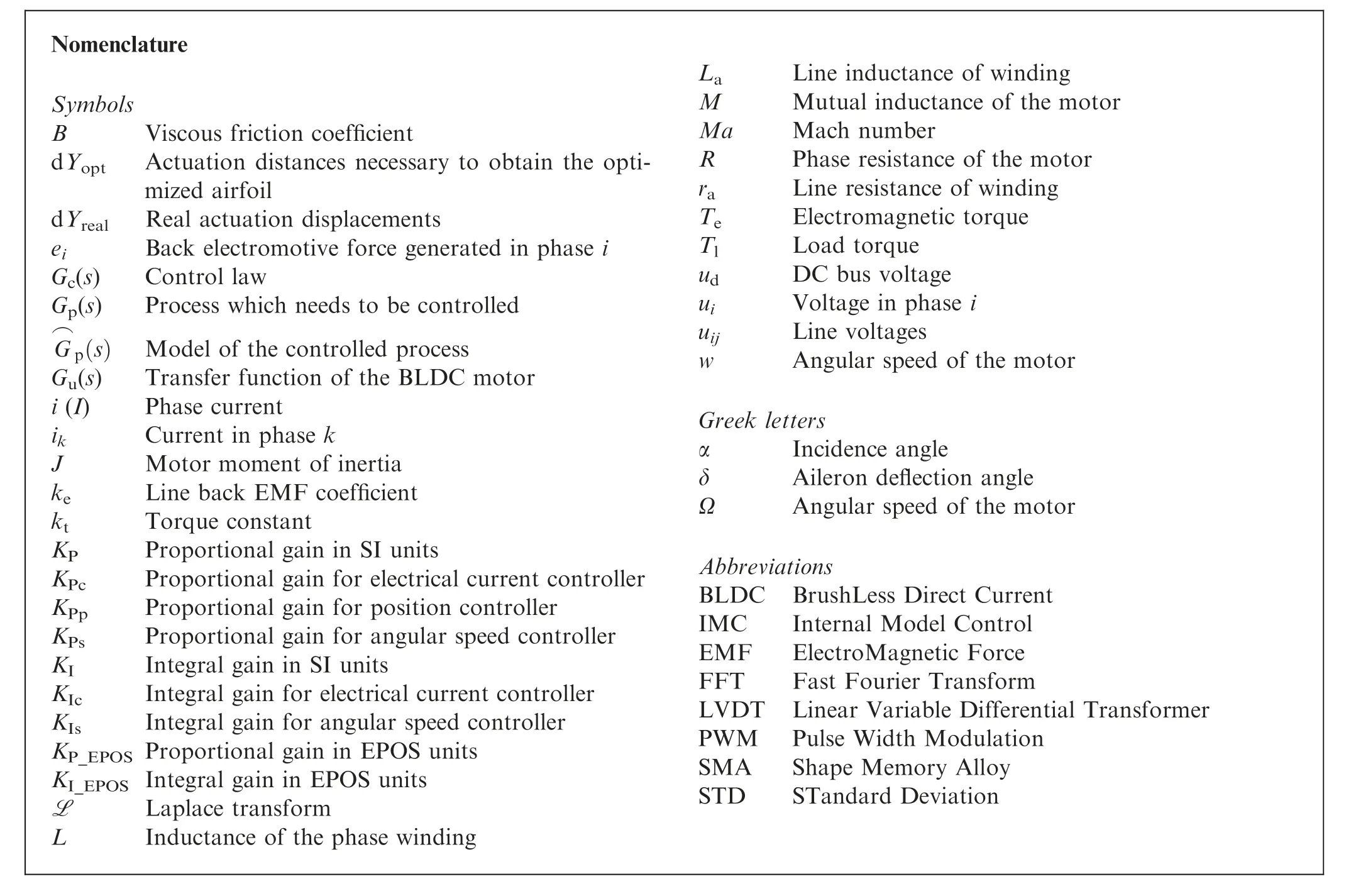
Nomenclature Symbols B Viscous friction coefficient dYopt Actuation distances necessary to obtain the optimized airfoil dYreal Real actuation displacements ei Back electromotive force generated in phase i Gc(s) Control law Gp(s) Process which needs to be controlled G⌒p(s) Model of the controlled process Gu(s) Transfer function of the BLDC motor i (I) Phase current ik Current in phase k J Motor moment of inertia ke Line back EMF coefficient kt Torque constant KP Proportional gain in SI units KPc Proportional gain for electrical current controller KPp Proportional gain for position controller KPs Proportional gain for angular speed controller KI Integral gain in SI units KIc Integral gain for electrical current controller KIs Integral gain for angular speed controller KP_EPOS Proportional gain in EPOS units KI_EPOS Integral gain in EPOS units L Laplace transform L Inductance of the phase winding La Line inductance of winding M Mutual inductance of the motor Ma Mach number R Phase resistance of the motor ra Line resistance of winding Te Electromagnetic torque Tl Load torque ud DC bus voltage ui Voltage in phase i uij Line voltages w Angular speed of the motor Greek letters α Incidence angle δ Aileron deflection angle Ω Angular speed of the motor Abbreviations BLDC BrushLess Direct Current IMC Internal Model Control EMF ElectroMagnetic Force FFT Fast Fourier Transform LVDT Linear Variable Differential Transformer PWM Pulse Width Modulation SMA Shape Memory Alloy STD STandard Deviation
From the point of view of green aircraft technologies development, our research team from E´ cole de Technologie Supe´rieure(E´ TS)in Montre´al,Canada,our Research Laboratory in Active Controls, Avionics and AeroServoElasticity (LARCASE)acted in the next main research directions:(A)development and numerical testing of various algorithms for flying vehicles trajectory optimization;1-9(B) design and validation of different optimal methods for flying vehicles high robustness model identification with the aim to reduce the flight tests number;10(C) design, numerical simulation and experimental testing, including wind tunnel testing, of various experimental models based morphing wing technologies.11-24
Based on the multitude of research studies, projects and programs developed in the last two decades, it seems that for the next generations of aircrafts the morphing wing technology will be a serious alternative to the rigid control surface used currently. Actually, this technology added value on the aerospace field is given by the possibility to improve the aircraft performance by changing various characteristics and match the aircraft state with the requirements of the developed mission. The benefits are related to the flutter and vibration mitigation, drag reduction, fuel costs saving, emissions reduction,flight envelope expansion and improvements in aircraft range.
On the other way,the disseminated results from the worldwide research activities related to this technology proven its huge potential and feasibility. For example, the researchers from the Kentucky University in USA investigated the flow control using shape adaptive surfaces.A piezoceramic actuator bonded with a metallic substrate under the form of a circular arc has been used as adaptive airfoil. The actuator was powered by a bi-polar operational power supply, and tested in a subsonic wind tunnel.The designed architecture proved a good balance between the developed force and the obtained deflection.25Few years later, at the same university a morphing study has been conducted to control the airflow in a mechanism based on the use of some oscillating adaptive surfaces.The study has been realized both by using the numerical simulation, but also by using a modular experimental adaptive wing model, equipped with piezoelectric actuators. The actuation system architecture has been chosen in order to realize a fast actuation and to limit in this way the generation of laminar separation bubbles.26
Another morphing wing experimental model was also developed at University of Bristol, UK, in collaboration with specialists from the University of Limerick, Ireland. The change the wing camber the team used a composite Fish Bone Active Camber (FishBAC) device, equipped with an elastomeric skin and actuated through an antagonistic tendon mechanism. The wind tunnel experimental tests shown an important improvement of the lift coefficient by using this architecture.27
In Japan, in a collaborative research project between the University of Tokyo and Japan Aerospace Exploration Agency was manufactured and wind tunnel tested a morphing wing model based on the use of corrugated structures. The experimental tests suggested that the developed morphable structure exhibited superior properties in lift coefficients.28Over the last fifteen years the German Aerospace Center(DLR)developed a lot of research projects related to the morphing aircraft technologies, financed both from the national resources, but also by using the European Union research founds. In a recent project, the researchers performed the 3D structural design of a large-displacement flexible leading edge(droop nose) equipping a morphable wing for a transport aircraft.29
The research activity in the morphing aircraft domain is intense at this moment, having in mind that here are still a lot of challenges because of the necessary high power required by the implied actuation systems, because of the solutions for the dissipation of the heat generated by the actuators,but also due to their weights and large response times.As a direct consequence of this idea,but also correlated with the actual trend related to the ‘‘all-electric aircraft” concept associated to the green aviation, the ‘‘mechatronics” started to be more and more implied in the aerospace engineering field.
A special place has been reserved by the specialists to the development of electric actuation systems for aircraft, technological direction sustained also through various research projects. As an example, the More Open Electrical Technologies(MOET) can be mentioned.30MOET has been financed in the 6th European Research and Technological Development(RTD) Framework Programme with the main aim to produce a new standard to be used by industry in the design of the electrical systems for the commercial aircraft. As main actuation solutions for aircraft during a lot of time, the actuators based on hydraulic and pneumatic forces started to be replaced with electrical actuators, lightweight and more efficient, especially when they are used to actuate the landing gear or the flight control surfaces.31
2. Research project background
In this context,new researches on morphing wing technologies were carried out by our team in a major research project(‘‘Multi-Disciplinary Optimization 505” (MDO 505)), which targeted to obtain a fuel consumption economy by using these technologies on a real aircraft wing equipped with an aileron,and morphed by using an actuation mechanism with Brush-Less Direct Current(BLDC)electric motors.This project,conducted at E´ TS in Montre´al, was developed in an international research consortium, involving industrial partners as Bombardier Aerospace and Thales from Canada, and Alenia from Italy, and universities and research institutes as E´ TS, E´ cole Polytechnique de Montre´al and the National Research Council of Canada (IAR-NRC) from Canada, and Frederico II Naples University and Italian Aerospace Research Centre(CIRA) from Italy. Within the context of this project, some new numerical studies related to the behavior of the airflow over the morphable wing and aileron were conducted.32-37In addition,a design approach for the aileron position controller was proposed and tested,38followed by the design, numerical simulation and evaluation of various position controllers for the actuators equipping the morphable wing.39-42
The experimental model manufactured in this project is a full-size scale wing tip for a real aircraft, which includes an aileron, as is presented in Fig. 1(a). The obtained model conserved the structure and the stiffness as on the wing of the real aircraft. To morph the model, its upper surface was chosen to a flexible one, manufactured by using some composite materials(see Fig.1(b)).Its actuation is performed by using a system integrating four similar electric actuators, disposed on two lines, which were placed at 32% (Act. #1 and Act. #3) and 48% (Act. #2 and Act. #4) from chord, respectively (see Fig.2).The structure of each actuator includes a BLDC motor and a mechanism which converts rotation movement into linear movement. Due to limited space and the high actuation force requirements imposed by our application, the actuators were manufactured in house using miniature BLDC motors acquired from the Maxon Motor Company.
To monitor the airflow over the wing upper surface,32 high precision Kulite pressure sensors were installed on the flexible skin. They were disposed in equal number on two staggered lines positioned at 0.600 m and at 0.625 m from the wing root section.
The obtained pressure data were real time processed in order to provide information related to the laminar-toturbulent transition location; the Fast Fourier Transforms(FFT)for the acquired pressure data have been real time visualized. As an additional method to evaluate the laminar-toturbulent transition location,but this time over the entire wing upper surface, not only in the pressure sensors sections, the Infra-Red (IR) thermography was used.
In the first phase of the project,a preliminary aerodynamic study was conducted by modifying the original(reference)airfoil for various flight conditions. This allowed for calculation of certain optimized airfoils corresponding to various airflow conditions considered as combinations of incidence angles(α), Mach numbers and aileron deflection angles (δ). This resulted in four displacements (dY1opt, dY2opt, dY3opt, dY4opt)for each optimized airfoil, characterizing the changes from the original (reference) airfoil and corresponding to the positions of the four actuators. All of these displacements were stored in a database to be used for the control system as reference actuation distances necessary to obtain the optimized airfoils. Therefore, the morphing shape control is realized by controlling the positions of the actuators until the real displacements (dY1real, dY2real, dY3real, dY4real) of the morphing skin in the four actuation points equal the desired actuation distances necessary to obtain the optimized airfoil (dY1opt,dY2opt, dY3opt, dY4opt) associated with a flight condition. All of the actuators used the same type of BLDC motor, and therefore,the designed controller is used for all four actuators included in the actuation mechanism.
The results shown in the present paper characterize a part of this second major morphing wing research project (MDO 505) developed by our team, exposing the design and the validation of one of the developed variants for the control system of the morphing actuators integrated in the wing; as design methodology for the control system the Internal Model Control (IMC) procedure has been adopted.42The rest of the paper is organized as follows: Section 2 presents the mathematical and software modelling of the used actuators;Section 3 exposes the tuning of the control loops by using the IMC technique,while Sections 4 and 5 are reserved to the bench testing of the morphing wing control system, respectively to the evaluation of the morphing wing experimental model through wind tunnel testing.
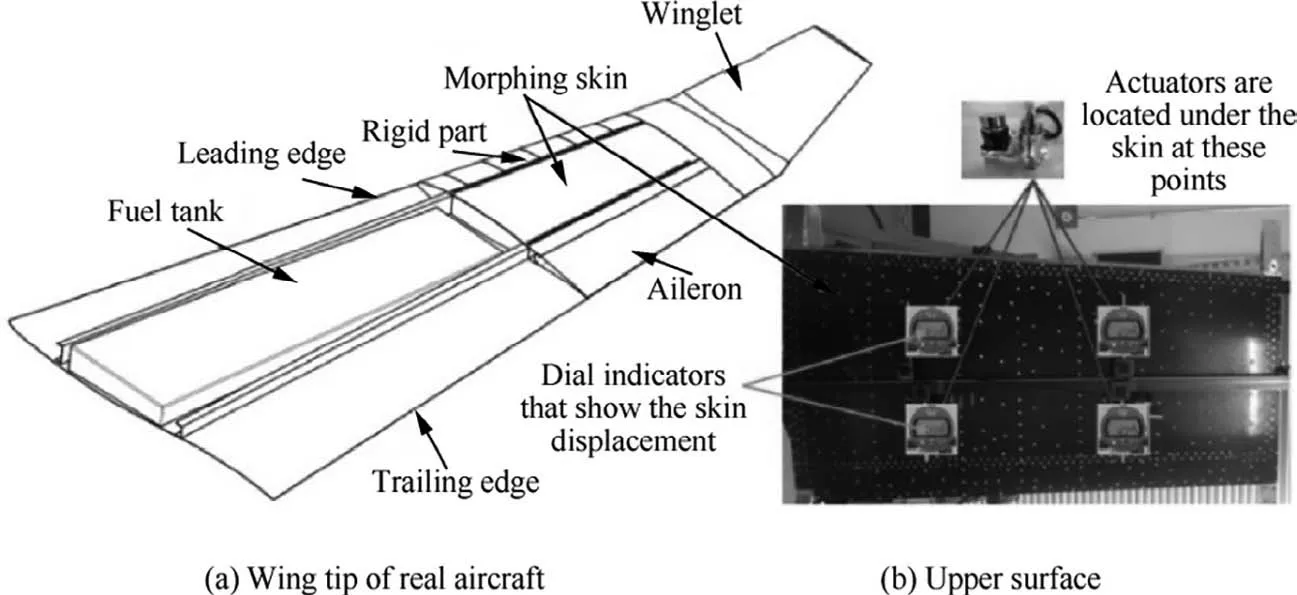
Fig. 1 General architecture of MDO 505 experimental model.

Fig. 2 Actuation system of morphing wing.
Parts from the mathematical model, which are also shown in this paper, describing the first steps in the development of our morphing wing project, have already been presented in few conference papers.39,42The here exposed results reflect the behavior of the experimental morphing wing system as a whole, with numerical simulations, bench testing and wind tunnel testing.
3. Mathematical and software modelling of actuator
Fig. 3 exposes the actuator physical model, which includes a BLDC motor anda mechanism which convertsthe angular movement into linear movement.This mechanism allows the four morphing actuators used in our application to deform,through direct actuation,the flexible skin on the wing upper surface.
In order to design a control system for the actuators which morph the wing, their preliminary mathematical and software modelling is required. The model includes two different parts:(A) the BLDC motor model and (B) the model of the conversion mechanism from angular actuation to linear actuation,linked to the BLDC motor output.
The general objective in the mathematical modelling is to identify a linear model for the actuator under the form of a transfer function (plant model), which can be used in the design phase of the actuator control system. On the other way,the model is further used in a software subroutine to analyze the controlled actuator performance. Having in mind the multitude of the possibilities to drive the actuator included motor, to derive this linear model and its associated transfer function a full bridge drive was considered for the BLDC motor, which operates in the two-phase conduction mode.
From Fig.4(a),39,42,43for the equivalent electrical circuit of a BLDC motor, it results:

where L is phase winding inductance; R is resistance of the phase;M is mutual inductance;iA,iB,iCare electrical currents in the motor phases; uA, uB, uCare voltages in the motor phases; eA, eB, eCare back ElectroMagnetic Forces (EMF)generated in the motor phases.42,43
Because in the most situations the windings of the stator are star-connected, and the neutral point is not brought out to an external physical connection, it is hard to measure the phase voltages. As a consequence, it is recommended to be used a model based on line voltages, having in mind that their measurement is easiest to be done in this configuration.42,43In this situation, the line voltages resulting from Eq. (2) are as follows:

Fig. 3 Actuator physical model.

Fig. 4 Equivalent electrical circuit of BLDC motor and two-phase conduction mode.
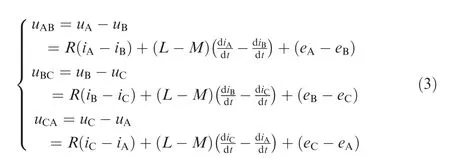
If the phases A and B are conducted and phase C is suspended (two-phase conduction mode), the simplified model in Fig. 4(b)42,43is obtained. Therefore, the relationships between the phase currents iAand iBis:

which also means that:

The line voltage uABfrom Eq. (3) becomes:

Because the eAand eBamplitudes are the same and the signs are opposite, Eq. (6) becomes:

Therefore,

uABis the line voltage; udis DC bus voltage; rais winding line resistance (ra=2R); Lais winding inductance (La=2(L-M)); keis line back EMF coefficient (2eA=kew); w is motor speed of rotation.
The equation characterizing the dynamics of the motor is given by the next expression:42,43

where J characterizes the rotor inertia, B is viscous friction coefficient, Teis electromagnetic torque and Tlis load torque.Denoting the torque constant of the motor as ktresults in a simplified formula for the electromagnetic torque as a function of phase current i,for the two-phase conduction mode,as follows:

From Eqs. (9)-(10) we get:

which, substituted in Eq. (8), leads to:

As a consequence,
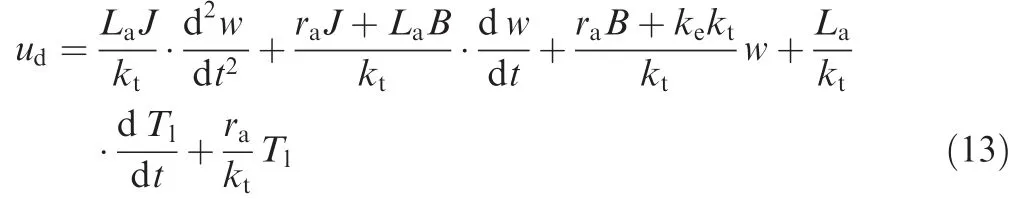
With the Laplace transform, Eq. (13) implies:

where Ω(s)=L{w(t)}, Ud(s)=L{ud(t)}, and Tl(s)=L{Tl(t)}.In another form, Eq. (14) is:

which highlights the dependence between the motor speed and the two main variables which influence it: the DC voltage udand the load torque Tl. It can be easily observed that, for a fixed load,the increase of the udvoltage produces the increase of the motor speed, while, for a fixed input voltage, the increase of the Tlload torque produces the decrease of the speed.
On the other way, Eqs. (8)-(11) lead to:

and

conducting to the following block scheme with transfer functions of the modeled motor (see Fig. 542), which considers the motor loaded with Tl.
To analyze the behavior of the motor integrated in the morphing actuator, a MATLAB/Simulink software model was developed as in Fig. 642(‘‘BLDC model”); it implements both mechanical and electrical mathematical models of the BLDC motor, but also the model of the conversion mechanism from angular actuation to linear actuation. It has as inputs the DC bus voltage Udand the load torque ‘‘T load”, and as outputs the electrical current I, the actuation speed v, expressed in mm/s, and the actuation linear position ‘‘pos”, expressed in mm. In order to conduct numerical simulations, the ‘‘BLDC model” was integrated into the model in Fig. 7,42which contains three control loops acting at the level of the electrical current, actuation speed and actuation position.
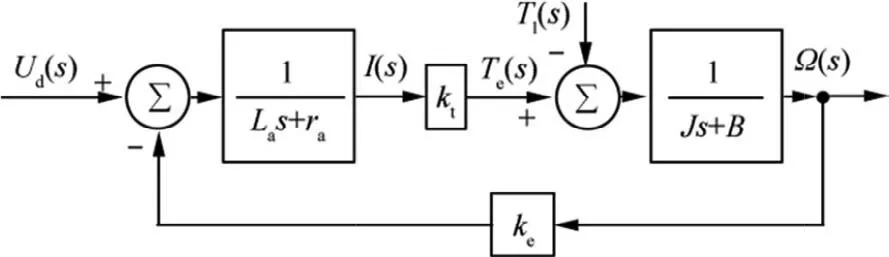
Fig. 5 Motor block scheme with transfer functions.42
The electrical current is measured at the output of the‘‘Electrical TF” block shown in Fig. 6, and is further used to provide feedback in the current control loop as it is shown in the control model presented in Fig.7.According to the control system model in Fig. 7, the ‘‘BLDC model” provides also feedback signals for the speed and position control loops.
4. Tuning control loops using IMC technique
The literature reveals that there have been many control strategies for position control of BLDC motors over the years.PID controllers feature a number of advantages over other controllers, including simplicity of design and implementation,being widely used in many industrial applications. On the other way, the literature shows that there have been many methods for tuning the related coefficients. The best known method was proposed by Ziegler and Nichols, but as a function of the complexity of the controlled systems,various mechanisms were developed over time for tuning the PID and implementing it together with artificial intelligence methodologies. For example, researchers from Xi’an University of Technology designed and developed a new BLDC position servo system using a digital signal processor and fuzzy PID controller. The role of the fuzzy controller was to improve the robustness of the designed system.44
At Howard University in Washington, a smart position control system for brushless motor drives was developed, by combining the fuzzy logic techniques with the neural networks learning abilities.45From another point of view, to obtain a controller with higher robustness, researchers from the National University of Singapore used the sliding-mode control method for a BLDC motor position controller.46In other application, developed at MSL R&D Center in Korea, a control system was designed for a missile actuator based on a BLDC motor and a DSP.The position controller was a classical PID one, while other two loops where used to control the electrical current,with PWM technique,and the speed,with an estimation algorithm with hall sensors, respectively.47At the Institute of Space Technology in Pakistan, a three-phase BLDC motor was modelled and controlled using a PID controller optimized through a genetic algorithm.48The results highlighted more efficient position control for the motor using the proposed methodology instead of the traditional PID tuning method, which used the Ziegler-Nichols algorithm.
Starting from a previous study49communicated in 1986,related to the tuning of PID controllers by using the Internal Model Control (IMC) method, Skogestad proposed in 2001 a new IMC tuning procedure.50It provides poor disturbance response for integrating processes,but generally produces very good responses for set point changes.50-53
The IMC methodology uses the philosophy according to that the control can be realized just if the designed controller includes a representation of the process which should be controlled.More specifically,if in the design process of the control system is taken into account the plant model, then a perfect control system may be obtained.51As an example in the previous idea, it is considered that the process which needs to be controlled is Gp(s), and one model for it has the form G⌒p(s).If the control law Gc(s) is set to be equal with the inverse of the model,

Fig. 6 MATLAB/Simulink model of actuator.42

Fig. 7 Three-loop control system for morphing actuator.42

and the model equals the controlled process,

then the output will track perfectly the reference value set at input. If the plant associated transfer function Gp(s) is minimum phase and invertible, meaning that it has no zeros in the right half-plane, then the controller can be written under the form k(s)=and the open loop transfer function is k(s)Gp(s)=wc/s.42,51Therefore,the closed loop transfer function of the system has the expression T(s)=k(s)Gp(s)/[1+k(s)Gp(s)]=wc/(wc+s), equating with an ideal first-order low-pass filter.42,51
Using the previous methodology,the following results were obtained successively for our BLDC motor control loops.42At the first step,starting from the transfer function characterizing the electrical part of the actuator:
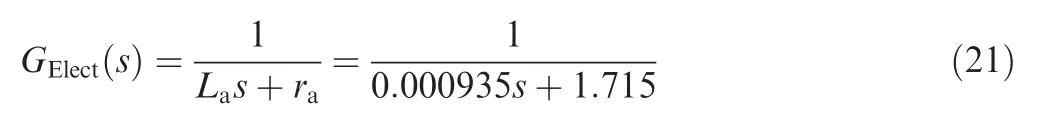
the expression of the control law resulted as:42

The documentation associated to the controlled motor provided the next values for the parameters characterizing the motor phases: ra=1.715 Ω for the resistance, and La=0.935 mH for the inductance.To obtain a suitable value for the coefficient wcthe trial and error method was applied,the very good step response being obtained for wc=1500.42Therefore,the control law for the electrical current,as it results from Eq. (22), is a PI one, with the next gains:42

At the next step,the following values were obtained for the coefficients for the speed PI controller,based on the data flow in the block diagrams in Figs. 6 and 7:42

and the value of the proportional gain for the P controller used in position loop is:42

According to the motor technical documentation, the used value for the torque constant was kt=0.024 Nm/A, for the motor moment of inertia, J=3.5×10-6Kg·m2, and for viscous friction coefficient, B=3×10-6N·m·s/rad.
In practice, the driving of a BLDC motor, equipped with three Hall-effect based sensors to have information related to the rotor position, is performed by using a general scheme as in Fig. 8.54The scheme includes an Insulated-Gate Bipolar Transistor(IGBT)driver and a three-phase inverter.The effective control is made by using Pulse Width Modulated (PWM)signals, which establish the average values of the driving coils voltages and currents. On the other way, based on SimPowerSystems toolbox blocks in Matlab, the Simulink model of the controlled BLDC motor can be organized as in Fig. 9.42
According to the model, by using the right values for the proportional and integral gains in the electrical current control loop of the motor, as are, for example, the previously calculated gains KPcand KIcfrom Eq.(23),will be generated a duty cycle of high frequency PWM signals which allows for proper control in the speed and position channels.
The next loop considered in motor control achieving is reserved to the motor speed; the proportional-integral speed controller provides a reference value for the electrical current,which is actually the input value for the current controller. In the same time,the sign of this reference value dictates the rotation sense of the motor rotor,as it is used in the elaboration of the commutation signals in the block ‘‘Commutation table”together with the signals received from the Hall-effect based sensors.The last control loop,the outermost one,is reserved to the control of the position, and implements a proportional control law.

Fig. 8 BLDC motor control using PWM.54

Fig. 9 Actuator control by using SimPowerSystems toolbox in MATLAB.42
Using the simulation scheme in Fig. 9, which implements the tuned controllers for all three loops, the results in Fig. 10 were obtained for a position step input. The left-hand side of the figure presents the desired (reference) and obtained positions for the linear actuation (expressed in mm), while the right-hand side of the figure shows a comparative graphical exposure of the following speed signals (expressed in rpm):(A) the reference speed, collected as the output from the position controller block, and (B) the obtained speed, calculated starting from the obtained linear position. At the next step,the tuned controllers were tested with a more complex input signal in the form of a repeated sequence signal, with positive and negative ramps and actuation limits between -3 and 3 mm. The results depicted in Fig. 11 were obtained. All numerical simulation results shown proper functioning of the obtained control scheme for the morphing actuator based on the BLDC motor, the used design approach providing a simplified method for tuning its control gains.
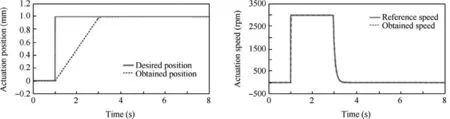
Fig. 10 Results obtained from numerical simulation for a position step input as desired position.

Fig. 11 Results obtained from numerical simulation for a repeated sequence input signal as desired position.
5. Bench testing of morphing wing control system
The developed experimental model for the deformable wing is tested both at the laboratory level,with no airflow,to evaluate the components integration and the whole system functioning,but also in the wind tunnel,in the presence of airflow,to evaluate its behavior and to validate the results predicted through numerical optimization from the aerodynamic point of view.
The control gains that were obtained were experimentally validated in bench tests for all of the four actuators used to morph the wing model. The whole bench testing operation was realized at E´ TS in the LARCASE laboratory.The architecture of the experimental testing system is presented in Fig. 12, and was developed by using a Real Time(RT)Target from National Instruments(NI).As can be easily observed,to have information related to the real values of the actuated distances (control feedback) for the morphing actuators four LVDT linear position sensors are used.
The bench test instrumentation is developed by using some programmable EPOS drives, produced by the Maxon Motor Company and dedicated for the BLDC motors integrated in the actuators, but also, by using the PXI technology from NI. Once performed the testing and validation of the control gains through numerical simulations, in order to develop the experimental model, it is necessary to be performed a conversion before programming them into the drives, according to the Maxon motors application notes.55The following equations show how the gains from SI units (used in Simulink)are converted to EPOS units.For the electrical current control it results:42
Fig. 12 Architecture of experimental testing system.

while, for the speed control:

and for the position control:

The flow of the design and bench testing of the control system can be summarized as in Fig. 13.
After the conversion and implementation of the IMC tuned gains into the EPOS drives,various actuation commands were tested for the four actuators, both independently and simultaneously.The purpose of the independent actuator control was to assess whether it meets the mechanical requirements to which it is subjected when the wing is morphed.
When the actuators were simultaneously tested, firstly has been evaluated the behavior of the integrated morphing system in all optimized flight cases,and then the behavior of the morphing skin under various limit cases, where some of actuators pulled the skin and others pushed it, starting from the reference airfoil position. Fig. 14 presents the control results for one actuator at a repeated step input signal as desired position.The first graphical window exposes the experimental obtained position versus the position obtained through numerical simulation and the required position, while the second graphical window shows the motor angular speed obtained during the experimental testing.
The graphical characteristics,drawn for position in the first window of Fig. 14, prove that the obtained mathematical and software models reflect well the behavior of the experimental system. Therefore, the variant with a full bridge drive for the BLDC motor, operating in the two-phase conduction mode,was a good choice for the mathematical modelling step.

Fig. 14 Bench test results for one actuator at a repeated step input signal as desired position.
A short analyze of the characteristics shows that the rise times for numerical and experimental responses are approximately the same, but a small time delay in the command execution appears in the experimental situation. Few factors can generate and influence independently and/or cumulated the values of these delays,but also the allures of the time responses for position and speed: (A) the inherent differences between the obtained linear model and the nonlinear behavior of the actuation system in various actuation configurations; (B) the complex behavior of the morphed flexible skin, which generates a variable and hard to predict load when it is actuated(the load has been considered constant in the numerical simulations); (C) the behavior of the hardware equipment interfacing the control system with the real actuator (noise, time delays, etc.).
An important role is played by the experimental flexible skin equipping the model because it was attached on all four sides of the wing, attachment which increased its rigidity; the rigid structure, as well as, the flexible skin were specifically designed to meet aeronautical industry requirements.The time delays can be easily correlated with the angular speed profile in the second graphical window of Fig. 14, observing that the speed transition from zero to the maximal value is made following various ramps with the slopes influenced by the changes in load.

Fig. 13 Flow of design and bench testing of the control system.
Viewed in the context of the morphing wing project general aim, i.e. to extend the laminar flow regions on the wing surface, and thus to reduce the drag over an operating range of flight conditions, the discussed time delays are practically insignificant, taking into account the duration of a flight.Besides these delays, a more important aspect which can be noticed analyzing the curves in Fig. 14 is that the controlled experimentally model does not have steady-state errors,which means that the designed control system meets the most important condition to obtain a good experimental reproducibility of the numerical optimized wing shapes. Therefore, the experimental testing results demonstrated adequate functioning of the controlled morphing wing model, and recommended its preparation for the next series of experimental tests in a wind tunnel.
6. Evaluation of morphing wing experimental model through wind tunnel testing
For an assessment of the aerodynamic benefits provided by the morphing technology, the project research team tested the developed experimental model in the presence of airflow, in the National Research Council of Canada subsonic wind tunnel. The performed tests aimed also at the validation of the numerical study performed by the aerodynamic team and at the evaluation of the integrated morphing wing system behavior in various situations simulating a real flight, with different incidence angles,Mach numbers,aileron deflection angles and with the inherent perturbations induced by the wind tunnel.Fig. 15 presents the placement of the morphable wing experimental model in the IAR-NRC wind tunnel testing room;the wing position was a vertical one, which means that the variation of the incidence angle has been obtained by rotating the model around a vertical axis. The wind tunnel testing was performed for 97 flight cases, which were generated by combining various values of the incidence angle (nineteen values,between -3° and +3°), Mach number (three values: 0.15,0.20 and 0.25) and aileron deflection angle (thirteen values,between -6° and +6°).
For an easiest interaction of the human operator with the experimental model a Graphic User Interface (GUI) has been conceived(see Fig.16);it allowed a safe testing and a complex evaluation of the experimental model in various situations.The GUI was organized to provide some functions, booth from the safety,but also from the testing needs points of view:emergency stop, mode selection (Manual, Flight case and Homing), flight case selection, real time displaying of the actuated distances by using the numerical indicators,real time plotting of the measured actuation distances and of the reference skin necessary actuation distances.
During all of the wind tunnel tests the Kulite sensors pressure data were real time processed to provide information related to the laminar-to-turbulent transition location; simultaneously with the control system survey based on the GUI,the Fast Fourier Transforms (FFT) for the acquired pressure data have been real time visualized on a parallel screen. Additionally, aiming at the evaluation of the laminar-to-turbulent transition location over the whole wing upper surface,not only on the Kulite sensors station, the Infra-Red (IR) thermography method was applied. Also, with the aim to get a further post-processing analyze, the Kulite data were acquired at 20 kHz rate for all of the tested flight cases, both for original(un-morphed) and optimized (morphed) airfoils.
Fig.17 exposes the results of the IR thermography for original and deformed airfoils in the flight case 19, generated for Ma=0.15, α=1.5° and δ=0°; the air flows from the left to the right, booth pictures being views from the leading edge side of the morphable wing model,similar with the second picture presented in Fig.15.For both airfoils the NRC team estimated the average transition line on the wing upper surface by using the gradient method; Fig. 17 shows that the transition location depends by the chord-wise position. In the current flight case, the estimation of the transition position for whole wing provided the mean values of approximately 49%(±2%) of the chord (49.26%(±2%)) for original airfoil, and 52%(±2%)of the chord(51.72%(±2%))for morphed airfoil,respectively. Also, on the span-wise station associated to the Kulite sensors (at 40% of the model span) the estimation of the transition position provided the values of 49.18% of the chord for original airfoil (somewhere between Kulite #13 and Kulite #14),and 52.08%of the chord for morphed airfoil(somewhere between Kulite #18 and Kulite #19). Therefore,the IR measurements revealed that, in this flow case, the use of the morphing technology produced an extension of the laminar region over the whole wing upper surface with a mean value of about 2.46% of the chord, while in the Kulites span-wise station the extension was approximately 2.90% of the wing chord.

Fig. 15 Positioning of morphable wing in the IAR-NRC wind tunnel testing room.

Fig. 16 Experimental model associated GUI.

Fig. 17 IR visualizations for Ma=0.15, α=1.5° and δ=0°airflow conditions (Case 19).
The post-processing analysis, starting from the recorded pressure data, provided information related to the transition point position in the Kulite span-wise station by using two mechanisms: (A) the evaluation of the STandard Deviations(STDs)for the data collected from each of the 32 pressure sensors to obtain a graphical representation of the pressure fluctuations in the boundary layer of the flow;(B)the analyze based on the Fast Fourier Transforms (FFT) for the Kulites recorded data on each pressure channel to evaluate the noise magnitude in the air flow over the morphable wing upper surface.
The using of the first mechanism for the previous analyzed case(Ma=0.15,α=1.5°and δ=0°airflow conditions)provided the plot diagrams exposed in Fig. 18, for both, original and deformed airfoils. According to that, the maximum value of the pressure data STD for original airfoil corresponds to the Kulite #14, and for the deformed airfoil to the Kulite #19. A big value for the pressure data STD on one pressure detection channel comparatively with the other channels suggests the presence of the turbulence influences in the acquired signal for that channel, which means that the turbulence started somewhere between the Kulite sensor associated with this channel and the previous Kulite sensor.
The second evaluation mechanism, based on the FFT decomposition, generated the graphics presented in Fig. 19,for un-morphed airfoil, and in Fig. 20, for morphed airfoil.If a turbulent airflow is present over a pressure sensor monitoring the flow on the morphable wing upper surface, then its associated FFT curve will be detached.For both mechanisms,the resolution for the laminar to turbulent transition position detection depends by the density of the sensors used to measure the pressure signals over the monitored surface. Because here have been used 32 pressure detection channels, which means a higher graphical data density, the FFT analyze was conducted step by step, depicting the associated curves for clusters of eight sensors counted successively beginning from the wing leading edge. Therefore, each of the Figs. 19 and 20 includes five graphical windows, the first four describing the FFT curves for these clusters of eight sensors, while, to have an image of the airflow on the whole Kulite station, the last one contains the FFT curves for all 32 detection channels.
As in the STD based analyze, the FFT results suggest that for the original airfoil the turbulent flow is present at the level of the pressure sensors#13 and#14(second and fifth graphical windows in Fig.19),and for the deformed airfoil its maximum influence is at the level of the pressure sensors #18 and #19(third and fifth graphical windows in Fig. 20).
It can be observed that all of the three techniques used to detect transition position provided similar results for the pressure sensors span-wise station both for original and morphed airfoils, validating in this way the IR thermography analyze of the flow performed for the whole wing. Also, for the great majority of the wind tunnel tested flight cases the research team of the project observed that the morphing technology improved the average position of the laminar to turbulent flow transition over the whole wing with more than 2.5% of the wing chord.

Fig. 18 Standard deviations of pressure data recorded in flow case 19 (Ma=0.15, α=1.5°, δ=0°).

Fig. 19 FFT results for original (un-morphed) airfoil at Ma=0.15, α=1.5°, and δ=0° (flow Case 19).
For the previous exposed flow case, the IR measurements proved that the morphed airfoil beneficiated by an expansion of the laminar region over the whole morphable wing upper surface with a mean value of about 2.46% of the chord, while in the Kulites span-wise station the extension was approximately 2.90% of the wing chord.
7. Conclusions

Fig. 20 FFT results for the morphed airfoil at Ma=0.15, α=1.5°, and δ=0° (flow Case 19).
This paper presented the control tuning, instrumentation and experimental testing and validation for a morphable wing experimental model actuated using four miniature BLDC motors. The four used actuators were similar, and were required to produce a direct linear actuation of the flexible upper surface of the wing, manufactured from composite materials with elastic properties. The positions of the four actuation points were determined starting from the aerodynamically optimized shapes obtained for the deformable wing through numerical simulation in various flow cases.The structure of each actuator includes a BLDC motor and a mechanical part which converts rotation movement into linear movement. Due to limited space and the high actuation force requirements imposed by our application, the actuators were in house manufactured using miniature BLDC motors from the Maxon Motor Company.
The tuning of the three control loops included in the actuator control system was achieved using the Internal Model Control (IMC) methodology. The first testing step included a numerical simulation,all results proving an adequate functioning of the obtained control scheme. Finally, the obtained control gains were validated in bench tests and wind tunnel tests experiments on all four morphing actuators incorporated by the morphable wing actuation mechanism. The experimental model was based on certain programmable EPOS drives,which were used for position control for the BLDC motors,and on the NI PXI technology.The bench testing results,with no aerodynamic load on the model, revealed a very good behavior of the controlled morphing wing model,recommending its preparation for the next series of experimental tests in a wind tunnel.
For an assessment of the aerodynamic benefits provided by the morphing technology, the project research team tested the developed experimental model in the presence of airflow,in the National Research Council of Canada subsonic wind tunnel.The performed testing actions aimed also at the validation of the numerical study performed by the aerodynamic team and at the evaluation of the integrated morphing wing system behavior in various situations simulating a real flight,with different incidence angles, Mach numbers, aileron deflection angles and with the inherent perturbations induced by the wind tunnel.
To estimate the laminar to turbulent transition location over the entire upper surface of the morphable wing the Infra-Red (IR) thermography method has been used. Also,to have information related to the transition point position in the Kulite span-wise station two mechanisms were applied:(A) the evaluation of the standard deviations (STDs) for the data collected from each of the 32 pressure sensors; (B) the Fast Fourier Transforms(FFT)decomposition of the acquired data on each pressure channel.
All of the three techniques used to detect transition position provided similar results for the pressure sensors span-wise station both for original and morphed airfoils, validating in this way the IR thermography analyze of the flow performed for the whole wing.
For the great majority of the wind tunnel tested flight cases the research team of the project observed that the morphing technology improved the average position of the laminar to turbulent flow transition over the whole wing with more than 2.5% of the wing chord. On the other way, the results presented in the paper for the flight case 19, generated for Ma=0.15, α=1.5° and δ=0°, shown that, according to the IR measurements, the morphed airfoil beneficiated by an expansion of the laminar region over the whole morphable wing upper surface with a mean value of about 2.46% of the chord, while in the Kulites span-wise station the extension was approximately 2.90% of the wing chord.
Acknowledgements
The authors would like to thank the Thales team for their support, with special thanks to Mr. Philippe MOLARET, Mr.Bernard BLOUIN and Mr. Xavier LOUIS, and the Bombardier Aerospace team - Mr. Patrick GERMAIN and Mr.Fassi KAFYEKE for their help and fruitful discussions. We would also like to thank Bombardier Aerospace, Thales, and the Consortium for Research and Innovation in Aerospace in Quebec (CRIAQ) and the National Sciences and Engineering Research Council (NSERC) for the funding received in connection with the CRIAQ MDO 505 project.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Reliability and reliability sensitivity analysis of structure by combining adaptive linked importance sampling and Kriging reliability method
- Aeroelastic dynamic response of elastic aircraft with consideration of two-dimensional discrete gust excitation
- Thermal damage analysis of aircraft composite laminate suffered from lightning swept stroke and arc propagation
- An aerospace bracket designed by thermo-elastic topology optimization and manufactured by additive manufacturing
- Applications of structural efficiency assessment method on structural-mechanical characteristics integrated design in aero-engines
- An energy-based coupling degradation propagation model and its application to aviation actuationsystem
