Reliability and reliability sensitivity analysis of structure by combining adaptive linked importance sampling and Kriging reliability method
2020-06-11FuchoLIUPengfeiWEIChngcongZHOUZhufengYUE
Fucho LIU, Pengfei WEI,b,*, Chngcong ZHOU, Zhufeng YUE
a School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an 710129, China
b Institute for Risk and Reliability, Leibniz Universita¨t Hannover, Callinstr. 34, Hannover, Germany
KEYWORDS Active learning Kriging model;Adaptive linked importance sampling;Reliability analysis;Sensitivity analysis;Small failure probability
Abstract The application of reliability analysis and reliability sensitivity analysis methods to complicated structures faces two main challenges: small failure probability (typical less than 10-5) and time-demanding mechanical models. This paper proposes an improved active learning surrogate model method,which combines the advantages of the classical Active Kriging-Monte Carlo Simulation (AK-MCS) procedure and the Adaptive Linked Importance Sampling (ALIS) procedure.The proposed procedure can,on the one hand,adaptively produce a series of intermediate sampling density approaching the quasi-optimal Importance Sampling(IS)density,on the other hand,adaptively generate a set of intermediate surrogate models approaching the true failure surface of the rare failure event. Then, the small failure probability and the corresponding reliability sensitivity indices are efficiently estimated by their IS estimators based on the quasi-optimal IS density and the surrogate models. Compared with the classical AK-MCS and Active Kriging - Importance Sampling (AK-IS) procedure, the proposed method neither need to build very large sample pool even when the failure probability is extremely small,nor need to estimate the Most Probable Points(MPPs),thus it is computationally more efficient and more applicable especially for problems with multiple MPPs.The effectiveness and engineering applicability of the proposed method are demonstrated by one numerical test example and two engineering applications.
1. Introduction
Reliability and reliability sensitivity analysis has proved to be an essential part in the design process of structures due to the existence of multi-source uncertainty, such as material performance dispersion and manufacture error.1-4Although nonprobabilistic models and imprecise probability models have both been applied for dealing with this type of problems,5-8the classical probability model is still the most attractive one due to its wide applicability,9thus the reliability and reliability sensitivity analysis problems subjected to probability model are concerned in this work.Typically,applying reliability analysis methods to a structure involves two main challenges.10First, the structure is well designed and the failure surface is far away from the distribution center of the input variables,meaning that the failure probability is very small. This kind of problem is ubiquitous in, e.g., aerospace engineering. Second, the mechanical models are commonly computationally expensive, making the available method impractical when the computational efficiency is concerned.
For assessing the small failure probability,the Monte Carlo Simulation (MCS)11is commonly inefficient. To reduce the computational costs and make the estimation accurate, a lot of improved numerical simulation methods have been developed, such as Importance Sampling (IS),12,13Subset Simulation (SS),14,15Line Sampling (LS),16,17Directional Sampling(DS)18,19and Adaptive Linked Importance Sampling(ALIS).20IS is widely used for its efficiency, but it generally does not work in high dimensions.21As shown by Katafygiotis and Zuev,the samples generated by the fixed Importance Sampling Density (ISD) cannot cover the important region of the high-dimensional failure domain.22To address this issue,Katafygiotis and Zuev20proposed the ALIS. This method introduces a family of intermediate distributions which converge to the most optimal sampling density,by which the samples in failure domain could be efficiently obtained. From this respect,SS could be regarded as a special case of ALIS,whose conditional distributions obtained from intermediate nested failure events correspond to the intermediate ISD of ALIS.Overall, these advanced numerical simulation methods mentioned above are more efficient than the crude MCS, but in most engineering applications,the computational costs are still unaccepted.
For time-demanding models, a first alternative for reliability analysis is the First Order Reliability Method(FORM)23or the Second Order Reliability Method (SORM).24The Most Probable Point (MPP) is required in these methods, based on which the first or higher order Taylor series expansion is implemented,and then the failure probability is assessed via estimating the statistic moments. When multiple MPPs exist or the derivatives of the limit state functions cannot be computed,these two methods commonly fail to estimate the failure probability without special treatment.25Compared with the above two methods, the surrogate model methods have attracted more attentions. These methods approximate the limit state functions with explicit or semi-explicit functional expressions(called surrogate models) based on strategic Design of Experiments(DoE),and then estimate the structural reliability based on the surrogate models. The commonly used surrogate models include response surface,26-29neural network,30support vector machine,31,32polynomial chaos expansion,33moving least square regression34and Kriging surrogate model.35,36Among these surrogate models, the Kriging surrogate model has attracted the most attention in the community of structural reliability due to its robustness and wide applicability. It presents several characteristics different from other metamodels.36First, Kriging is in fact an interpolation surrogate model,which means that the prediction of a training point is exactly the true response value of this point. Second, the error of the prediction at any new non-training point can be easily assessed by the conditional variance, which in turn, provides a flexible way for active training. The above characters of the Kriging surrogate model have motivated the development of the active learning method, which approximates the true failure surface adaptively by adding new training point that can improve the accuracy of failure probability estimation the most. The commonly used active learning functions include Ufunction,36H-function,37Expected Feasibility Function(EFF),35Least Improvement Function (LIF),38etc.
To deal with the time-demanding models with small failure probability, combining the numerical simulation methods and surrogate models has been a common practice. Echard et al.combined the active learning Kriging model and MCS to develop the AK-MCS method.36Based on the similar idea,the AK-IS method which combines Kriging with IS,10and the AK-MCMC which combines Kriging with SS,39have both been developed.However,as mentioned above,the application of AK-IS will be limited by the fixed ISD, and in some situations, the limit state function is too complicated to find the MPP and even there may be more than one MPP. To avoid these disadvantages, this work focuses on the combination of the active learning Kriging model and ALIS to introduce a more refined method referred to as AK-ALIS. This procedure combines the advantages of both ALIS and AK-IS procedures,which,on the one hand,adaptively produces a set intermediate sampling densities converging to the quasi-optimal IS density,and on the other hand,generates a set of surrogate models for intermediate failure events converging to the true failure surface.Thus,the proposed AK-ALIS procedure is actively learning in both the sampling density and failure surface, and it is shown to be more flexible and effective.
Another important task in the context of reliability is to estimate the Parametric Reliability Sensitivity (PRS)indices,40-43which are commonly defined as the partial derivatives of the failure probability w.r.t. the distribution parameters of model input variables, and reflects the effects of each parameter on the structure reliability. Based on the proposed AK-ALIS procedure, we also calculate the reliability sensitivity indices, and it is shown that no extra computational cost is introduced for estimating these indices.
The organization of this work is as follows. Section 2 reviews the basic concepts of reliability analysis and PRS,and Section 3 presents the review of some efficient reliability analysis methods. The introduction of the proposed reliability and reliability analysis estimation method is presented in Section 4. Section 5 provides one numerical example and two engineering examples. Finally, Section 6 presents the conclusions.
2. Problem state

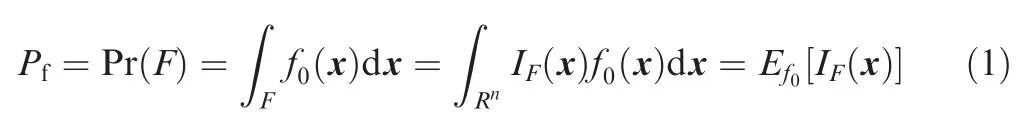
where IFis the indicator function which equals 1 if x ∈F, and equals 0 otherwise, and Ef0[·] indicates the expectation operator with respect to the density function f0(x ).
With the standard Monte Carlo simulation method,11Pfcan be estimated as an average of IFover a large number of samples of x:

For one distribution parameter θi,jof variable xi, the PRS index is defined as the partial derivative of Pfwith respect to θi,j. However, this type of PRS index depends also on the unit of the input variable. To avoid this disadvantage, Wu and Mohanty42introduced the normalized PRS index of θi,j:

The aim of this paper is to develop efficient active learning algorithm for estimating Pfand Tθi,j.
3. Reliability analysis
3.1. Importance sampling (IS)
Importance sampling is an efficient method in reliability assessment to reduce the Coefficient of Variation (CoV) of the MCS estimates. The basic idea behinds IS method is to replace the sampling density f0(x )with a well-designed density fz(x ),denoted as IS density,so as to generate more samples in the failure region. Thus the major challenge of the application of IS method is to specify the optimal sampling density fz(x )which can minimize the covs of estimates. The simplest way to generate an IS density is to move the sampling center to the MPP specified by FORM method. Then the probability of failure can be estimated as follows:

The IS estimator of the failure probability is then formulated as:

wfz(hx e)r.e
This method is widely used for its efficiency,but it is generally not applicable in high dimensions given the fact that the importance sampling density is fixed. Katafygiotis and Zuev have given a geometric interpretation of this phenomenon.22As shown by Katafygiotis and Zuev, the failure domain is much complex in high dimensions such that the samples generated by a fixed importance sampling density cannot cover the importance region of the failure domain. To avoid this disadvantage, Katafygiotis and Zuev introduced Adaptive Linked Importance Sampling (ALIS).20
3.2. Adaptive linked importance sampling (ALIS)
Unlike the IS that utilizes the fixed importance sampling density to directly generate the samples for the reliability analysis,the ALIS adaptively produce a set of intermediate importance sampling densities so as to approach the optimal IS density,thus the necessity of MPP and the limitation in high dimension can be avoided. This method is briefly reviewed as follows.
The probability density function f0(x ) and fz( x) in Eq. (4)can be expressed as follows:

where p0(x ) and pz(x ) are the non-normalized density functions that are known pointwise,C0∫and Czare the c∫orresponding normalizing constants equal toRnp0(x )dx andRnpz(x )dx respectively. Now, the estimation of failure probability in Eq.(4) can be reformulated as follows:

Since p0(x ) and pz(x ) are known pointwise, the estimation of failure probability can be transformed as the problem of estimating the ratio r=Cz/C0with the samples generated from fz(x ),20which can be derived as follows:

One potential problem is that if the supports of f0(x ) and fz(x ) are not nested, there is no way to estimate r by sampling from f0(x ).20Indeed, this can be easily worked up based on bridge sampling,44-46and the estimate for Cz/C0can be replaced by a ratio of estimation for Cbridge/C0and Cbridge/Cz, where Cbridgeis the normalizing constant for the bridge distribution pbridge(x ).


Fig. 1 Illustration of bridge distribution.

The estimation of Eq.(8)is sufficiently accurate if f0(x )and will be very large.20
To improve the accuracy, a sequence of intermediate nonnormalized density functions pj(x ),j=0,1,...,z, are introduced.p0(x )and pz(x )are the first and last samplingfunctions respectively. Similarly, le∫t fj(x )=pj(x )/Cjdenote the intermediate PDF, where Cj=Rnpj(x )dx represents the corresponding normalizing constant. Then, the ratio r=Cz/C0can be estimated as follows:

3.3. Active learning and Kriging-based importance sampling(AK-IS)

Fig.2 Illustration of the implementation procedure of the ALIS.
AK-IS is based on the active learning Kriging model and IS.10Samples are generated centered on one MPP, which is obtained from FORM approximation. Then active learning Kriging model is constructed to simulate the samples population. The application of Kriging model avoids the calculation of performance function at each point, and the accuracy of Kriging model prediction is constantly improved with the active learning functions. The usually used learning function is U-function, which is defined so that the probability that the classification of Kriging mean is accurately determined can be obtained by φ(U ( x )),where φ(·)is the cumulative density function of a standard normal distribution.Obviously,the larger the value of U(x ),the lower the probability of making a wrong classification of Kriging mean. The best sample added to DoE will be selected as the one with the minimum value of U(x ) to make an expected improvement on the Kriging model. Unlike other Kriging-based reliability methods that select the best new sample using an optimization method with the extra computational effort,the value of U(x )depending on the Kriging mean and variance can be regarded as a byproduct of the analysis process. With the new sample added to DoE,the Kriging model will be updated with an improvement of accuracy. This repeat will stop until the minimum value of U(x )is no longer smaller than one constant,which is generally selected as 2, i.e. the probability of making a wrong classification of Kriging mean is 0.023.47
Just as mentioned in Section 3.1, despite the efficiency of AK-IS, it is generally not applicable in high dimensions given the fact that the importance sampling density is fixed. In high dimensions, the failure domain is so complex that the samples generated by a fixed importance sampling density cannot cover the importance region of failure domain.To overcome this disadvantage, this paper introduces a new method called AKALIS by combining the active learning Kriging model with ALIS, which is detailed in the next section.
4. The AK-ALIS procedure
The basic idea of AK-ALIS is, instead of using a fixed importance sampling density as done in AK-IS, to introduce a sequence of intermediate distributions to converge to the quasi-optimal IS density. Also, the Kriging model will be updated iteratively as the new sample population is generated.The flowchart of the AK-ALIS procedure is shown in Fig. 3,and the specific procedure is described as follows:
Step 1. Selection of the intermediate distributions. A sequence of intermediate distributions fj(x ),j=0,1,...,z is selected, and one can refer to Appendix for details.
Step 2. Generation of sample population and selection of initial DoE. Let i=0, and a sample population P is generated from fi( x), i.e. the initial probability density function f0(x ). The number of samples is denoted as N. Then, the initial DoE consists of N0samples randomly selected from the sample population P. All the N0samples in DoE are evaluated with the limit state function.
Step 3. Train Kriging model. In this stage, the Kriging model is constructed using the Kriging toolbox DACE.48Step 4. Estimation of U value. The Kriging prediction is estimated at each of the N input samples. And the Kriging mean and variance are denoted asandrespectively,where j=1,2,...,N Then we can get the U value for each point by the formula as follows:

Step 5. Stopping criterion of the active learning. The function φ(U (xj)) represents the probability that the classification of Kriging mean at point xjis accurately determined.The point with the minimum U value, i.e. min U, has the maximum probability of leading to a wrong classification of Kriging mean.In this paper,the stop criterion is defined as the min U is not less than 2,which means the probability of classifying the Kriging mean accurately is at least 97.7%for all the samples.

Fig. 3 Flowchart of the AK-ALIS procedure.
Step 6.Add a new best sample to DoE.If the stop criterion in Step 4 is not satisfied. The Kriging model should be updated by enriching the DoE.Given the fact that the Kriging is an exact interpolation method, it is easy to find that the new best sample added to DoE is the one with the highest probability of making a wrong classification of Kriging mean, i.e. the min U. Add this point to DoE, let N0= N0+ 1, and then return to Step 3.
Step 7. Identify the number of samples lying in the failure domain.If the stop criterion in Step 5 is satisfied,the active learning stops and the Kriging model is considered as accurate in a high confidence level.Then,the number Nfof samples in failure domain can be estimated using Kriging model.Step 8.Generate a new samples population.If Nfis smaller than N/2, the samples in failure domain are not enough to accurately assess the ratio rj=Cj/Cj-1. Then,let i=i+1,and a new samples population following intermediate distribution fi(x ) will be generated with MH or MM algorithm, and the procedure goes back to Step 4.
Step 9. Estimation of the failure probability. If Nfis larger than N/2, the failure probability and reliability sensitivity analysis indices will be estimated. And, the AK-ALIS procedure stops.




5. Test examples
5.1. A numerical example
The limit state function is given as follows:

where x1and x2follow standard normal distribution independently.
Crude MCS, AK-ALIS+H and AK-ALIS+U are implemented to estimate the failure probability and the PRS indices. The estimation results of crude MCS procedure is defined as the reference value with 5×107samples.This number of samples is selected to make the coefficients of variation of the estimation results close to 5%.Both AK-ALIS+H and AK-ALIS+U are performed with 2000 samples, among which 20 samples are selected as the initial DoE.
As shown in Table 1, the reliability analysis results estimated by the AK-ALIS+U and AK-ALIS+H match well with that assessed by the crude MCS.The probabilities of failure obtained from these three methods are accurate enough,since the covs are all less than 5%.The total number of limit state function calls in AK-ALIS+U and AK-ALIS+H are 36 and 38 respectively,while that in crude MCS procedure is 5×107.However,in terms of computational time,the MCS preforms well with 18.6 s consumed,while AK-ALIS+U and AK-ALIS+H require 77.2 s and 91.1 s respectively. It is not hard to understand that despite the large number of limit state function calls, the simple numerical example could be easily handled by a computer with strong computing capability.Conversely, no matter how simple the example is, the AKALIS should perform its intrinsic procedure, which is more complex than a simple numerical example.
As shown in Table 1,the PRS indices are well estimated by all the three methods,and the sensitivity analysis results match well. From Table 1, the importance ranking of the standard deviation of these two input variables is reported as Tσ,2
5.2. A ten-bar structure
A ten-bar structure,as shown in Fig.4,is adapted from49with six random input variables.All the ten bars have the same sectional area and length,denoted as A and L,respectively.Three point loads Pi(i =1,2,3) apply on the ten-bar structure, as shown in Fig. 4. And E represents the elastic modulus of the ten bars. All the six random input variables obey normal distribution with the distribution parameters shown in Table 2.Let Δ denote the vertical displacement of node 3,and the limit state function is expressed as g=0.0044-Δ.
MCS, AK-ALIS+U and AK-ALIS+H are implemented to assess the failure probability and PRS in this application.Due to the low failure probability,5×107samples are simulated in the crude MCS procedure to make sure the estimated results are accurate enough. Besides, 100 samples are used as the initial DoE in both AK-ALIS+U and AKALIS+H, and 2000 samples are generated from the original PDF. Also, due to the complexity of limit state function, the AK-IS is not suitable with the difficulty to find the most probable point.
As shown in Table 3, the estimated failure probabilities from AK-ALIS+U and AK-ALIS+H are very close to that from MCS with 175 and 159 limit state function calls respectively, which are much less than MCS. Also, due to the extremely complex limit state function, 5×107calls required in MCS consumes 406.7 s to assess the failure probability and PRS indices,while AK-ALIS+U and AK-ALIS+H require 303.1 s and 332.5 s respectively. From this application, we could find that when the limit state function is extremely complicate and the failure probability is very low, the proposed AK-ALIS method is more efficient than MCS due to the less limit state function calls and a smaller samples size.

Fig. 4 A ten-bar structure.

Table 1 Reliability and sensitivity analysis results of the numerical example.

Table 2 The distribution parameters of the basic random variables for Example 3.

Table 3 Reliability results of the ten-bar structure.

Table 4 Sensitivity analysis results of the ten-bar structure.
As shown from Table 4, all the three methods applied in this application accurately estimate the PRS indices of these six inputs except P3, as its PRS indices are much less. From the second row of Table 4,the importance ranking of the mean of the six input variables is reported as μA≈μE>μL>μP1>μP2>μP3. The PRS indices of μA, μE,μp3are negative, implying that reducing the values of these three parameters,the failure probability will increase.It is easy to find that μAand μEhave a more negative effects on failure probability than μp3,while μLhas the most positive effects.The same ranking can be generated from the fourth row of Table 3.As for the standard variance, the importance ranking is σA>σE>σL>σP1>σP2>σP3, which is similar to that of the mean.It is obvious that σAand σEhave a significant impact on the failure probability.
5.3. An aircraft landing gear
An aircraft landing gear modeled by Adams is shown in Fig.5.Considering the design mistakes, the friction coefficients μA,μB,μC,μD,μEat points A, B, C, D, E are parameterized respectively. Also the coordinate of the connection point F between pull rod and fuselage need to be parameterized, i.e.LX,LY,LZ, because the installation error will affect the direction of the motion of actuator cylinder. The friction between airplane wheel and ground is denoted as f, and the maximum value of thrust of hydraulic cylinder piston is denoted as Fmax.All the ten random variables follow normal distribution, and the distribution parameters are shown in Table 5.
Let function Fmaxrepresent the maximum load of the landing gear. When the load of the landing gear exceeds the maximum value of thrust of hydraulic cylinder piston Fmax, the landing gear fails. Thus, the limit state function is given as:


Fig. 5 Dynamic simulation model of landing gear.
Considering that one run of this dynamic simulation model consumes 45 s to get the response value, the crude MCS,assuming 1×106samples are simulated, requires 4.5×107s(more than one year)to perform the reliability analysis,which is obviously unaffordable. Besides, due to the absence of analytical response function, it is hard to find the MPP to implement AK-IS. Therefore, AK-MCS+U, AK-ALIS+U and AK-ALIS+H are applied to solve this problem.
For each method, the DoE consists of 80 samples initially to construct the Kriging model.The size of sample population is 1×106in AK-MCS, while that is 2000 for both AK-ALIS+U and AK-ALIS+H.As shown in Table 6,the estimation results of failure probability obtained by these three procedures are close, with 190, 119 and 182 undercarriage model calls respectively. In term of the computational time, 22531 s required in AK-MCS is much more than that in AK-ALIS.It is easy to understand by the fact that the size of sample population in AK-MCS is much larger than that in AK-ALIS,thus AK-MCS has to consume more time to find the best new point added to the DoE than AK-ALIS.
It is shown in Table 7, if the values of the PRS results are small, the corresponding covs will be large, i.e. the results of PRS are not accurate. Thus, the AK-ALIS should be further investigated to enhance the accuracy of the PRS estimation results with small values. Although some PRS estimations are not precise, the importance ranking of the mean of the ten input variables is still obtained as μX7> μX8>μX6>μX9≈μX1≈μX2≈μX3≈μX4≈μX5≈μX10. It is shown that μX7has the most negative effect on the failure probability,while μX8has the most positive effect.The importance rankingof standard variance is σX7>σX8>σX6>σX3>σX4>σX1≈σX2≈σX5≈σX10≈σX9, indicating that, by reducing a small value of the SDs of the ten input variables, σX7leads to the most reduction on failure probability, while σX10makes the failure probability increase.

Table 5 Distribution parametric of the ten input variables of the aircraft undercarriage mechanism.
6. Conclusions
This paper develops an efficient and easily implementable method(AK-ALIS)for assessing the reliability and parametric reliability sensitivity.This method combines the active Kriging model and ALIS, and can be regarded as a generalization of the recently developed AK-MCMC method.50The active learning functions makes the construction of Kriging model efficient with the least number of training samples, and the Kriging model avoids the run of the initial time-demanding computational model of complex structures. Also, the construction of Kriging model is much easy benefited from the standard Kriging toolboxes. Unlike AK-IS that bases on a most probable failure point to construct an fixed Important Sampling Density (ISD) function, the AK-ALIS produces a set intermediate sampling densities converging to the quasioptimal IS density. The main advantage of AK-ALIS over AK-IS is that the AK-ALIS is more suitable for the highdimensional situation where AK-IS cannot be implemented due to the difficulty to select a fixed ISD to generate the samples covering the important region of failure domain. Thus,theoretically, the proposed method have unique advantage especially when multiple MPP exists or the behavior of the limit state function is too complex to correctly find the MPP.
The AK-ALIS is proposed to deal with the reliability analysis of complex structures with small failure probability and time-demanding computational models. The small failure probability means a large number of limit state function calls required in the crude MCS,and leads to an unaffordable computational cost when the computational model is time-demanding. However, as pointed out in Section 5.1, when applied in the simple numerical example, the crude MCS is more applicable than the proposed method.Although we have assumed that the input variables are characterized by precise probability models,the proposed method can also be extended for situations with multi-source uncertainty(e.g.,randomness,incompleteness and imprecision), e.g., based on our newly developed non-intrusive imprecise stochastic simulation method.6,39

Table 6 Reliability results of landing gear.

Table 7 Sensitivity analysis results of landing gear.
Acknowledgement
This work is supported by National Natural Science Foundation of China (Nos. 51905430, 51608446). Also, the Fundamental Research Fund for Central Universities (No.3102018zy011) is gratefully acknowledged. The second author would also like to acknowledge the supports of Alexander von Humboldt Foundation of Germany and the Top International University Visiting Program for Outstanding Young scholars of Northwestern Polytechnical University.
Appendix A. Proposed intermediate sampling distributions
In Ref. 20, two families of intermediate sampling distribution are proposed for ALIS, which could be further applied in AK-ALIS.
First, a limit state function is defined as follows:

The failure domain is defined as the area where φ (x )is negative. Then, the following two sequences of non-normalized intermediate sampling distributions are defined:

where α belongs in the ray α ∈0,+∞[ ].
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Aeroelastic dynamic response of elastic aircraft with consideration of two-dimensional discrete gust excitation
- Thermal damage analysis of aircraft composite laminate suffered from lightning swept stroke and arc propagation
- An aerospace bracket designed by thermo-elastic topology optimization and manufactured by additive manufacturing
- Applications of structural efficiency assessment method on structural-mechanical characteristics integrated design in aero-engines
- An energy-based coupling degradation propagation model and its application to aviation actuationsystem
- Model-driven degradation modeling approaches:Investigation and review
