空气导热系数和孔隙形状对多孔绝热材料相对导热系数的影响
2020-06-10邱潇薇汪晓雪王小见
邱潇薇,汪晓雪,王小见
(兰州交通大学,甘肃兰州 730070)
引言
多孔材料以往被广泛地应用于传热传质装置,如热交换器和保温材料等[1]。当前,多孔材料也被应用于绝热,导热系数成为一个关键的性能,其数值须小于0.15 W·m-1·K-1。许多研究者通过实验和理论方法研究了多孔材料的有效导热系数。张安等[2]基于Lockheed模型探究了多层绝热的实验机理。韩亚芬[3]在纳米复合隔热材料特性方面研究了孔隙大小对隔热材料的影响。Babaei等[4]利用分子模拟方法研究了孔径和形状对多孔材料导热性能的影响,研究的参数包括孔隙体积、孔隙形状、导热系数。
目前关于气体导热系数对多孔绝热材料(以下亦简称“多孔材料”)导热性能影响的研究相对较少。本文通过数值实验,探究五种孔隙形状下不同导热系数的空气对多孔材料绝热性能,即多孔材料相对导热系数的影响。细胞模型选择由微孔和基质材料组成的微胞。采用三维热传导模型模拟孔隙中的气体与基底材料之间的传热。
1 实验原理
1.1 细胞模型的构建
为了简化数值模型的计算,考虑了基底材料中由微孔组成的三维单元。该模型体积要足够小,有利于计算,但同时也要能够代表多孔材料的周期部分。据此,选择单个细胞模型的体积为0.002 m3。考虑五种孔隙形状:等边三角形、椭圆形、菱形、T形和I 形,并为它们各自定义尺寸。表1所示为单个细胞中随机分布的孔隙及其形状和尺寸。孔隙的位置和姿态角坐标(x0, y0, z0)可以由孔之间的中心、取向角β0、主要的y轴方向和热流方向来确定。本文开发了一种使细胞内孔的位置自动生成和使取向角随机分布的计算机程序。首先,确定孔隙中心位置,设坐标(x0, y0, z0)表示孔隙中心位置。其次,设Lx、Ly、Lz分别为细胞的长度、宽度和高度,如图1所示,其中T形孔隙分布于其中。然后,计算机生成一个随机数rx(0<rx<1)。x0被取为rx和Lx的乘积。同理得到y0和
1.2 热传导方程及边界条件
对于三维模型,热量在基体中的传导应满足方程
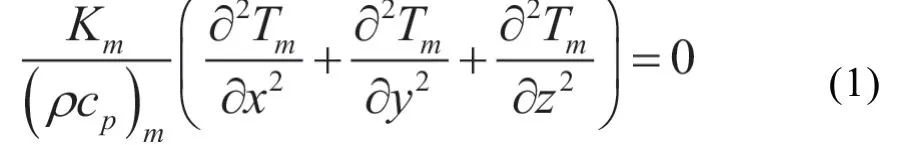
其中,T代表温度,下标m代表基材,Km为基材的导热系数。Km被设置为0.104 W·m-1·K-1,与石棉相同。ρ、cp分别代表基材的密度和等压比热容。
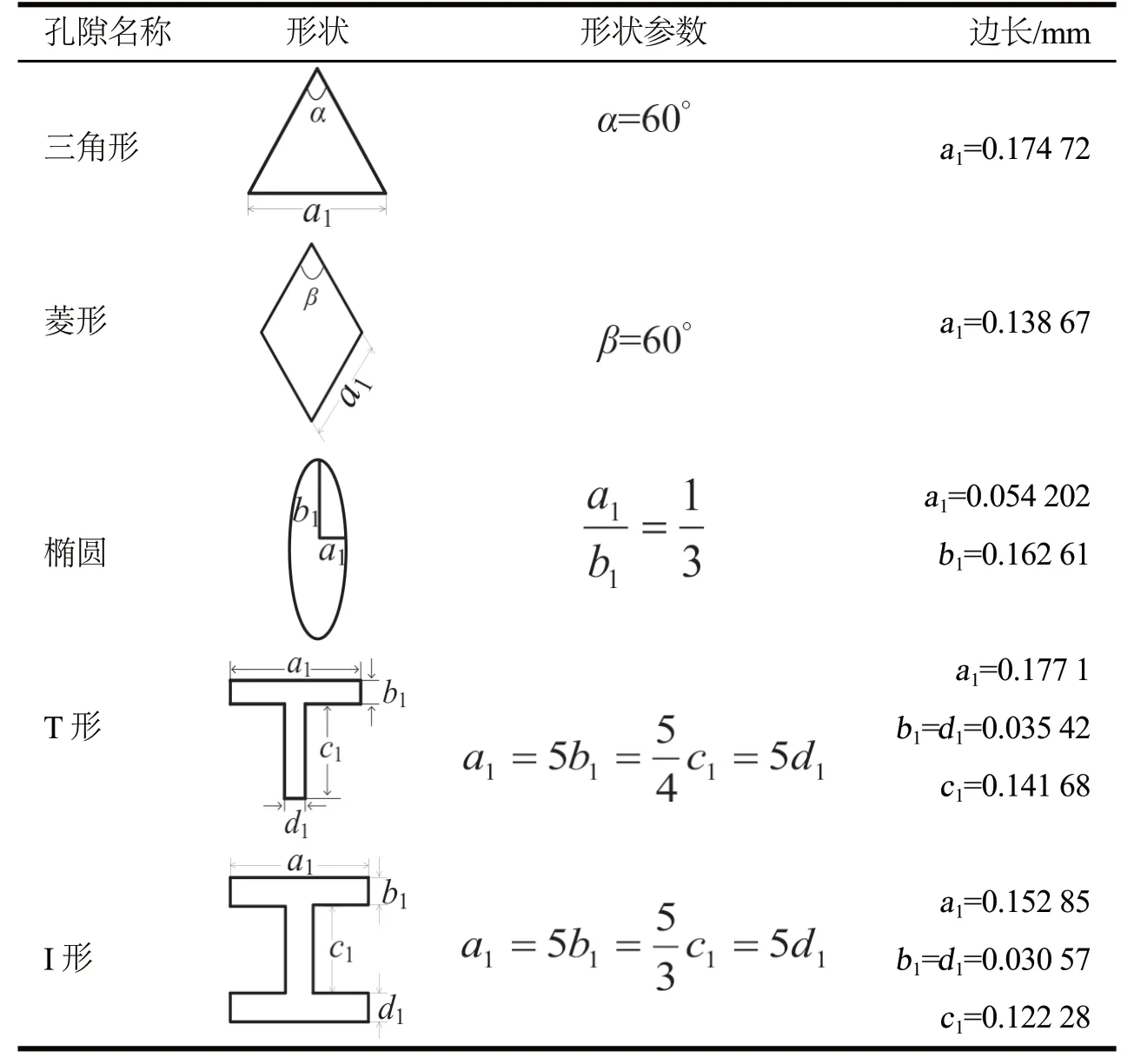
表1 单个细胞中随机分布的孔隙的形状和尺寸
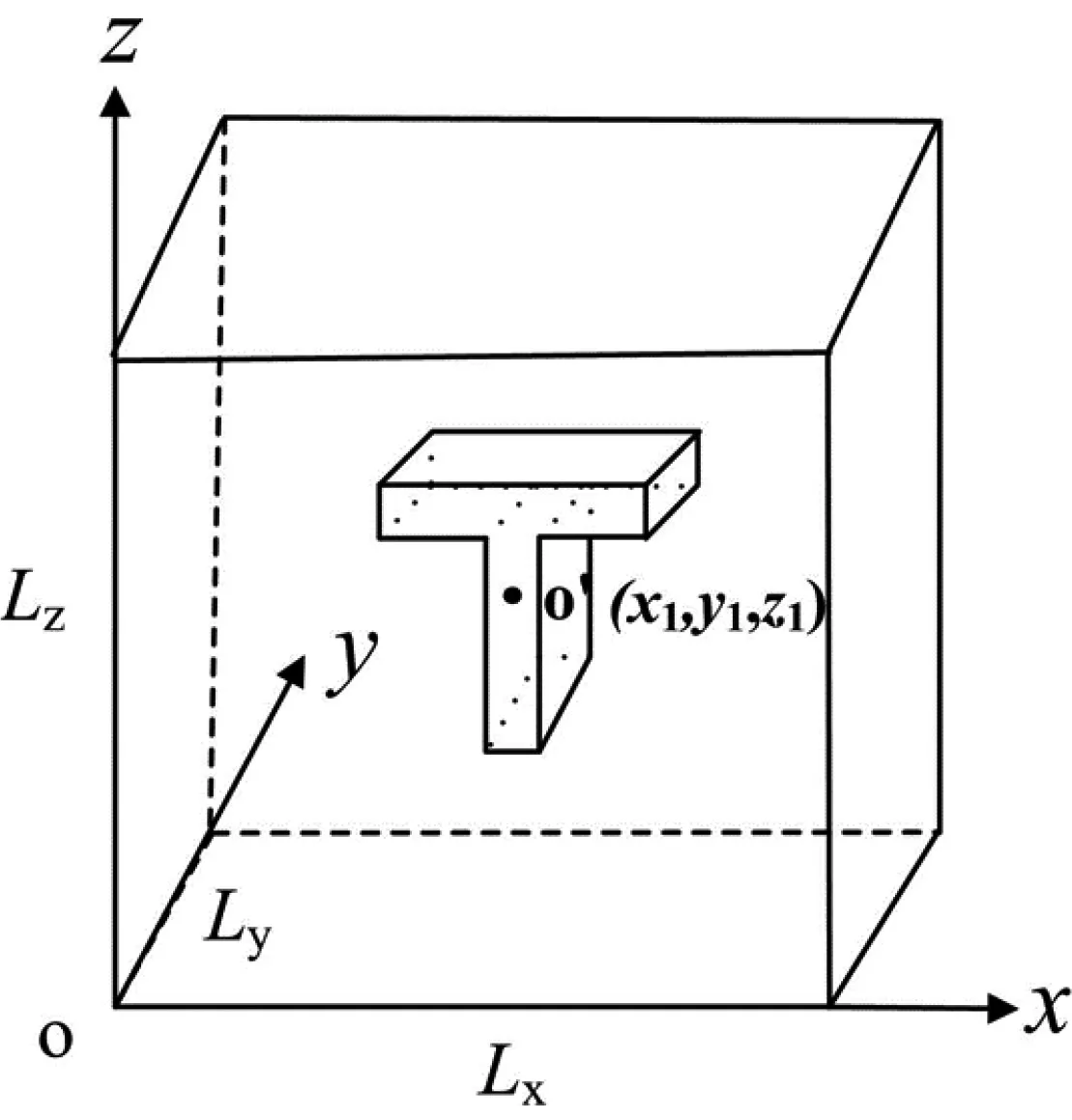
图1 在细胞尺寸及其中分布的T形孔隙
同理,热量在基体中的传导应满足方程
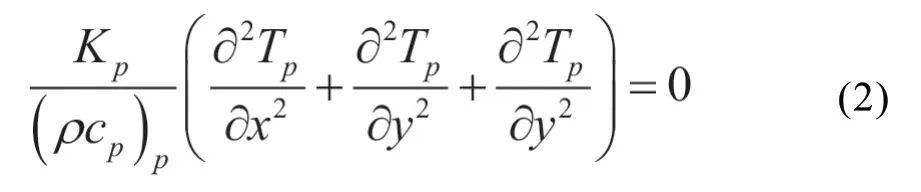
其中,下标p代表孔隙。Kp为气孔的导热系数,数值计算中取0.023 W·m-1·K-1,与空气相同。
细胞模型的上表面满足第二类经典边界条件

其中,q 为均匀施加于模型上表面的热流,数值计算中取1 000 W·m-2,n是模型的法向向量。
细胞模型的下表面满足第三类经典边界条件
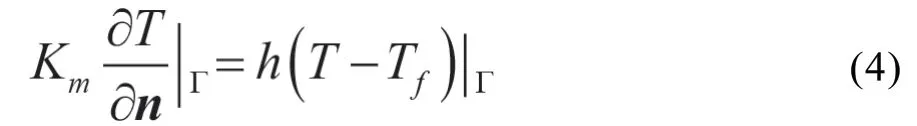
其中,对流传热系数h和环境温度Tf为常数,计算中h设定为20 W·m-2·K-1,Tf设定为300 K。
细胞模型的其他四个表面为绝热边界条件,即

数值计算最先要做到的是模拟多孔材料的热流流动状况,得到具体的热流值与相应的温度梯度。然后,以此为基础,计算多孔材料的有效导热系数。本文所选择的边界条件与导热系数的实际测量条件是一致的。
1.3 共轭热传导边界条件

在多孔绝热材料中,基材与导热填料接触面上的边界温度值相等,即二者处于一种共轭状态,接触面满足连续性边界条件,可表示为其中,下标interface表示基材与气体之间的接触面。当数学模型的温度场被确定后,模型沿y轴方向的有效导热系数就可以写作

1.4 控制方程的求解
通过有限差分技术求解基材与空气满足的共轭热传导方程,即式(1)~(7)。首先采用有限体积法对模型进行离散化,然后利用中心差分格式对离散化方程进行求解[5]。具体的计算步骤可以概括为:
(1)假设空气和基材的初始温度值;
(2)求解式(1),得到基底材料的内部温度场,再将气孔界面的温度值设定为基材边界上的温度值;
(3)求解式(2),获得空气的温度场,将步骤(2)计算得到的界面基材的温度值设定为与其接触的气体边界上的温度;
(4)回到步骤(2),直到计算获得的基材与空气的新温度值与旧温度值收敛为止。
至此,描述导热材料导热机理的共轭热传导方程求解完成。
2 结果与讨论
基体的导热系数是0.104 W·m-1·K-1,假设空气的导热系数的取值范围为0~0.104 W·m-1·K-1,将这一区间平均分成16份,在靠近空气的导热系数0.023 W·m-1·K-1附近,采用更加密集的离散方式,得到一组数据。图2所示为不同孔隙形状的多孔材料在不同空气导热系数下的相对导热系数。五种孔隙形状下的孔隙含量均为10%。可见,无论孔隙排列如何,多孔材料的相对导热系数随空气导热系数的增大而增大。但是,各自的增长速率是不同的。I形孔隙的增长速率最大,其次是菱形、三角形和T形孔隙,椭圆孔隙的增长速率最小。当空气导热系数为0.104 W·m-1·K-1时,五种孔隙形状下材料的相对导热系数增长趋势逐渐稳定。
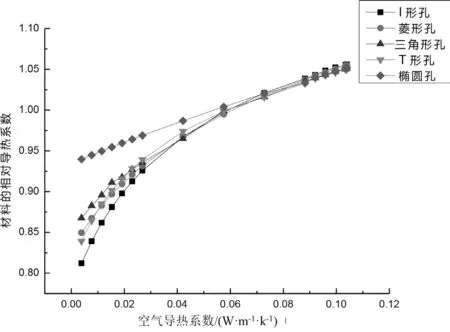
图2 不同孔隙形状的多孔材料在不同空气导热系数下的相对导热系数
图3所示为不同孔隙形状的多孔材料在不同孔隙含量Vf下的相对导热系数。在五种孔隙结构中,材料的相对导热系数随孔隙含量的增加而降低,与孔隙形状无关。数据来源于模态,孔隙含量从2%(N=10)增加到20%(N=100)。可见,无论孔隙形状如何,材料的相对导热系数总是随孔隙含量线性下降。然而,下降的程度是不同的。I形孔隙情形的下降速率最大,T形、三角形、菱形孔隙情形次之,椭圆孔隙情形的下降速率最小,即材料的导热系数降低的顺序为:I形、 T形、菱形、三角形、椭圆形。随着孔隙含量的增加,各种形状孔隙之间的数据差异越来越明显。在相同孔隙含量5%(N=25)时,I形孔隙与椭圆孔隙的差异不显著。而在相同孔隙含量10%(N=50)时,I形孔隙与椭圆孔隙的差异为3%左右。进一步地,在相同孔隙含量20%(N=100)时,二者差异大于9%。这种差异是由孔隙的形状导致的,这对多孔材料的相对导热系数有实质性的影响。由于空气的热阻远大于基底材料,所以基底材料中的等温线会发生变形并被空气封闭。气孔起阻碍作用,使热通量通过气孔受到延迟,热通量更倾向于在基底材料中绕过障碍物流动,这就类似于管道中的海绵,阻碍了流体在上游或下游的流动。垂直于流动方向形成的有效接触面积是影响流体流动的主要因素。质量流量随垂直接触面积的增大而明显减小。“海绵”沿流动方向的长度对流体流动的影响较小,在流体流动障碍中起着次要的作用。I形孔在上、下游的有效接触面积较大,沿热通量方向的热阻路径较长。椭圆孔的热阻路径较长,但在各种形状的孔隙中,垂直于热流方向的有效接触面积最小,因此隔热性能最差。
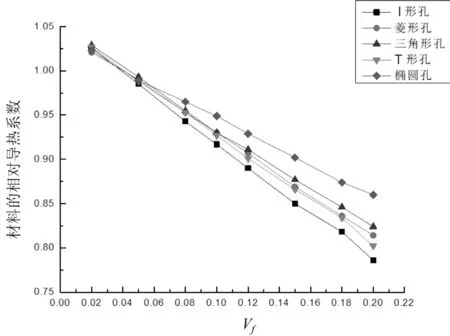
图3 不同孔隙形状的多孔材料在不同孔隙含量下的相对导热系数
3 结论
(1)多孔绝热材料的相对导热系数随着空气导热系数的增大而增大。
(2)当孔隙垂直于有效接触面积较大的热通量方向时,绝热性能最好。I形孔隙和T形孔隙有较大的有效接触面积,因此是降低绝热材料相对导热系数的最佳形状。
