悬浮态上皮细胞粘附的力学−化学耦合模型及数值模拟1)

冯世亮 周吕文 吕守芹†, 龙 勉†,

∗(宁波大学机械工程与力学学院,浙江宁波 315211)

†(中国科学院力学研究所生物力学与生物工程中心、中国科学院微重力重点实验室,工程化构建与力学生物学北京市重点实验室,北京 100190)

∗∗(中国科学院大学工程科学学院,北京 100049)

引言

上皮细胞(epithelial cells)彼此借助粘着连接(adherens junctions,AJs)形成连续上皮组织,由此发挥屏障、增殖调控等生理功能[1-2].上皮性钙粘附蛋白(Ecadherin,E-cad)作为一种跨膜蛋白,是调控AJs 形成的核心分子机制[3].一方面,E-cad 胞外结构域在Ca2+参与下,在胞间或同一细胞表面分别形成反式/顺式二聚体(trans-/cis-dimerization)[4],其胞质结构域则借助α,β 连环蛋白(α-,β-catenin)与肌动蛋白(F-actin)锚定[5]; 另一方面,胞间E-cad 成键引起Rac,Cdc42等Rho 家族小G 蛋白(Rho GTPase)激活[6],进而激活下游F-actin 结合蛋白(例如:Arp2/3,myosin-II,αactinin),调控肌球蛋白皮层(actomyosin cortex) 动态重组[7-9],由此将更多E-cad 募集至细胞接触区域,促使AJs 成熟[10].

近年来,随着体外重构(in vitroreconstitution)、活细胞成像等实验手段的广泛应用,研究者愈渐认识到皮层张力对于AJs 建成起整合性调控作用.Murrell等[11]将F-actin 积簇于脂质双层膜表面,再加入αactinin、myosin-II,由此可体外重构出actomyosin 皮层结构; 该实验借助改变F-actin 结合蛋白的密度控制皮层流变属性,通过检测F-actin 持续长度论证了Factin 屈曲及皮层松散结构可有效增强收缩应变.Wu等[12]对AJs 上粘着小带(zonula adherens,ZA)及侧边区域(lateral junctions) 进行激光烧灼,观测到前者回缩速率明显高于后者,说明ZA 区域维持着较高张力.Leerberg 等[9]将myosin 常规轻链基因(MRLCDD)转入Caco-2 细胞,使之表达myosin-II 磷酸化突变体以提升皮层张力,最终通过靶向实验验证了以α-catenin 受力打开VH2 结构域、从而募集vinculin 为主体的张力敏感型F-actin 聚合机制.Engl 等[13]将悬浮态S-180 细胞置入非粘附微井(microwell)之中,采取3D 成像观测细胞接触区域E-cad 募集,同时以Factin 解聚/稳定试剂(Latrunculin/Jasplakinolide) 处理细胞进行对照组实验; 观测到两类经处理细胞均呈现低张力状态,Jasplakinolide 对照组依然发生E-cad局部募集,说明张力通过降低F-actin 解聚速率调控E-cad.

综合上述实验,E-cad 胞间成键使细胞皮层局部张力增强,进而降低F-actin 解聚速率(亦或提高局部F-actin 聚合速率).考虑到F-actin 局部积聚能锚定更多E-cad,那么由“E-cad →张力→F-actin” 力学反馈回路所展现出的时空效应是否驱动了E-cad 局部积聚,进而调控AJs 形成动力学? 为此,本文构建了悬浮态上皮细胞粘附的力学−化学耦合模型,并采用格子Boltzmann−粒子(LBP)法开展数值模拟.模拟获得了悬浮态细胞相互挤压时的E-cad,F-actin 等分子时空调控特征并与Chu 等[14]实验对比,继而探讨了细胞局部力学属性、细胞间挤压程度对于AJs 的调控作用.

1 模型和方法

整体计算模型如图1(a) 所示.考虑细胞为环状结构,圆环代表细胞膜(指质膜及皮层紧密贴合体),内部为胞质区域,忽略细胞核等胞内细胞器;将细胞膜划分为非接触及接触区域,前者直接设定为由黏壶与弹簧并联的黏弹性单元,后者需额外考察细胞间相互作用.为考察分子沿可变形的细胞膜输运引入了自适应性D1Q3 单元,其长度与力学单元动态匹配;胞质内分子浓度均一,可由质量守恒定律直接获得.图1(b)展示皮层张力调控F-actin 解聚,而F-actin通过锚定E-cad 参与级联转导,由此循环往复构成了力学反馈回路.图1(c)展示采用马达−离合器(motorclutch)机制[15]考察细胞在相互接触区的力学作用.整体数学模型由3 个模块构成:细胞力学模块、Ecad/E-cad∗调控模块(* 号表明已与F-actin 锚定) 及F-actin 聚合/解聚模块.各模块的基本假设及控制方程如下.

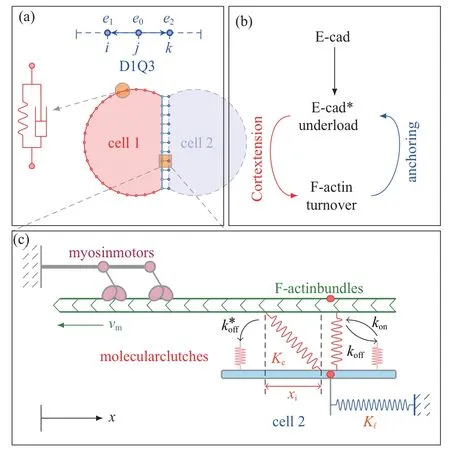
图1 (a)细胞离散模型.黏弹性单元与D1Q3 单元(1 维LBM 单元,包含3 个速度分量)动态匹配.(b)力学反馈回路示意图.(c)马达−离合器机制[15]Fig.1 (a)Discrete cell model.Each visco-elastic element is co-localized with a D1Q3 element(a)1D LBM element with 3 discrete velocity components).(b)Schematic of mechanical feedback loop.(c)Motor-clutch mechanism [15]

1.1 细胞力学模块

考察悬浮态上皮细胞具有均匀的力学属性,离散细胞模型上任意单元节点i的受力满足以下平衡微分方程

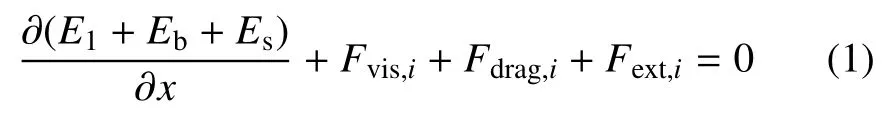
上式中,第一项是保守力,由能量函数(Ev)对位置坐标(X)求偏导获得

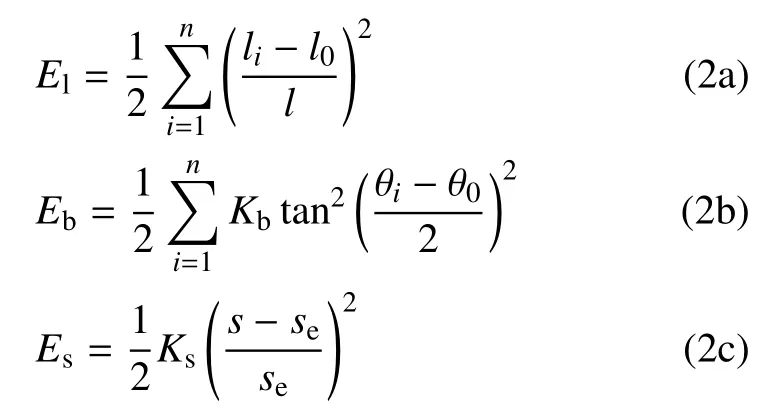
式(2a)计算拉伸势能(El),li是i单元实际长度,l0是平衡长度,K1是弹簧刚度系数;式(2b)计算弯曲势能(Eb),θi是第i个弹簧角度,θ0是平衡角度,Kb是弹簧弯曲刚度;式(2c)计算面积约束势能(Es),s和se分别是细胞当前面积及平衡面积,Ks是罚系数(penalty coefficient),取Ks≫max(K1,Kb),将细胞面积变化控制在1%.第二项考察单元节点i和j受到与节点相对速度相反的黏性力,Fvis,i=−γ(vi−vj),γ 是黏性系数.第三项是细胞接触区摩擦阻力,Fdrag,i=−µvi,µ为动摩擦系数,第四项即为外力项.

1.2 E-cad/E-cad∗调控模块

E-cad (Em) 沿细胞膜扩散并借助F-actin 锚定为E-cad∗(EI),E-cad∗又可局部形成顺式二聚体.该过程可通过非线性反应−扩散方程组描述为

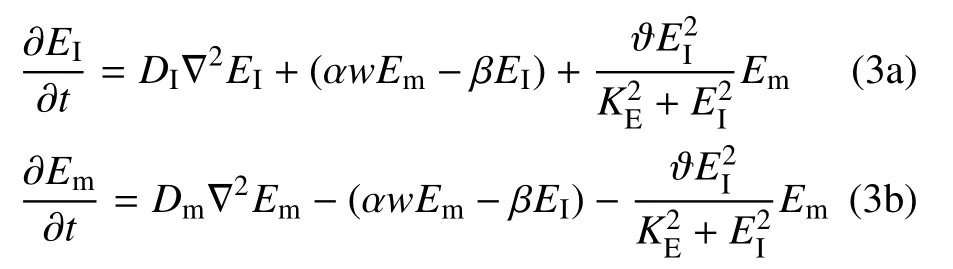
式(3a)中,右侧第一项是扩散项,DI是E-cad∗在细胞膜上扩散系数;第二项体现F-actin 介导E-cad、E-cad∗相互转化源项,w是F-actin 密度,α 及β 分别为E-cad与F-actin 结合及E-cad∗还原成E-cad 速率; 第三项体现E-cad∗通过形成顺式二聚体对自身密度反馈,ϑ是反馈速率,KE是饱和系数.式(3b)中,Dm是E-cad扩散系数(Dm>DI),后两项与式(3a)符号相反是基于E-cad∗与E-cad 总质量守恒.E-cad∗在胞间成键可采用受体-配体结合方程予以描述.

式中,R和L分别代表受体、配体,RL为受配体复合物.

依据马达−离合器机制[15],单个马达分子与Factin 结合可施加的力为Fm,驱动F-actin 以速率vm回缩,同时引起E-cad∗成键受拉.t0时刻,假设节点j上有nc,j个E-cad∗成键、nm,j个与F-actin 结合的myosin-II,该节点所受力FC,j满足

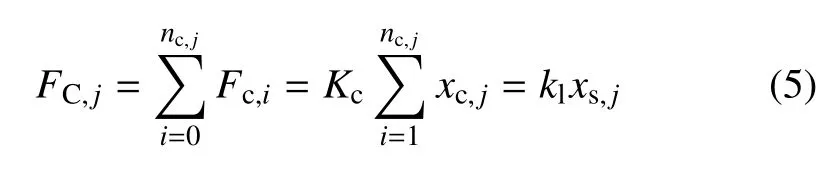
式中,Fc,i是第i个键上的拉伸力,等于该键净拉伸量(xi)与键刚度(Kc)乘积;FC,j与此处皮层张力平衡,可由节点位移xs,j、皮层刚度K1计算.t0+1 时刻,根据Bell 模型更新第i个键的解离系数

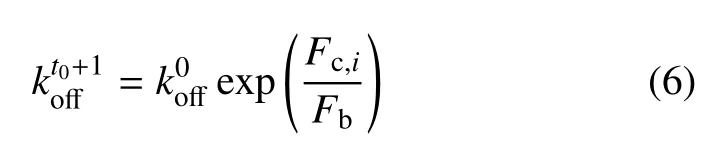
式中,Fb是特征断裂力,是0 载荷时的解离系数.随后依据力−速度(force-velocity)关系[15]更新回缩速率

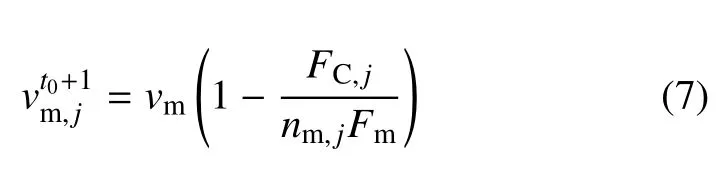
1.3 F-actin 聚合/解聚模块

单根F-actin 在刺端(pointed end)解聚为单体Gactin,用以供给钩端(barbed end) 聚合,从而以“踏车”(treadmilling)的方式更新[16-17].细胞接触区域Rac信号增强,通过激活Arp2/3 产生新的钩端,使得接触区F-actin 聚合速率加快,由此将单根F-actin 的“踏车” 行为扩展至全局.简便起见,将活性态Rac 信号(˜R)考虑为以接触中心(Ct)起始,呈指数衰减函数,即

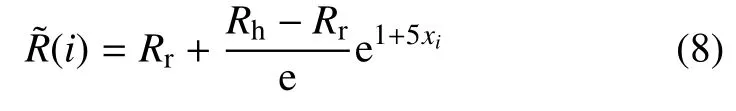
式中,Rh,Rr分别为细胞前端、后部Rac 活性系数,xi为i节点到细胞前部水平距离.

F-actin(w)、钩端(B)密度随时空调控可描述为

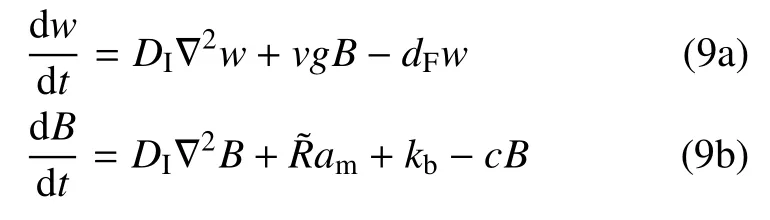
式(9a)中,右侧第一项表征F-actin 在细胞膜上缓慢扩散,第二项为F-actin 聚合反应项,v是单个钩端聚合G-actin (密度为g) 速率; 第三项是受张力调控Factin 解聚,取dF=dmax−dτ,dmax为最大解聚速率.Fτ≈0 时,dF≈dmax;Fτ≫Fhalf时,dF≈dmax−dτ.式(9b)中,am是细胞膜上Arp2/3 密度,即表征由Rac 调控钩端生成.am与胞质游离态Arp2/3 (ac) 相互转化过程由式(4) 描述,即:am,B,ac分别对应于RL,R,L.后两项中,kb,c分别是钩端生成及移除的基准速率.

2 数值方法

整体数学模型由平衡微分方程及反应−扩散方程组构成,属于力学−化学耦合问题,可采取LBP 法求解[18].LBP 是将LBM 与粒子(particle)法耦合,其中LBM 程序计算的基本内容是令“迁移”和“碰撞”两个步骤交替循环进行.

(1)碰撞

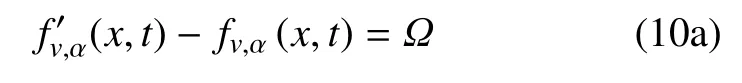
(2)迁移

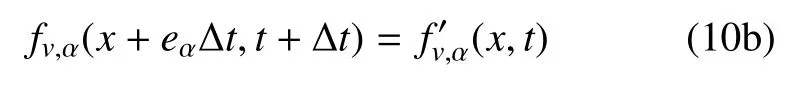
式(10)中,fv,α(x,t)是定义在离散速度方向集{eα}上的瞬时粒子分布函数;D1Q3 单元的eα取为

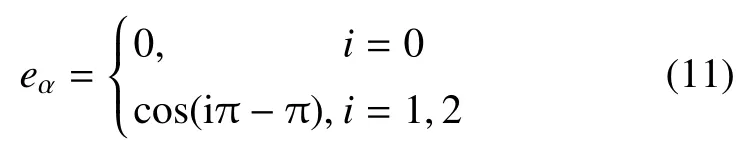
Ω 是碰撞算符,由反应项(ΩR) 及非反应项(ΩNR) 构成,即:Ω=ΩR+ΩNR.ΩNR采用单松弛模型

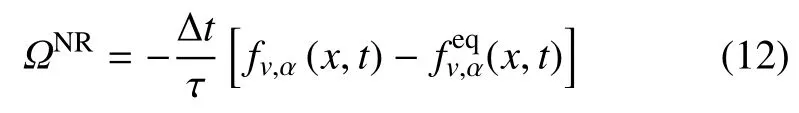
(x,t)是平衡函数

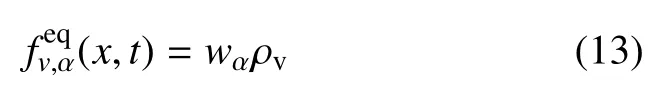
式中,ρv是宏观密度,wα是粒子速度权系数.

LBM 具有格式简单、便于并行计算、处理几何边界灵活等优点,适合求解固定边界下的反应−扩散方程组[19-20],前期工作是在计算反应源项时调用Monte-Carlo (MC) 法,从而保留系统噪音[21].LBPD1Q3 将D1Q3 单元与力学单元动态匹配,即由欧拉法获取粒子位移以更新单元长度,之后对fv,α({xi+eα∆t},t+∆t) 在网格节点{xi} 上进行3 次样条插值,由此获得fv,α({xi},t+∆t).为保证插值前、后总量守恒,设定分布函数为

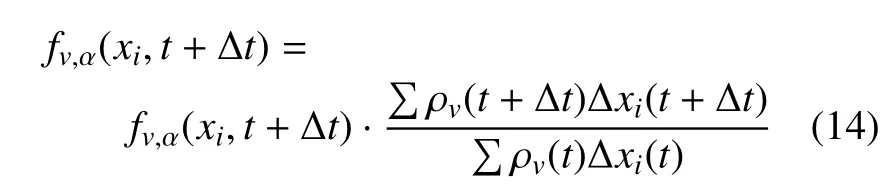
3 结果

3.1 AJs 形成动力学

考察两悬浮态细胞接触后E-cad∗,F-actin 在接触区域募集的时空动力学,以此表征AJs 形成.此前Bangasser 等针对马达−离合器机制开展参数分析[22],本文据此将“马达” 参数设定为:Fm=2 pN,vm=120 nm/s,“离合器” 参数为:k−=0.1 s−1,k+=0.3 s−1.钩端、E-cad∗及Arp2/3 初始值设定为:B=50 µm−1[17],EI=32 µm−1[17],[Arp2/3]=0.05µM[23].细胞力学及F-actin 聚合/解聚模块参数见表1.

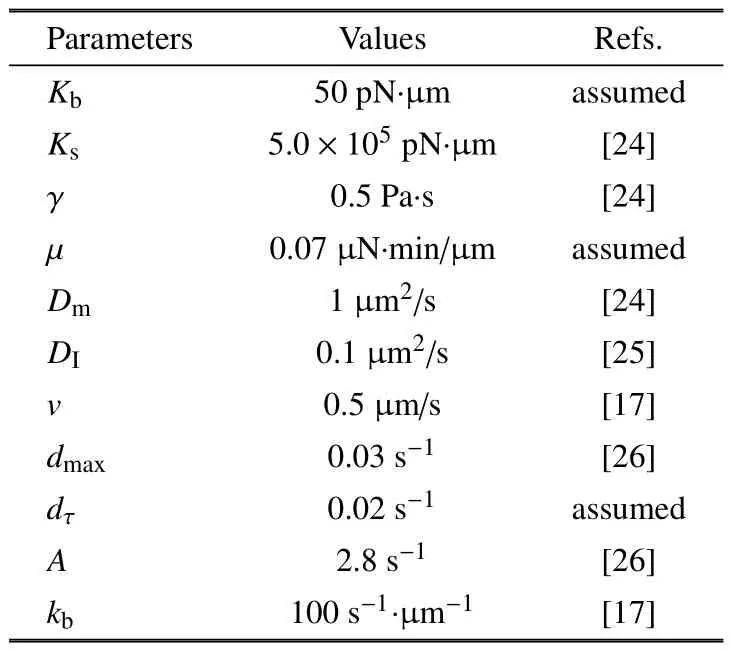
表1 模型参数Table 1 Model parameters

图2(a) 是t=20 (上)、50 s (下) 时细胞形态及E-cad∗分布图.两细胞在t=0 s 接触,此时E-cad∗均匀分布; 至t=20 s,两细胞因受到外力(Fext,i) 发生显著挤压,接触区域Rac 梯度信号令Arp2/3 局部激活进而产生少量钩端,F-actin 聚合速率提升即将少量E-cad∗锚定于此; 至t=50 s,细胞已到达平衡位置,观察到E-cad∗积聚在接触区域,而Ct 点E-cad∗密度由初始约0.3µM 提升至约0.8µM.由于扩散速率低(DI=0.1µm2/s),E-cad∗在接触/非接触交界区呈现陡峭梯度.

图2(b) 是E-cad∗时空调控图,[−π/3,π/3] 是平衡时细胞接触区域.观察到50 s 后E-cad∗依然持续募集至该区域,直至约6 min 达到稳态.E-cad∗募集与两细胞接触后产生的动态张力信号密切相关,即由myosin-II 持续地驱动F-actin 负向尾流(retrograde flow)引起胞间E-cad∗成键受拉、传导皮层张力.张力随着E-cad∗成键数增多而增强,继续通过减慢Factin 解聚锚定E-cad∗,直至E-cad∗与E-cad 相互转化速率动态平衡.

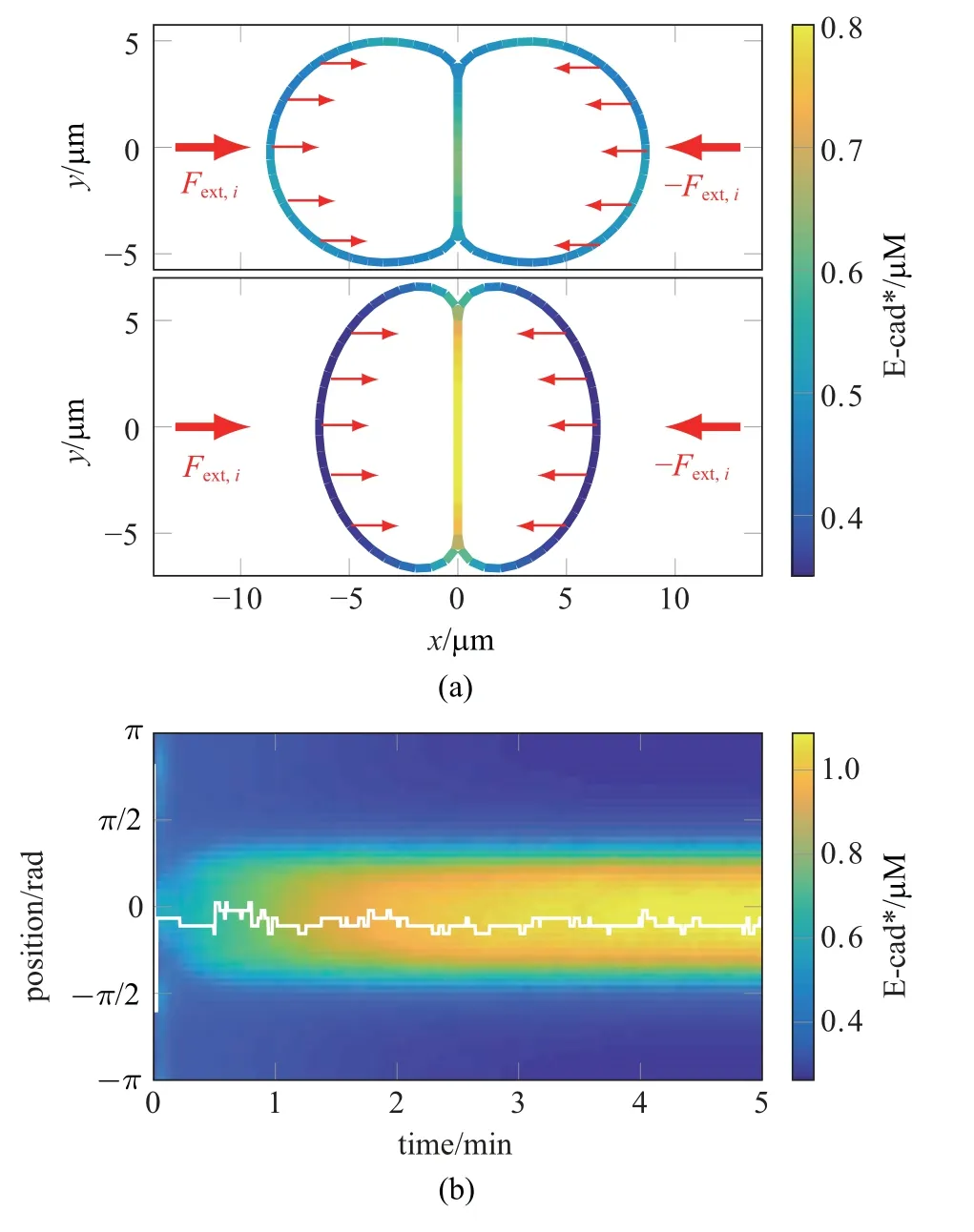
图2 (a)t=20、50 s 时细胞形变及E-cad*分布.Fext,i 是沿水平方向施加的节点外力.(b)E-cad*时空调控图.纵坐标0 点是细胞相互接触中心位置Fig.2 (a)Snapshots of cell shape and the distribution patterns of E-cad*at t=20 and 50 s. Fext,iis the external nodal force exerted alone horizontal direction.(b)Spatiotemporal regulation of E-cad*.Point 0 indicates the position of contact center

图3(a) 是Ct点处F-actin 密度时程曲线图.观察到正常情况下(ctrl 组),活性态Rac 梯度促进Factin 聚合同时张力抑制F-actin 解聚,由此产生互补效果即将F-actin 密度提高至约16 µM,接近初始时2 倍.在force−对照组中,令dτ=0 s−1以消除张力对F-actin 调控,观察到由Rac 梯度单独作用仅使得F-actin 积聚密度为约12µM;在cis−对照组中,令ϑ=0 s−1以取消E-cad∗的成束效应,此时F-actin 借助少量E-cad∗介导的张力信号将自身稳态密度恢复到约14µM.

图3(b)是相应的E-cad∗密度时程曲线图.观察到,ctrl 组中E-cad∗在F-actin 锚定及自身成束的双重反馈下产生积聚,其密度增长曲线呈现起始(0∼30 s)、快速增长(0.5∼5 min)及缓慢增长(5∼8 min)三阶段.

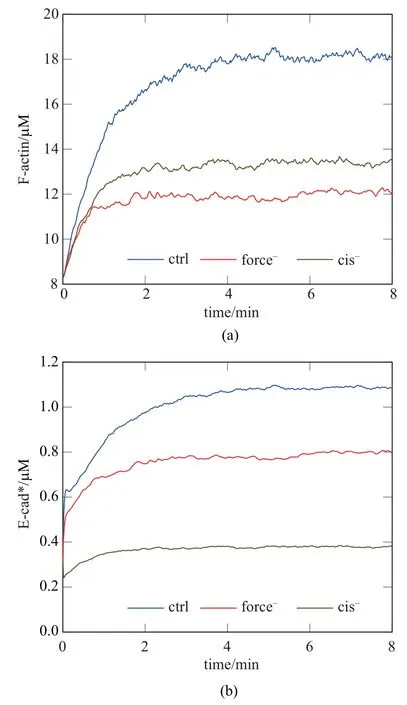
图3 Ct 点处F-actin(a)和E-cad*(b)时程曲线图Fig.3 Temporal evolutions of F-actin(a)and E-cad*(b)at Ct point

3.2 细胞皮层力学属性调控粘着连接形成

此前,尽管Murrell 等[11]观测到皮层呈现松散的非肌节元(nonsarcomeric) 结构可大幅提高马达分子收缩应变,但并未阐述皮层力学属性将如何调控AJs 建成.本节即着眼于力学反馈回路启动机制,继续探究这一问题.

首先取消Rac 梯度(即设定Rh=Rr=0.1),考察单独由张力各向异性是否可引起E-cad∗局部积聚.图4(a)是取K1=1,10 pN/nm 时获得的Ct点处Fτ时程曲线图.K1=10 pN/nm 时表征皮层呈紧密结构,观察到起始阶段(0∼100 s),皮层张力(Fτ)峰值始终较低(约75 pN).这是由于K1过大导致E-cad∗键力(Fc,i)快速增长,键的最概然寿命仅为约1 s(图4(b)),同时由于键的反复形成与断裂造成Fτ波动.Kc=1 pN/nm时可指皮层呈松散结构.较小的K1使Fc,i增长较慢,键的最概然寿命延长为约3 s(图4(b)),观察到Fτ峰值为约100 pN.由马达分子持续收缩引起E-cad∗成键受拉使得Fc,i逐渐增大,直至断裂后由其它键分担,造成键的连锁断裂,观察到Fτ呈现出周期性“加载−失效”(load-and-fail)现象[15].随着模拟持续,400∼500 s 阶段“K1=10 pN/nm”与初期相比未发生显著变化,“K1=1 pN/nm”则呈现阶梯式上升,Fτ峰值约为150 pN.由此可见,皮层为松散结构更加有利于提升皮层张力,并由此启动力学反馈回路驱动Ecad∗积聚,最终形成AJs.在force−组中,F-actin 密度最低,因此对E-cad∗锚定量最少,E-cad∗依靠成束将F-actin 赋予的初始极性放大,最终达到约0.6 µM; 在cis−组中,E-cad∗仅依赖与F-actin 锚定产生积聚,稳态时仅为约0.3µM.

综上所述并参考迄今少有争议的真核细胞极化理论[27-30],针对悬浮态细胞粘附的动力学过程亦可分为“方向感知”与“极化”.细胞接触初期,接触区域Rac 活性及皮层张力的提升为E-cad∗募集指明方向.两类信号的起效方式不同:Rac 信号受制于Arp2/3 总量,它从起效到饱和的周期短,而张力信号受制于Ecad∗密度,初始较弱但借助力学反馈回路持续增强.E-cad∗初始极性分布改变了顺式二聚体成束的局部速率,后者即为“极化”机制,可引起E-cad 向E-cad∗加速转化,直至E-cad 大量消耗而达到稳态.为定量化两类信号对AJs 的调控作用,后续将改变模型初始条件(Rac 活性或皮层张力)考察最终E-cad∗信号输出.

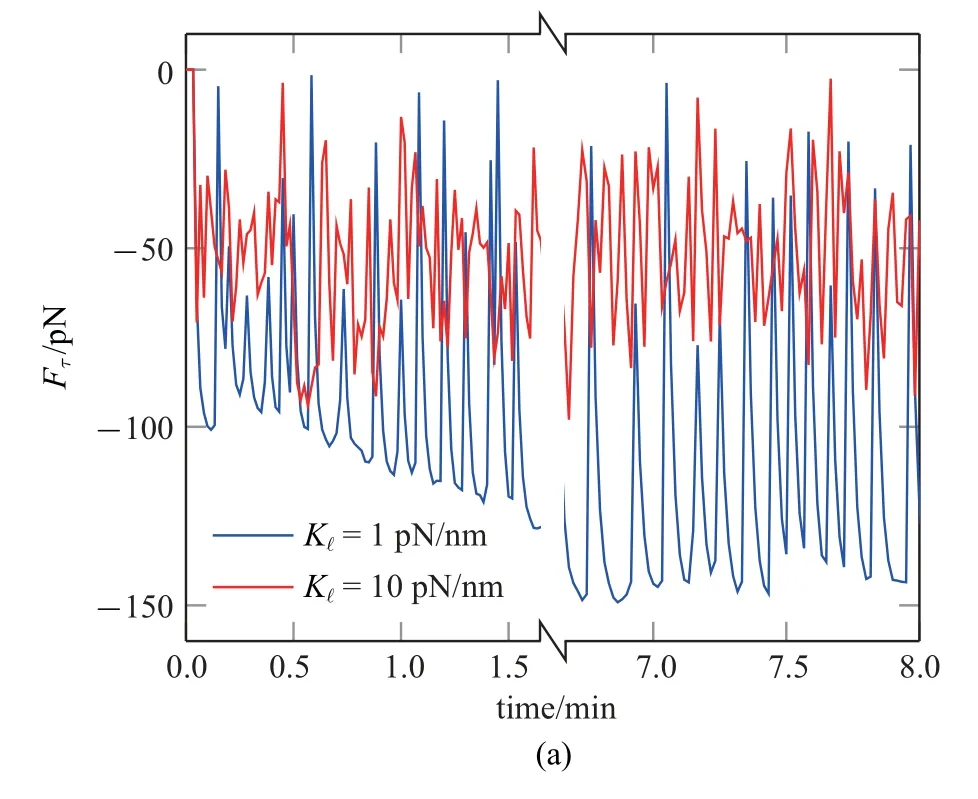
图4 (a)Kl 取1,10 pN/nm 时的Ct 点张力时程曲线图.(b)E-cad*成键最概然寿命直方图.(c)单独张力调控下E-cad*时空调控图Fig.4 (a)Time courses of the tension at Point Ct at Kl=1 and 10 pN/nm.(b)Distribution patterns of the lifetimes of E-cad∗bonds.(c)Spatiotemporal regulation of E-cad∗in the presence of the tension alone

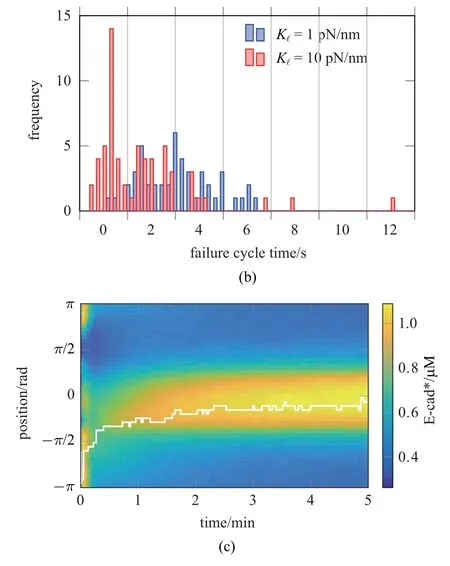
图4 (a)Kl 取1,10 pN/nm 时的Ct 点张力时程曲线图.(b)E-cad*成键最概然寿命直方图.(c)单独张力调控下E-cad*时空调控图(续)Fig.4 (a)Time courses of the tension at Point Ct at Kl=1 and 10 pN/nm.(b)Distribution patterns of the lifetimes of E-cad∗bonds.(c)Spatiotemporal regulation of E-cad∗in the presence of the tension alone(continued)

图4(c) 是K1=1 pN/nm 时E-cad∗时空调控图.与图2(b)对比,由于缺少活性态Rac 梯度,E-cad∗的初始积聚位置并不位于接触中心.这是由于该阶段张力各向异性程度较低,不具有明确的E-cad∗积聚信号,E-cad∗通过自身成束效应制造了随机高点.随着模拟时间推进,力学反馈回路逐渐开启,E-cad∗积聚方位逐渐向接触中心偏移(图中白色线).

3.3 细胞接触长度调控AJs 形成

实验中通过调节双微吸管间距来控制细胞挤压程度[14],模拟时施加不同挤压力(Fext,i)即可达到相同效果.图5(a)即考察缺少Rac 梯度时,细接触区弧度由2π/9 扩大至8π/9 时获得的稳态E-cad∗分布.随着接触区扩大,细胞后部的E-cad∗密度降低.弧度为2π/5 时,E-cad∗峰值最高(达到约0.90µM),说明中等长度的接触区促进AJs 成熟.接触区过小时输入的张力信号较弱,从而限制整体力学反馈回路强度;接触区过大时高密度E-cad∗分配范围过大导致峰值降低,同样会限制AJs 成熟.图5(b) 是加入Rac 梯度信号(Rh=0.3)后的E-cad∗分布.与图5(a)对比,细胞前、后部密度与接触区弧度关系依然存在,但分布更为陡峭.图5(b)插入图是令接触区在[0,2.7]弧度变化时获得的Ct点处E-cad*峰值浓度曲线图.观察到该曲线呈现双相性,E-cad*最高峰值浓度发生在1.2 接触弧度附近.

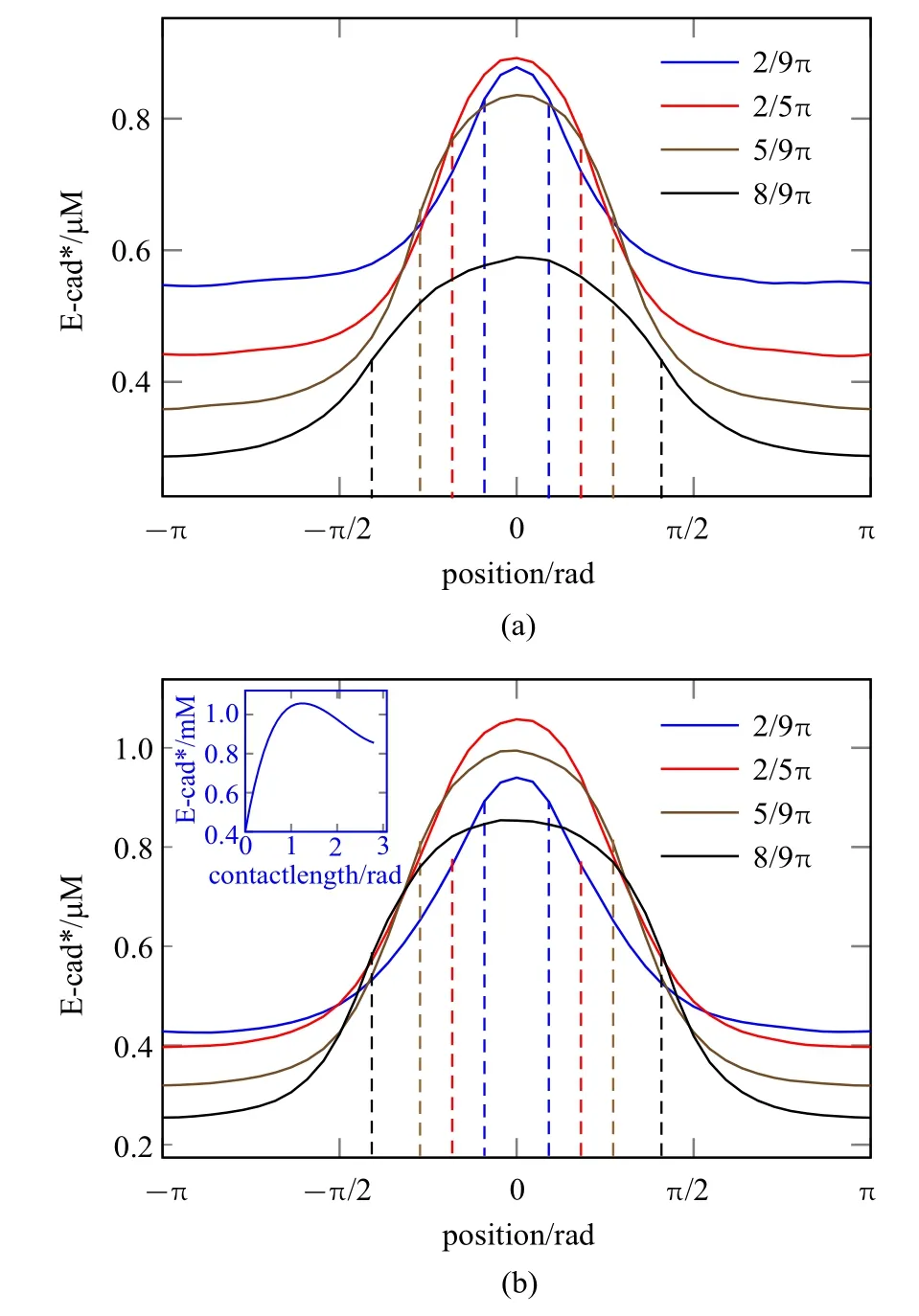
图5 Rh=0.1(a)或0.3(b)时不同接触长度下的E-cad*稳态分布图.(b)中的插图显示E-cad*峰值浓度随接触区长度呈双相性变化Fig.5 Profiles of E-cad*at Rh=0.1(a)and 0.3(b)upon different extrusion deformations.Inserted panel in(b)shows the dependence of maximum E-cad*concentration with the contact length

图6 是将Rh和K1进行参数组合获得的E-cad∗稳态分布.取K1=1,5,10 pN/nm,同时取Rh=0.1,0.3,0.5,由此获得9 组(K1,Rh).由于Fext,i为常量,细胞挤压程度由K1控制,K1越大则挤压程度越低.观察到(1,0.5)组合下E-cad∗呈现显著积聚,这是由于Rac 梯度信号最强,而K1低可引起接触区扩大、Ecad∗成键寿命延长;相反取(10,0.1)时,力学、化学信号均最弱,使得E-cad∗积聚程度最低.取(1,0.1)、(10,0.5) 时,E-cad∗积聚程度接近,说明当张力信号较弱时可由增强局部Rac 信号予以补偿,反之亦然.

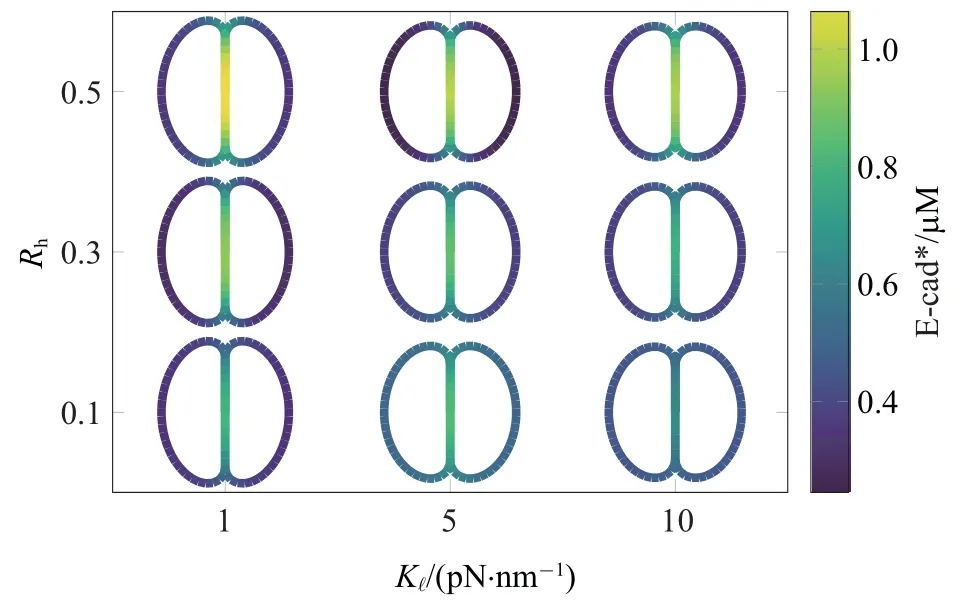
图6 Kl 与Rh 进行参数组合所获得的E-cad*稳态分布图Fig.6 Stable distribution patterns of E-cad*derived from different combinations of Kland Rh

4 讨论

生物化学学者开展悬浮态细胞粘附实验往往配合分子抑制/过表达对照组实验.分子间级联转导如何调控分子在细胞局部积聚动力学?对于这一细胞−分子“跨尺度”问题需要借助构建力学−化学耦合模型予以回答.此前Chu 等[14]采用转染E-cad 的悬浮态S180 细胞开展粘附实验,通过控制两细胞接触时间并测算分离力(与E-cad∗积聚程度正相关)将AJs的建立过程划分为:起始、快速增长及缓慢增长阶段.本文数值模拟获得E-cad∗调控空间分布特征及演化趋势与该实验一致,但达到稳态所需时间较Chu 实验快(约5 min vs.约30 min),原因之一是忽略了G-actin自身调控,即G-actin 主要以ADP 结合态存在,需要与捕获蛋白ADF/cofilin,profilin,Thymosin 发生交换成为ATP 结合态方能供给钩端聚合[17].Chu 等[14]所开展的对照组实验包括有:(1)采用Latrunculin 抑制F-actin 聚合后,观测到AJs 无法形成;(2)表达Rac 显性失活突变体后,AJs 成熟度降低了35%.参照本文图6 可对上述观测结果作如下解读:尽管F-actin,Rac都参与E-cad 力学反馈回路,但Rac 位于F-actin 上游,其促进F-actin 聚合的作用可由张力降低F-actin 解聚予以补偿,因而Rac 失活只会削弱但并不阻止AJs建成.

本文为构建整体数学模型采取了必要的假设及简化,今后可继续开展以下工作.

首先,模型假设Rac 活性系数由细胞接触区以指数形式衰减,未引入Rac 自身调控机制.此前Mori 等针对Rac (或Cdc42) 调控提出了波桩(wave-pinning)模型[31],即考察Rac 失活/活性态转化,活性态Rac扩散较慢并正向调控自身生成,由此造成了其在一侧激活即以波的形式向对侧传播,最终受到失活/活性态总体质量守恒限制达到稳定的极性分布.已证实E-cad 与整合素(integrin)通过Rho GTPase 发生交互式调控[32-33],继续引入Rho GTPase 调控模块可将悬浮态细胞粘附模型拓展至贴壁细胞[34].

其次,模型对E-cad,F-actin 力学传导结构是采取“最弱结合点”假设[15],将胞间E-cad∗成键作为一系列“串联弹簧”的失效点,将其考虑为滑移键(slip bond).此前原子力显微镜、光镊等单分子实验证实了cadherin-catenin 复合体与F-actin 或是胞间E-cad∗成键均存在逆锁键(catch bond)[35-36].基于本文力学−化学耦合体系,后续可从力学反馈回路的启动机制出发,探讨逆锁键对AJs 的调控作用.

最后,本文通过LBP 法求解包含级联信号转导的细胞力学问题,未考察细胞与环境流体间相互作用.此前Dallon 等[25]基于浸入式边界法(immersed boundary method,IBM) 构建了悬浮态细胞粘附的流体−固体耦合模型; Tanaka 等[37]将IBM 与LBM 结合并应用于组织形态发生(morphogen)领域.受此启发,今后可发展IB-LBP 法.

5 结论

本文考察胞间E-cad∗成键介导actomyosin 皮层上的Rac 活性及张力信号反作用于E-cad 级联转导,由此构建了悬浮态上皮细胞粘附的力学−化学耦合模型,并通过自行发展的LBP-D1Q3 法予以数值求解.正常组数值模拟首先重现了细胞粘附实验中观测到E-cad∗和F-actin 在细胞接触区持续募集的现象,继而结合对照组获得了以下3 方面主要结论.

(1)局部活性态Rac、张力信号分别调控F-actin聚合、解聚,由此发挥互补效应造成F-actin 在细胞接触区域富集,通过锚定作用帮助E-cad∗建立初始极性; E-cad∗通过形成顺式二聚体将初始极性放大,由此E-cad∗时程曲线呈现起始、快速增长及缓慢增长阶段.

(2) 单独张力各向异性经 “E-cad →张力→Factin” 力学反馈回路放大即可造成E-cad∗积聚; 在马达分子拉动下,E-cad∗成键寿命与皮层刚度相关,而松散的皮层结构具有较小刚度,E-cad∗成键寿命延长、张力提升,有利于力学反馈回路的启动.

(3)细胞接触区长度适中时,整体张力输入信号经力学反馈回路放大使得E-cad∗局部积聚最为显著,因此接触区长度可作为控制粘着连接成熟度的有效手段.