基于巴西盘试验的海冰拉伸强度研究1)

陈晓东 崔海鑫 王安良 季顺迎,2)

∗(大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116024)

†(中国船舶及海洋工程设计研究院,上海 200011)

∗∗(国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室,北京 100081)

引言

对于寒区的船舶与海洋结构,冰载荷是主要设计参数[1].海冰在与斜体结构相互作用时,以弯曲破坏为主.海冰的拉伸强度决定了海冰的破碎尺寸以及结构冰力周期等特征[2-3].对于直立结构与海冰的相互作用,海冰可表现出弯曲与劈裂等多种破坏模式.海冰的拉伸强度是决定破坏模式的重要因素并因此影响了载荷形式[4-5].一般来说,单轴拉伸试验是获取材料拉伸强度的最直接手段.但由于海冰材料本身的脆性特点,在进行单轴拉伸试验中破坏处容易发生在试样夹持部位而导致试验失败.为提高试验的成功率,需将拉伸试样打磨成中间截面较小的“哑铃”状以使试样由中部发生破坏[6-8].在该过程中,试样的加工制备需要大量时间而严重影响了试验效率,因此也并不适用于现场试验环境[9].

为提高试验效率,相关学者通过对试验方法的改进来获取脆性材料的拉伸强度,主要包括三点弯曲试验、悬臂梁试验与巴西盘劈裂试验等[10-12].在海冰的压缩试验中,虽然加载端受到压缩作用,但试样中部可产生明显的拉伸变形[13-15].由于脆性材料本身的拉伸强度远远小于其压缩强度,因此可通过改变试样的几何形状使其在压缩过程中以拉伸形式发生破坏,从而得到其拉伸强度[16-17].在岩石力学中,通过对圆盘形状的试样施加对称的轴向压缩载荷,使其中心部位形成强烈的拉伸应力并最终劈裂破坏并以此计算其拉伸强度,该试验又可称为巴西盘劈裂试验[18-20].在该方法中,切割打磨试样等繁琐步骤得到了简化,与单轴拉伸试验相比测试效率得到了明显提高.同时,试验结果表明巴西盘劈裂试验可同时获得材料的拉伸与压缩弹性模量[21-22].在对冻土的力学性质研究中,该方法同样得到了合理的结果[21,23-24].Kovacs 与Kalafut 最早将该方法应用在海冰的拉伸强度测试中.由于试验中所采用的液压装置无法控制以获得准确的加载速率,海冰在加载过程中的变形改变了载荷状态并对试验结果造成了较大的影响[25-26].为解决该问题,Rocco 等[18]和Yu等[27]通过对解析解的改进得到了均布载荷作用下的拉伸强度求解方式.在实际试验中,将圆盘试样的两端切割成平面则可得到均布载荷的加载状态,从而避免冰的变形对拉伸强度计算结果的影响[28-30].采用巴西盘劈裂试验方法,将大幅度提高海冰材料拉伸强度的测试效率.目前,仍未有采用巴西盘劈裂试验对海冰拉伸强度开展相对系统的试验研究.

为此,本文以渤海辽东湾沿岸的粒状冰为试验对象,采用巴西盘劈裂试验对粒状冰的拉伸强度开展了系统的研究.通过试样破坏过程中的裂纹形式以及最大屈服力特点,分析了该方法对于获取海冰拉伸强度的可行性与有效性.此外,试验进一步研究了试样厚度、温度以及加载速率等条件对试验结果的影响.

1 巴西盘劈裂试验方法与原理

1.1 试验仪器及步骤

典型的巴西盘劈裂试验中,实际上对试样所施加的是轴向压缩力,因此本文采用万能试验机作为加载系统提供单轴压缩载荷.通过试验机加载台面的轴向移动,对试验试样形成稳定的加载速率.其中试验机的系统刚度约为海冰试样的50 倍以上,因此在加载过程中由于系统刚度所引起的变形误差可忽略不计.

在试验过程中,首先对海冰进行采样并加工成为圆盘形状; 其次,将圆盘放置于加载台(如图1 所示) 并通过横梁的匀速运动施加载荷; 最后,在圆盘试样达到失效强度并发生破坏后停止试验.加载过程中,通过力传感器与位移传感器以200 Hz 的采样频率记录加载力与横梁位移.在每组试验完成后及时测量每个试样的温度;同时,将试样的一部分封存融化,采用电导计对盐度进行测量;试样另一部分采用浮力法对其密度进行测量[31].

图1 巴西盘劈裂试验装置Fig.1 Experimental setup of the Brazilian tests

试验采用了0.04 mm/s 与0.1 mm/s 两种加载速率与−4.5◦C,−10◦C,−18◦C,−30◦C 四种温度以及三种不同的试样厚度.加载台表面采用较为光滑的不锈钢材料,但在加载过程中并未有试样发生滑动偏移,这说明摩擦力对加载过程的影响并不显著.

1.2 海冰试样及其物理性质

本文所采用的海冰试样采集于渤海辽东湾鲅鱼圈海域.采集试样过程中所测量的海水盐度为33.4‰∼33.6‰.该海域的潮汐为典型的半日潮,海冰在潮汐作用下发生漂移并相互挤压重叠,如图2(a)、图2(b)所示.图中能够清晰看出海冰相互挤压后形成的“指状”尼罗冰.在采样过程中可观测到浮冰下部堆积着大量的絮状碎冰,是在浮冰相互剪切过程中所形成.当海冰运动停止后,絮状碎冰再次冻结则形成颗粒结构的海冰,如图2(c)所示.试样所采用的圆盘直径为110±3 mm,对圆盘试样冰晶进行观测则如图2(d)所示.

图2 海冰试样采集及其细观结构Fig.2 Collection and texture of the ice sample

图2 海冰试样采集及其细观结构(续)Fig.2 Collection and texture of the ice sample(continued)

本次试验共计完成40 组,其中海冰的盐度与密度分别为6.7±3.1‰与849±52 kg/m3.根据试验过程所记录的试样盐度、温度与密度数据,采用Cole 与Weeks 的方法进一步对海冰的孔隙率与卤水体积进行了计算,结果列于表1 中[32].其中卤水体积主要分布在10‰∼30‰,而总体孔隙率分布则较为分散.卤水体积与孔隙率分布特征的差异也说明了试样中空气含量分布相对离散.

表1 粒状冰试样中的卤水体积及孔隙率分布[32]Table 1 The distribution of brine volume and total porosity of granular sea ice[32]

1.3 海冰试样的应力状态及拉伸强度计算方法

巴西盘劈裂试验的主要优势是通过施加平行于圆盘截面的压力来测量并计算其拉伸强度.因此试样内部的应力状态以及拉伸强度的计算则成为试验的主要理论基础.由于圆盘的厚度远小于直径,若考虑加载过程中加载面与圆盘之间的接触状态,则可将圆盘的应力状态简化为准二维问题.此时,接触部位的线载荷则可视为点载荷P,如图3 所示.

图3 对称点载荷作用下圆盘内部的应力分布Fig.3 Stress distribution within a disc under symmetrical point load

对于各向同性材料在对称集中载荷作用下的应力分布状态已由Muskhelishvili(1955)给出.圆盘内坐标点(x,y)的应力状态极坐标表达式为[22]

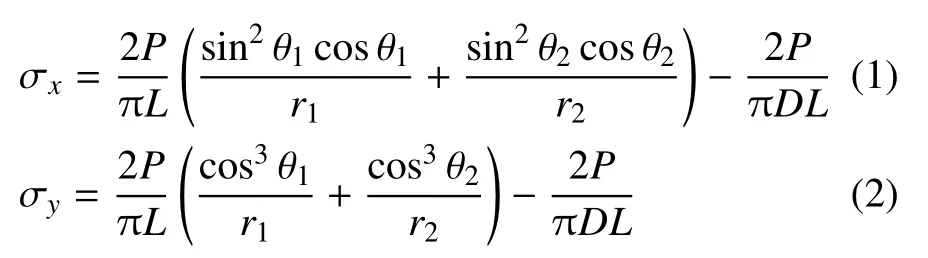
式中,σx与σy分别为所选点S在x与y方向上的正应力;r1与r2为该点到载荷施加处A与B的距离;θ1与θ2为连接线与y方向的夹角;P为点载荷;D为圆盘直径;L为圆盘厚度.

当所选点S位于y轴即x=0 时,则式(1) 与式(2)写为

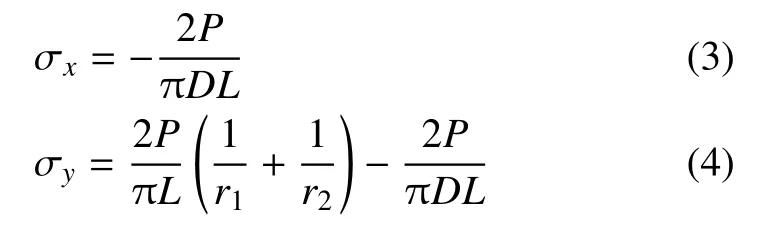
基于式(3),通常认为试样发生破坏时所达到的拉伸强度为

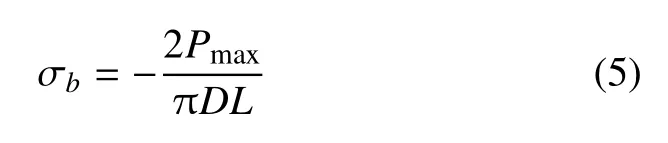
式中,Pmax为最大加载力;σb为拉伸强度.

由式(1)∼式(5)可得到对称点载荷下,材料破坏时的拉伸强度.然而,海冰在加载过程中的变形影响了加载状态.此时仍采用基于点载荷的理论解则会产生明显的误差.为此,Rocco 等[18]在考虑变形后,引入了修正系数β 对式(5)进行了改进

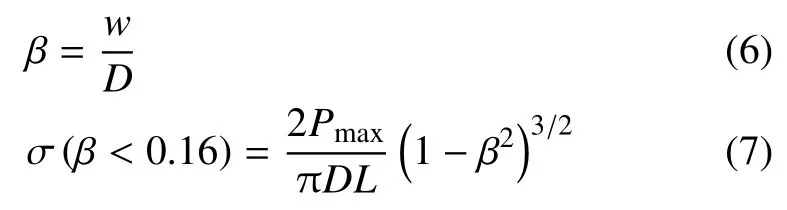
式中,w为圆盘变形后加载处的宽度,如图4 所示.

图4 加载面与试样接触处的形变量Fig.4 The deformation of ice-platen contact area

若假设试样在加载过程中的变形集中在试样与加载面接触处,则可认为试样变形与加载面的位移相关.对于加载速率恒定时,则w为

式中,rf为破坏发生时试样中心到加载面的距离.

2 巴西盘劈裂试验结果与分析

为研究巴西盘劈裂试验获取海冰拉伸强度的有效性,试验过程中对圆盘的最终破坏形式进行了记录.同时,研究了圆盘厚度、试样温度、加载速率等因素对试验结果的影响.

2.1 巴西盘破坏形式

在每组试验完成后,试样的最终破坏形式如图5所示.虽然试验中改变了试样的厚度、温度与加载速率等条件,但总体上试样的破坏模式较为统一.由于试验过程中的裂纹发展速度较快,并未观察到裂纹的产生位置及扩展过程.但综合试样最终的裂纹形状与理论模型中圆盘试样内部的应力分布特征,可推断试样在中心位置达到拉伸强度后发生破坏.该理论公式已广泛应用于混凝土与岩石等材料的拉伸强度测试中,因此也适用于海冰这种脆性材料.部分裂纹并未完全沿轴线发展,如图5 中的No.4 和No.20等几个试样.这主要由于海冰内部的空气或卤水体积等初始缺陷在裂纹发展过程中改变了其路径.在No.25 试样中能够观察到试样左侧具有明显的卤水通道,但该缺陷并未影响裂纹的发展路径.

图5 巴西盘劈裂试验试样的最终破坏形式Fig.5 The failure mode of sample from the Brazilian tests

根据式(1)与式(2)中的应力状态可知,在加载过程中圆盘y轴轴线上产生最大拉伸应力并沿水平方向逐渐降低.在高应力区域即靠近试样中轴线部位,卤水体积或气泡等原始缺陷会对裂纹发展路径产生一定的影响.在远离中轴线高应力区的位置,即使有明显的初始缺陷也并不会对裂纹发展路径产生影响.

从破坏模式来看,试样均在达到拉伸强度后发生破坏.这说明通过巴西盘劈裂试验能够有效测量海冰的拉伸强度.但由于海冰内部的天然缺陷,在试验过程中会对裂纹路径产生一定的影响并使试验数据产生较大的离散性.在后面将结合实测数据进一步对分析这种离散特征.

2.2 试样厚度对试验结果的影响

在拉伸强度的理论计算中,为简化求解过程而采用了准二维理论模型.但在实际上圆盘试样是具有一定厚度的三维结构,厚度的增大将带来实验结果的误差.为此,本文分别采用了3 种不同试样厚度,并分析厚度与直径比(L/D)对试验结果的影响.

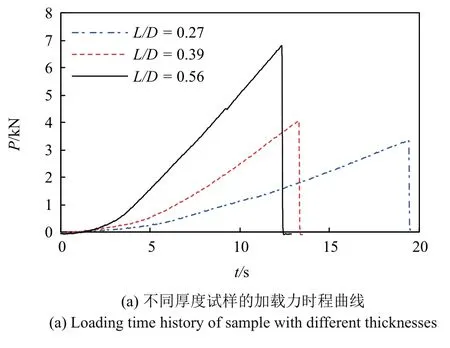
图6 试样厚度对试验结果的影响Fig.6 The influence of sample thickness on the result

图6(a) 给出了不同L/D下的加载力时程曲线.从图中能够看出,随着试样厚度即L/D的增大破坏时的最大载荷明显提高.同时,时程曲线的斜率却随着厚度的增大逐渐升高.在1.3 节所推导的理论解中,将试样的应力状态假设为二维问题,在计算过程中需要进一步得到加载力的线载荷.图6(b)给出了不同L/D下的线载荷时程曲线.从图中能够看出,L/D对线载荷的最大值影响并不显著.这说明,在本文试验中所采用的3 种不同L/D下,圆盘厚度所引起的拉伸强度计算误差相对较小.但值得注意的是,虽然L/D对最大加载力的影响较小,但却改变加载力/线载荷时程曲线的斜率.巴西盘试验中试样主要承受压缩作用,斜率的改变说明试样厚度实际上影响了圆盘的名义弹性模量.

2.3 加载速率对试验结果的影响

图7(a)给出了不同加载速率下的加载力时程曲线.从时程曲线中能够看出,在两种加载速率下的最大加载力变化并不显著.但在高加载速率下,加载力的上升速度较快.若进一步考虑试样在y轴方向的变形量即横梁的位移,则加载力与横梁在y轴上位移关系如图7(b)所示.从图7(b)中来看,两组曲线的总体趋势基本一致,在破坏前的最大加载力略有不同,这主要是由海冰本身内部缺陷的离散性所导致.

图7 加载速率对试验结果的影响Fig.7 The influence of loading speed on the results

图7 加载速率对试验结果的影响(续)Fig.7 The influence of loading speed on the results(continued)

2.4 试样温度对试验结果的影响

海冰内部的卤水体积随着海冰温度不断发生变化并对海冰拉伸强度等力学性质产生影响.本文所采用的海冰试样通过现场采集所得,试样生长过程中的温度环境一致.在海冰生成后,环境温度的改变仍会对其力学性质产生影响,因此在试验中采用4 种不同的环境温度对海冰试样开展了巴西盘试验.

图8(a)给出了不同温度下的加载力时程曲线.从试验结果能够看出,加载力峰值随着温度的降低逐渐升高.随着温度降低,海冰内部的卤水逐渐冻结为固态冰晶,从而提高了拉伸强度.同时,温度的升高也改变了试样的名义弹性模量,增大了试验过程中的变形量.这也说明,海冰在加载过程中存在着明显的变形,并影响了拉伸强度的计算.

采用式(7)对拉伸强度进行计算,则得到拉伸强度随温度的变化趋势,如图8(b)所示.图中分别给出了两种加载速率下拉伸强度随温度变化的试验结果,并对两组试验结果进行了曲线拟合.总体来看,拉伸强度与试样温度间呈线性递减关系.在改变加载速率以后,试验结果的变化趋势以及拟合曲线相一致,这也说明了本文所采用的两种加载速率对拉伸强度试验结果影响较小.此外,数据点的分布表现出明显的离散性,这与2.1 节破坏模式中所分析的机理相一致.

图8 试样温度对试验结果的影响Fig.8 The influence of sample temperature on the results

2.5 试样孔隙率对试验结果的影响

海冰的拉伸强度受温度、盐度与密度等多种因素共同影响,但最直接的影响因素应为海冰孔隙率.孔隙率表示海冰内部的液态盐水与空气所占比例,同时也反映出海冰内部固态冰晶的比例.在海冰拉伸破坏过程中,主要由固态冰晶来承载拉伸应力,因此,孔隙率是决定海冰拉伸强度的直接因素.

根据1.2 节所测得的数据,得到了拉伸强度随孔隙率的变化,如图9 所示.为分析巴西盘劈裂试验在获取海冰拉伸强度的有效性,将本文测试结果与单轴拉伸试验结果进行了对比.由于目前国内外尚未有对粒状海冰拉伸强度开展过相关研究,因此仅给出柱状冰拉伸强度的测试结果进行对比分析.图9中分别给出了相关文献中单轴拉伸试验的测试结果以及Timco 与Weeks[1]所总结的拉伸强度−孔隙率关系的经验曲线.其中黑色实线为加载力垂直于柱状冰晶时所得到的拉伸强度,蓝色虚线表示加载力平行于冰晶方向时的拉伸强度.

图9 拉伸强度随孔隙率的变化规律[1,8,33-34]Fig.9 The relationship between tensile strength and total porosity[1,8,33-34]

总体来看,粒状冰的拉伸强度随孔隙率的增大而降低.其中拉伸强度数据点的分布表现出明显的离散性,该特点与2.1 节破坏过程分析结果相一致.由拉伸强度与孔隙率之间的变化趋势能够看出,巴西盘劈裂试验所得到的结果与单轴拉伸试验结果相一致.这说明本方法所得到的结果能够有效反映海冰拉伸强度的变化特征.

若对比本文所得到的拉伸强度与单轴拉伸试验的测试值,则本文所得到的结果明显偏高.虽然本文所采用的试样为粒状冰,但参考Timco 与Weeks[1]对单轴压缩强度特点的分析,粒状冰的强度通常介于柱状冰的水平加载方向与竖直加载方向之间.也就是说,粒状冰的拉伸强度应低于柱状冰竖直方向的拉伸强度,即图9 中的蓝色虚线.但本文所得到数据点明显高于该曲线,这说明巴西盘劈裂试验所得到拉伸强度要高于海冰的真实拉伸强度即采用单轴拉伸试验所测得的结果.这里的偏差主要来自于巴西盘劈裂试验中对拉伸强度计算过程的简化.在理论推导中,假设试样在加载过程中的变形全部产生在试样与加载面接触处,而实际过程中的变形应分布于整个试样.同时,在试样发生变形后认为点载荷转变为均布载荷.而实际加载中由于试样在水平方向上的变形,加载面处于更为复杂的应力状态.因此,为得到更为准确的拉伸强度,还需对巴西盘劈裂试验中理论计算进一步改进.

2.6 试验结果的误差分析

对于巴西盘劈裂试验,试验结果的误差一部分来自于加载系统,另一部分来自于试样的加工精度与材料的非均匀性.本文所采用的加载系统刚度比圆盘试样刚度高约两个量级,对试验结果的影响可忽略不计.由于本文所采用的圆盘试样直径远大于厚度,因此圆盘不同表面之间的垂直度将影响试样内部的应力分布并及破坏强度.同时,因为理论解是建立在试样为理想圆形的基础上,所以试样的圆度也会增大拉伸强度结果的误差.此外,海冰内部空气与卤水等成分所形成的天然缺陷在试样受力过程中更易形成应力集中现象,使试样发生破坏从而降低了所得到的强度.

2.7 试验结果的有效性分析

为分析试验结果的有效性,将采用相关试验结果与本文试验结果进行对比分析.考虑本文所采用的试样采集地点为渤海湾,应与渤海海冰相关试验测试结果进行对比.但目前尚未有系统的工作对渤海海冰的拉伸强度进行测试.鉴于海冰的弯曲试验结果与拉伸试验结果有较高的相关性,可与弯曲试验结果进行对比分析.渤海海冰的三点弯曲强度测试结果显示,海冰弯曲强度随卤水体积的增大呈减小趋势,这与本文结果的参数统一表征是相一致的[35-36].

将试验结果与渤海海冰相关试验结果及国外海冰单轴拉伸强度测试结果进行对比分析可知,在本文所采用的试验系统与计算方法下所得到结果具有很好的有效性与可靠性.在渤海海冰工程设计及数值模型的参数选取可参考本文的测试结果,即当海冰孔隙率在10‰与75‰之间时,其拉伸强度的范围为1.0 MPa 至2.8 MPa[37-38].

3 结论

为研究巴西盘劈裂试验在对海冰拉伸强度测试的有效性与准确性,本文对渤海辽东湾沿岸粒状冰开展了系统的巴西盘劈裂试验研究.试验中研究了试样厚度、加载速率以及试样温度等条件对拉伸强度测试结果的影响.同时,在拉伸强度的计算公式中考虑了圆盘在加载过程中的变形量对计算结果的影响并进行了相应的修正.结果表明:海冰在巴西盘劈裂试验中最终以拉伸形式发生破坏,由此可知该试验能够有效反映海冰的拉伸强度; 在本文所采用的试验参数范围内,试样厚度−直径比与加载速率对拉伸强度的计算影响较小; 粒状冰的单轴拉伸强度随卤水体积的增大而减小; 巴西盘劈裂试验所测得的海冰拉伸强度为1.0∼2.8 MPa.