纵向缺失数据下高维部分线性回归模型的变量选择

田瑞琴，徐登可

(1. 杭州师范大学理学院，浙江 杭州 311121； 2. 浙江农林大学理学院，浙江 杭州 311300)

0 引言

纵向数据广泛地产生于经济学、医学、生物学和社会学等领域，它是指同一个体在不同时间点上观测获得的重复观测数据.由于数据结构中的重复观测性质，容易导致其产生数据的缺失.例如，有些研究个体会在某次实验缺席或者在实验结束之前退出研究.最简单的处理缺失数据的思想是直接对完全观测数据进行分析.但是，当缺失数据的机制不是完全随机缺失时，所得的统计推断结果会出现较大的偏差.近年来对纵向缺失数据的研究发现，单调缺失和非单调缺失是两种主要的缺失模式，其中单调缺失主要是指在实验中部分研究个体因为某种原因在某一个时刻退出该实验后再也没回来继续实验，这样获得的缺失数据称为单调缺失数据，否则称之为非单调缺失数据.例如，文[1]研究老年痴呆症疾病，由于病人发展成痴呆患者而放弃了该项研究，所获得的数据即为单调缺失数据.目前针对纵向缺失数据模型的参数估计问题已有不少研究，但是大多集中在协变量维数是固定的情况下.Robins等[2]针对非单调缺失机制下纵向数据半参数模型，基于逆概率加权广义估计方程(IPW-GEE)研究分析了模型的参数估计问题.Qu等[3]基于无偏估计函数方法对具有随机缺失的相关数据模型提出了一种有效的参数估计方法.文[4-7]也对此类相关问题展开了研究.

另外，很多学者针对协变量是发散维的高维纵向数据回归模型进行了变量选择研究.例如，Xu等[8]针对协变量发散维的相关二元数据模型，提出了一种基于惩罚加权最小二乘的变量选择方法.Dziak[9]针对高维纵向数据模型提出了基于SCAD惩罚二次推断函数的变量选择方法.Yang等[10]针对高维部分线性模型提出了Dantzig变量选择方法，最后能同时获得参数部分和非参数部分的估计.Wang[11]针对协变量是发散维的高维纵向数据模型，拓展了广义估计方程分析方法的渐近理论.Tian等[12]针对高维数据下纵向部分线性回归模型，基于光滑阈广义估计方程方法研究分析了模型的变量选择.综上所述，目前针对带有缺失数据或高维数据的纵向数据回归模型的研究成果已经比较丰富，但甚少涉及缺失数据下高维纵向回归模型的变量选择问题.现有的变量选择方法大部分是基于惩罚函数(例如SCAD惩罚、Adaptive LASSO惩罚等)进行压缩估计.由于惩罚函数在0点是奇异的，所以基于惩罚估计的变量选择算法就要面临去解决一个涉及非凸函数最优化的问题.为了解决这个问题，Ueki[13]提出了一种基于光滑阈估计方程(SEE)的变量选择方法.这种方法能自动地剔除不重要的变量，同时得到重要变量的参数估计，并且此变量选择算法中不涉及凸优化的问题.Lai等[14]将这种光滑阈估计方程思想应用到纵向数据单指标模型上.Li等[15]和Tian等[16]基于光滑阈估计方程思想并结合广义估计方程分别研究分析了纵向数据下广义线性模型和纵向数据下变系数部分线性模型的变量选择.

本文针对单调缺失数据下纵向高维部分线性回归模型，结合逆概率加权广义估计方程和Ueki[13]的变量选择思想，提出了一种基于逆概率加权光滑阈广义估计方程(IPW-SGEE)的变量选择方法，其中非参数部分使用样条方法逼近.该方法具有下列3个特点：第一，因为不涉及凸函数最优化问题，所以算法实现相对简便，且获得估计具有Oracle性质.第二，将Ueki提出的光滑阈估计方程方法[13]进行了推广，使其应用到协变量是发散维且响应变量是单调缺失的纵向数据半参数回归模型中.第三，与Wang[11]方法比较，本文方法分析了半参数回归模型.半参数回归模型既具有参数模型的优点，也具有非参数回归模型的优点，因此有更广泛的实际应用价值.

本文首先介绍模型和缺失机制，以及基于逆概率加权光滑阈估计方程的变量选择方法.然后在一些正则条件下研究给出该IPW-SGEE变量选择方法的渐近理论性质，并详细列出获得IPW-SGEE估计的迭代计算算法.最后通过随机模拟研究验证了该方法的有限样本性质.

1 模型和缺失机制

对于高维纵向数据，考虑如下部分线性模型：

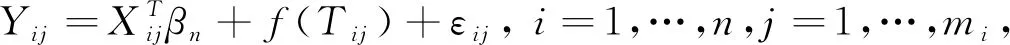
(1)

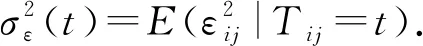
这里考虑响应变量Yij缺失，当Rij=1，Yij可观测；Rij=0，Yij缺失.进一步考虑Yij是单调随机缺失，即当Rij=0时，意味着Rik=0且k≥j.另外假定，对于所有个体初始时刻均可以观测，即Ri1=1(i=1,…,n).对于缺失数据问题一般考虑随机缺失机制，即假定

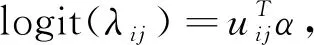
(2)

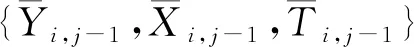
2 IPW-SGEE方法

类似于He等[17]，利用样条回归逼近非参数分量f(·).具体地，设B(u)=(B1(u),…,BL(u))T是阶数为M的B-样条基函数，其中L=K+M，K为内节点个数.B-样条基具有有界支撑且计算稳定[18].节点选择是样条光滑方法中很重要的一个部分，按照文[17]，本文节点的个数取为N1/5的整数部分.f(Tij)可以由B(Tij)Tθ逼近，其中θ∈RL是样条回归系数向量.由此，回归模型 (1)可表示为：

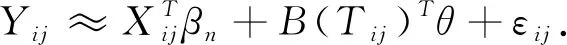
(3)

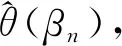
(WTA-1W)-1WTA-1(Y-Xβn),

在单调缺失框架下，按照Robins等[2]的思想，采用逆概率加权广义估计方程(IPW-GEE)方法.具体地，关于βn的IPW-GEE 函数为：

其中Πi=diag{Rij/πij(α),j=1,…,mi}，用于校正由缺失数据造成的偏差.然而，本文的主要目标是同时估计和选择重要的协变量，并且为了避免惩罚估计所带来的非凸函数最优化的问题，基于SEE思想，关于参数βn构造如下的逆概率加权光滑阈广义估计方程(IPW-SGEE)：

(Ipn-Δ)Un(βn,α,ρ)+Δβn=0,

(4)

其中Δ是对角线元素为δ=(δj)j=1,…,pn的对角矩阵，Ipn是pn维的单位阵.注意到，式(4)中第j(j=1,…,pn)个方程，如果δj=1，那么有βnj=0.这就说明式(4)可以得到稀疏解.

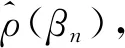
(5)

(6)

3 渐近性质

1)参数向量α是紧集空间Γ上的内点.

2)非参数函数f(·)是r阶可导，其中r≥2.

4)存在正常数c1和c2使得

其中λmin(或者λmax)表示矩阵的最小(或者最大)特征值.

5)对所有的pn，存在正常数c3和c4使得

其中λmin(或者λmax)表示矩阵的最小(或者最大)特征值.

6)P(Rij=1|Yi,Xi,Ti) 有界远离0.

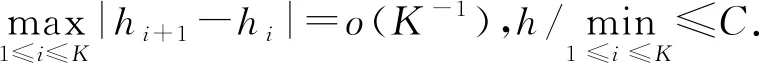
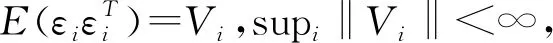
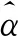
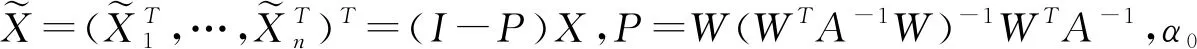
ii)渐近正态性，即

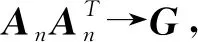
注2定理1和定理2的证明可参见文献[12]和[23].

4 迭代算法

4.1 计算算法

为得到式(6)中参数βn的IPW-SGEE估计，需要得到相关参数α和ρ的相合估计.首先，通过极大似然估计方法得到缺失模型参数α的估计.然后，使用迭代算法估计βn和ρ.按照文[19]，利用校正矩方法估计ρ.定义如下皮尔逊残差

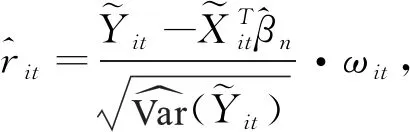
(7)

当相关结构是AR(1)时，工作矩阵R(ρ)的第(t,t+1)个元素的估计为

进而，迭代计算具体步骤如下.

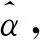
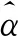
步骤4通过式(8)获得βn的更新估计：

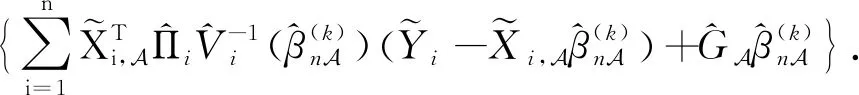
(8)

步骤5重复步骤3～4直到满足收敛条件，并且记最终的估计为IPW-SGEE估计.

4.2 调整参数的选择

使用BIC准则[20]选择调整参数(λ,γ)，其中具体的BIC准则定义如下：

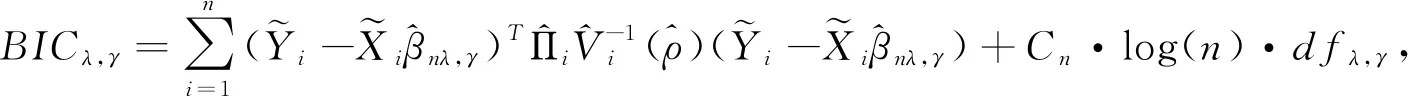
(9)

5 模拟研究

以下主要通过随机模拟实验来验证上文所述逆概率加权光滑阈广义估计方程方法的有限样本性质.产生数据的模型如下：

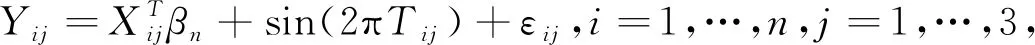
(10)

响应变量Yij单调随机缺失，并且假定每个个体在初始时刻都是可观测的.缺失数据模型为logit(λij)=α0+α1Yi,j-1,其中λij=P(Rij=1|Ri,j-1=1,Yi,j-1)，参数真值α1=-3，α0的真值分别取5和1，相应的缺失比例分别约为26%和40%.

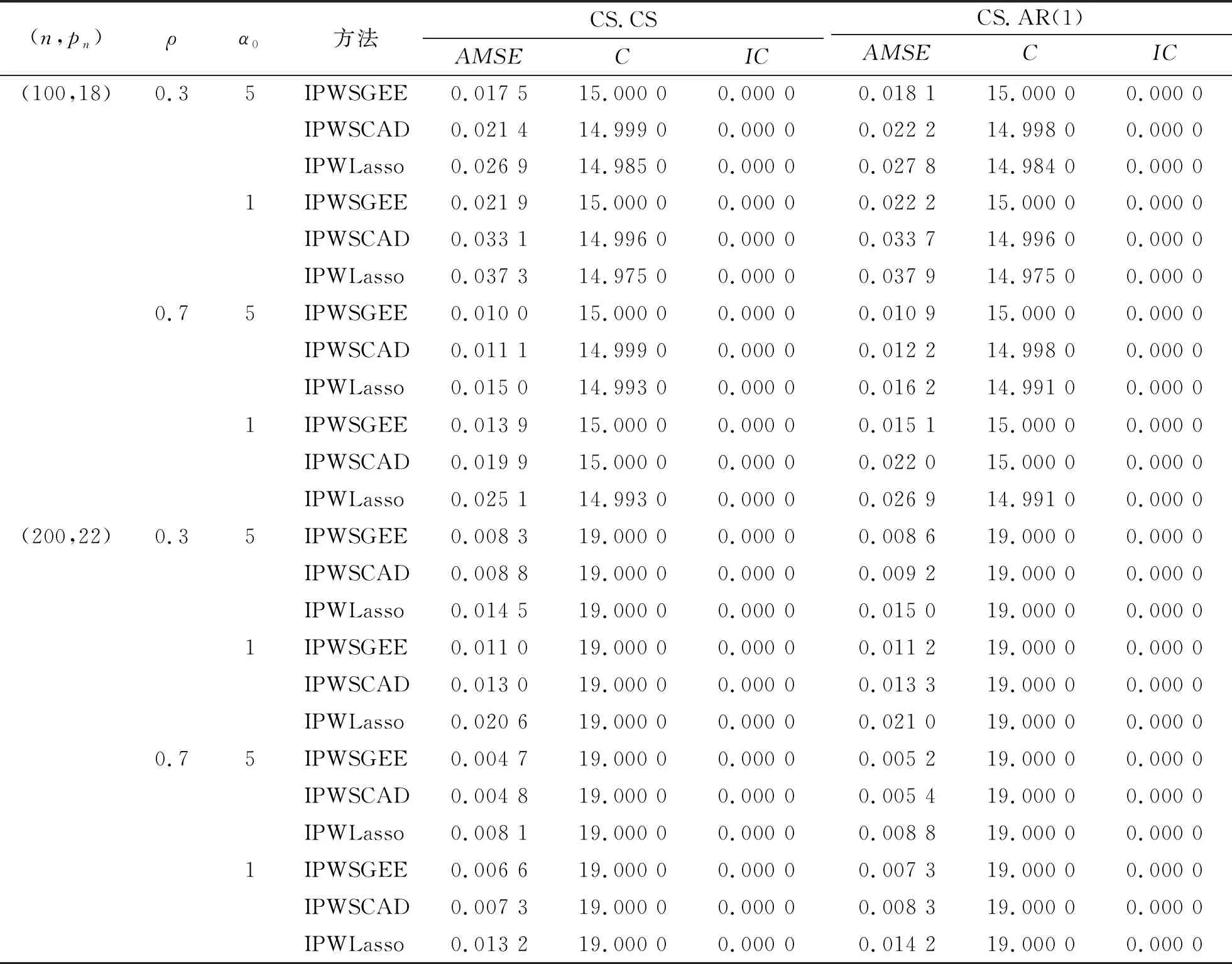
表1 真实相关结构为CS时高维部分线性模型 (10)的变量选择结果Tab.1 Variable selections for high-dimensional partially linear model (10) when the true correlation structure is exchangeable

续表1

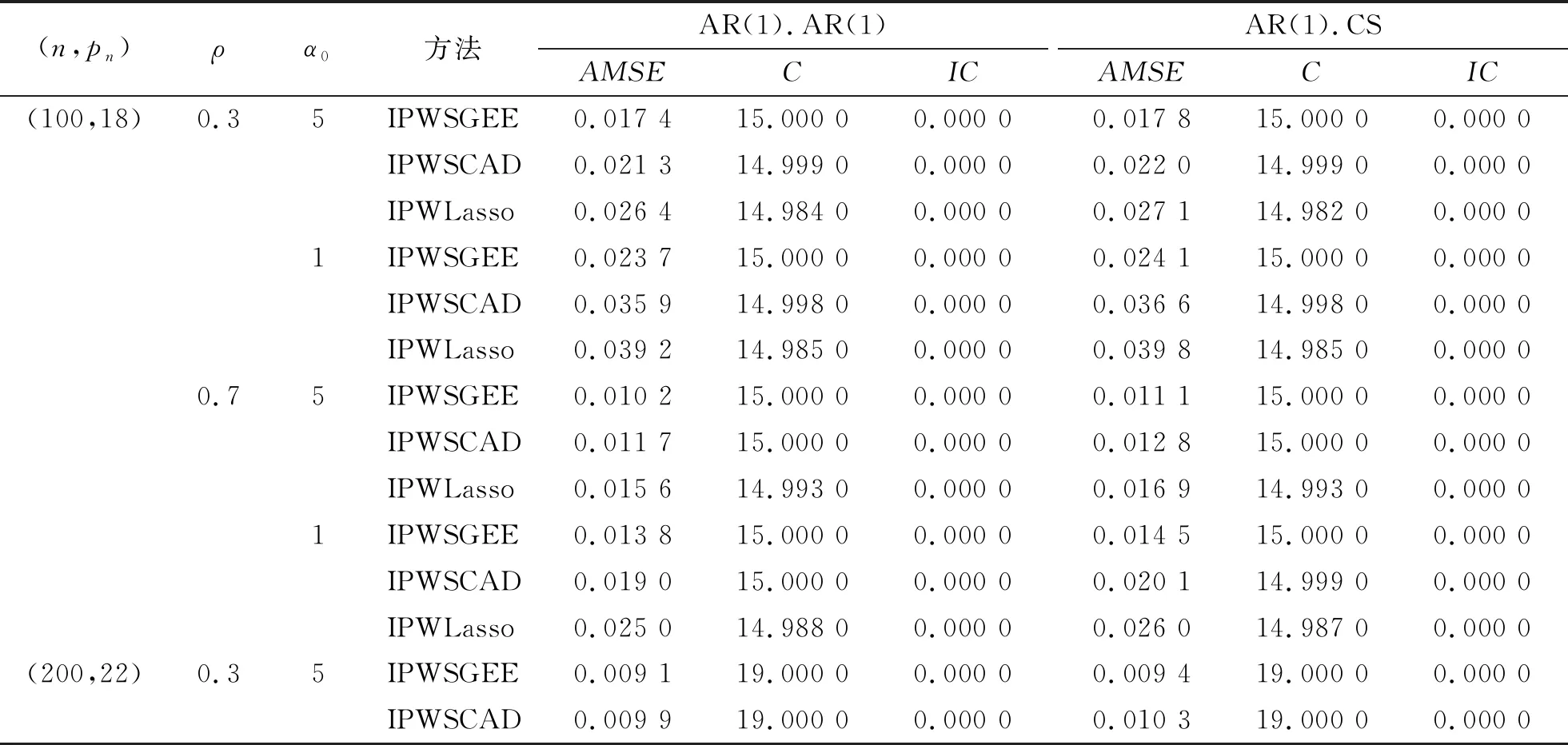
表 2 真实相关结构为AR(1)时高维部分线性模型(10)的变量选择结果Tab.2 Variable selections for high-dimensional partially linear model (10) when the true correlation structure is AR(1)

续表 2

由表1和表2可得：1)即使在错误指定工作相关矩阵下，随着ρ的增大，IPW-SGEE方法的变量选择效果也越来越好.2)随着缺失比例变小，IPW-SGEE、IPWSCAD和IPWLasso这3种变量选择效果也变得越好.另外，与IPWSCAD和IPWLasso方法相比，IPW-SGEE变量选择方法在各个指标方面的表现效果都要较好一些.3)在正确指定相关结构下，IPW-SGEE方法的变量选择效果稍好于错误指定相关结构下的效果.这也说明本文所提出的方法并不显著地依赖工作相关结构.