配置BES型扼流适配变压器的道岔区段轨道电路调整表仿真计算

刘 倡，杨世武，崔 勇，吕佳奇

（1.北京交通大学 电子信息工程学院,北京 100044；2.通号城市轨道交通技术有限公司 研究开发中心,北京 100070）

我国普速铁路站内以97型25 Hz相敏轨道电路为主要制式,多采用BE 型扼流变压器。而随着铁路高速、重载的发展,牵引电流和牵引功率也相应增大,钢轨中不平衡牵引电流干扰危害增加,当干扰达到一定程度时,将会影响轨道电路正常工作,进而给铁路运营带来安全隐患。为有效改善不平衡牵引电流脉冲干扰信号设备的问题,在大秦线2万t重载大电流牵引扩能改造以及客运专线中应用了抗干扰性能优异的适用于ZPW—2000A 轨道电路的BES 型扼流适配变压器（简称扼流适配器）,解决了其适应大牵引电流干扰问题［1］。此外,随着普速铁路的提速和电气化改造,在牵引电流干扰严重的区段,特别是干扰大的道岔区段,也广泛采用适用于25 Hz 相敏轨道电路的扼流适配器替换原BE型扼流变压器［2］。在更换扼流适配器时,无须更改轨道电路本身的系统架构和各信号设备的参数指标,只需更改线路的调整表。采用扼流适配器的调整方法一般参考原有调整表,但由于器材传输特性有差异,且扼流适配器有调整相位功能,因此目前的调整方法难以适应实际设备更换及运营维护的需求。

另一方面,铁路道岔区段的轨道电路采用1 送多受的设置,实现对不同钢轨线路分支的列车占用检查、传递行车信息的作用,常见类型有1 送2 受与1送3受。而既有的文献主要是针对1送1受型轨道电路：齐华基于1 送1 受结构对25 Hz 相敏轨道电路进行了仿真计算［3］；张永贤等通过建模仿真,分析计算了ZPW—2000A 型轨道电路［4］；乔志超等基于矢量匹配法建立不对称高压脉冲轨道电路的宽频仿真计算模型［5］；韦强等通过“两次短路法”完成轨道电路一次参数的测量［6］；田铭兴等通过二端口网络理论建模,分析了无绝缘轨道电路断轨状态的传输矩阵参数及接收端转移阻抗等［7］；赵林海等基于传输线理论提出机车信号感应电压幅值包络仿真模型,并给出基于遗传算法的无绝缘轨道电路故障综合诊断方法［8］。孟景辉等分析了不同载频的区间轨道电路检测数据散点图,并采用线性拟合方法分析了区间轨道电路传输特性[9]；祝林啸等针对新型数字编码轨道电路传输的窄带多音调频信号,提出利用FIR 高通数字滤波器进行多音调频信号数字解调的方法[10]。而对于1 送2 受型轨道电路,相关研究则接近空白。

文献［11］提出了1 送2 受型轨道电路传输参数计算思路,其核心思想是遇道岔分歧处将其他分支连同受端折合成阻抗并联在1 送1 受等效电路上（列车分路时,等效阻抗并联在列车分路的支路上）,进而采用均匀传输线方程法进行各级电压、电流等参数推算,但并未在文中给出具体计算公式和方法。故本文基于该思想,搭建典型站内单开道岔区段1送2受型25 Hz相敏轨道电路的仿真计算模型,该模型综合考虑钢轨阻抗、道砟电阻等参数对轨道电路的影响不同,通过计算带BE 型扼流变压器时轨道电路调整及分路状态参数来验证该模型的准确性；再拓展应用于带扼流适配器的情况,采用该模型完成轨道电路关键参数的仿真计算,得到道岔区段带扼流适配器时1送2受轨道电路调整表,该调整表可用于实际轨道线路中扼流适配器的更换及维护。

1 轨道电路系统构成与仿真计算模型的搭建

对于97 型25 Hz 相敏轨道电路,其道岔区段1送2 受型轨道电路系统由传输电缆、送电端扼流变压器、送电端电源变压器、钢轨线路、受电端扼流变压器（正线及侧线）、受电端中继变压器、防护盒、交流二元二位继电器等设备组成,如图1所示［12］。图中：括号内的字母为对应器件的英文名称；GJZ220和GJF220为送电端电源的2个端子；GJ为轨道继电器；JJZ220和JJG110为GJ的1束局部电源。

图1 道岔区段1送2受型25 Hz 相敏轨道电路系统构成

根据图1,假设机车在正线运行,且分路点在正线接收端至道岔分支处钢轨,可将侧线分支连同其受端折合成等效阻抗并联在电路上,其它单元模块进行四端网结构等效［13］,由此搭建的轨道电路仿真计算模型如图2所示。

图2中：为供电变压器二次测电压；Rx为限流电阻；和分别为送电端扼流变压器信号线圈的电压和电流；为送电端扼流变压器四端网络系数；和分别为轨道电路始端电压和电流；Zg1,Rd1和L1分别为送电端至道岔分支处轨道区段的钢轨阻抗、道砟电阻、距离参数,其中L1为送电端至道岔分支处钢轨长度；和分别为正线轨道电路终端电压和电流；Zj2为侧线受电端等效阻抗；Zg(L2-x),Rd(L2-x),(L2-x)分别为道岔分支处至机车分路点轨道区段的钢轨阻抗、道砟电阻、距离参数,其中L2为道岔分支处至正线接收端钢轨长度；x为机车分路点至正线受电端钢轨长度；Rf为机车分路电阻；Zgx,Rdx,x为机车分路点至正线受电端轨道区段的钢轨阻抗、道砟电阻、距离参数；,为正线受电端扼流变压器四端网络系数；Ry为正线受电端扼流变压器与轨道电压器间的连接电阻；为正线受电端中继变压器四端网络系数；和分别为正线受电端扼流变压器信号线圈的电压和电流；Rl为连接中继变圧器与轨道继电器电缆等效电阻。

图2 1送2受型25Hz 相敏轨道电路仿真计算模型

通过图2中各模块四端网系数可计算得出电路模型中各支路电压、电流,并采用四端网级联的方式（即各模块四端网系数矩阵相乘）,完成该轨道电路系统仿真从受电端到送电端的推算。另外,对并联及串联在电路中的阻抗（分别以Zj2和Rx为例）,其四端网系数矩阵[Aj2Bj2Cj2Dj2]和[AxBxCxDx]与其阻抗的换算关系为

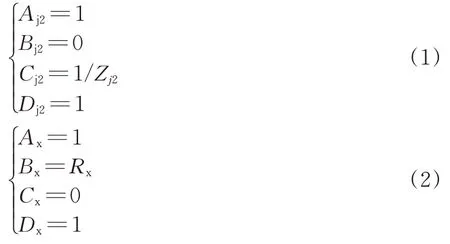
2 带BE时仿真计算及分析验证

2.1 轨道四端网络系数计算

在普速铁路,站内多采用双塞钉式钢轨接续线,25 Hz 相敏轨道电路的钢轨阻抗为0.62∠42° Ω · km-1［14］。道砟电阻的取值,根据《铁路信号维护规则技术标准Ⅰ》［14］的规定,在轨道电路调整状态计算时取最小值0.6 Ω · km,在分路状态计算时取无穷大值∞。在1送2受情况下,由于道岔分支的存在,需将轨道区段分成3段,即①送电端至道岔分支处,②道岔分支处至正线受电端,③道岔分支处至侧线受电端,且3 段轨道的长度L1,L2,L3均取为0.2 km。

以轨道区段①为例,根据传输线方程法［15-17］,求得传播常数γ1和特性阻抗ZK1分别为

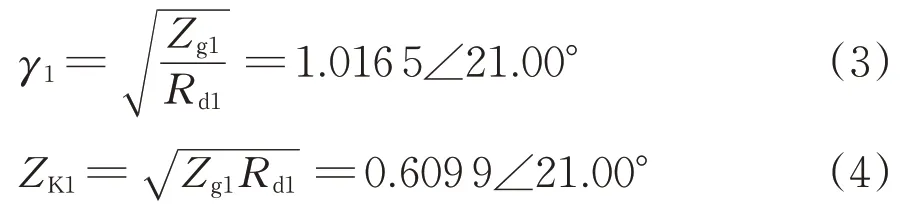
故四端网络系数为

2.2 轨道电路调整状态参数计算

以轨道线圈电流零度相角为基准,从正线受电端开始向前推算,此时道砟电阻取最小值。已知轨道继电器GJ工作电压为15∠70° V,且不考虑相位条件时,当其端电压高于15 V,GJ 吸起,当其端电压低于8.6 V,GJ落下［11］。

轨道继电器至中继变压器间传输电缆的电阻Rl=100 Ω,扼流变压器至轨道变压器间连接线的电阻Ry=0.3 Ω,限流电阻Rx=4.7 Ω。中继变压器选用BG25-130/25 型,扼流变压器选用BE—400/25 型。对系数为A˙,B˙,C˙,D˙的通用四端网络,可通过式（6）所示的传输方程,完成二次侧到一次侧电压及电流的推算。

考虑此时交流二元二位继电器失调角β=-14.35°,调整状态部分参数计算结果见表1。

表1 调整状态部分参数计算结果

2.3 轨道电路分路状态参数计算

为确保铁路信号系统正常运行,1 送2 受轨道区段采用将全部支路的轨道继电器前接点串联的方式来控制轨道复示继电器的动作,且须保证每次分路检查至少有1个轨道继电器可靠落下。以列车在道岔分支处正线钢轨分路情况为例,列车分路电阻Rf=0.06 Ω。此时道砟电阻取最大值。假设列车分路点距正线接收端线路长度为xkm,故整个系统的轨道区段被分为x,(L2-x),L1km共3 段。以x从0开始以dx=0.025 km为步长递增为例展开计算。考虑到列车分路时必须满足轨道继电器可靠释放的条件,即其可靠释放值为工作值的44%,故此时正线钢轨终端电压及电流分别为0.19∠73.93° V、0.36∠41.33° A。

分路时需将受电端到送电端完整轨道区段分3 段处理：分路点至正线受电端、道岔分支处至分路点、送电端至道岔分支处。

考虑失调角β=6.94°,不同列车分路点下分路状态参数计算结果见表2。

2.4 计算结果验证

将上述计算结果与《铁路信号维护规则》［14］对比验证可知,提出的带BE 型扼流变压器的轨道电路仿真计算模型符合1 送2 受型轨道电路电气特性,满足97型25 Hz相敏轨道电路调整表要求。分路状态时,接收端残压最小值大于7.4 V,可保证轨道继电器可靠落下；最不利地点分路灵敏度不小于0.06 Ω,可保证轨道电路可靠分路；各分路点电压余量均大于8.0,说明轨道电路能够正常工作。由此可知,该模型符合现场实际情况,可用于道岔区段1送2受型25 Hz相敏轨道电路的仿真计算。将该模型中的扼流变压器四端网络替换为扼流适配器四端网络,便可将该模型拓展应用到带BES 的轨道电路区段。

表2 分路状态部分参数计算结果

3 带扼流适配器时仿真计算及关键参数特性

3.1 扼流适配器四端网系数测量计算

为解决电气化干扰［18-20］引起的25 Hz 系列轨道电路脉冲干扰导致误动问题,扼流适配器采用大气隙的铁芯,且在信号侧并联适配器。一方面,采用串联谐振与并联谐振的电路特点,实现对50 Hz工频干扰的滤除,避免其进入信号设备；另一方面提高了对25 Hz 信号的传输阻抗［21］。显然,其传输特性与普通扼流变压器也存在差异。

扼流适配器电路如图3所示。主要包括：自耦变压器；Rm与Lm并联构成的等效励磁阻抗电路；理想变比变压器（变比为n）；二次侧等效电路这4 个电路模块［22-23］；漏阻抗ZL。其中二次测等效电路中：L3为次级线圈励磁感抗；L2,C1,C2,R构成谐振电路,实现适配器功能。

图3 扼流适配器电路

现基于BES2型扼流适配变压器展开具体参数计算。通过实测可得到扼流适配器一次侧（信号侧）开路阻抗Z1∞、短路阻抗Z10,以及二次侧（钢轨侧）开路阻抗Z2∞、短路阻抗Z20,其值与扼流适配器四端网络系数换算关系如式（7）所示,根据式（7）即可反推扼流适配器四端网络系数。

以扼流适配器变比为26 为例,根据式（7）可反推得到发送端四端网络系数为=3.914 1∠-9.9°,=5.343 0∠17.1°,=0.192 0∠-17.1°,=0.517 6∠9.9°。计算接收端系数时,可认为电流反向,即变压器一次侧与二次侧交换,故式（7）中Z1∞,Z10,Z2∞应分别用Z2∞,Z20,Z1∞替换,再反推得到接收端四端网络系数为=0.405 7∠9.286 9°,=1.631 7∠11.486 9°,C˙besh=0.150 5∠-17.713 1°,=3.067 6∠-10.513 1°。

3.2 调整表计算

根据图2所示模型,选取钢轨传输阻抗0.62∠42°Ω · km-1,道砟电阻0.6 Ω · km,受电端轨道变压器与扼流适配变压器之间的电缆电阻为RS,限流电阻为Rx（含扼流适配器至供电变压器之间电缆的电阻）,轨道长度L1,L2,L3≤200 m,其他基本线路参数沿用带BE 时的情况。仿真计算得出轨道电路调整表见表3。表中：Ujmin与Ujmax分别为轨道继电器最小与最大端电压,即交流二元二位继电器轨道线圈上电压的计算分别对应道砟电阻为最小值及最大值的2种情况［24］；Ucan为机车分路时轨道电路接收端残压,即标准分路电阻在轨面分路时轨道继电器端电压［25］。

表3 带扼流适配器轨道电路调整表

Ucan值可由图4所示模型与式（8）计算,图4中：四端网络系数Acan,Bcan,Ccan,Dcan为分路电阻后级至轨道继电器GJ 前级的等效四端网络矩阵的乘积；Uf为分路电阻Rf两端电压；Ican为GJ前级输入电流。

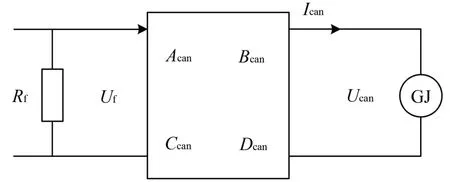
图4 分路残压计算模型

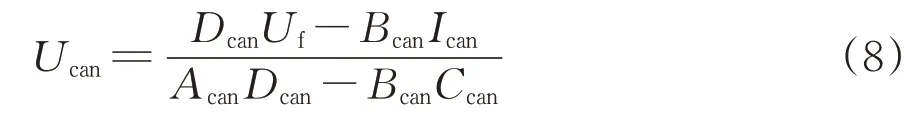
经计算,本例中轨道电路分路残压值均不超过7.4 V,符合标准规定的97 型轨道电路接收端残压值不应大于7.4 V。故得到的调整表可应用于带扼流适配器时1送2受型轨道电路。

3.3 分路灵敏度计算及分析

分路灵敏度是轨道电路中引起分路效应时的最大分路电阻值,记为βlm,其用阻值的形式表示［26］,即

式中：与分别为分路状态与调整状态时发送端供电变压器电压。

为保证轨道电路可靠分路,要求线路分路最不利点的分路灵敏度不小于0.06 Ω。为此,选取分路步长为25 m,遍历分路点,采用上述模型和式（9）,仿真计算不同分路点距接收端距离时的分路灵敏度,结果如图5所示。由图可知,轨道各处分路灵敏度均大于0.06 Ω,符合轨道电路可靠分路的要求。

图5 不同列车分路点下的分路灵敏度

观察图5中曲线的变化趋势,显然曲线在道岔分支处出现转折,说明道岔分支处是该线路条件下分路最不利点。该结果与文献［11］中无受电分支情况下1 送2 受型轨道电路区段分路最不利点在岔尖处的结果相符,但与传统1 送1 受型轨道电路区段分路最不利点在接收端或发送端不符。其主要原因在于：道岔设置尖轨及辙叉等结构,存在有害空间,易出现“挤岔”、“四开”等故障［27］；岔区采用道岔跳线和道岔绝缘的设置实现1 送2 受型轨道电路基本功能；通过接续线的设置实现道岔各组成单元间轨缝的电气连接,岔尖处跳线与轨缝设置则更为复杂,列车分路时钢轨中电流存在多条支路；道岔尖有害空间处各钢轨支路并未实际连通,而是利用跳线的设置构成电流通路,而列车分路是依靠轮对接触钢轨表面实现,从而导致列车不易有效分路。综上所述,道岔岔尖是1 送2 受型轨道电路区段中最易导致分路不良的机械环节。

3.4 轨道继电器工作电压余量比

轨道继电器工作电压余量比K的计算公式为

式中：UFmin为最小分路电压；UB为调整电压,即按轨道继电器工作电压为15 V 时计算出的供电电压值［11］。

为确保列车分路时轨道继电器可靠落下,要求供电电压满足列车在分路最不利点的电压余量比不小于8.0。为此,采用上述模型和式（10）,仿真计算各分路点的电压余量比。结果表明,该线路条件下最小电压余量比均大于8.0,可判定各分路点电压余量比均满足轨道继电器可靠工作的要求。

3.5 不同道砟电阻时调整表计算

轨道电路调整表的配置是根据各条线路固定参数来计算的。然而,轨道电路的实际工作环境会随着自然环境条件的变化相应发生改变。尤其是道砟电阻作为轨道电路的一次参数,其变化特性十分复杂。道砟电阻的等效值与多种因素有关,在实际铁路现场中,由于道砟材料、道砟层的厚度和清洁度、轨枕的材质和数量、路基和土壤的导电率、气候等的变化［28］,导致不同线路的道碴电阻不同。故针对不同线路条件,选取不同的道砟电阻Rd［29］,采用上述模型,仿真计算不同道砟电阻时轨道电路调整表,结果见表4,表中分路残压Ucan为其计算结果的最大值。

表4 不同道碴电阻情况时的调整表

由表4可知：计算结果满足调整和分路状态标准要求；随着道砟电阻的增大,轨道电路正常工作所需发送电平减小,轨道继电器最大端电压下降,轨道继电器最小端电压增加,分路残压下降。显然,道砟电阻的增大,使得轨道电路可允许发送电平适度降低,且更有利于列车分路。

4 结 论

（1）提出了一种应用于站内道岔区段1 送2 受型轨道电路的仿真计算模型,并基于现场实测的带BE 型扼流变压器的轨道电路一次传输参数,对轨道电路调整和分路状态下发送电压和电流的模拟计算,结果反映了1 送2 受型轨道电路的工作特性,符合现有调整表要求,从而验证了该模型的正确性和有效性。将该模型中的扼流变压器四端网络替换为扼流适配器四端网络,便可将该模型拓展应用到带BES的轨道电路区段。

（2）结合扼流适配器传输特性,实际测量并计算了其四端网络系数；采用拓展的模型仿真计算,得到带扼流适配器轨道电路在1 送2 受区段的调整表；同时计算分析该轨道电路区段的分路灵敏度和电压余量比可知,分路最不利点的分路灵敏度满足不小于0.06 Ω的要求,且道岔岔尖是1 送2 受型轨道电路区段中最易导致分路不良的机械环节；最小电压余量比均大于8.0,故各分路点电压余量比均满足轨道继电器可靠工作的要求。

（3）采用该拓展模型仿真计算得到不同道砟电阻时的调整表。道砟电阻的增大,使得轨道电路可允许发送电平适度降低,且更有利于列车分路。

（4）该模型可用于实际线路更换扼流适配器后轨道电路调整表的编制,以及轨道电路维护及优化时调整表的计算。同时,该模型也可拓展应用于三开、复式交分等道岔区段以及ZPW—2000A 型等其他制式轨道电路调整表的计算。