高速铁路840m全封闭声屏障气压荷载数值模拟研究
2020-06-10何旭辉郭柯桢葛辉凯敬海泉
何旭辉,郭柯桢,杨 斌,葛辉凯,敬海泉
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中南大学 高速铁路建造技术国家工程重点实验室,湖南 长沙 410075;3.中国国家铁路集团有限公司,北京 100844;4.雄安高速铁路有限公司,河北 保定 071700)
随着高速铁路运行速度的进一步提升,噪声污染这一问题愈发突出。目前,多采用设置声屏障的手段降低噪声对周边环境的影响。为满足不同的降噪要求,一般结合工程实际等多方面因素进行声屏障结构形式选型[1]。在声环境要求较为严苛的地段,如居民聚居区和生态保护区,多采用全封闭声屏障这种结构形式,它能够显著降低环境噪声污染,但是由于其形成的相对封闭空间使内部气流的流动性受限,导致列车高速通过时会产生强烈的活塞风效应,使得声屏障内部气压荷载会迅速增加,对声屏障结构的强度和稳定性是极大的考验[2]。
国内外的许多专家学者对列车的脉动风压特性进行了研究,并取得了一定的成果。Baker[3]为描述列车周围流场性质,利用试验和计算的结果,对列车在开阔场地中的静风状态下和横风作用下的气动特性分别进行探讨。Rabani[4]验证不同的车头形状对隧道出口压力传感器的影响,并与已有研究成果对比,从而验证数值模拟的可行性,并证明了阻塞率和速度对第1 个压力波的影响;Chen[5]模拟350 km·h-1高速列车通过典型的双线隧道,讨论头车变化段长度对隧道壁面气压荷载的影响;龙丽平[6]基于流体计算软件CFX 探究列车经过直立式声屏障时的空气脉动力分布规律;Zhang[7]选用RNGk-ε湍流模型,模拟高速列车进入隧道时的气压荷载分布,并探讨隧道入口斜率对列车表面压力的影响;韩珈琪[8]利用Fluent 动态铺层技术,模拟作用在声屏障上的气压荷载特性,并对不同形式声屏障的气压荷载进行讨论;骆建军[9]通过滑移网格技术,计算得出隧道内的压缩波呈现三维特性,且同一断面上的压力变化差异性与列车的运行方式有关;余南阳[10]计算流线型列车及隧道主要参数对环状空间3 s 内最大压力变化的影响;李新华[11]着重分析列车驶入隧道的流动方程,在时间和空间尺度得出不同时刻的流场状态。此外,刘堂红[12]采用实车试验的方法,探究出隧道内列车风风速与列车运行速度呈线性关系;何德华[13]也进行了一系列隧道单列列车通过和2 列列车交会的实车试验,总结了压力波随车速、车长和隧道长度等影响因素变化的规律。
尽管高速铁路全封闭声屏障结构形状与隧道结构类似,既有隧道空气动力学的研究结果对全封闭声屏障气压荷载具有参考意义;然而,由于声屏障质量更轻、结构更柔,全封闭声屏障对列车风荷载更加敏感,既有隧道空气动力学研究结果无法满足全封闭声屏障结构设计要求。
本文以我国高铁线路某全封闭声屏障为研究对象,建立流固耦合数值计算模型,对高速列车以350 km·h-1速度通过全封闭声屏障(单车和会车)时产生的气压荷载进行系统研究,分析并总结气压荷载的分布规律及极值,可为全封闭声屏障设计提供理论依据。
1 数值计算原理及模型建立
1.1 标准k-ε两方程湍流模型
基于RANS 方法,根据文献[14]的研究结论,选用准确、高效、适用性强的标准k-ε两方程湍流模型进行流场和气压荷载数值模拟,为

其中,
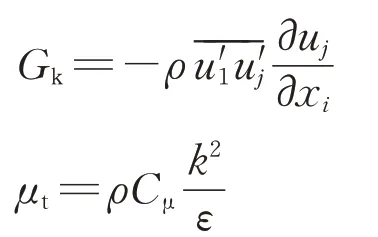
式中:ρ为空气密度;k为湍流动能;t为时间;ui和uj为列车周围流场速度;为空气压力黏度;ε为湍流耗散率;xi为坐标的三分量;μt为涡黏性系数;Gk为湍流动能基于平均速度梯度得到的增项;Gb为基于浮力产生的湍流动能增项,本文可忽略此项;G3ε为与浮力相关的常量,可忽略;G1ε,G2ε为常量;σk和σε为与k和ε对应的普朗特数,在标准k-ε两方程湍流模型中分别为1.44,1.92,1.00,1.30;Cμ为常量,取0.09。
1.2 移动网格的设置
采用Fluent软件中的动态铺层技术实现列车相对于声屏障运动的数值模拟,这种方法将计算域分为动网格和静网格区域,其中动网格区域包含列车车体和车体周围的流场,静网格区域包含声屏障在内的外部流场,动静网格之间设置Interface 的数据交互面进行数据传递。在运动过程中,动网格区域发生“坍塌或合并”,静网格区域则不进行网格重构;此方法可减少计算量,提升计算效率。动网格发生坍塌时和合并时的条件由交界面处的单元高度决定,坍塌高度h1和合并高度h2的计算公式分别为

式中:ac为坍塌因子,取0.2;hconstant为划分的动网格高度,取1 m;as为分裂因子,取0.4。
1.3 数值模型建立及网格划分
采用我国高速铁路开行的复兴号动车组,选择8 列编组建立列车数值模型如图1所示。基于计算机性能和计算效率等多重因素考虑,对数值模型进行了适当简化,忽略转向架、车门、受电弓等构件对气动外形的影响,并对列车表面进行光滑处理。

图1 列车模型示意图
建立全封闭式声屏障数值模型如图2所示,其断面面积为110.5 m2,由骨架立柱、横梁、纵向连接系、单元板等组成。数值建模时对声屏障的表面进行了平滑处理和适当简化。骨架立柱为H 型钢,其内部翼缘板距声屏障面板50 cm,一定程度上减小了声屏障的净空面积。为了更精确化地模拟列车在声屏障中高速运行引起内部的气压变化情况,数值模型考虑了H 型钢立柱对声屏障内部空间外形的影响。

图2 全封闭声屏障模型示意图
在ICEM 数值模拟软件中建立列车和声屏障流体力学计算模型。模型计算域分为3个部分,具体尺寸如图3所示,中间部分为全封闭声屏障计算域,共长840 m,两端为列车加/减速的过渡段计算域,长550 m;所有计算域的宽度和高度均为50 m。加/减速区计算域的长度能够保证列车充分加/减速,同时不因气压急剧变化而产生误差[15]。由于H 型钢立柱的存在,声屏障内壁外形复杂,中间计算域采用非结构化网格,2 端的加/减速计算区域采用结构化网格。为了减小列车移动对边界条件造成影响,列车初始位置设置在声屏障外、距其边界200 m处。

图3 计算域尺寸示意图
计算域的侧面和顶面都采用压力出口边界,地面、列车以及声屏障采用无滑移边界条件,计算域3 个部分之间采用内部界面interior,动、静网格区域之间采用interface 的数据交换界面,各计算边界示意图如图4所示。
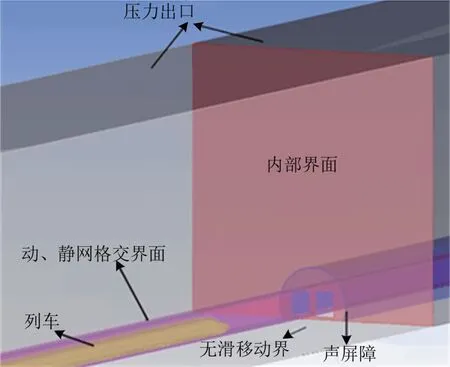
图4 计算边界设置示意图
为了更详细地捕捉到边界层附近的流体运动情况,提高模拟精度,在声屏障面板附近以及靠近列车区域的网格加密,而远离列车和声屏障的外部区域,网格适当稀疏,从而最大程度上节省计算成本,提高计算效率。经过一系列的网格无关性试算后,最后确定地面网格最大尺寸为0.1 m,列车表面网格最大尺寸为0.2 m,声屏障表面网格最大尺寸为0.3 m,全局网格最大尺寸为1 m,总网格数为2 400万个,网格划分情况如图5所示。

图5 网格划分示意图
1.4 监测内容及测点布置
通过在声屏障壁面上布置测点进行气压监测,可以得到不同时刻下、相应位置处的气压荷载变化规律及极值大小。同时,在列车的鼻尖及车尾处设置监测测点,用以研究列车在进入声屏障且2 列列车相会时鼻尖处的空气压力变化,一方面可以研究列车自身稳定性问题,另一方面也可以与声屏障上空气压力时程进行相互对照,证明模拟的可行性和准确性。
全封闭声屏障各测试截面的示意图如图6所示。根据隧道空气动力学的研究经验,当2 列列车交会时,中间测试截面气压荷载最大;因此,在声屏障中间测试截面⑥的左右两侧对称设置间距较小的测试截面⑤和测试截面⑦;再往洞口方向依次间距50,100,100 和110 m 对称设置测试截面,共设置11 个测试截面。每个测试截面上依据等距再设置11个测点,如图7所示。

图6 全封闭声屏障测试截面编号示意图

图7 测试截面测点分布示意图
2 模拟结果
2.1 单车工况下声屏障气压荷载
通过对单列列车以350 km·h-1速度通过840 m全封闭声屏障的列车风场模拟,获得各测点气压时程曲线。由于靠近全封闭声屏障2 端测试截面上的气压荷载分布规律和气压荷载极值(简称压力极值)均十分接近,因此展示除测试截面②和测试截面⑩以外的9个测试截面的气压荷载计算结果,如图8所示。由图8可见:由于压力波在全封闭声屏障内部纵向传播,同一测试截面不同测点处的气压荷载保持相似的波动规律,不同测试截面的气压荷载变化规律存在显著差异;同一截面上不同测点的压力极值各不相同,说明单列列车经过时,全封闭声屏障各截面气压非均匀分布,极值压差达到0.6 kPa。
由图8还可见:靠近声屏障出入口测试截面的气压波动更为复杂和无序,压力极值持续时间较短,而在靠近声屏障中间位置的测试截面的气压荷载波动更加规律,且呈现明显的周期性,达到气压荷载峰值持续时间较长;随着测试截面距声屏障入口距离的增加,气压荷载达到极值的时间变长,这是由于列车导致的气压波在声屏障内部传播所致;对称测试截面(如测试截面①和测试截面⑪,测试截面③和测试截面⑨等)气压荷载呈现相似的波动规律。

图8 单车工况下各截面测点气压荷载时程曲线
2.2 会车工况下声屏障气压荷载
当2 列列车同时以350 km·h-1的速度相向驶入全封闭声屏障,并且在声屏障1/2 跨会车时,各测试截面的气压荷载随时间变化规律如图9所示。由于列车运行状态和结构的对称性,仅展示测试截面①至测试截面⑥的气压荷载时程。由图9可见:1/2 跨会车工况气压荷载与单车工况气压荷载呈现出部分相似的规律,即相同测试截面各测点的气压波动规律保持一致,不同测试截面则不相同;靠近声屏障入口测试截面的气压荷载波动更为复杂和无序,而在靠近声屏障中间位置测试截面的气压荷载的波动更加规律,且呈现一定的周期性;同一测试截面各测点的气压荷载并不完全一致;同时,1/2跨会车工况气压荷载与单车工况气压荷载也存在明显差异:1/2 跨会车工况下各测试截面的气压荷载波动变得会更加复杂,出现更多的正压/负压峰值,这是由于更复杂的气压波传递现象以及2 列列车经过测点引起;由于气压波的叠加效应,声屏障中间的测试截面⑥的正、负压力极值最大,为结构最不利截面。
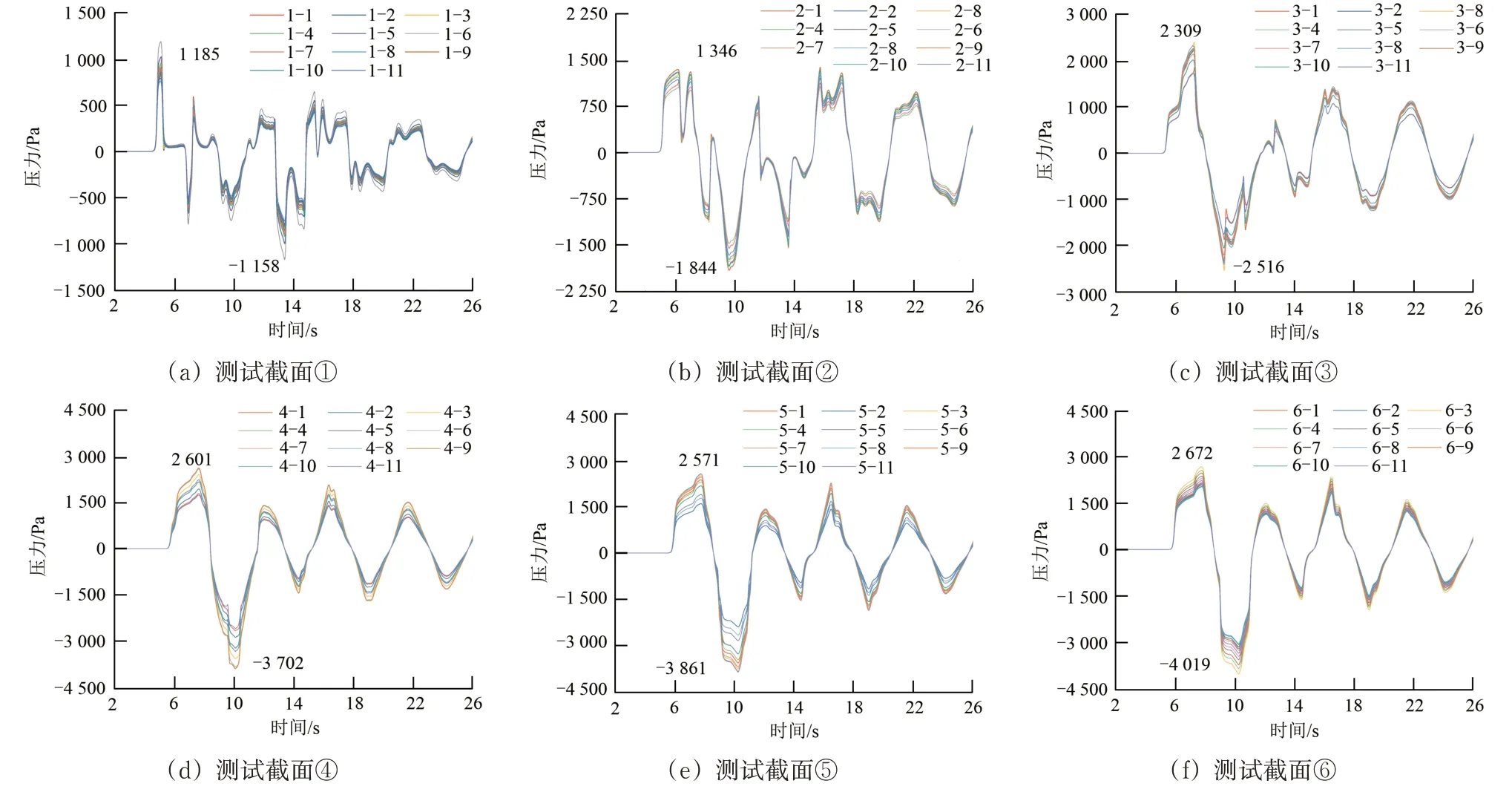
图9 1/2跨会车时典型截面测点气压荷载时程
2列列车在声屏障1/4跨会车时,6个典型测试截面(分别为声屏障入口出口的测试截面①和测试截面⑪,1/4 跨附近的测试截面③和测试截面⑨,以及出现压力极值最大值的测试截面④和中间测试截面⑥)的气压荷载时程如图10所示。由图10可见:1/4 跨会车工况各测试截面的气压荷载与单车工况和1/2 跨会车工况的气压荷载相比,存在部分相似的变化规律,但是差异更加明显。例如,在交会位置附近的测试截面③,气压荷载的变化更加复杂,存在多次气压突升和突降现象,这是由于2 列列车分别进入声屏障时产生的气压波在声屏障内部往返传播所致,气压波往返运动过程中与现有气压叠加容易出现正/负压力极值。
2.3 单车和会车工况下声屏障气压荷载极值
通过对列车以时速350 km·h-1的速度单车通过840 m 全封闭声屏障,以及在1/2 跨和1/4 跨会车的数值模拟研究,得到3种工况下各测试截面的最大正压、负压。根据各测试截面离声屏障入口的距离得出各工况下声屏障展向的压力分布,如图11和图12所示。由图11和图12可见:会车工况各测试截面的气压荷载都大于单车工况;而且1/2 跨会车工况的气压荷载大于1/4跨会车工况;单车和1/2跨会车工况时压力极值都出现在中间测试截面[16],而1/4跨会车工况压力极值则出现在1/4跨附近的测试截面④;1/2跨会车工况压力极值最大,最大正压为2 672 Pa,最大负压为-4 019 Pa,单车工况时最大正压为1 305 Pa,最大负压为-2 154 Pa。
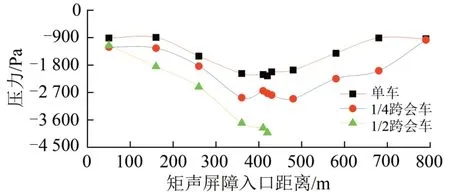
图12 会车和单车工况各测试截面最大负压
3 种工况下压力幅值沿轴向的分布规律如图13所示。由图13可见:3种工况下,压力幅值分布规律与最大正压和最大负压分布规律十分相似,均呈现由中间向两端递减的趋势;而且会车工况下各测试截面压力幅值均大于单车工况下;在声屏障出入口附近测试截面,1/2 跨会车和1/4 跨会车的压力幅值基本相等;1/2 跨会车时,最大压力幅值出现在中间测试截面,而1/4 跨会车时,最大值出现在交会位置附近的测试截面④;而且1/2 跨会车工况的最大压力幅值高于1/4 跨会车工况的最大压力幅值;1/2 跨会车工况最大压力幅值为6 691 Pa,1/4跨会车工况最大压力幅值为5 032 Pa,单车工况最大压力幅值为3 459 Pa,1/2 跨会车工况下最大压力幅值为1/4跨会车工况的1.33倍、为单车工况的1.93倍。
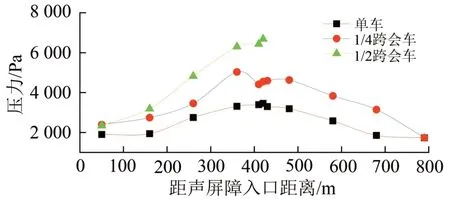
图13 会车和单车工况各测试截面压力幅值
3 结 论
(1)所有工况下全封闭声屏障中间位置的气压荷载都大于靠近出入口位置的气压荷载。
(2)1/2 跨会车和单车工况下,都是中心截面的压力极值达到最大,而1/4 跨会车时压力极值在靠近会车位置的截面出现最大值。
(3)1/2 跨会车最大正压和负压分别为2 672和4 619 Pa,分别为单车工况的2.05 倍和1.87 倍,压力极值均大于单车工况,且最大负压极值大于最大正压极值;会车时最大压力幅值达到8 864.7 Pa,为单车工况的1.93 倍。因此,会车工况为较危险工况,应该以此为设计的控制荷载。
(4)不同位置会车对于全封闭声屏障压力极值影响显著,最大压力幅值出现在交会截面附近的测试截面,而且1/2跨会车工况最大压力幅值约为1/4 跨会车工况的1.33倍。
