考虑车轮谐波磨耗的动车组车轴疲劳寿命

吴 丹，丁旺才，商跃进，李化明

（1.兰州交通大学 机电工程学院,甘肃 兰州 730070；2.中车唐山机车车辆有限公司,河北 唐山 063035）

随着高速列车运行速度的不断提高,轮轨间各种随机激励引起的轮轨振动加剧。为保证列车安全平稳运行,作为列车主要承载部件的车轴,它的性能良好与否直接关系到列车的行车安全。因此,国内外学者关于车轴疲劳寿命做了大量的研究工作,并取得了一定的成果。田合强等［1］以中国某型高速动车组车轴为研究对象,分别基于日本JIS E 4501 标准和欧洲EN 13104 标准对车轴强度进行计算,并与有限元仿真计算结果进行对比分析。陆超等［2］分别基于欧洲EN 13104 标准和有限元法对出口哈萨克斯坦的动车组动力车轴进行应力计算,并校核各截面处的疲劳强度。随着对车轴强度研究的不断深入,国内外学者［3-5］认为车轴的疲劳强度不能按无限寿命设计和计算,因为对于车轴这类高周疲劳构件,其疲劳强度会随着应力循环次数的增加而降低,计算应力时应考虑各种随机激励的影响。于是,国内外学者开始借助于有限元软件和动力学软件,并结合有限寿命理论进行车轴疲劳寿命的估算,其研究成果具有很高的工程应用价值。如赵利华等［6］运用SIMPACK 软件建立多刚体车辆动力学模型,结合ANSYS 软件计算车轴危险点的应力时间历程,基于线性累积损伤理论计算车轴的疲劳寿命。曹建国等［7］运用SIMPACK 软件建立动车组整车动力学模型,并计算车轴的载荷时间历程,结合ANSYS 和FE-SAFE 软件计算车轴的疲劳寿命。POKORNÝ P 等［8］对实测载荷时间历程下车轴的残余疲劳寿命进行了研究。

随着高速列车车轮多边形问题的日益凸显,尤其是德国ICE高速列车脱轨,研究表明事故的原因是由于多边形橡胶弹性车轮的接触载荷过大、导致车轮轮辋疲劳断裂造成的［9］,引起了众学者的高度关注。之后,对车轮多边形最主要表现形式的车轮谐波磨耗的研究众多,但大部分皆为车辆—轨道耦合动力系统下的振动特性研究,鲜有车轮谐波磨耗下车轴疲劳寿命的研究。然而,在研究构架和齿轮箱时有学者考虑了车轮谐波磨耗因素的影响。如FU Delong 等［10］针对B 型地铁构架出现的疲劳裂纹,运用实测和仿真相结合的方法,发现由于车轮谐波磨耗引起的轮轨振动激发了构架的固有模态,产生高频共振,最终导致疲劳裂纹的发生。WU HAO 等［11］通过建立基于柔性轮对的刚柔耦合车辆动力学模型,分析考虑车轮谐波磨耗因素下的齿轮箱动应力,并对比研究车轮谐波磨耗对齿轮箱壳体疲劳损伤的影响。因此,载荷时间历程作用下考虑车轮谐波磨耗的车轴疲劳寿命研究具有重要的理论意义和工程应用价值。

本文以CRH380BL 型高速动车组为研究对象,通过多体动力学软件UM 建立4 种不同轮轨关系的车辆—轨道耦合动力学模型,对比分析4种轮轨关系下的车辆系统动态响应,得到最能反映真实情况的轮轨关系,然后基于ANSYS,UM 和FE-SAFE软件以及疲劳损伤容限理论联合分析考虑车轮谐波磨耗下的车轴疲劳寿命。

1 车轮谐波磨耗测试

采用中德合资NSH-CTI 公司生产的U2000-G400 型不落轮机床对CRH380BL 型动车组的车轮进行谐波磨耗测试,该设备用于列车在整列编组不解体的情况下,对轮缘和踏面进行在线加工及车轮谐波磨耗在线测试,其测试方式为接触式直接检测。根据其相关操作要求进行车轮谐波磨耗测试,测试现场如图1所示。

图1 车轮谐波磨耗测试现场

测量时,由轮缘顶部自内向外测量,在车轮廓形上滑移的同时,保持磨耗测量头始终与轮对接触。经测试,得到了镟修后17.9万km 的车轮谐波磨耗的实测结果,实测结果表明头车和尾车的车轮谐波磨耗最严重,故将头车车轮谐波磨耗的实测结果通过HHT—希尔伯特黄变换处理得到车轮谐波磨耗阶次图如图2所示。由图2可以看出,头车8个车轮在第20 阶均出现了粗糙度幅值明显增大,表明车轮谐波磨耗主要是由第20 阶主导的。统计发现,该车出现20 阶车轮谐波磨耗主要与轴距和轨道有关。受篇幅所限,此处仅列出头车即第1节车的车轮谐波磨耗阶次图。因此,在实际仿真计算中,可以将实际谐波磨耗处理成由20 阶主导的单一谐波激励。

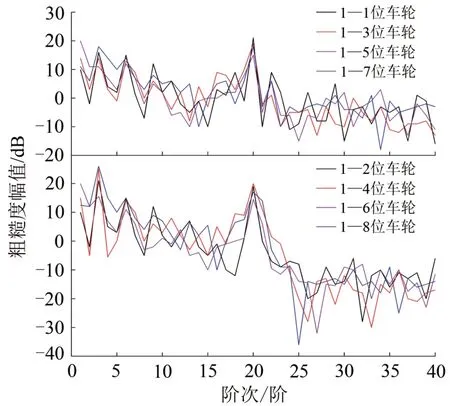
图2 头车车轮谐波磨耗阶次图

2 车辆动态响应对比

2.1 车辆—轨道耦合动力学模型

轮对柔性化时,常用的方法是将轮对模型进行有限元离散,采用模态综合法获得轮对的主要振型。根据CRH380BL 型动车组动力轮对的几何尺寸参数,建立动力轮对的有限元模型,如图3所示。模型离散化时采用4节点Shell63壳单元和8节点Solid185 三维实体单元,以恒定角步长沿Y轴（车轴轴向方向）旋转扫掠划分网格,网格大小为10 mm,通过Contact Pairs 创建轮轴面—面柔性接触对,且根据TB/T 1718.3—2018《机车车辆轮对组装第3部分：动车组》［12］规定的轮轴过盈量取值范围（0.198～0.357 mm）,取其为0.2 mm,接触时的摩擦系数取0.2。车轴材料为EA4T,弹性模量为205 GPa,密度为7 850 kg·m-3,泊松比为0.3；车轮材料为ER8,弹性模量为205.9 GPa,密度为7 850 kg·m-3,泊松比为0.3。在车轴中心线两侧与一系悬挂装置对应处分别添加1个mass 21单元的界面节点,用以模拟轮对的力元连接点,并将界面节点通过约束方程与表面的受力节点相连,利用UM软件中的柔性模块FEM实现柔性轮对的导入,基于UM_ANSYS接口程序通过Craig-Bampton算法求解轮对的主要模态,计算结果见表1。

建立刚性轮轨、刚性轮柔性轨、柔性轮刚性轨以及柔性轮轨共4种轮轨关系下的车辆—轨道耦合动力学模型,以研究4种轮轨关系下的车辆系统动态响应,得到最能反映真实情况的轮轨关系。其中,柔性轮轨关系下的车辆—轨道耦合动力学模型如图4所示。

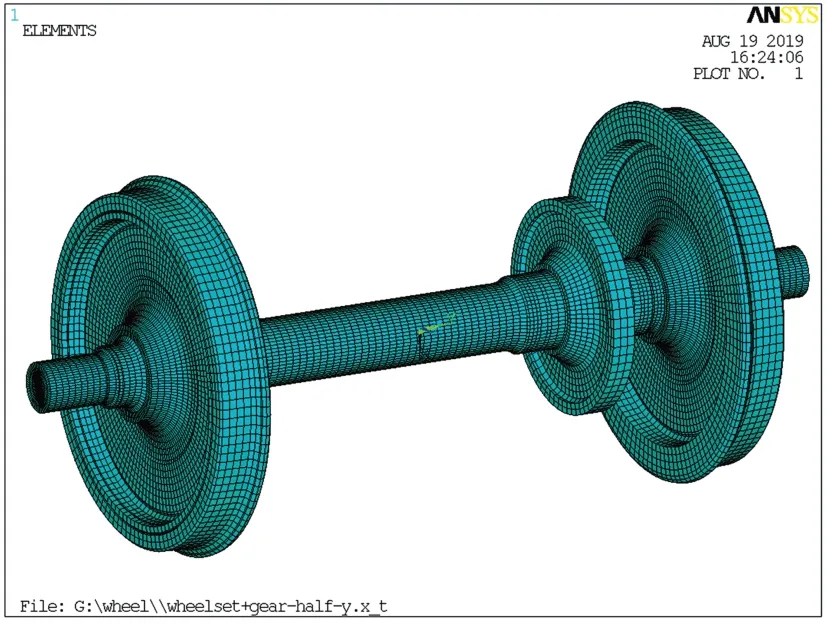
图3 轮对有限元模型

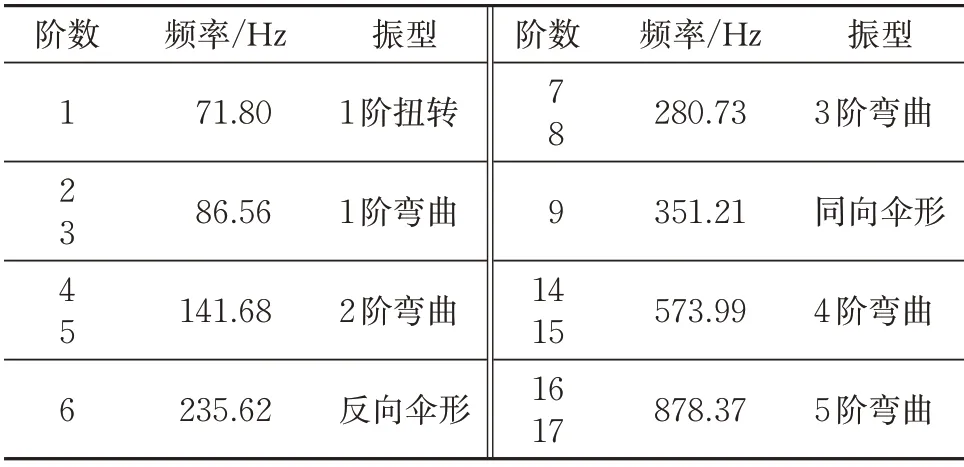
表1 轮对的主要模态

图4 柔性轮轨关系下车辆—轨道耦合动力学模型

2.2 车轮谐波磨耗下的轮轨动态响应

设定车速v为300 km·h-1,车轮谐波磨耗阶数为20阶,幅值为0.05 mm。以我国TB/T 3352—2014《高速铁路无昨轨道不平顺谱》作为轨道激励,得到1位轮对左轮的轮轨垂向力频域图（图5）和时域图（图6）。

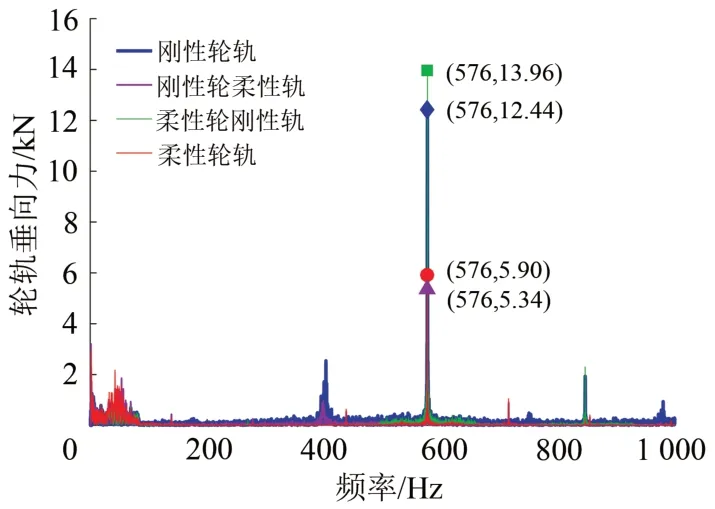
图5 不同轮轨关系下轮轨垂向力频域图

车轮谐波磨耗产生的轮轨激励频率f可通过式（1）进行计算,为

式中：N为车轮谐波磨耗阶数；D为车轮滚动圆直径,为920 mm。

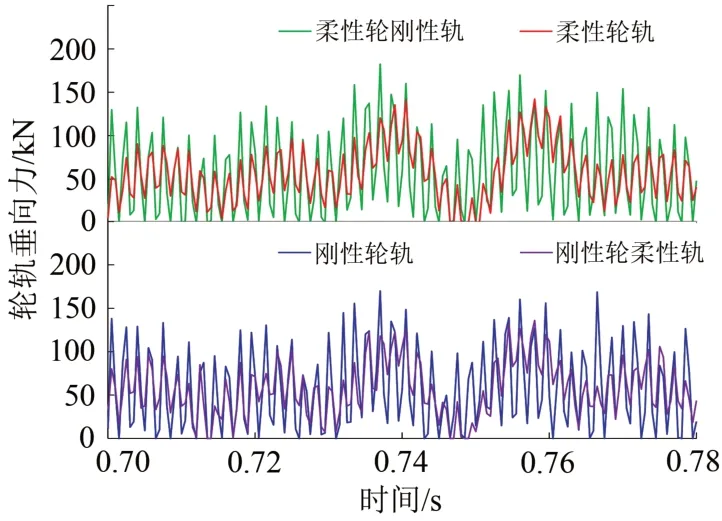
图6 不同轮轨关系下轮轨垂向力时域图

由式（1）计算可得,20 阶车轮谐波磨耗产生的轮轨激励频率为576 Hz。由图5可知,4 种轮轨关系下轮轨垂向力均在576 Hz 附近出现最大值,仿真结果与计算结果一致,验证了模型的准确性。结合图5和图6,进一步分析4 种轮轨关系下的动态响应可知：刚性轨下,刚性轮和柔性轮的轮轨垂向力最大值分别为169.89 和182.37 kN；柔性轨下,刚性轮和柔性轮的轮轨垂向力最大值分别为135.94 和142.15 kN。由此发现：轨道相同时,柔性轮下的轮轨垂向力大于刚性轮,其发生机理是车轮的20 阶谐波磨耗产生的轮轨激励频率576 Hz 触发了柔性轮对的4阶弯曲振动频率574 Hz,引发共振,使轮轨垂向力增大；轮对相同时,柔性轨下的轮轨垂向力低于刚性轨,其发生机理是柔性轨的垂向弯曲共振频率远高于车轮谐波磨耗引起的轮轨激励频率,不会引发共振,同时相较于刚性轨,柔性轨可以有效地缓解轮轨间的振动冲击,因此柔性轨下的轮轨垂向力低于刚性轨。

由图7所示的钢轨振动加速度频域图也能反映出上述规律,并从图8所示的时域图可知：刚性轨下的钢轨振动加速度呈现出近似等幅振荡的规律,其发生机理是在数值计算中刚性轨被视为移动质量轨,即将钢轨视为每个车轮下的刚性体,其计算点始终跟随于轮轨接触的下方,故会出现近似等幅振荡；而柔性轨下的钢轨振动加速度呈现出先增大后减小的趋势,其发生机理是前轮通过后钢轨振动加速度会呈现衰减状态,直到后轮通过后才完全衰减,这符合真实轮轨接触状态。

通过上述分析可以得出,4 种不同轮轨关系中柔性轮轨最符合实际情况,因此,在车轴疲劳寿命分析中采用柔性轮轨关系下的车辆—轨道耦合动力学模型。

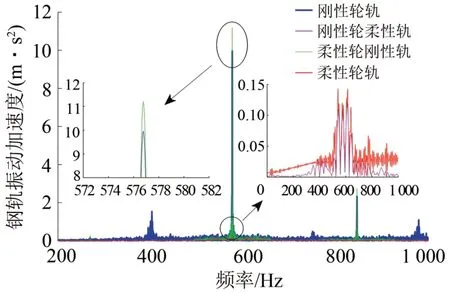
图7 不同轮轨关系下钢轨振动加速度频域图

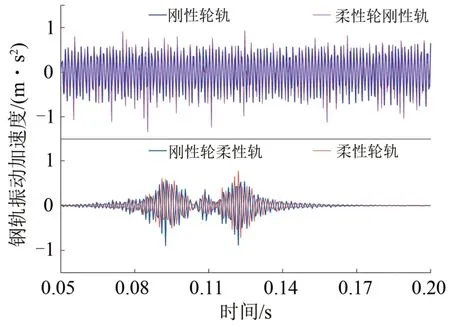
图8 不同轮轨关系下钢轨振动加速度时域图

3 车轴静强度计算

目前,国内外用于计算动车组动力车轴强度的设计标准主要有TB/T 2395—2018《机车车辆动力车轴设计方法》,EN 13104—2009《Railway applications - Wheelsets and bogies - Powered axles - Design method》和JIS E 4501—1995《Railway rolling stock-Design methods for strength of axles》。本文基于TB/T 2395—2018［13］对CRH380BL 型动车组动力车轴进行受力分析及载荷计算,其受力情况如图9所示。图中：FP1,FP2分别为施加在车轴两端轴颈上的垂向力；FY1,FY2分别为施加在轮轨接触处车轮踏面上的横向力；FQ1,FQ2分别为两车轮踏面受到的垂向反力；s为两车轮滚动圆间距的一半；l为两轴颈上垂向力作用点间距的一半；h1为轮对承载质量的重心到车轴中心线的高度；R为车轮滚动圆名义半径；Fi（i=1,2,3）为安装在两车轮之间簧下零部件质量施加的惯性力；di（i=1,2,3）为力Fi作用点至1个车轮滚动圆间的距离；FH为平衡FY1和FY2的横向力；G点为轮对承载质量的重心位置。

为方便设计和计算,标准中将各载荷简化为等效的恒幅载荷,其计算公式如下。

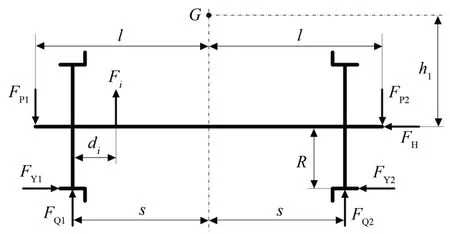
图9 车轴受力示意图

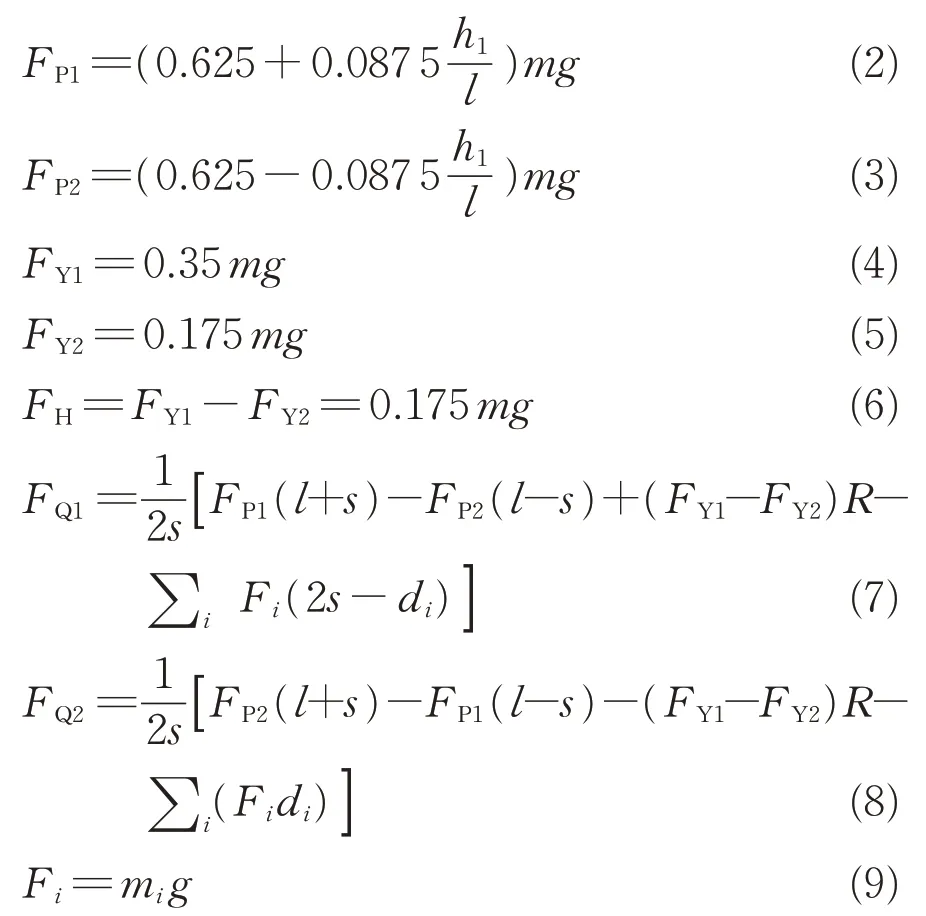
式中：m为每个轮对轴颈上的质量；mi（i=1,2,3）为簧下零部件的质量,其中m1为大齿轮的质量,m2和m3为车轴承担的驱动装置的质量。

根据CRH380BL 型动车组动车车轴的参数：m=15 370 kg,h1=1 385 mm,l=1 000 mm,s=750 mm,R=460 mm,d1=304.5 mm,d2=211 mm,d3=398 mm,m1=71 kg,m2=84.5 kg,m3=84.5 kg,Fz=11 978.2 N,g=9.8 N·kg-1。将以上参数代入式（2）—式（9）,得到分析车轴静强度所需的有限元载荷。其中,垂向载荷FP1和FP2分别为112 395.2 和75 887.3 N；横向载荷FY1和FY2分别为52 719.1 和26 359.6 N；质量载荷F1,F2和F3分别为695.8,828.1和828.1 N。

采用ANSYS 软件对轮对进行有限元离散。轮对离散化之后,在车轴2 端轴颈处施加纵向和横向节点约束,在车轮踏面上轮轨接触处的节点上施加垂向和纵向约束。在施加有限元载荷时,除了考虑运动中的质量引起的力以外,还需考虑牵引力和制动力,但由于动车主要采用再生制动,且相对于牵引工况,制动工况产生的负载更大,由于牵引工况和制动工况不会同时发生,故在分析时只考虑制动工况,即质量载荷与制动力组合。施加载荷时采用载荷步的方式进行加载,以便在FE-SAFE 软件进行寿命分析时和各载荷时间历程相关联。在车轴2端轴颈处分别施加垂向载荷FP1和FP2,在车轮踏面上轮轨接触处的节点上分别施加横向载荷FY1和FY2,在车轴齿轮箱安装座中心节点d1,d2和d3处分别施加向上的惯性力F1,F2和F3,在大齿轮的分度圆面处施加切向电制动力Fz。采用大变形非线性求解,得到5 个载荷步作用下轮对的应力结果,通过单元提取得到车轴的应力云图,分别如图10（a）—10（e）所示,并利用ANSYS软件后处理器中的Load Case 模块进行载荷组合,得到动力车轴在制动工况下的应力分布图,如图10（f）所示。

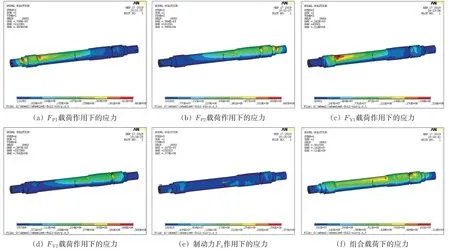
图10 制动工况下车轴的Mises应力云图

参考标准TB/T 2395—2018 和动力车轴设计图,给出车轴的主要检测部位如图11所示。基于有限元分析结果提取出上述部位的最大应力σmax,并与EA4T（25CrMo4）钢空心轴的许用应力［σ］［14］对比,得到各部位的强度安全系数η见表2。

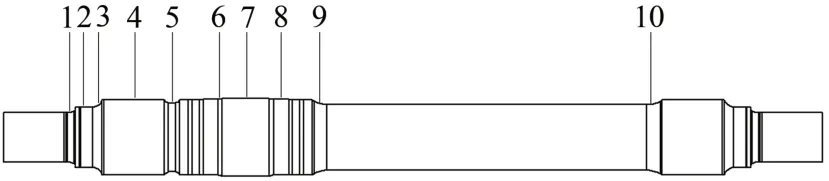
图11 车轴的主要检测部位

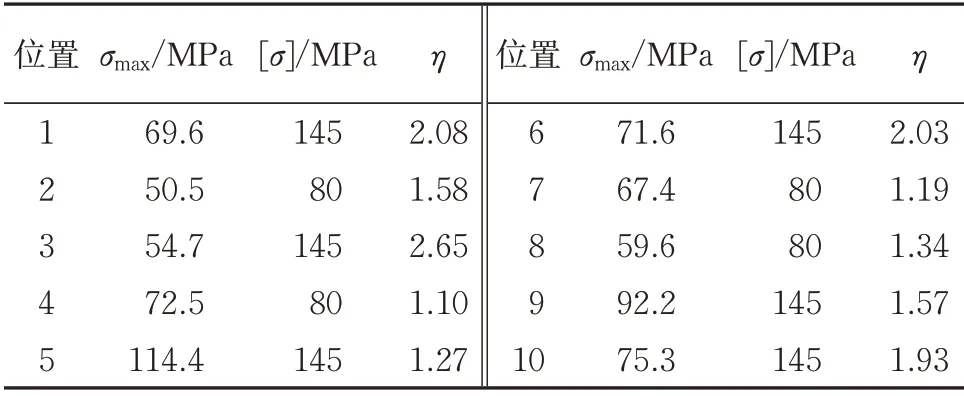
表2 各截面处的最大应力、许用应力及安全系数

结合图10和表2可知：轮座内侧圆弧过渡部位即截面5 处的应力最大,为114.4 MPa,其余各截面处的应力均较大,但各部位的最大应力均小于各区域规定的许用应力。依据TB/T 2395—2018标准中空心车轴最大应力的计算公式即式（10）计算得到截面5 处的理论应力为112.7 MPa,有限元计算结果较理论值大,其原因是有限元分析计算时考虑了轮轴过盈量的影响。相较于理论值,两者计算结果非常接近,故选取有限元计算结果进行后续疲劳寿命的仿真计算。

式中：K为疲劳应力集中系数,取1.153；MR为合成力矩,经计算为5.59×107N·mm；D1为截面5 处的直径,为180 mm；D2为空心车轴内孔直径,为30 mm。

若基于设计标准和有限元计算结果按无限寿命设计方法去评价车轴的疲劳强度,即通过多轴应力转换法计算检测部位的应力幅和平均应力,然后基于材料修正的Goodman 疲劳极限图评价车轴的疲劳强度,则认为只要检测部位的应力低于疲劳极限就对车轴的疲劳寿命没有影响。这种方法的设计载荷采用恒幅疲劳载荷,不涉及应力时间历程,也不考虑疲劳寿命的问题,按无限寿命设计。但分析过程尚未考虑各种随机激励和车轮缺陷的影响,不能确切地预估车轴的疲劳寿命。因此,在车轴疲劳寿命设计和计算中,如果按照累积损伤原则,应考虑随时间变化的动应力。故在后文中通过获取整车运行过程中的载荷时间历程,与基于标准计算出的有限元载荷相除,得到动载荷因子,然后与有限元计算的车轴上各节点的应力相乘,从而得到车轴上各节点随时间变化的应力历程。

4 考虑车轮谐波磨耗的车轴动应力计算

基于准静态法求解车轴的动应力,有2 种方法,其一：首先对每个载荷计算产生1个单位值作用下的应力,然后将其与之对应的载荷时间历程相乘,得到每个载荷的应力时间历程,然后将所有载荷的应力时间历程相加,便得到总的应力张量时间历程；其二：首先按载荷步的方式计算每个载荷作用下的应力,然后将每个载荷时间历程单位化,即载荷时间历程中载荷的瞬态值除以计算载荷,最后将单位化的载荷时间历程与有限元计算的应力相乘并叠加,便得到总的应力张量时间历程。以下基于FE-SAFE 软件采用第2 种方法求解车轴上各节点的应力时间历程。

载荷时间历程的获取方法目前主要有线路实测和动力学软件仿真2 种途径。线路实测法是通过在测试断面处贴应变片来获取某一运行区间上的应变信号,然后通过信号处理以及信号转换变为载荷信号,并经过小波处理和雨流计数法获得车轴的载荷时间历程。由于线路实测法获得的载荷时间历程只是基于某段线路下的一部分载荷,不足以具有代表车轴最大载荷发生的情况［15］。动力学软件仿真法是基于真实车辆数据建立整车动力学模型,通过数值模拟获取车辆不同运行工况下的载荷时间历程,具有成本低、速度快、精度高、高效且灵活等诸多优点。故基于动力学仿真软件来获取车轴的载荷时间历程。

考虑车轮谐波磨耗对车轴疲劳寿命的影响,基于车轮谐波磨耗的实测结果,取车轮谐波磨耗阶数为20 阶,幅值为0.02 mm,以TB/T 3352—2014不平顺谱作为轨道激励输入。根据《新建时速300～350 公里客运专线铁路设计暂行规定》（简称《暂行规定》）,建立包含直线工况以及曲线工况的线路模型。直线工况采样时长为20 s；曲线工况由直线、缓和曲线以及圆曲线构成,曲线半径结合《暂行规定》推荐值5 500～8 000 m 以及线路实际,取5 500 m,缓和曲线长度根据《暂行规定》取420 m,圆曲线最小长度根据《暂行规定》取240 m,实设超高和欠超高之和根据超高计算公式得出,为193 mm。2 种工况车速均为300 km·h-1。通过动力学仿真计算,得到2 种工况下作用在轴颈上的垂向载荷时间历程FP1（t）和FP2（t）以及作用在轮轨接触处踏面上的横向载荷时间历程FY1（t）和FY2（t）,然后将它们分别按时间历程进行组合,得到用于表征真实路线特征下的1组完整载荷时间历程如图12所示。

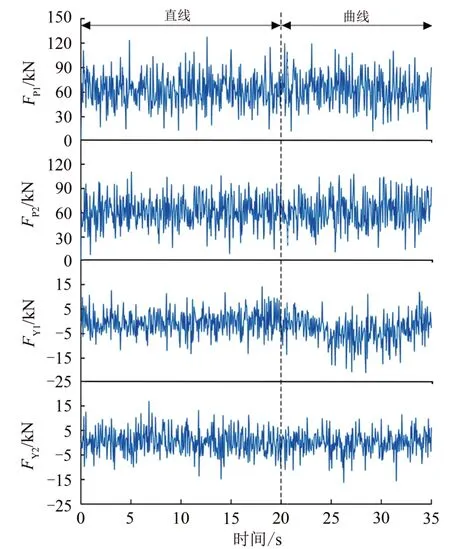
图12 谐波磨耗下的车轴载荷时间历程曲线

车轴上各节点的动应力可通过式（11）进行计算,从而得到车轴的应力时间历程。

式中：σn（t）为车轴上各节点的应力时间历程；σn为车轴上各节点的有限元计算应力；Fj（j=P1,P2,Y1,Y2）为车轴计算载荷；Fj（t）为车轮谐波磨耗下的车轴载荷时间历程。

5 车轴疲劳寿命计算

由于车轴在工作过程中处于多轴应力状态,而FE-SAFE 软件正是基于多轴疲劳分析方法进行疲劳寿命估算。因此,可以基于FE-SAFE 软件对车轴进行局部应力应变疲劳寿命分析,对于类似车轴这类延性材料的随机疲劳应采用Brown-Miller法计算,该算法认为最大疲劳损伤发生在经受最大剪应变幅的平面,且损伤与该平面上作用的剪应变和正应变有关。车轴疲劳寿命计算方法为

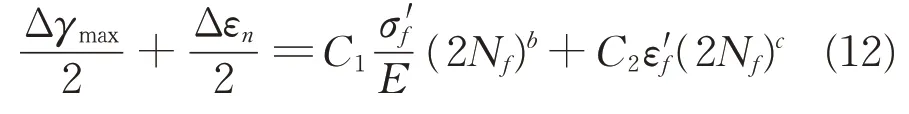
式中：Δγmax,Δεn为最大剪应变和正应变；C1,C2为常数,取1.65 和1.75；σ′f,ε′f分别为疲劳强度系数和疲劳延性系数；b,c分别为疲劳强度指数和疲劳延性指数；Nf为疲劳寿命；E为弹性模量。

计算过程主要包含有限元计算结果的提取、指定载荷历程、材料设定、分析设定等,具体如下。

（1）读入弹性计算的有限元应力；

（2）用载荷时间历程数据乘以相应的有限元应力,再除以计算载荷,得到每个张量的应力时间历程数据；

（3）根据FE-SAFE 软件提供的Seeger 材料近似算法,通过设定材料的抗拉强度、弹性模量来生成车轴材料近似的S—N曲线,其中EA4T 车轴钢的抗拉强度为783 MPa,屈服强度为561 MPa［16］；

（4）计算表面主应力的时间历程,并根据应力计算3个主应变的时间历程数据；

（5）计算每个临界平面的疲劳损伤,总损伤根据Miner 累积损伤准则叠加而成,其中最小寿命部位为裂纹发生面,并将寿命写入结果文件。

经计算,得到疲劳寿命结果文件,在ANSYS后处理模块中导入该结果文件,即可看到轮对的对数里程疲劳寿命云图,如图13（a）所示。通过单元提取,得到车轴的对数里程疲劳寿命云图,如图13（b）所示。

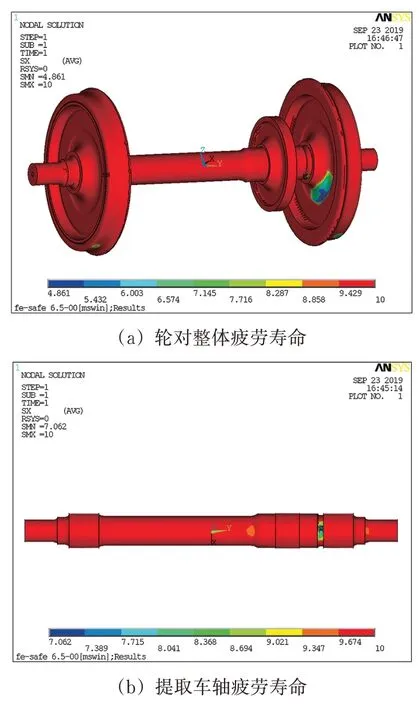
图13 车轴疲劳寿命分布图

根据图13可以看出：考虑车轮谐波磨耗下的动力车轴最小对数里程寿命为107.062km,即11 534 533 km。故车轴在运行1 153 万km 后将会发生疲劳破坏,根据该型车每年的运行里程,即按6.0×105km 计,其疲劳寿命约为19.2 a。发生在轮座内侧圆弧过渡部位,进一步分析得知除轮座内侧圆弧过渡处,防尘板座和齿轮座左侧圆弧过渡处的寿命也较短。显然同文献［7］不考虑车轮谐波磨耗时计算出的车轴疲劳寿命28.6 a相比存在较大差别,表明车轮谐波磨耗对车轴疲劳寿命具有显著影响。考虑车轮谐波磨耗后,车轴的疲劳寿命小于《铁路动车组运用维修规程》中设计寿命20 a 的规定。其原因主要是车轮谐波磨耗激发了轮对的4阶弯曲振动模态,产生共振,使轮轨间的动作用力增大,在大应变的作用下导致车轴轮座内侧圆弧过渡处发生疲劳破坏。由于该寿命为基于车轮旋修前的高阶车轮谐波磨耗下的疲劳寿命,属于极端不利因素下的疲劳寿命,因此,不能表明该车轴不满足设计要求,因为运营维护单位不会让高阶车轮谐波磨耗一直存留于车轮上,但需对高阶车轮谐波磨耗引起足够重视,如不及时对其进行镟修处理,便会严重影响车轴的疲劳寿命。虽然对比文献［7］研究的是CRH380B 型动车组车轴,但两者的计算载荷相差很小,在5%以内,加之2 个车轴的材料和加工制造工艺完全一致,故可选用CRH380B 型动车组车轴疲劳寿命作为寿命对比参考对象。同时,若轮座内侧圆弧过渡处,防尘板座和齿轮座左侧圆弧过渡处存在诸如微观裂纹、锈蚀等缺陷,将极易造成早期疲劳破坏,因此,在进行轮轴检修时,如发现车轮谐波磨耗等车轮多边形现象,应予以重点关注,对高阶谐波磨耗应及时进行镟修处理。

6 结 论

（1）基于TB/T 2395—2018 中的材料力学法和有限元方法分别计算得到车轴的最大静应力为112.7 和114.4 MPa,均位于轮座内侧圆弧过渡部位即截面5 处,其余各截面处的应力均较大,但各部位的最大应力均小于各区域规定的许用应力。2 种方法计算所得最大静应力的差值在1.5%,由于有限元分析中考虑了轮轴过盈量,故有限元计算应力大于理论计算值。

（2）通过动力学分析得到了考虑车轮谐波磨耗下的载荷时间历程,并与轮对有限元分析结果相关联,通过准静态法获得车轴动应力。针对车轴延性材料,确定采用Brown-Miller组合剪切应变与法向应变法作为寿命计算方法,计算得到考虑车轮谐波磨耗因素的车轴疲劳寿命为19.2 a,发生在轮座内侧圆弧过渡部位。该部位既是有限元静强度分析时应力最大的部位,也与段修时车轴常出现横裂纹的统计部位相吻合。考虑车轮谐波磨耗后,车轴的疲劳寿命小于《铁路动车组运用维修规程》中设计寿命20 a的规定。由于该寿命属于极端不利因素下的疲劳寿命,因此,不能表明该车轴不满足设计要求,但需高度重视高阶车轮谐波磨耗的严重影响,并及时对其进行镟修处理。研究成果为车轴运用维修提供了参考依据。