联络通道冻结施工近隧道端土体温度场分布及管片保温措施优化
2020-06-10岳祖润张基伟孙铁成
张 松,岳祖润,张基伟,孙铁成,王 磊
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄 050043;3.北京中煤矿山工程有限公司 冻结与轨道交通工程公司,北京 100013;4.石家庄铁道大学 研究生学院,河北 石家庄 050043;5.煤炭科学研究总院 建井研究分院,北京 100013)
隧道联络通道人工冻结法施工中最易出现的风险是土体与管片接触区域(下文简称交界面区域)的冻结壁强度不足,交圈不理想导致的开挖时涌水、冒砂。工程中该区域受隧道通风换热[1-2]、管片焊接作业等因素影响,交圈时间最慢、降温效果最不理想。在作者参与的上海地铁某联络通道工程中由于交界面区域冻结壁温度降低缓慢,难以在规定时间满足冻结设计要求,被迫延长冻结工期15 d,耗电量增加约4.5 万kW·h,人工费用增加约3.6万元,总成本增加约5%。
近年来,人工冻结法在城市地铁工程中得到了广泛的应用,在地铁隧道[3-4]、区间联络通道[5-6]、盾构端头井[7]等地下工程中均有冻结法应用的案例。长三角地区95%以上的地铁联络通道采用冻结法进行施工。
人工冻结法的核心是对地层温度场的控制[8],温度场决定了土体的承载、封水能力,对此学者们开展了大量的研究。胡向东[9-10]基于单排管稳态温度场的巴尔霍金解进行推导,提出了不同冻结管布置形式的温度场解析解,对于温度场进行了可靠的预测。王志良[11]采用变量代换方式求解了单管冻结箱变热传导控制方程,得到了温度场表达式的解析解。耿萍[12]采用数值模拟计算的方法对于冻结法的水、热、力耦合问题进行了研究,提出了应根据实际施工需要调整冻结参数,减少冻结时间,防止冻结壁的过度扩展。此外,Yan Qixiang[13]、黄诗冰[14]、杨平[15]等学者也通过模型试验、数值计算等方法对冻结温度场开展了一系列的研究。但这些研究集中于受隧道散热影响较小的深部温度场,对于交界面温度场关注较少。
胡向东[16]采用现场实测的方法进行研究,认为管片附近“喇叭口”位置受外侧散热影响严重,其影响区域冻结壁最小厚度仅为未受影响区域的一半,且积极冻结后期由于热交换达到平衡状态,该区域冻结效果增加并不明显;张松[17]针对交界面区域散热严重问题,对于管片隧道侧冷冻排管设置进行研究,优化了冷冻排管的形式和布置间距。但上述研究并未能给出交界面段温度场的整体演化规律和冻结不足的解决办法。
综上所述,目前对交界面区域的研究仍有不足,无法精准有效地确定交界面段的冻结效果。该区域是冻结工程的最薄弱区域之一,如果无法精准有效地评估其冻结效果,将会对工程安全产生较大的威胁。因此,本文基于上海地铁某联络通道现场测温数据和有限元模拟数据,分析交界面区域温度场的分布,研究交界面区域冻结壁的形式和发展规律,提出管片保温措施优化建议。
1 温度场控制方程和土体参数
不考虑土体内可能存在的渗流等因素,将土体温度场求解视作瞬态问题,则土体温度场的控制方程为[18]

式中:T为土体温度,℃;t为时间,s;Ceq为土体的等效比热容,J·(kg·℃)-1;keq为土体的等效导热系数,W·(m·℃)-1,由冰、水、土颗粒三者含量与热物理参数共同决定;Li为水冰相变潜热,J·kg-1;ρw为水的密度,kg·m-3;Δωi为土体内含冰量的增加量,该值随温度变化发生改变,m3;QG为其他热源汇总项,J。
QG在土体内取0,在交界面取值为

式中:ks为管片与隧道空气间的传热系数,W·(m2·℃)-1,综合考虑管片附近热辐射、热传导、热对流得出;Ta为管片周围空气温度,℃;Ts为管片表层温度,℃;A为热交换区域面积,m2。
土体热物理参数参考类似工程[19]及相关工程地勘资料获取,数据见表1。为了避免有限元计算中数值突变引起的收敛困难,在冻结温度(根据采样重塑土冻结温度试验取-0.23 ℃)附近区间采用海维赛德阶跃函数H(T)进行平滑过渡,函数形式绘于图1。以导热系数为例,计算中等效导热系数keq计算公式为
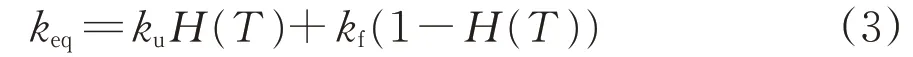
式中:ku和kf分别为未冻土、冻土的导热系数,W·(m·℃)-1。
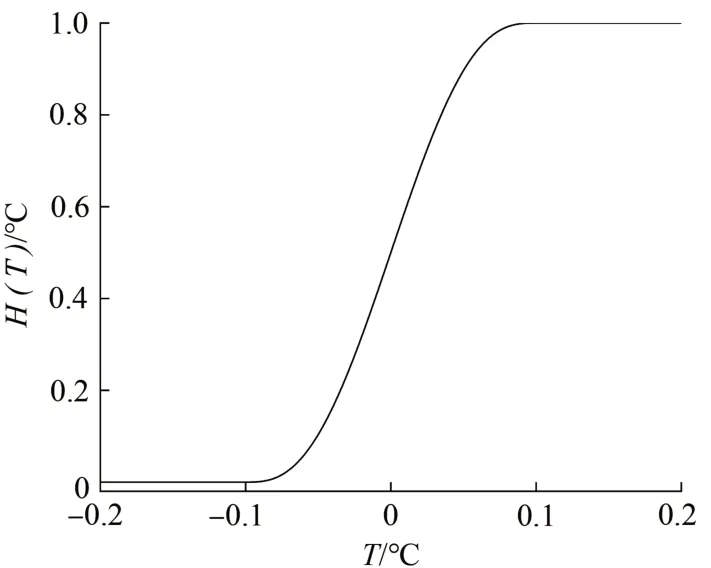
图1 H(T)函数曲线
2 模型的建立与验证
2.1 有限元模型
以上海地铁某联络通道工程为例,根据冻结现场工况,建立6 m×6 m×10 m 长方形三维有限元联络通道模型,在土体中部设置上下排列的3根冻结管,冻结管的长度为6 m,外半径为89 mm,冻结管的间距为变量d,根据模拟工况改变其取值。设置土体四周0.5 m 为无限元域,模拟土体四周工况;靠近管片一侧350 mm 区域设为钢筋混凝土管片;管片外侧设为薄层结构,模拟50 mm 厚聚苯乙烯保温层。采用四面体网格进行网格划分,模型形式及网格划分如图2所示。
2.2 边界条件
根据现场实测结果,选择土体初始地温为16.32 ℃,管片外侧空气温度为16 ℃,冻结管外壁温度按现场实测温度设置,其余区域设置为热绝缘状态。盐水温度变化曲线如图3所示
2.3 模型验证

图2 有限元模型及网格划分

图3 盐水温度变化曲线
选取冻结界面上距离冻结管0.9 m 处测温孔C3 的实测温度,对模型进行验证。取d=0.6 m,采用上文计算模型计算该处的温度,并将计算值与实测值的差值作为偏差值,均绘于图4。

图4 测温孔位置计算值与实测值
由图4可知:计算值与实测值变化趋势一致;最大偏差值为1.86 ℃,出现在冻结第6 d。偏差的原因主要在于:实际工程中测点位置测量精度不足;有限元计算中水冰相变潜热按原有水分全部转换为冰体计算,并未考虑冻结过程的水分迁移;以及地勘数据揭示的土体含水率精度不足。综上所述,该计算模型可有效模拟积极冻结40 d期间土体温度场的变化,因此该模型是可靠有效的。
3 交界面温度场
在案例施工过程中,由于土体交界面位置降温缓慢,因此积极冻结40 d时,在冻结界面距离冻结管0.8 m 位置施工探孔,探孔深度1.0 m,孔内每间隔0.2 m 布置1 个测点,实测交界面温度场。同时采用上文计算模型计算该处的温度:冻结管间距取d=0.6 m;由于实际施工中夏季隧道潮湿水蒸气冷凝后大量附着于保温板上,保温板孔隙在工程初期已基本充满水分,根据以往研究表明,保温材料遇水后将大幅增加导热系数[20],且后期因隧道预应力支架安装,部分保温板被拆除,因此计算中忽略保温层;为了研究探孔深度未涉及区域的温度场,继续模拟计算1.0~3.0 m 深度(与探孔深度统称为深度)区域的土体温度;将实测值与计算值绘于图5。由图可知:交界面区域土体温度随深度增加迅速下降,实测与数值计算温度的下降趋势基本一致,最大偏差为1.0 ℃。该结果进一步验证了交界面区域温度场计算结果的有效性。
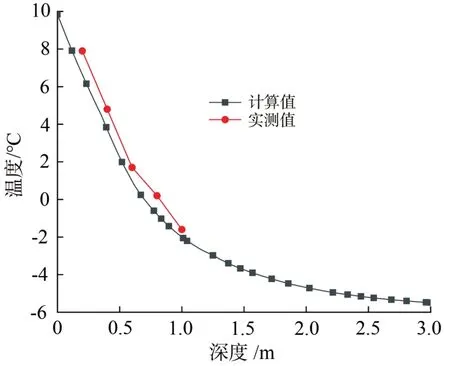
图5 探孔位置计算值和实测值
对计算的交界面温度T与深度h进行数据拟合,得到两者的拟合关系式为

由式(4)可知:探孔温度随深度的增大呈指数型下降;深度较小时,随着h的增大,土体温度迅速下降;深度较大时,随着h的增大,温度变化逐步趋缓,土体温度更加稳定。
根据有限元计算结果绘制冻结管界面等温线如图6所示。图中:下端为管片外表面位置,横向坐标为与冻结管中心距离,竖向坐标为距离管片外表面深度,洋红色0 ℃等温线表示冻结锋面位置。由图6可知:冻结壁厚度呈纺锤形,冻结壁厚度随深度的增加先迅速增长,随后逐步趋于平缓。冻结壁扩展厚度Wf(h)与深度h的数据拟合公式如式5 所示,可见冻结壁扩展厚度也随深度的降低呈指数型降低。将式(5)对深度h求导,可得冻结壁厚度变化率Wf′(h)如式(6)所示。根据式(6)计算可知,当h>2.2 m 时,Wf′(h)<0.1,此时冻结壁厚度变化基本可以忽略不计。
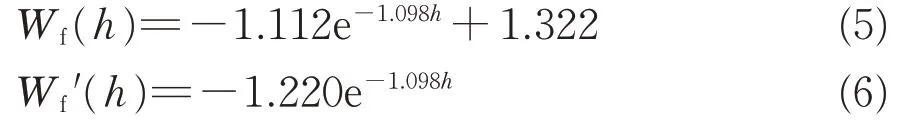

图6 管片后界面等温图(单位:℃)
对比分析实测值和计算值可知,温度场分布及冻结壁厚度在靠近管片区域和距离管片较远区域有明显差异。据此可将联络通道的冻结区域划分为:受管片散热影响显著的两侧交界面段和管片散热影响可以忽略的正常冻结段。在本案例中的交界面段与正常冻结段的划分位置可为h=2.2 m 位置,根据计算可以看出在h<1.0 m 范围土体受管片散热影响最为严重,该区域内冻结壁强度弱、厚度薄,对冻结施工的安全有极大的负面影响。
4 冻结管间距与保温效果对冻结壁厚度的影响
4.1 冻结管间距对冻结壁厚度影响
取冻结管间距d=0.6,0.8,1.0,1.2 m,积极冻结40 d,计算不同深度时的冻结壁厚度,结果如图7所示。由图可知:对于深度大于1.0 m 区域,冻结管间距对冻结壁厚度影响约占冻结壁总厚度的5.9%,影响基本可以忽略;而在深度小于0.5 m 区域,对冻结壁厚度影响约占冻结壁总厚度的26.4%,因此在交界面段的靠近管片一侧,冻结管间距是冻结壁厚度的决定因素之一。
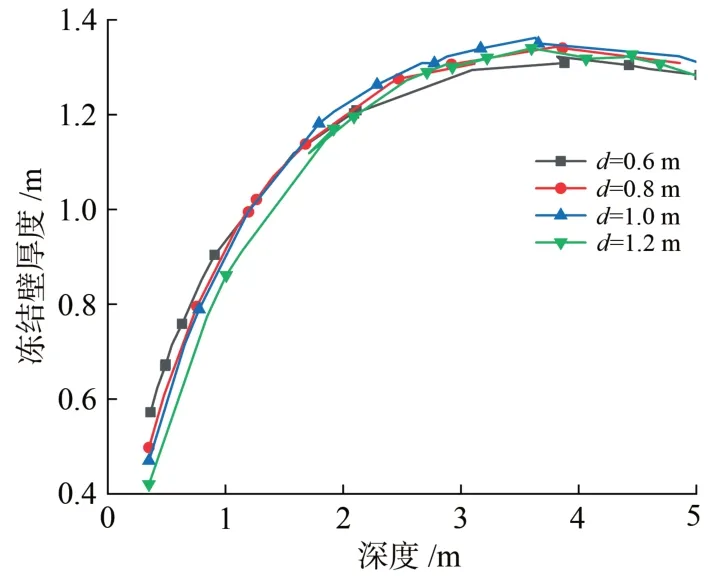
图7 不同冻结管间距时冻结壁厚度与深度的关系曲线
在实际案例中,冻结管主冻结面(主要钻孔及开挖隧道工作面)的开孔位置间距为0.6 m 左右,在辅助冻结面(少量短孔钻孔隧道工作面)的终孔位置间距约为1.0~1.2 m。因此,在条件相同情况下,辅助冻结面的冻结壁厚度要小于主冻结面约0.3 m(冻结管2侧厚度相加),成为冻结壁的最薄弱点。根据多个工程的实测数据显示,辅助冻结面冻结管在安装冷冻排管情况下仍远小于主冻结面冻结壁厚度。为保证冻结工程安全,建议根据测温数据,在辅助冻结面设置补充冻结孔,以增大冻结壁厚度。
4.2 保温效果对冻结壁厚度的影响
实际工程中,若保温材料受水分侵蚀以及隧道预应力支架安装破坏,往往导致保温效果削弱、甚至失效的情况,而根据上文结论可知,交界面段冻结效果薄弱。因此,采用上文模型,分别计算有效保温和无效保温2 种情况下交界面段冻结壁的厚度,结果如图8所示。由图可知:在交界面段,两者冻结壁厚度差约为0.5~0.6 m;在正常冻结段,两者冻结壁厚度差约为0.05~0.10 m,此值较小可以忽略。在交界面段,冻结壁厚度与深度关系呈对数型增长,但幅度变小。由此可知,采用有效保温措施,可提升交界面段内的冻结壁厚度,但无法彻底避免管片散热对于冻结壁温度场的影响。
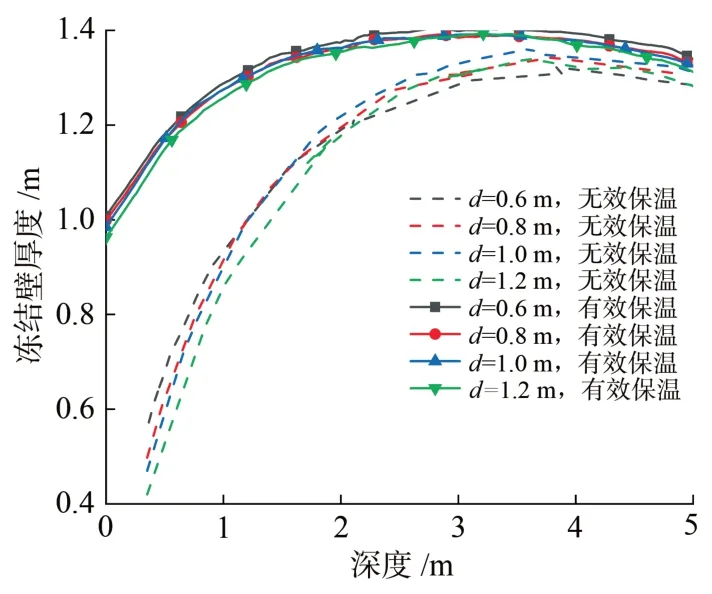
图8 有无有效保温时冻结壁厚度与深度的关系曲线
除保温失效问题外,冻结后期因作业需要去除部分保温,随后又未及时恢复,也是目前工程中存在的常见问题,为了研究这一工况,冻结管间距d=0.6 m,计算积极冻结30 d、随后去除保温板10 d共计40 d的冻结效果,并将其与积极冻结40 d有效保温、无效保温的冻结效果对比,结果如图9所示。由图可知:在深度0.35~2.40 m范围内,冻结壁厚度明显减少,与上文计算所得影响范围基本一致;冻结壁厚度介于持续不保温与持续保温之间。
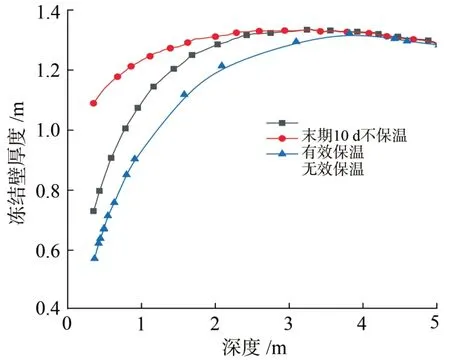
图9 不同保温状态时冻结壁厚度与深度的关系曲线
综上所述,保温材料可以有效降低管片散热效果,因此施工中需避免保温材料破损以及水分侵蚀所导致的导热系数增加、保温失效等问题。
4.3 管片散热对温度场的影响
为了标定管片散热的影响范围及效果,参考文献[16]建立管片散热影响系数计算公式为

式中:ξ(h,t)为交接面段指定冻结时间与位置的冻结壁厚度,m;ξmax(t)指定冻结时间时正常段的最大冻结壁厚度,m。
积极冻结40 d时散热影响系数与深度的关系曲线如图10所示,可见,当h>2.2 m 时,散热影响系数不足0.01,因此管片散热对该区域的影响可以忽略。

图10 散热影响系数与深度的关系曲线
为了研究不同冻结时间散热影响系数的分布,取d=0.6 m,冻结时间t=10,20,30,40 d,计算结果如图12所示,以散热影响系数η=0.05为划分管片散热影响效果的标准,当η≥0.05时,认为管片散热对该区域有影响。由图11可知:随着冻结时间的延长,管片散热影响范围会逐步增大。对积极冻结时间和影响范围进行回归分析,可得公式(8),其中s为管片散热对温度场的影响范围。公式表明,随着冻结时间的延长,管片散热对土体温度场的影响呈对数型增大。

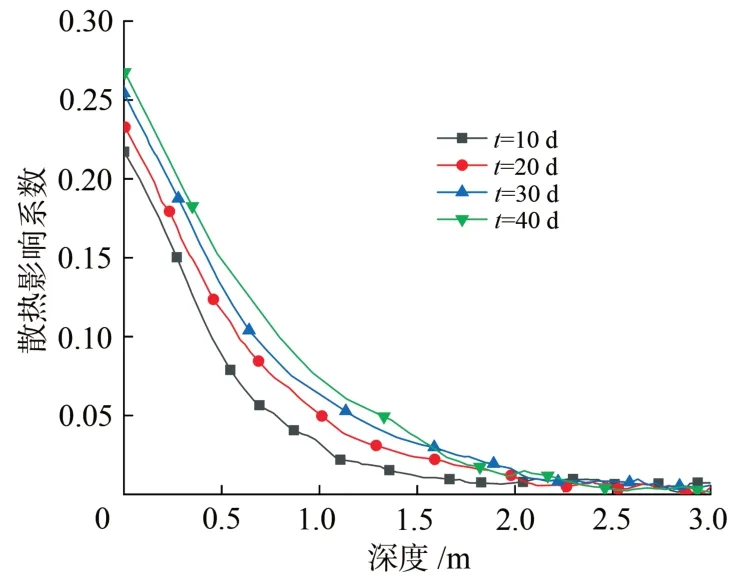
图11 不同冻结时间的散热影响系数与深度的关系曲线
5 管片保温措施优化
综上所述,对管片采用保温覆盖的方法,可较为有效地解决管片散热对土体冻结效果的影响,但目前常规的保温方案容易受隧道环境和人为因素影响,出现损伤或破坏,难以满足施工需要。为了保证管片保温效果,提出如下2 个管片保温措施优化方案。
方案1:对钢管片的结构形式进行优化,在钢管片内部靠近土体一侧增设5 cm 夹心保温层,实现保温层内置,避免了外部施工可能产生的保温层损毁,并实现了全断面的有效保温,设置形式如图12所示。
方案2:将常规的保温板覆盖方法替换为在管片与土体接触区域进行改良注浆的方案,通过浆液材料降低该区域土体的导热系数,形成类保温层土体,实现管片的内保温。浆液改良:浆液掺入陶粒或EPS 颗粒,制备密度更高、隔热效果更好的浆液。施工时机:管片拼装完成后进行注浆。

图12 钢管片结构形式优化
上述2 个方案成型后效果基本一致,即在管片内部形成一道无法破坏且隔热效果良好的隔温层,将保温层效果等效5 cm 聚乙烯保温板,利用上文有限元模型计算并与无优化模型对比,将冻结管轴面温度场对比绘于图13,可以看出,在优化设计后,在靠近管片位置冻结壁厚度增加了约24%,增加效果明显。

图13 轴面温度场优化前后对比
6 结 论
(1)土体温度、冻结壁扩展厚度均随深度的增加呈指数型变化。即随着深度的增加,土体温度迅速下降,冻结壁扩展迅速增加,随后均趋于平缓;当深度大于2.2 m 时,冻结壁厚度和温度场的变化基本可以忽略不计。
(2)联络通道冻结加固区域划分为:受管片散热影响的两侧交界面段和不受管片散热影响的正常冻结段。
(3)冻结管间距是影响交界面段冻结壁厚度的重要因素之一,受其影响辅助冻结面冻结壁厚度明显小于主冻结面。为保证安全,建议通过辅助冻结面补充冻结孔进行冻结壁优化。
(4)管片散热对土体的影响范围与冻结时间呈对数关系,随着冻结时间的延长,影响范围逐步增大,但增速逐步放缓。
(5)为了保证交界面区域的冻结效果,提出在钢管片内部靠近土体一侧增设5 cm 夹心保温层或改良管片壁后注浆材料2 种管片保温优化措施,优化后,交界面段靠近管片位置冻结壁厚度增加了约24%。
