浸水作用下重载铁路基床动回弹模量衰减规律
2020-06-10冯怀平宋慧来常建梅魏亚辉
冯怀平,宋慧来,常建梅,魏亚辉
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.中国国家铁路集团有限公司 工程管理中心,北京 100844)
货运重载化是我国交通运输发展的重要方向之一,其中重载铁路运输因其运输能力强、效率高、经济效益好等优点而受到广泛关注[1]。重载铁路基床作为承受基床上部荷载的关键结构[2-3],对保证重载列车的安全运营起着至关重要的作用。与普通铁路基床和公路基床不同,重载铁路基床会承受由于重载列车的持续大轴重运输引发的对于基床的高动应力循环加载,再加之由于降雨导致的雨水浸入基床[4-5],使得重载铁路基床同时承受高动应力循环加载和湿化耦合的动力湿化作用[6],极易造成基床土体局部刚度软化,并随着列车运行对软化部位的持续冲击,使得软化范围进一步扩展,从而严重影响轨道平顺性,威胁行车安全。动回弹模量作为评价基床土体性能的关键参数[7],是土体刚度的直观表征,因此研究动力湿化作用下基床土体动回弹模量的衰减规律有助于防止轨道不平顺现象的产生,保障列车安全运营。
动回弹模量的概念最早由Seed 等[8]在1962年提出,其定义为土体所受的动应力幅值与弹性应变之比。随后大量的研究表明[9-14],循环荷载作用下土体的动回弹模量具有强烈的应力依赖性,动回弹模量随着动应力幅值的增大而增大,因此有必要针对重载铁路基床在高动应力循环加载作用下的动回弹模量演化规律进行研究。而关于土体初始状态对动回弹模量的影响,Mehrotra[15]等和Salour[16]等研究发现土体的动回弹模量随着土体水分含量的变化而变化,具有强烈的湿度依赖性;Gabr 等[17]和Liang 等[18]则认为土体的回弹能力很大程度上与其自身密实程度紧密相关,因此有必要考虑不同初始含水率、压实程度对土体动回弹模量的影响。
此外,在关于土体软化模型的构建上,Idriss等[19]提出了软化指数的概念,并建立软化指数与加载次数的表达式;蔡袁强等[20]则在Idriss 软化指数的基础上,以动弹性模量重新定义软化指数,建立应变软化经验模型。然而在动力湿化作用下,土体会持续产生较大的累积塑性变形[21],此时的滞回曲线难以闭合,选用动回弹模量反映土体刚度更为合适。图1为未浸水土体、浸水后土体在经历一段时间的循环加载作用后的滞回曲线。由图1可以看出:没有浸水作用的土体在经历一段时间的循环加载后,其滞回曲线近似闭合,此时滞回曲线的2 个顶点连线的斜率k既可以代表动弹性模量,也可以代表动回弹模量(如图1(a));但是经受动力湿化作用的土体,在每次加载后都会产生较大的塑性应变εp,导致滞回曲线无法闭合,其滞回曲线的顶点连线有2 条(如图1(b)),2 个斜率k分别表征动弹性模量和动回弹模量,此时动回弹模量更能代表土体的回弹特性,反映土体刚度。因此,本文参照蔡袁强等人[20]的定义方法,以动回弹模量代替动弹性模量构建动力湿化作用下的软化指数,并建立动力湿化作用下的土体刚度软化模型,以描述土体的抗变形能力衰减。
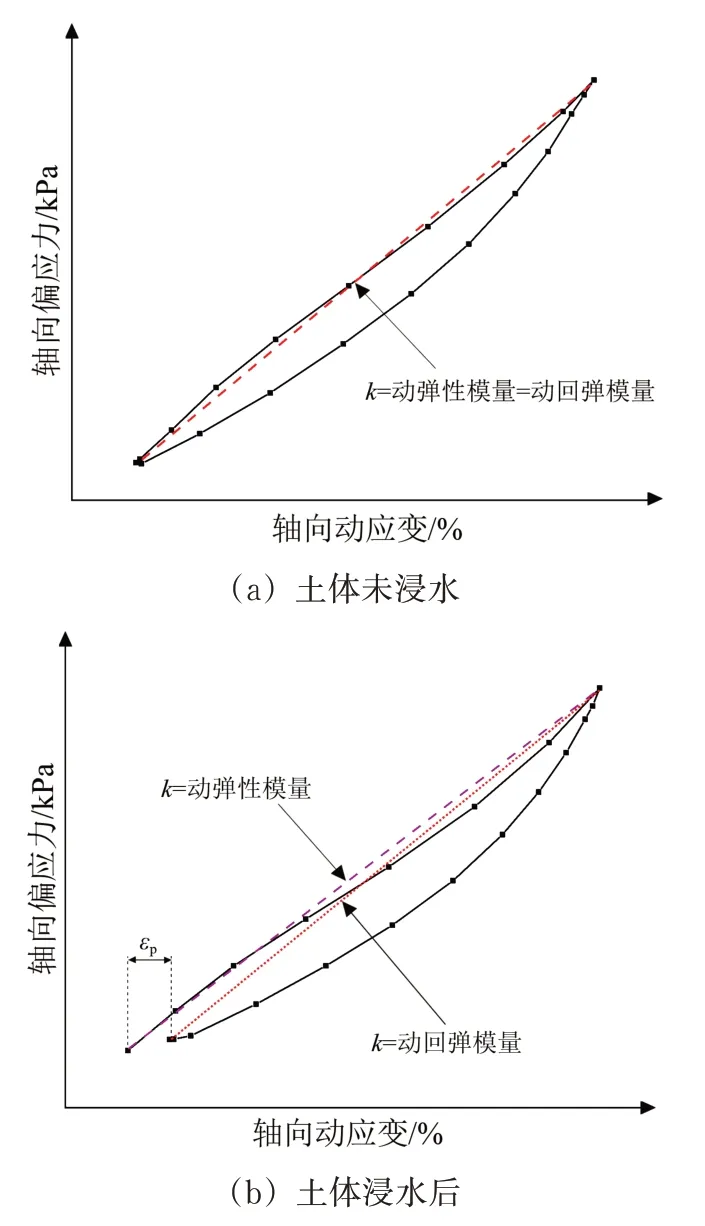
图1 浸水、未浸水土体滞回曲线对比
在运营的既有线路中,由于早期设计对线路运量及轴重预估不足,考虑降低设计和施工成本,粉土及粉质黏土常被用于基床填料,近年来随着经济的快速增长,既有线路不断扩能升级,引发大量基床病害[22-24]。本文试验中土体取自包神铁路某病害段,土质为粉质黏土。利用GDS动三轴系统模拟实际加载环境,使用自行研制的常水头马氏瓶模拟雨水自然浸入基床,构建动力湿化环境,考虑土体的初始状态(不同压实系数、不同含水率条件)研究基床土体在动力湿化作用下的动回弹模量衰减规律。
1 动三轴试验
1.1 动三轴试验系统
本试验采用英国GDS公司生产的DYNTTS动静三轴系统,如图2所示。其中浸水装置引入改进的常水头马氏瓶,如图3所示。常水头马氏瓶通过侧壁开口处与大气连通,使得侧壁开口高度为其自身水头高度,实现瓶内液体下降时马氏瓶水头恒定的目的。由于室内温度与气压在长期加载试验中很难保持恒定,因此传统马氏瓶在使用过程中不可避免地出现漏水与吸气现象,极大影响了测试精度,而改进马氏瓶在通气孔处设置储水调节杯,可以有效降低这一误差。将三轴仪底座中的备用排气孔与马氏瓶相连即可实现实时补水。

图2 GDS动三轴试验系统
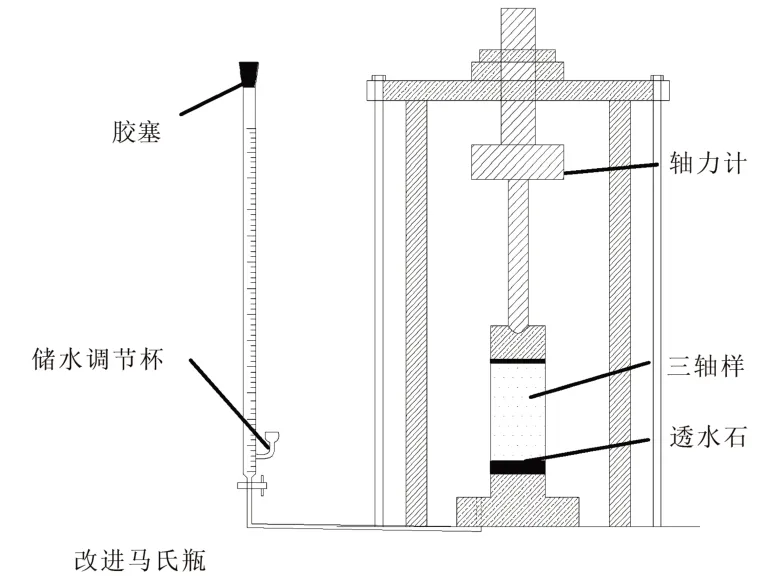
图3 浸水装置示意图
1.2 试验土样
试验土样取自包神铁路瓷窑湾站,其基本物理参数见表1。依据TB 10102—2010《铁路工程土工试验规程》[25]和SL 237—1999 《土工试验规程》[26]制备出压实系数K分别为0.9,0.93 和0.96,含水率w分别为8%,10%和12%的动三轴试样。试样直径为61.8 mm,高度为125 mm。

表1 试样物理参数
1.3 加载方案
本试验在加载过程中,以半正弦波进行加载。取土地区长期开行C80型货物列车,其车辆全长为12 m,列车平均运营速度为73.85 km·h-1[27],列车运行时基床土体所承受的加载频率f=v/l(v为列车运行速度;l为车辆全长)约为1.71 Hz,故选取2 Hz 作为本文试验加载频率。根据苗雷强[28]的现场实测结果,C80型货物列车的动应力幅值在90~100 kPa 之间,围压在25 ~60 kPa 之间,但考虑铁路扩能改造会使得列车轴重增加,因此试验中设定动应力幅值为120 kPa、围压为30 kPa,并考虑基床上部静荷载(即加载时的接触荷载),设定静偏应力为20 kPa。为模拟雨水入渗基床,马氏瓶侧壁开口高度保持在三轴仪底座排气孔上方高度5 cm的位置不变,以保证浸水过程的恒定水头差。
为模拟重载铁路实际运营期间,已因列车运行而达到动力稳定的基床土体,同时承受列车循环加载和浸水作用耦合的动力湿化作用的实际工况,设置以下3个试验阶段。
(1)固结阶段。考虑基床上部静荷载,对土样进行偏压固结,使其达到固结稳定状态。
(2)动力稳定阶段。对已经达到固结稳定的土体进行循环加载,加载时试验不排水,并使其在循环加载作用下达到动力稳定状态。经过多次试验发现,循环加载次数接近1 000 次时土样皆可达到动力稳定状态,故设定1 000 次为动力稳定阶段的循环加载次数。
(3)动力湿化阶段。当土样已经处于动力稳定状态后,继续进行循环加载并打开进水阀门,土样进入动力湿化阶段。当土样应变达到10%或循环加载次数达到50 000次时,关闭进水阀门,停止试验。
图4为上述3 个试验阶段的全程轴向加载示意图。图中:σ3为围压;σ0为轴向静偏应力;σd为加载波形波峰和波谷的差值,即循环加载时的动应力幅值。因此轴向应力在波谷处为(σ3+σ0),波峰处为(σ3+σ0+σd)。
2 动力稳定阶段试验结果及分析
滞回曲线的平移距离可以在一定程度上表征土体塑性应变的累积程度。
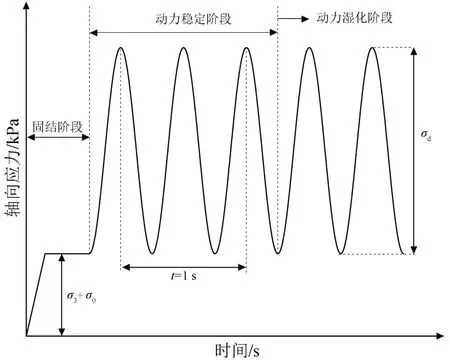
图4 轴向荷载加载方式
图5给出了动力稳定阶段不同含水率、不同压实系数土体的滞回曲线。图中:εp,100为前100 次循环加载所累积的塑性应变;εp,1000为前1 000 次循环加载所累积的塑性应变(即动力稳定阶段的总塑性应变);N为循环次数。
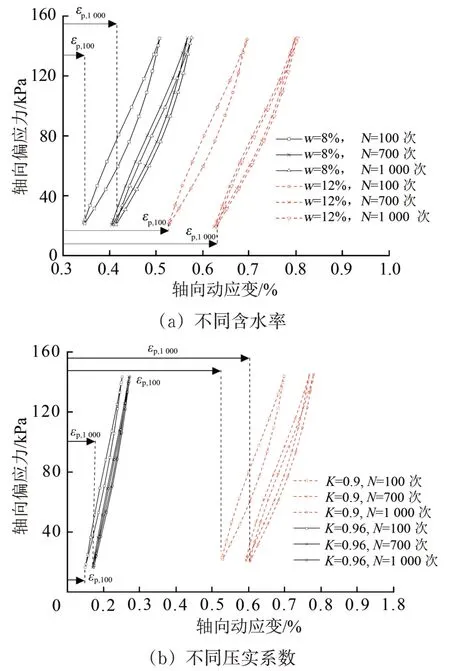
图5 不同含水率、压实系数条件下的滞回曲线
由图5可以看出:在动力稳定阶段,不同含水率、不同压实系数土体的滞回曲线的平移距离不同,前100次循环加载的累积塑性应变占动力稳定阶段总塑性应变的84%以上,700 次循环加载之后产生的累积塑性应变不超过此阶段总塑性应变的2%,表明土样在加载前期会有较大的塑性应变累积,之后随着循环加载作用的进行逐渐进入动力稳定阶段,而压实系数越大、含水率越低的土体滞回曲线平移距离越小,即累积塑性应变越小。
动回弹模量由土体外界的应力状况与自身的弹性变形(即回弹变形)共同决定,其计算式为

式中:Er为动回弹模量;εr为弹性应变。
图6给出的动回弹模量计算所用物理量的确定方法。根据图6中的计算方法,绘制出不同含水率和不同压实系数的动回弹模量与循环加载次数的关系曲线,如图7所示。由图7可以看出:在动力稳定阶段,动回弹模量在前100 次循环加载内增长较快,随后逐渐趋于稳定,这与其滞回曲线的平移规律相吻合。而压实系数越大、含水率越低的土样,当其进入动力稳定状态后的动回弹模量越大。

图6 动回弹模量计算示意图
3 动力湿化阶段试验结果及分析
3.1 浸水量
在动力湿化阶段,不同压实系数土体的浸水量存在差异。图8给出了相同初始含水率土体在压实系数不同时的浸水量随浸水时间的变化曲线。曲线每一点的切线斜率可表征浸水速率。由图8可以看出:在动力湿化前期浸水速率较大,随着浸水过程的持续进行,浸水速率逐渐减小。在整个动力湿化过程的浸水量相当于含水量增加3.8 %~4.9 %,试样底部饱和;初始压实系数越大,浸水量越小,土体抵抗动力湿化作用的能力越强。
3.2 累积塑性变形
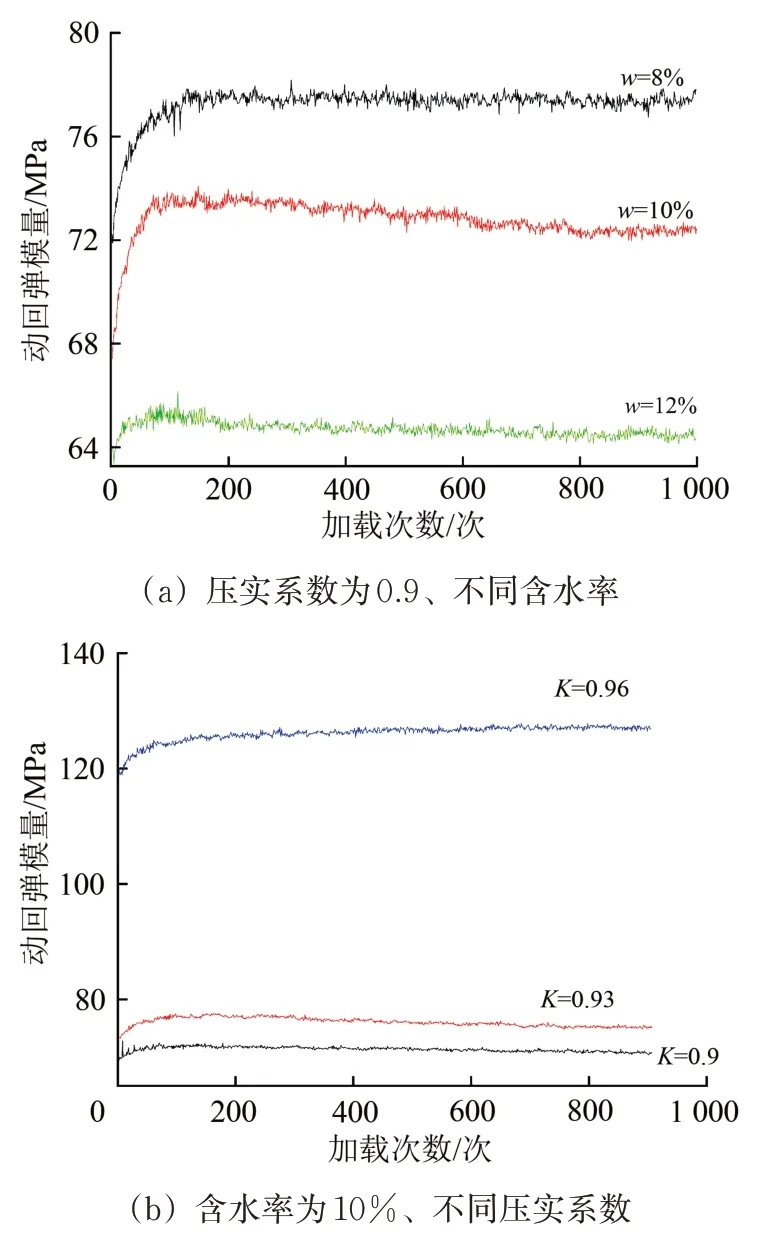
图7 动回弹模量—加载次数曲线
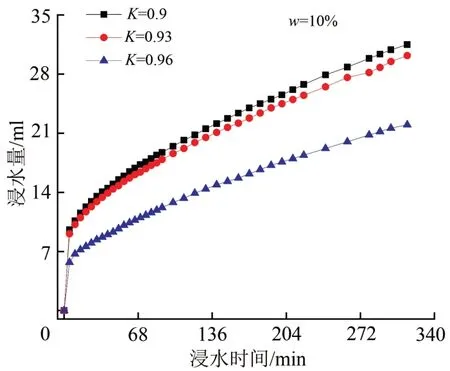
图8 浸水量—浸水时间关系曲线
当进入动力湿化阶段后,浸水过程会立即打破土体原有的动力稳定状态,并产生明显的塑性变形。图9为动力湿化阶段不同含水率和不同压实系数土体的累积塑性应变随加载振次的变化曲线。由图9可以看出:当初始含水率相同时,不同的初始压实系数会导致土体动力湿化阶段的累积塑性变形明显不同;当初始压实系数相同时,不同初始含水率土体的累积塑性变形相近;压实系数为0.9 和0.93 的土体在循环加载次数分别为35 000 次和46 000 次时,已达到10%的累积塑性应变;压实系数为0.96 的土体在循环加载次数达到50 000 次时,累积塑性应变仍不足3%。可见,压实系数是影响土体动力湿化阶段抗变形能力的关键因素。
3.3 动回弹模量的软化

图9 累积塑性应变—加载次数曲线
在动力湿化阶段,滞回环除了发生平移之外,滞回环2 个顶点连线的斜率也在逐渐发生变化。为直观研究滞回曲线的倾斜程度变化,将不同振次下的滞回曲线平移至原点进行对比分析。图10为压实系数为0.96,含水率为10%土体的滞回曲线。由图10可以看出:随着动力湿化作用的进行滞回曲线呈现明显地倾倒现象,这表明土体的回弹能力正在逐渐衰减。
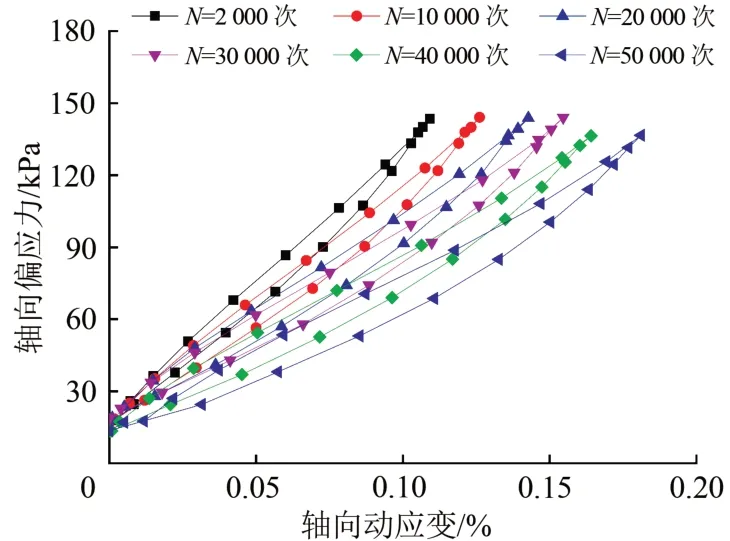
图10 K=0.96,w=10%时土体的滞回曲线
鉴于压实系数对土体抗变形能力的显著影响,将不同振次下、不同压实系数土体的滞回曲线平移至原点进行对比,如图11所示。由图11可以看出:3 种压实系数土体的回弹能力在动力湿化过程中发生明显变化,压实系数为0.96 的试样在动力湿化全程皆具有明显强于其余2 种压实系数土体的回弹能力;而压实系数为0.9和0.93的试样,在加载次数N<10 000 时的滞回曲线近似重合,表明两者回弹能力相近,当加载次数超过10 000次,并逐渐递增至40 000 次的过程中,2 种压实系数土样的滞回曲线斜率差异逐渐明显。
对比图10和图11的滞回环面积发现:土样在加载次数逐渐递增至50 000次的过程中,滞回环面积变大,这表征随着加载次数的增多能量耗损增大;但对处于同一动力湿化进程的土样,压实系数为0.96 土体的滞回环面积小于压实系数为0.9 和0.93 的面积,这表明压实系数较大的土样能量耗损较小。
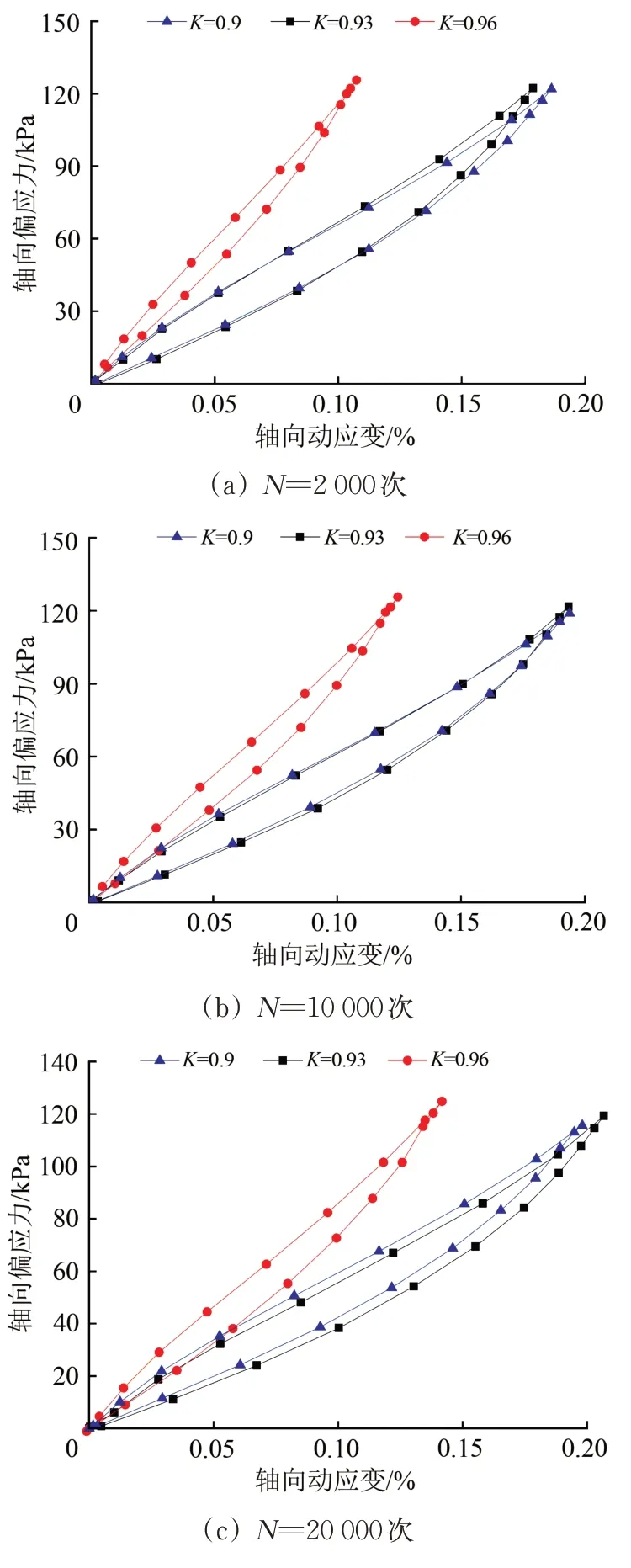

图11 w=10%,σd=120 kPa时土体滞回曲线
图12为不同初始压实系数、不同含水率的土体在动力湿化作用下的动回弹模量与加载次数的关系曲线。由图12可以看到:随着动力湿化作用的进行,土体动回弹模量持续衰减,这是由于在水体侵蚀与动载破坏的耦合作用下,土体结构不断遭到破坏,从而导致土体的抗变形能力被不断削弱;不同初始压实系数土体的动回弹模量衰减规律差异显著,压实系数分别为0.9,0.93,0.96 的土体动回弹模量分别衰减22%,32%,42%;压实系数为0.96 的土体,虽然衰减程度较大,但衰减后的动回弹模量仍明显高于其余2 种压实系数的土体;压实系数为0.93 的土体,虽然未浸水前的动回弹模量稳定值大于压实系数为0.9 的土体,但在浸水后的衰减过程中,动回弹模量逐渐低于压实系数为0.9 的土体;在动力湿化阶段,不同初始含水率土体的动回弹模量衰减规律相似。
4 动力湿化作用下动回弹模量软化模型
4.1 模型的构建与拟合
本文基于动力湿化试验数据和Idriss 软化指数模型[19]的构建思路,为动力湿化阶段构建动回弹模量软化指数,定义如下:
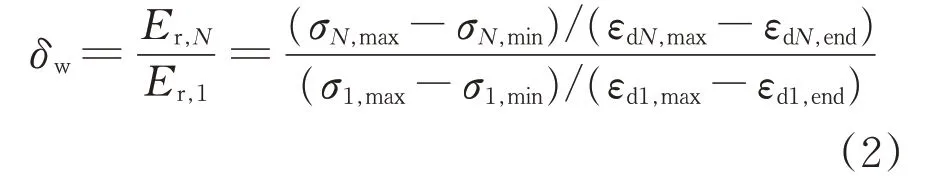
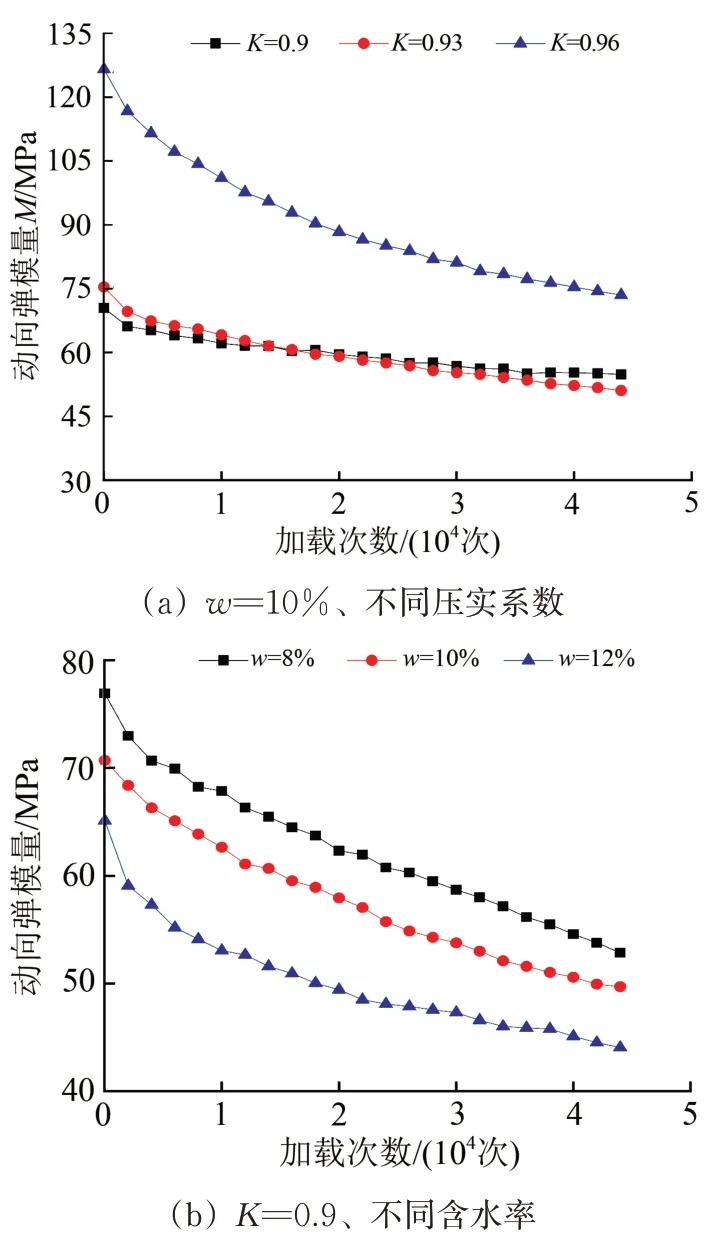
图12 动回弹模量—加载次数关系曲线
式中:δw为湿化作用下动回弹模量软化指数;Er,N为第N次加载时的动回弹模量;Er,1为第1 次加载时的动回弹模量;σN,max,σN,min分别表示第N次加载循环时的偏应力最大值和最小值;εdN,max,εdN,end分别为第N次加载循环时的动应变最大值和卸载末应变值;σ1,max,σ1,min分别表示第1 次加载循环时的偏应力最大值和最小值;εd1,max,εd1,end分别为第1次加载循环时的动应变最大值和卸载末应变值。
由于当前对于土体软化机理研究的匮乏,尚不能从理论上推导出土体软化模型,只能根据试验结果进行模拟分析。本文对动力湿化阶段的试验数据进行拟合分析,得出软化指数与循环加载振次的关系式

式中:a和b为与土样类型、性质及应力水平有关的试验常数。
由于压实系数对动回弹模量软化规律有显著影响,对不同压实系数土体的试验数据进行拟合,如图13所示。由图13可以看出,模型拟合参数a和b随着压实系数的增大而增大。由此建立动力湿化作用下的动回弹模量软化模型
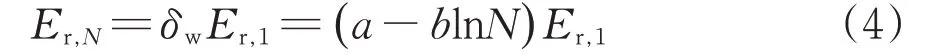
4.2 模型应用
为验证模型合理性与可推广性,本文根据所得模型编写算法,并在相同的初始条件与加载条件下,采用朔黄铁路原平工务段现场所取土体进行试验,土体基本物性参数见表2。图14给出了压实系数为0.9 的土体在不同初始含水率状态下的动回弹模量试验值和拟合曲线。由图14可以看出,本文提出的模型可以很好地反映土体在动力湿化作用下的动回弹模量衰减规律。
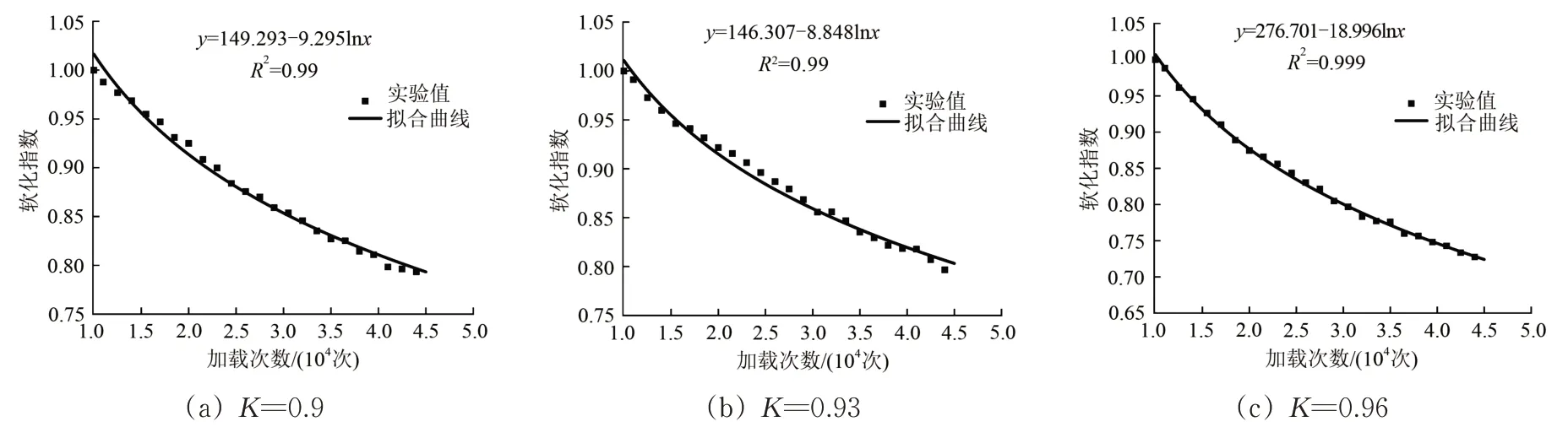
图13 w=10%时不同压实系数下的软化指数模型拟合曲线

表2 试样物性参数
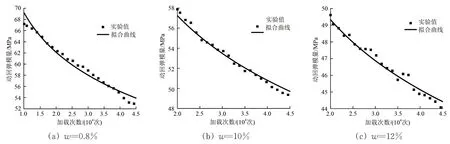
图14 K=0.9时不同含水率下的动回弹模量试验值和拟合曲线
5 结论及建议
(1)在动力稳定阶段的前100 次循环加载中,动回弹模量增长幅度较大,随后逐渐趋于稳定;压实系数越大、含水率越低的土样的累积塑性变形越小,且当其达到动力稳定状态后的动回弹模量越大。
(2)浸水后,动回弹模量明显衰减,且压实系数越大的土体衰减程度越大,压实系数分别为0.9,0.93,0.96 的土体动回弹模量分别衰减22%,32%,42%;不同初始含水率的土体动回弹模量衰减规律相似。
(3)在Idriss 软化指数模型的基础上,以动回弹模量进行软化指数的构建,并建立动力湿化作用下的土体刚度软化模型。该模型能够反映土体刚度受压实系数的显著影响,模型拟合参数随着压实系数的增大而增大。应用表明该模型具有较好的适用性,可以较为准确地预测土体软化规律。
