运营期高速铁路轨道长波不平顺静态测量方法及控制标准

杨 飞，赵文博，高芒芒，孙加林

（中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081）

轨道不平顺包含不同的波长成分,不同波长成分对列车运行安全性、舒适性的影响也不相同［1-2］。列车速度越高,影响列车动力响应的轨道不平顺波长也越长。由于轨道长波不平顺整治比较困难,并且动态检测较为复杂,因此对于疑似是由长波不平顺引起的“晃车”区段,应首先对其进行静态测量复核。

我国对轨道长波不平顺的静态测量主要借鉴德国的矢距差法［3］。由于矢距差法计算模型较为复杂,日常检测时常常对其简化,利用简化的矢距差公式对轨道长波不平顺进行评价。随着我国高速铁路运营年限的增加,以及受外界环境因素的影响,部分高速铁路基础已出现较大的变形问题［4］,采用现有的矢距差法或者简化矢距差法测量,结果都明显超出验收标准,而我国又无运营期高速铁路轨道长波不平顺静态控制标准,且超过验收标准的区段大部分列车实际运营状况良好,如综合检测车检测的动态轨道长波不平顺和车辆振动加速度均无明显响应,使高速铁路运营时现场维修部门无法准确查找确实有影响的轨道长波不平顺,导致复核及养修的不便利。

对于轨道长波不平顺,国外其他国家如日本选用40 m 弦对新干线轨道进行测量［5］。法国采用与日本一样的测量方法,认为2 个转向架之间的总长约为33 m,只要控制好33 m 弦测量得到的幅值就能保证行车的舒适性,因此法国采用了高低31 m弦、轨向33 m 弦测量结果评价轨道长波不平顺。韩国建议高速铁路25 m以上波长不平顺应采用30 m或40 m长弦进行测量［6］。

本文在分析现有高速铁路轨道不平顺静态测量方法的基础上,采用实测数据及理论分析相结合的手段,研究国内现行高速车辆动力响应与轨道不平顺的匹配关系,提出更为准确的轨道长波不平顺静态测量方法及相应幅值控制标准。

1 现有测量方法

1.1 矢距差法

矢距差法通过计算一定弦长范围内各测点间的相对点位关系评价轨道平顺性,目前我国主要通过300 m（480a,其中a为扣件间距）弦长范围内、相距150 m（240a）任意2 个测点间的矢距差评价静态轨道长波不平顺［4］,测量示意图如图1所示。图中：Pi为轨枕测点编号,i=0,1,2…；ri为第i测点处的矢距。

图1 矢距差法测量示意图

矢距差法计算轨道不平顺的公式为

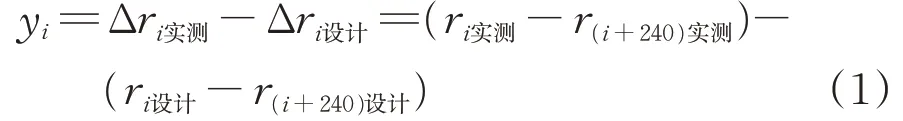
式中：yi为矢距差法检测的第i测点处轨道不平顺；Δri实测为第i测点处轨道不平顺实测矢距差；Δri设计为第i测点处轨道不平顺设计矢距差；ri实测和ri设计分别为第i测点处的实测和设计矢距。

1.2 简化矢距差法

矢距差法计算的矢距垂直于测弦,属于轨道内部几何参数［7］,与轨道精调时沿线路横向和垂向调整不一致,容易引起混淆。而现场多通过测量轨道高程偏差、中线偏差等外部几何参数对轨道不平顺进行评价,因此需要将内部几何参数转换成需要的外部几何参数,转换模型如图2所示。图中：Pi’为各测点设计编号；α为测弦两端点与水平基准面的夹角（近似等于0）。

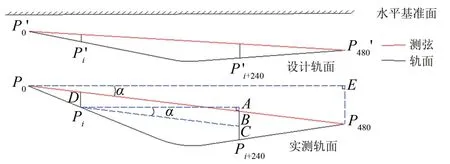
图2 矢距差法计算模型

根据式（1）,利用图2中几何关系得

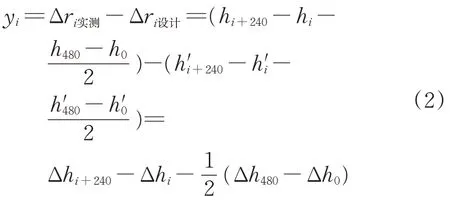
式中：hi为实测轨面测点至水平基准面的高程；hi’为设计轨面测点到水平基准面的高程。

式（2）将测量结果中的矢距转换成了轨道高程,既简化了计算,又使得物理模型更加清晰。其中,等式右边第1 项为第i+240 测点高程变化量,第2 项为第i测点高程变化量,第3 项为测弦两端点高程变化量之差。当测弦上2 个端点轨道高程变化量之差相等时,即轨道结构在测弦范围内均匀变形时,第3项等于零,矢距差法可以简化为

式（3）为轨道不平顺的简化矢距差法计算公式,为现场测量中常用的计算方法,用间隔150 m（240a）的2个测点的高程变化量之差表示矢距差。

1.3 测量方法适用性

1）传递函数检验

实测轨道不平顺数据经过采用矢距差法处理后得到新的轨道不平顺数据,输入的实测轨道不平顺幅值与输出的新的轨道不平顺幅值之间的关系可以用传递函数表示。由于轨道不平顺为随机不平顺,包含不同的波长成分,为研究不同波长轨道不平顺经过矢距差法处理后的幅值及相位变化,需要对式（2）和式（3）作傅里叶变换,可分别得到矢距差法和简化矢距差法的传递函数H（ω）。

采用矢距差法时,

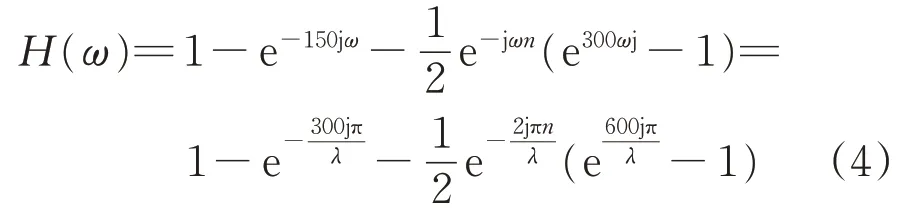
式中：ω为空间角频率,rad·m-1,ω=2π/λ；λ为轨道不平顺波长；j为虚数。

采用简化矢距差法时,

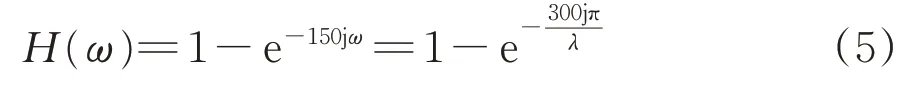
从式（4）和式（5）看出,2 种计算方法得到的传递函数都包含虚部,即测量结果与实际轨道不平顺存在相位差,表现为轨道不平顺的测量位置并非其实际位置,有一定的偏移。

对2 种方法的传递函数幅频响应进行计算,结果分别如图3和图4所示。由图3和图4可以看出：矢距差法传递函数的幅频响应受轨道不平顺波长和测点位置的共同影响,幅频响应在-0.42～2.4 之间振荡；简化矢距差法传递函数的幅频响应只受轨道不平顺波长的影响,与测点位置无关,幅频响应在0～2之间振荡。

2）实测数据检验

图3 矢距差法传递函数

由于以上分析主要考虑了运营期高速铁路路基变形问题,因此主要针对路基变形引起的轨道垂向变形及相应车辆的垂向振动进行研究,后续若未特别说明,“轨道不平顺”和“车体加速度”均指的是“轨道高低不平顺”和“车体垂向振动加速度”。选取某段运营期高速铁路,分别利用矢距差法和简化矢距差法计算轨道不平顺,同时截取相应区段综合检测车检测的车体加速度进行对比,结果如图5所示。图中：g为重力加速度。

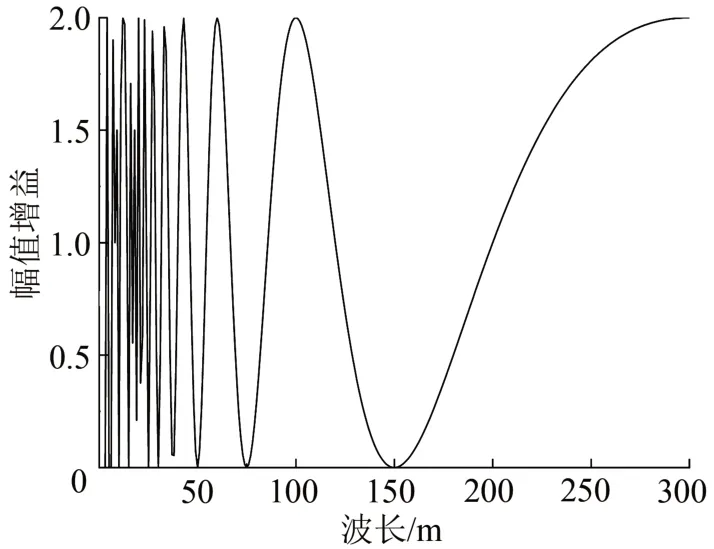
图4 简化矢距差法传递函数

由图5可以看出：整个区段根据轨道不平顺大致可以分为区段1 和区段2,区段1 轨道不平顺幅值明显大于区段2,但是2 个区段的车体加速度差别不大；点A3的车体加速度大于点B3,然而矢距差结果却是点A1小于点B1,尽管简化矢距差法测量结果中点A2大于点B2,但是车体通过点A和点B这2 个位置时车体加速度与轨道不平顺并无明显相关性；另外,从区段1 轨道不平顺数据可以看出,简化矢距差法测量结果明显大于矢距差法,且2 种方法的测量结果都远远超过高速铁路无砟轨道维修规则规定的10 mm/150 m/300 m 限值（即300 m弦长,间隔150 m,2个测点矢距差不超过10 mm）。以上结果都说明矢距差法和简化矢距差法测量结果与车体动力响应匹配性较差,不适用于运营期高速铁路轨道长波不平顺的静态测量。

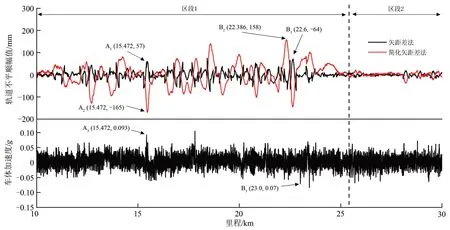
图5 不同方法得到的轨道不平顺与车体加速度相关性

2 60 m 弦中点弦测法

2.1 中点弦测法

我国目前采用测弦长度为10 m 的中点弦测法（简称10 m 弦中点弦测法）进行轨道中波不平顺的静态测量,其测量示意图如图6所示。图中：L为半弦长,则测弦长度为2L。在计算时,由于测弦长度远大于测弦两端点高程偏差,因此检测时测弦与水平基准面夹角很小［8］,此时yi可近似为中点弦测法矢距,为

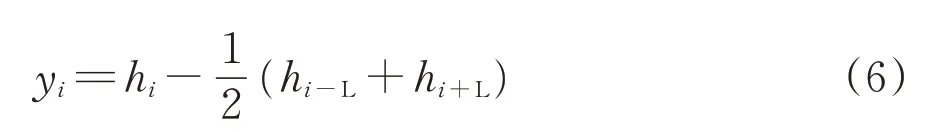
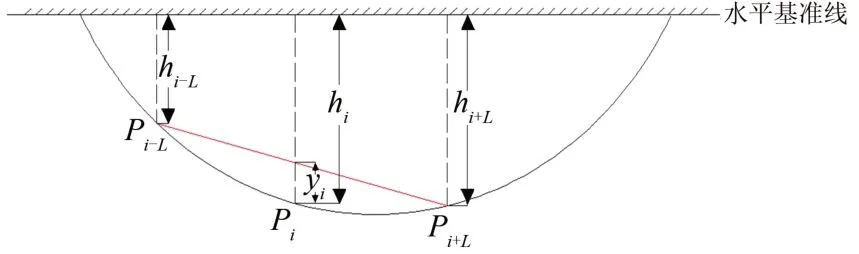
图6 10 m中点弦测法测量示意图

2.2 60 m弦中点弦测法

由式（6）可以看出,采用中点弦测法时测量结果受测弦长度2L的影响,不同测弦长度测量轨道不平顺结果不同,因此需要选取合理的测弦长度。车体动力响应受轨道不平顺的影响,尤其是当轨道不平顺波长在列车敏感波长附近时,车体振动剧烈,因此弦测法测量轨道不平顺波长范围应涵盖列车敏感波长,而不同测弦长度能够测量的有效波长范围不同,因此需要结合中点弦测法不同测弦长度有效测量波长范围以及列车敏感波长确定中点弦测法合理的测弦长度,具体流程如图7所示。

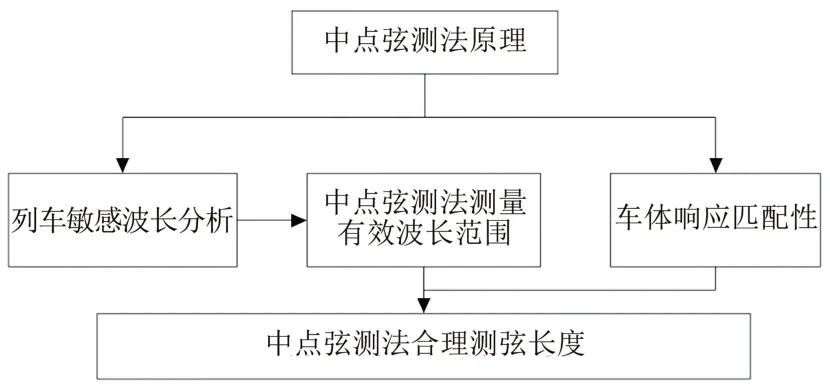
图7 中点弦测法合理的测弦长度确定流程

1）不同测弦长度测量有效波长范围

中点弦测法采用固定测弦长度进行测量,因此对于过长或过短波长的轨道不平顺不能有效测量［9-10］,其有效测量范围可根据传递函数进行计算。根据式（6）可得传递函数表达式为

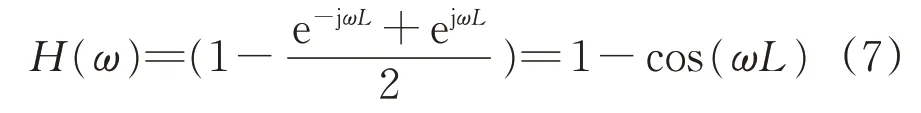
由式（7）可以看出,中点弦测法传递函数受轨道不平顺波长λ（λ=2π/ω）和测弦长度L的影响,且传递函数中不存在虚部,说明测量结果与实际结果不存在相位差,可以准确测得实际位置的轨道不平顺。

分别采用10,40 和60 m 测弦长度时得到的轨道不平顺波长和幅值增益的关系如图8所示。从图8可以看出：中点弦测法传递函数在0～2.0 之间,若以传递函数不小于1.0 为有效测量,可分别得出10,20,30,40,50 和60 m 弦对应的有效测量波长范围分别为7～20,13～40,20～60,27～80,33～100和40～120 m。

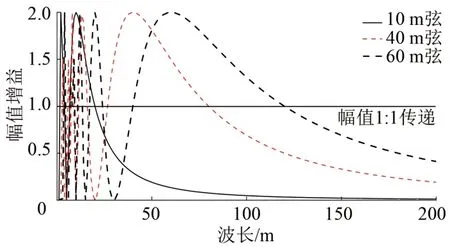
图8 中点弦测法有效波长范围

2）列车敏感波长

收集综合检测车2 次检测数据,选取某运行速度为300 km·h-1区段,得到车体加速度功率谱密度如图9所示。由图9可以看出：低频区段车体垂向振动加速度空间频率集中分布在0.013 67～0.015 63 Hz 范围内,对应波长为64～73 m,该波长即为车速300 km·h-1时的车体垂向敏感波长；低频区段车体横向振动加速度空间频率集中分布在0.009 8 Hz 附近,对应波长为102 m,该波长即为速度300 km·h-1时的车体横向敏感波长。

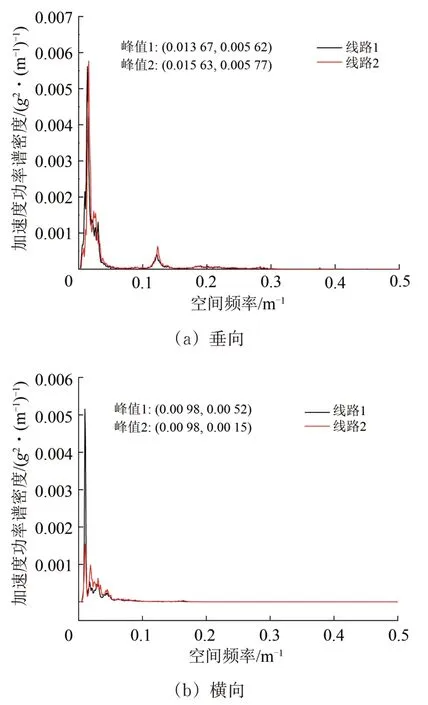
图9 综合检测车车体振动加速度功率谱密度

对于同一型号列车,车体自振频率一定,根据列车敏感波长与运行速度的关系即式（8）可看出,影响列车振动的轨道不平顺波长随着速度的提高而增大。

式中：λs为敏感波长,m；v为列车速度,km·h-1；f为车体自振频率,Hz。

已知速度300 km·h-1列车敏感波长,可以得出速度350 km·h-1列车敏感波长,结果见表1。从表1可以看出：对于现行速度最高为350 km·h-1线路,轨道不平顺管理波长应不小于120 m,而测弦长度为60 m 时中点弦测法（简称60 m 弦中点弦测法）的有效测量波长范围为40～120 m,因此确定测弦长度为60 m,即可满足轨道不平顺管理波长的要求。

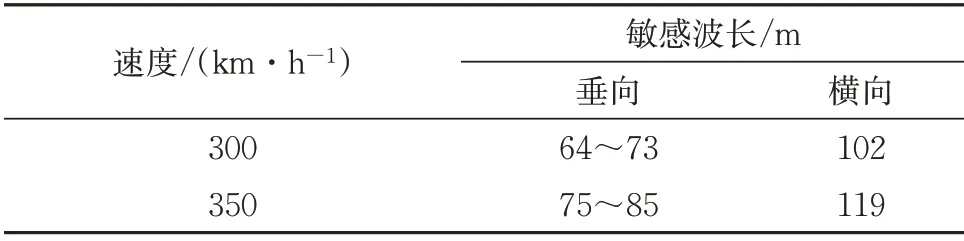
表1 不同速度时的列车敏感波长

3）车体响应匹配性

中点弦测法计算公式具备2阶差分的形式,与轨道不平顺的2阶导数相关,从动力学角度来看,中点弦测法结果形式与车体加速度一致,因此需要研究中点弦测法轨道不平顺与车体加速度的匹配性。采用包括适用于轨道中波不平顺静态测量的10 m弦等不同弦长测量轨道不平顺,并与车体加速度进行对比,结果如图10所示。从图10可以看出：10 m 弦测量的轨道不平顺与车体加速度相关性较差,40 m弦和60 m 弦测量的轨道不平顺与车体加速度相关性较好。

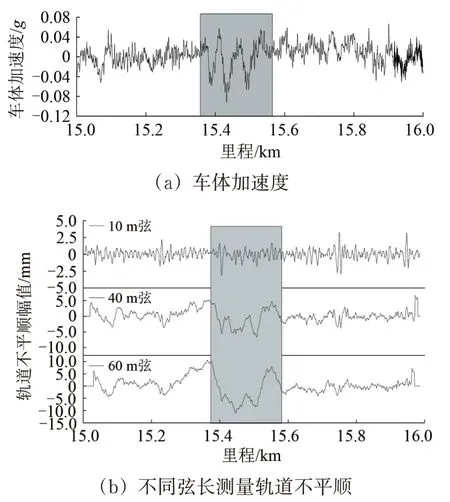
图10 不同弦长中点弦测法测量轨道不平顺与车体动力响应对比

同理,对多个检测区段采用不同测弦长度得到的轨道不平顺测量结果与车体加速度相关性进行分析,得到相关系数均值见表2。从表2可以看出：40,50 和60 m 弦轨道不平顺测量结果与车体加速度的相关性明显优于10,20和30 m弦。

表2 相关系数均值

以上对矢距差法、简化矢距差法及不同测弦长度中点弦测法的计算原理及特性进行了分析,为得出评价轨道长波不平顺的合理方法,需对以上方法的优劣性及适用性进行对比,结果汇总见表3。

表3 不同测量方法的优劣性

从以上分析得出：矢距差法和简化矢距差法都存在相位差,导致测量结果偏离实际位置,且测量结果明显大于实际轨道不平顺；此外,由于运营期高速铁路路基存在不均匀变形,从原理上来说矢距差法不能进行简化；10 m 弦中点弦测法由于测弦长度太短,不能有效测量长波不平顺,导致测量结果与车体动力响应匹配性较差,因此都不适用于运营期高速铁路轨道长波不平顺静态检测；60 m 弦中点弦测法检测特性明显优于以上几种方法,且有效测量轨道不平顺波长范围为40～120 m,满足列车敏感波长及轨道长波不平顺管理波长的需要,因此建议采用60 m 弦中点弦测法对运营期轨道长波不平顺进行静态测量。

3 轨道长波不平顺控制标准

收集综合检测车在速度为300 km·h-1时的检测数据,采用60 m 弦中点弦测法可以得到一系列轨道不平顺及对应的车体加速度数据,同1个轨道不平顺会得到1组对应的车体加速度,为保证行车安全性和乘客舒适性,统计每个轨道不平顺所对应的1组车体加速度的均值、标准差,在95%置信区间下求每个不平顺幅值所对应的最大可能加速度,并研究车体加速度与轨道不平顺幅值之间的关系,如图11所示。从图11可以看出：车体加速度与轨道不平顺近似呈线性关系,采用最小二乘法进行拟合,得出时速为300 km 时车体加速度与轨道不平顺幅值之间的关系为车体加速度=0.008×轨道不平顺+0.028。

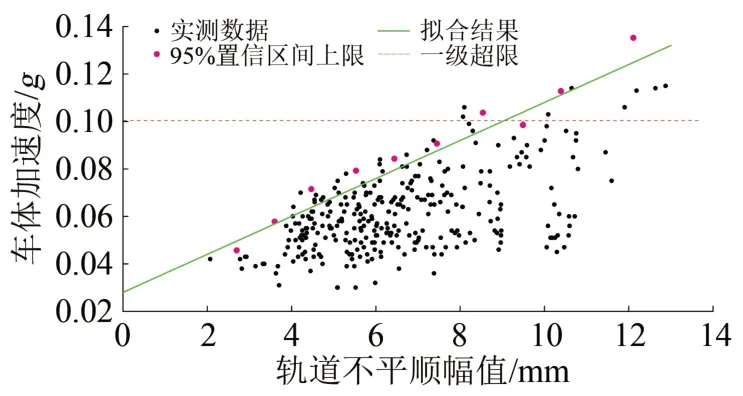
图11 轨道不平顺与车体加速度关系

以车体加速度为控制标准,得出60 m 弦中点弦测法测量运营期高速铁路轨道长波不平顺控制标准建议值见表4。

表4 时速300 km运营期高速铁路60 m弦中点弦测法的轨道长波不平顺控制标准建议值

由于实测350 km·h-1检测数据较少,不能采用统计方法,基于以上300 km·h-1控制值,需要研究列车运行速度与加速度之间的关系,进而推断速度为350 km·h-1时的控制标准建议值。日本根据运营经验得出,车体振动加速度的增幅可按照正比于列车速度1.5次方来推断［11］,即

式中：a1和a2为车体加速度；v1和v2为列车速度。

利用多体动力学仿真软件UM建立车辆动力学仿真模型,如图12所示。

图12 车辆动力学仿真模型

设置余弦型不平顺［12］,波长一定,幅值为10～30 mm,计算各种速度工况下,车体加速度与速度的关系,结果如图13所示。从图13可以看出：对于速度分别350 和300 km·h-1,车体加速度比约为速度比的1.25 倍,与式（9）计算结果1.26 基本一致。

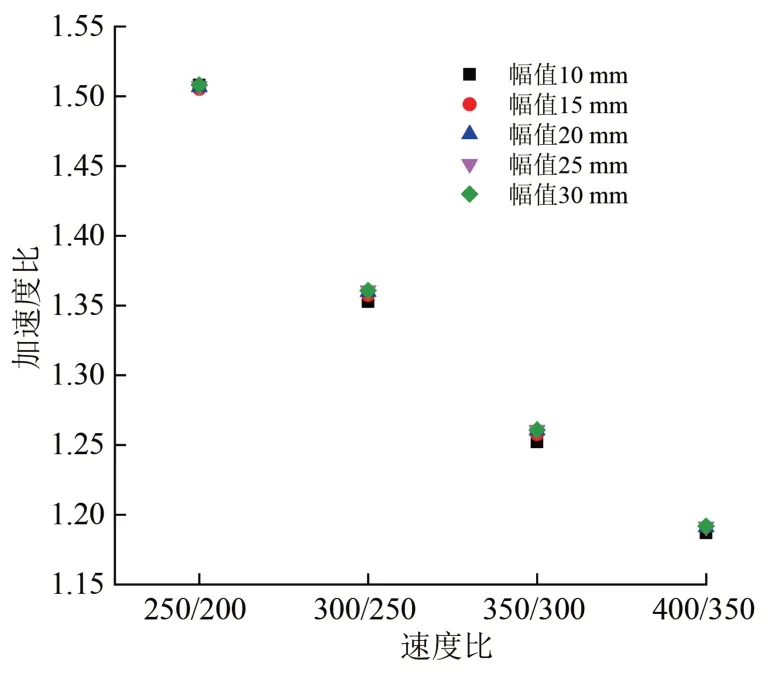
图13 不同轨道不平顺下加速度比与速度比关系

因此可以根据表4及车体加速度与列车速度之间的关系,以车体垂向加速度为控制指标［13］,得出速度为350 km·h-1,60 m弦中点弦测法测量运营期高速铁路轨道长波不平顺控制标准建议值见表5。

表5 时速350 km运营期高速铁路60 m弦中点弦测法的轨道长波不平顺控制标准建议值

4 实例验证

60 m 弦中点弦测法可通过轨检仪矢距测量系统利用“以小推大”进行测量得到,也可基于CPIII 控制网通过轨测仪先测得轨面绝对位置,然后利用式（6）计算获得,后一种方法精度较高。某运营期高速铁路区段轨测仪检测得到的实测轨面高程偏差如图14（a）所示,得到的60 m 弦中点弦测结果如图14（b）所示。

为验证60 m 弦测法的有效性,对上述区段按照350 km·h-1检测标准进行评价,得出部分超限区段,其中K58+175 区段轨道高低不平顺波形如图15所示。由图15可以看出,轨道长波高低不平顺最大幅值达到10.65 mm。

图14 实测轨面高程与中点弦测法结果对比

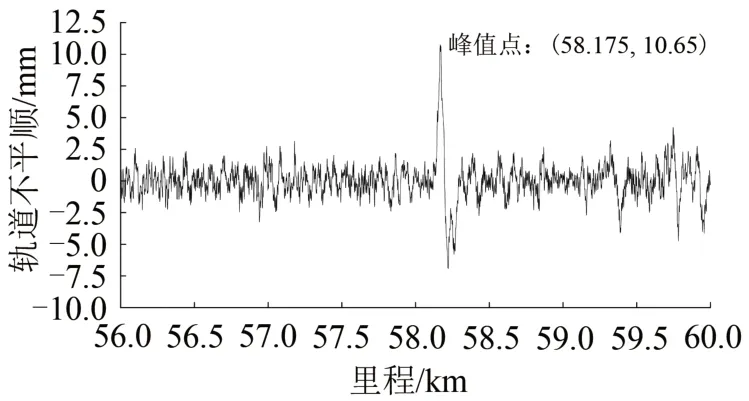
图15 60 m弦中点弦测法测量结果

综合检测车以速度292 km·h-1对本区段进行检测,动态检测结果如图16所示。由图16可以看出,轨道长波高低不平顺峰值为8.5 mm,同样超过动态检测Ⅰ级维修标准,车体加速度达到0.098g,基本接近Ⅰ级标准［14］,表明60 m 弦中点弦测法测得的轨道长波不平顺与车体振动加速度匹配性较好,可以准确发现影响运营舒适性的区段。

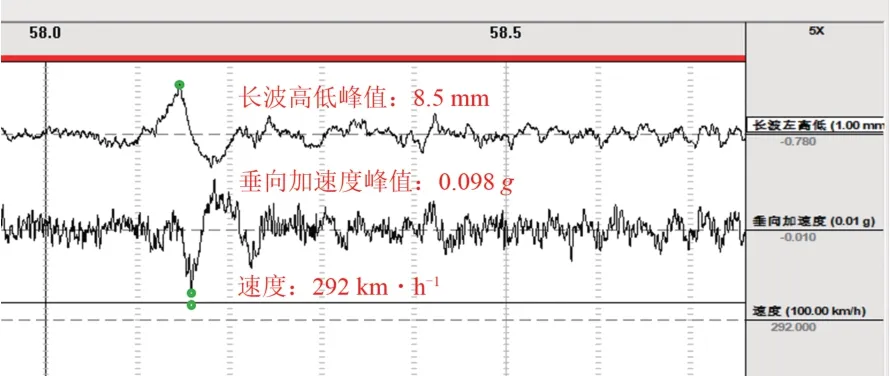
图16 动态检测结果

针对以上区段,现场根据60 m 弦中点弦法的测量结果进行了及时维修,得到维修后60 m 弦中点弦测结果如图17所示。由图17可以看出：轨道长波高低不平顺幅值明显降低,在K58.175区段附近最大值为4.9 mm,出现在K58+337 处,低于轨道长波高低不平顺Ⅰ级维修标准。

综合检测车以352 km·h-1速度对本区段进行检测,结果如图18所示。由图18可以看出,维修后轨道长波高低不平顺峰值为1.27 mm,车体垂向振动加速度峰值0.04g,均远低于动态检测Ⅰ级维修标准,表明60 m 弦中点弦测法测得的轨道长波不平顺可以较好地指导现场养护维修。

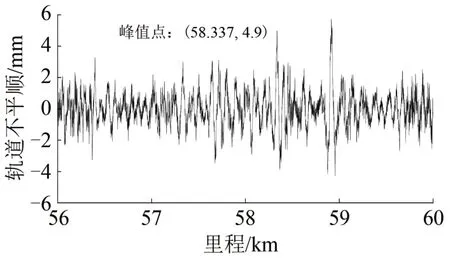
图17 维修后60 m中点弦测结果

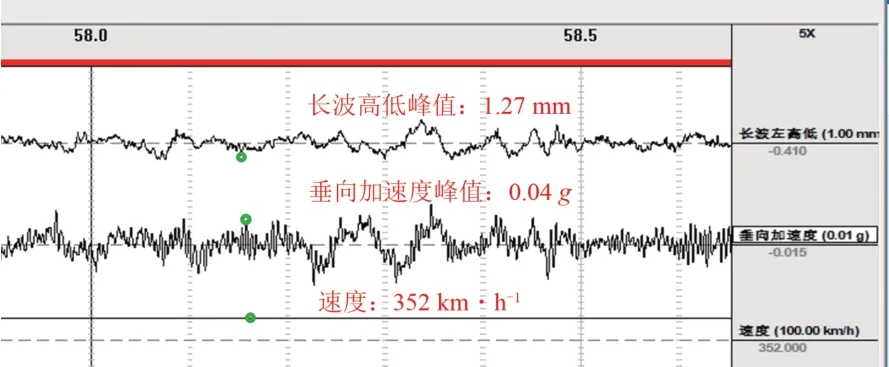
图18 维修后动态检测结果

5 结 论

（1）根据矢距差法、简化矢距差法的检测特性以及实测数据分析,可知现有轨道长波不平顺测量方法与实际结果存在与检测起点相关、含有里程相位差、基础变形时检测幅值偏大、与车体振动加速度匹配性较差等问题,不适用于运营期高速铁路轨道长波不平顺的静态检测。

（2）中点弦测法测量结果与车体加速度匹配性较好。根据加速度谱分析,影响车体响应的最大不平顺敏感波长接近120 m；从中点弦测法测量有效波长范围以及不同弦长与车体加速度相关性可以知道,选用60 m弦中点弦测法既可以满足轨道不平顺管理的需要,又可以很好地与车体动力响应匹配。因此,建议选用60 m 弦中点弦测法作为我国时速300～350 km高速铁路轨道长波不平顺静态测量方法。

（3）利用60 m 弦中点弦测法得到的轨道不平顺与车体振动加速度的关系,以及车体振动加速度与速度的关系,给出速度300 km·h-1运营期高速铁路60 m 弦中点弦测法的轨道长波高低不平顺3级控制标准建议值分别为9,15,21 mm；借助动力学仿真分析,推演出速度350 km·h-1运营期高速铁路60 m 弦中点弦测法的轨道高低不平顺3 级控制标准建议值分别为7,11,15 mm。

（4）利用提出的60 m 弦中点弦测法对实际运营期线路进行评价,结果表明采用该法得到的轨道长波不平顺与车体振动加速度匹配性较好,可以准确地发现影响运营舒适性的区段；利用60 m 弦中点弦测法测量结果开展维修工作,可以使轨道不平顺幅值明显降低,起到了更好地指导现场养护维修工作的效果。