无砟轨道—路基结构相似模拟试验研究
2020-06-10赵如锋赵国堂
赵如锋,赵国堂,杨 斌,赵 磊
(1.北京交通大学 土木建筑工程学院,北京 100044;2.中国国家铁路集团有限公司,北京 100844;3.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081)
随着高速铁路的大量建设,各种不良地质环境引起的轨道问题也逐步显露。当无砟轨道铺设于基础稳定性较为薄弱的区域,如差异沉降区、膨胀土、路基冻胀变形量较大等区域[1],基础变形将直接影响轨道平顺性以及无砟轨道受力,较为剧烈的差异沉降会导致层间动态离缝和脱空,影响行车舒适性和安全性。路基变形影响研究成为高速铁路路基上无砟轨道研究的难点问题。
对于轨道—路基模型试验而言,轨道结构对路基变形响应的理论研究进展相当有限。陈兆玮,孙宇,翟婉明等[2]通过解析方法分析了双块式无砟轨道、CRTSⅡ型板式无砟轨道桥梁墩台变形与轨面不平顺之间的映射关系;蔡小培、赵立宁等[3]研究了地面沉降引起的路基上单元板式和双块式无砟轨道轨面变形问题,对比了几种常见地面沉降对无砟轨道结构平顺性的影响;陈鹏、高亮等[4]针对地面沉降开展无砟轨道结构平顺性研究,分析了不同形式地面沉降引起的轨道结构变形。赵磊[5]分析了过渡段路基上拱对大单元双块式无砟轨道受力及行车动力影响。可以看出,基础变形对无砟轨道影响的分析多停留在理论分析层面,侧重点多针对轨面平顺性及行车动力响应,而针对基础变形在路基内部传递规律及其对无砟轨道受力影响方面的理论研究不足,基础变形对无砟轨道影响的试验研究尚属空白。
高速铁路路基土体的受力复杂,变形传递过程也并非既有的弹性模型或塑性、弹塑性模型能够真实模拟,加上无砟轨道层间相互作用关系也极为复杂,目前尚缺乏合理的模型能够对无砟轨道层间相互作用关系进行真实模拟。
要掌握基础变形对无砟轨道轨面平顺性及轨道受力的影响过程,必须首先掌握现场条件下基础变形传递至路基表面、无砟轨道及轨面的实际变形传递过程,并对基础变形过程中无砟轨道各层的荷载效应及离缝特征进行监测。相似模拟试验在采矿工程[6-8]、隧道工程[9-11]、路基工程[12-16]均有大量应用,为获取真实结构在荷载下的响应提供了有价值的参考。然而,相似模拟试验在无砟轨道方面尤其是基础变形对无砟轨道影响研究方面尚无应用。
本文在无砟轨道—基础变形仿真分析的基础上,采用量纲分析法,进行建立包含下部基础的无砟轨道相似试验仿真模型研究。
1 相似模型设计准则
当所研究问题的参数较多且相互关系复杂,无法得出各参数间的解析关系时,可采用量纲分析法确定相似准则和相似指标。
量纲分析法是用量纲方程表示物理方程,根据量纲方程等号两边量纲齐次性,解出物理方程式中各物理量的未知幂指数。本相似试验模型中所包含的物理量有:
(1)结构几何尺寸l;
(2)结构上荷载,包括自重(用重度γ表示)和位移荷载Fy;
(3)结构反应,包括挠度δ、应力σ和应变ε;
(4)材料性能,包括弹性模量E和泊松比ν,扣件刚度k。
假定上述9个物理量之间存在的函数关系为

选定力量纲[F],长度量纲[L]作为基本量纲,上述9个物理量与其对应的量纲关系见表1。

表1 各物理量与基本量纲的关系
选取γ和E组成基本量群,令式(1)中其他量纲与此基本量群的量纲相除,得到

式中:π1—π7均为无量纲量。
以π1为例说明其求解,

为使π1为无量纲量,则式中未知量a和b需满足

由式(4)可得a=-1,b=1,代入式(3)可得到

同理可得到π2—π7表达式,汇总得相似判据

因此,在模型设计中若能满足式(7)中条件,则模型满足量纲相似。

式中:m表示模型;p表示原型。
根据量纲相似设计原则,当原型与模型尺寸比例为1:n时,若材料弹性模量比例1:n、加载位移比例为1:n、重度γ 比例为1:1、扣件刚度1:n2时,满足量纲相似,此时结构变形比例为1:n,应力比例为1:n;若材料弹性模量1:1,加载位移比例为1:n,重度γ比例为n:1时,亦满足量纲相似,此时结构变形比例为1:n,应力比例为1:1。
2 相似模型的验证
依据上述相似模型设计原则分别建立不同比例参数的无砟轨道—路基变形仿真分析模型,对所获取的相似模型设计原则进行验证。模型自上而下包含钢轨、扣件、轨道板、自密实混凝土、底座板、基床以及地基,共建立如下4个模型。
模型1:无砟轨道—路基实尺分析模型。
模型2:无砟轨道—路基直接缩尺模型(仅尺寸缩放的非相似模型)。
模型3:无砟轨道—路基尺寸1:4 相似分析模型,弹性模量比例1:4(通过弹模比例达到模型相似)。
模型4:无砟轨道—路基1:4 比例分析模型,材料重度比例4:1(通过重度比例达到模型相似)。
建立的CRTSⅢ型板式无砟轨道及下部路基模型如图1所示。建立的4 个对比模型参数见表2和表3。实尺模型总长85.3 m,加载波长20 m,最大加载量40 mm;比例模型总长21.3 m,加载波长5 m,最大加载量10 mm。
利用仿真分析软件对原型、直接缩尺模型、2种相似模型的荷载响应进行静力分析。在模型2、模型3、模型4 中,对地基底面施加5 m(1:4)波长的沉降变形,将计算结果中尺寸与位移放大4 倍,应力比例尺仍为1:1,与模型1 进行对比,结果如图2—图6所示。

图1 CRTSⅢ型板式无砟轨道及下部路基模型

表2 无砟轨道结构参数

表3 下部基础结构参数

图2 轨道板竖向位移

图3 底座板竖向位移

图4 基床表层竖向位移

图5 轨道板表面纵向应力

图6 底座板表面纵向应力
通过4 种模型荷载响应对比分析可以得出,采用直接缩尺模型时,基础变形曲线吻合较好,但轨道板及底座板变形与实尺模型间差异较大,轨道板及底座应力分布也与实尺模型差异较大。当改变结构中材料弹性模量的比例或材料重度的比例达到模型相似时,基础变形所产生的无砟轨道变形及应力与实尺模型基本等比例相近。由此验证了基于量纲相似模型设计准则的准确性。
3 相似模型试验设计
3.1 相似材料比选
相似材料的选择是本试验方案中的难点,方案中涉及的主要材料有路基土体和混凝土材料2种。
对于路基土体,根据调研可知,在利用离心机进行相似模型设计时,西南交大罗强教授团队[15]做了部分简化,认为路堤部分为连续均匀、各向同性体,路堤各层采用Mohr-Coulomb 材料模拟,试验采用级配砂作为路基填料,粉体颗粒直径d50为0.4 mm、细粒含量3.9%、不均匀系数Cu为5、曲率系数Cc为1.25,属于级配良好的中砂。级配砂按照相似比例关系换算成原型填料属于级配良好的A 组粗颗粒土填料。模型的压实系数为0.95。武汉理工大学芮瑞副教授团队[16]采用内摩擦角31°,颗粒相对密度2.67 g·cm-3的干净河砂作为填料进行试验,利用填料质量控制砂的密度,将其密度控制在1.688 g·cm-3。每填砂15 kg,均匀虚铺后用夯板夯至厚度25 mm。
可以看出,既有相似模型构建时多采用砂模拟土体,为本文土体的相似材料选择提供了参考和依据。为模拟深层压缩模量较大的土体以及浅层压缩模量较小的土体,本文分别采用细砂和中砂对深层和浅层地基进行模拟。
对于混凝土材料,国内外在开展模拟试验时多采用与模拟对象材料一致的混凝土材料开展缩尺试验,主要原因是此类试验研究对象主要为混凝土材料本身的极限力学性能。本次试验对混凝土极限力学性能无要求,假定混凝土材料均为各向同性线弹性材料,选用相似材料的原则为材料弹性模量1:4,重度1:1。目前文献中主要选用的材料有:低弹模金属、有机玻璃、环氧树脂、石膏、水泥砂浆、微粒混凝土、环氧微粒混凝土等。上述材料基本可以满足不同相似比时混凝土材料的模拟应用。经比选,适合应用于此模型的是低弹模砂浆。无砟轨道板为C55混凝土,底座板为C30混凝土,弹性模量分别为36.5 GPa 和31 GPa,相似材料要达到的弹性模量在7~9 GPa之间。
本文选用了1 种掺膨润土水泥砂浆进行模拟。掺膨润土的砂浆弹性模量低,极限变形大,能适应较大变形。根据应用经验,分别使用了3种配方的膨润土砂浆进行比对和测试,具体配比见表4。
3种方案制作出的砂浆如图7所示。
从和易性角度来看,较小的水灰比差异,也会引起掺膨润土砂浆明显的黏稠度差异,其中,方案A的流动性最大,并且表层伴有轻微泌水现象,方案C 砂浆流动性较差,振捣后可满足密实度要求。方案B的和易性最好。
对砂浆弹性模量进行测试,结果如图8所示,由图8可见,3种方案砂浆7—28 d弹性模量均位于7~8 GPa,均满足试验需求,综合考虑砂浆和易性和弹性模量,本试验选用方案B来进行模拟。试验期为浇筑完成后15 d左右,对应弹性模量为7.5~8 GPa之间。

表4 3种配方膨润土砂浆配比

图7 3种方案制作的砂浆

图8 3种方案不同龄期弹性模量检测结果
3.2 试验平台设计
为获取下部基础不均匀沉降变形后轨道结构平顺性变化规律及结构受力变化规律,需设计包含轨道、路基、地基且能够模拟下部基础不均匀沉降变形的试验平台,所模拟的不均匀沉降变形能够涵盖多个变形波长及变形量。为此,本文设计方案中试验平台自下而上依次为轨道、路基、节段变形板、调整装置、试验台座。四周采用挡板进行围挡,为降低路基与围挡之间的边界效应的影响,在侧边位置处设置了滑动层,以达到对称边界的效果,如图9所示。

图9 试验台整体方案断面图
为方便基础变形的观测,试验台座设计成两端头为挡墙,侧边为立柱的方案,立柱内侧设置挡板进行围挡。其中一侧挡板为钢板,另一侧为透明有机玻璃(亚克力板),如图10所示。

图10 试验台座方案图
3.3 加载方式
节段变形板是实现基础底部变形的关键部件。为了实现不同的沉降波长,需要根据试验需求设计不同长度的变形板,变形板四角可实现上下位移以模拟基础不同的变形量。
本文中,节段变形板采用混凝土板模拟,利用不同长度的混凝土板的折线(如图11)变形模拟真实沉降中的曲线。

图11 沉降曲线模拟过程
在变形板的端部,设置了轨道板用精调爪,如图12所示,在安装时对变形板进行精调,在试验时实现竖向调整功能。单个精调爪的承载量为6 t,竖向调整范围为0~85 mm,在设置变形板竖向位置时,将精调爪的竖向初始位置设置至立柱中部,实现精调爪±40 mm的变形量。

图12 变形板端部精调爪
在进行试验时,每个精调爪位置处均设置1个千分表,如图13所示。以掌握实际试验变形的加载量。
实际加载过程控制表明,精调爪调整过程中,可以将千分表精度控制至0.2 mm 以内,满足测试需求。
3.4 模拟波长及幅值

图13 沉降控制用千分表
本文中,由于采用节段变形板的板端位移所产生的折线模拟沉降、上拱变形曲线,因此,单个沉降、上拱变形曲线最少由2 块变形板实现。考虑CRTSⅢ型板式无砟轨道的轨道板长度,本次模拟试验中选取的波长为板长的倍数,即最小模拟波长为5.6 m,对应变形板最小长度选为5.6 m/4/2=0.7 m。
同时,为尽可能减少变形板的数量,选择在一侧布置0.7 m 长的变形板,另外一侧均布置2×0.7 m=1.4 m 长的变形板,短波长的沉降、上拱变形均在短的变形板一侧实现。变形板的大致布置如图14所示。

图14 变形板间隔布置图(单位:mm)
当模拟基础变形(含上拱与沉降变形)时,分别模拟了2 块、4 块和6 块变形板范围内基础变形,具体基础变形调整位置如图15所示。

图15 沉降变形调整位置
目前基础变形的控制标准在15 mm/20 m,而根据过渡段轨面坡度不超过1‰的控制标准推导,在模拟的近40 m 轨道—路基模型中,不均匀变形量也不得超过40 mm,因此,本文基础变形加载量取为±15 mm,模拟的基础变形量为±60 mm,涵盖既有变形控制标准与现场调研所获取的最大不均匀变形量。
3.5 路基变形模拟试验测试方法
为了测试基础变形过程中,变形在路基内部以及传递至无砟轨道表面的扩散过程,需要在试验填筑路基内部设置可以捕捉不同位置处竖向变形的多层位移传感器。本文在充分调研相对变形测试方法的基础上,提出了用全向位移计和物位计2 种方法对基础变形扩散过程及对无砟轨道的影响进行测试。
为确保试验结果准确,将试验用全向位移计及物位计布置于同一层相同位置处相互校验。传感器均在模拟地基内布置,共3层,最底层布置在变形板表面,中间层布置于地基高度0.5 m 位置处,顶层布置于地基高度1 m 位置处。纵向上传感器对应布置在节段变形板缝位置处。具体布置方案如图16所示。
按照地基土厚度施工过程,分阶段安装传感器,传感器现场安装情况如图17所示。
4 试验结果验证

图16 传感器布置图(单位:mm)

图17 传感器现场安装
为分析路基传递规律测试结果,建立与现场试验模型相近的仿真分析模型,对基础变形模拟过程进行了仿真分析,与实测结果进行对比。建立模型中包含沉降板、围挡、立柱等边界条件,以及地基、无砟轨道等变形主体。模型中地基与围挡间设置可分离的接触边界,摩擦系数取为0.2,地基内中砂与细砂的回弹模量测试结果相差较小,分别取为25和15 MPa。所建立的模型如图18所示。
路基厚度0.5 m,最大实际沉降变形下,不同基础变形波长时地基内沉降变形云图如图19所示。
底层和顶层的变形曲线与实测变形曲线对比如图20所示。
仿真结果与测试结果对比表明,实测变形量与仿真分析所得计算曲线能够较好地重合,波长较短时,沉降传递至上层时量值衰减越明显,波长越长时,沉降峰值衰减越小。

图18 路基变形模拟试验验证模型

图19 路基变形模拟试验验证模型
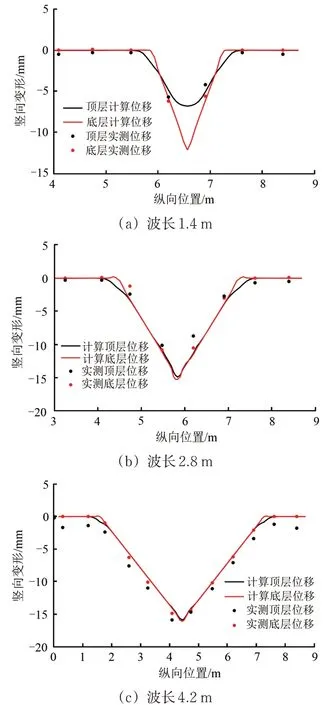
图20 测试结果与理论分析结果对比验证
5 结 论
(1)提出了无砟轨道—路基变形量纲相似模型设计准则:原型与模型尺寸比例为1:n时,材料弹性模量比例1:n、加载位移比例为1:n、重度γ比例为1:1、扣件刚度1:n2时,满足量纲相似准则,此时结构变形比例为1:n,应力比例为1:n。
(2)直接缩尺模型时,基础变形曲线吻合较好,但轨道板及底座板变形与实尺模型间差异较大,轨道板及底座应力分布也与实尺模型差异较大,无法直接推广至原型。采用相似模型时原型与模型的应力与变形基本一致,相似模型试验结果可直接推广至原型。
(3)在试验比选基础上,提出模型与原型比例为1:4的无砟轨道—路基变形相似模拟试验平台设计方案,采用中砂、细砂模拟路基材料,用掺膨润土砂浆模拟无砟轨道混凝土材料。通过底部节段变形板的设置实现不同变形波长的模拟,通过竖向调整装置实现沉降、上拱等不同路基变形量的模拟。
(4)依据本文提出方法搭建的试验平台实测变形曲线与仿真分析所得计算曲线能够较好地重合,验证了试验方法可靠性。初步试验表明,波长较短时,沉降传递至上层时峰值衰减越明显,波长越长时,沉降峰值衰减越小。
