高速磁浮列车隧道交会时洞内压力波动数值模拟研究

贾永兴，杨 振，姚拴宝，梅元贵

（1.兰州交通大学 甘肃省轨道交通力学应用工程实验室,甘肃 兰州,730070；2.中车青岛四方机车车辆股份有限公司 国家总成工程技术研究中心,山东 青岛,266111）

我国时速600 km 高速磁浮列车,规划试验速度达到650 km·h-1。德国常导磁浮列车TR—09载人最高试验速度曾达到550 km·h-1,日本超导磁浮MLX列车在山梨试验线的最高试验速度达到603 km·h-1。而世界上目前仅有的运营线——中国上海磁浮列车示范运营线运营速度为430 km·h-1。可见,相比于传统轮轨高速列车,高速磁浮列车的运营速度将显著提高,其空气动力学问题尤其隧道空气动力学问题势必更加突出［1］。按目前对轮轨高速列车隧道压力波问题的认识,2 列列车交会的隧道压力波问题更严峻。隧道压力波效应除引起司乘人员耳感不适问题和车辆车体及部件的疲劳损伤问题外,也会危及隧道内附属设备［2］及隧道内工作人员［3-4］。实际运营时,虽然可通过一定措施减小或避免隧道内交会,但在制定双线隧道净空面积等时则必须考虑隧道内交会工况。因此,有必要对高速磁浮列车隧道交会压力波问题进行研究。

然而,目前对高速磁浮列车隧道压力波问题的系统研究还相对较少,已公布成果多集中在日本、德国和中国。日本自1977年先后建成宮崎试验线和山梨试验线,对高速磁浮列车各类空气动力学问题进行了系统研究。菅沢正浩等［5］对MLX01试验列车的车体表面压力、车尾流动分离、气动阻力、微气压波及车内外噪声特性等进行了实车测试。山崎幹男等［6-7］结合实车试验及数值模拟方法,研究了3 辆编组MLX01 试验列车以500 km·h-1通过4 km 隧道时的压力波动。木川田一弥［8］采用浅水槽进行了试验研究,得出换算为实际车速500 km·h-1,阻塞比0.130 时,单列车在1 445 m隧道运行时隧道中央压力为9 kPa,交会时则高达18 kPa。近年来,高橋和也［9-10］、本田敦［11-12］以及齋藤実俊［13］等系统研究了浅支坑及开孔缓冲结构对高速磁浮隧道微压波的减缓作用。永長隆昭［14-15］等研究了高速磁浮列车通过隧道时的气动噪声问题。可见,日本学者的研究多集中于影响环境的微压波和气动噪声问题,这与日本高速磁浮线路采用74 m2隧道净空面积密不可分。

德国Emsland 磁浮试验线和我国上海磁浮列车示范运营线均没有隧道,对隧道压力波的研究相对较少。Monaco［16］等研究了磁浮列车明线交会时的压力波动和车体受到的瞬态气动载荷。目前可见的仅Tielkes［17］对传统ICE列车和磁浮列车的隧道空气动力学效应进行了对比分析,给出车外最大压力阈值为5.5 kPa时,对应300,350,400,450 km·h-1等级线路的隧道净空面积推荐值为72,95,123 和156 m2,并建议车体动态气密指数大于20 s。

上海磁浮列车示范运营线开通前后,我国学者以三维数值模拟方法对其空气动力学问题进行了探讨。张光鹏［18］等以单列TR 型磁浮列车通过隧道为研究背景,根据德国及ERRI 压力舒适度标准,对车速、隧道长度和气密指数等对隧道净空面积的影响进行了研究,列车最高运行速度设定为400 km·h-1。张兆杰［19］等对Fluent 进行了2 次开发,研究了250 km·h-1磁悬浮列车的隧道压力波问题。刘超群［20］等针对TR08常导磁悬浮列车,以150 m长隧道为界,分别对350,400和450 km·h-1条件下单双线隧道的内轮廓进行了比选分析。可见,限于当时我国上海磁浮列车示范运营线背景,相关研究速度多限定在450 km·h-1以内。

就研究方法而言,作为实车试验和模型试验的补充,近年来数值模拟方法的应用越来越广泛。针对隧道净空面积选取、司乘人员耳感舒适性等问题［21-22］,国内外学者基于一维流动模型,建立了单列车通过隧道与2 列列车隧道内交会压力波计算方法和专用程序［23-26］。而在研究隧道压力波形成机理及列车外形和辅助坑道等的影响［27-30］时则多采用三维数值模拟方法［31-32］。

本文基于一维可压缩非定常不等熵流动模型和广义黎曼变量特征线法,研究高速磁浮列车隧道内交会时洞内压力波动特性,以期为我国高速磁浮隧道内气动载荷评估及净空面积选取提供支持。

1 一维流动模型

高速磁浮列车隧道内交会时引起的压力波动问题在流动本质上与高速轮轨列车没有区别。高速磁浮列车通过隧道会引起伴随流动分离和传热的三维、非定常、可压缩湍流流动。但通常而言,隧道长度远大于其当量水力直径,除列车端部和隧道端口区域外,隧道内绝大部分区域内的流动可视为一维流动。

1.1 控制方程及数值模拟方法

以等截面且不设置竖井、斜井及横通道等辅助结构的无坡度高速磁浮铁路隧道为研究对象。首先做如下假设：空气与隧道壁面、列车壁面间的摩擦和传热等为不可逆因素；列车车辆绝对密封,即不考虑车厢内外空气交换；空气为理想气体。一维可压缩非定常不等熵流动模型的控制方程［26］如下。

连续性方程

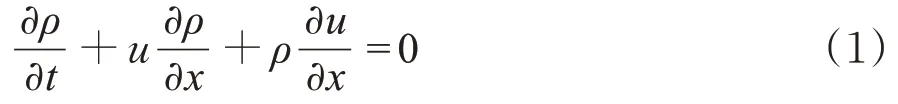
动量方程

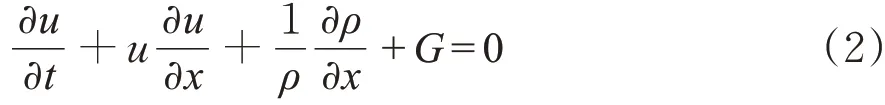
能量方程

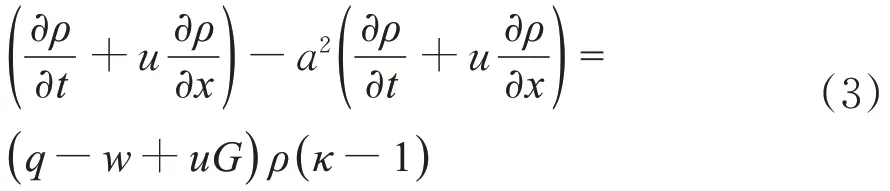
式中：u和a分别为气流速度和声速；ρ,p和κ分别为空气的密度、压力和比热比；t为时间,x为一维空间坐标；w,G和q分别为列车壁面对空气做的功、摩擦力项和空气与壁面间的传热项,详见文献［23,26］。

方程式（1）—式（3）构成的一阶拟线性双曲型偏微分方程组通常可采用特征线法［26］求解。除采用上述方程求解隧道内空气流动外,还需建立对应的边界条件描述隧道端口和列车运动端部的流动状态。对于隧道端口及处于单列车运行状态时的列车运动端部边界条件可采用一维准定常不等熵流动模型描述［26］；而隧道内2 列列车高速交会时,由于交会时间非常短,可忽略空气与壁面间的摩擦、传热等不可逆因素,采用不可压缩流动模型分别建立2 列列车头头交会、头尾交会和尾尾交会各瞬间的边界条件［26,33］。

1.2 模型验证

目前公开发表的高速磁浮列车隧道压力波实车试验结果的最高速度为500 km·h-1,但试验速度并非匀速。此处采用最高速度500 km·h-1日本旋成体动模型试验结果［25］验证本文一维流动模型的合理性。图1所示为距隧道入口2.35 m 处测点的静压时程曲线,可见2 条曲线完全吻合,说明本文计算方法可准确反映动模型通过隧道时引起的压力波动。计算得到的最大正压值和最大负压值与测试结果的误差分别为8.5%和1.8%。因文献［25］未明确给出试验相关的空气动力学系数,计算时只能采用估算系数,这可能是计算结果误差较大的原因。

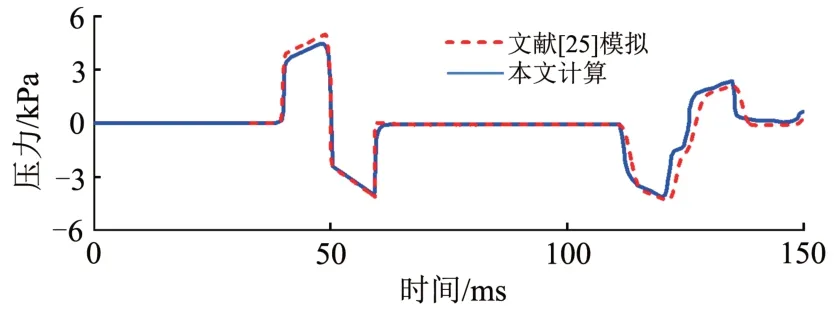
图1 距隧道入口2.35 m测点压力波动对比

验证结果表明,基于一维可压缩非定常不等熵流动模型及广义黎曼变量特征线法建立的计算方法和计算程序可准确预测隧道压力波变化规律,计算精度满足工程应用要求。需要说明的是,本节验证工况的动模型最高速度仅为500 km·h-1,而本文研究针对600 km·h-1等级高速磁浮列车,但两者对应的流动问题同属亚音速流动问题,本文建立的一维可压缩流动模型和求解算法完全适用。

2 隧道内压力波动峰值分布规律

隧道长600 m,净空面积为100 m2。高速磁浮列车为5 辆编组,运行速度为600 km·h-1。单列车通过隧道和2 列列车隧道中央等速交会（以下简称单列车通过和2列车交会）,隧道内距入口100 m处压力波动时间历程对比如图2所示。

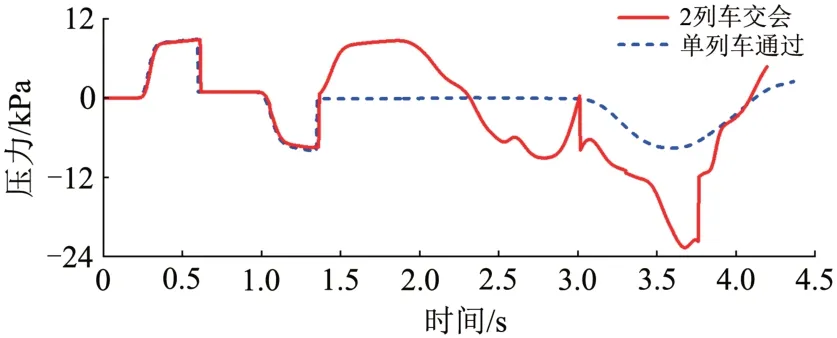
图2 隧道内距入口100 m处测点压力时程曲线对比

图3给出了单列车通过和2 列车交会时隧道内压缩波和膨胀波反射叠加图及列车运行轨迹线。图中黑色粗实线和粗虚线分别表示列车车头和车尾的运行轨迹线,容易发现,车头和车尾分别在0 s 和0.75 s 驶入隧道,在3.60 s 和4.35 s 驶出隧道。图中细实线表示压缩波,细虚线表示膨胀波,并以同一颜色区分各车头和车尾驶入和驶出隧道端口诱发的压缩波波系和膨胀波波系。以单列车车头驶入隧道入口诱发压缩波为例说明：车头驶入隧道诱发的压缩波以红色细实线表示,其在隧道出口端反射的膨胀波以红色细虚线表示,随后在隧道入口反射的压缩波再次以红色细实线表示。其余绿色、蓝色、粉色、橙色和青色线族类似,不再赘述。

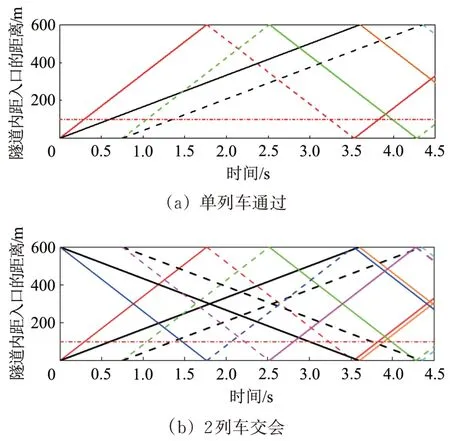
图3 压缩波、膨胀波传播反射及列车运行轨迹图

结合图2和图3可知：在0～1.47 s,即对向列车驶入隧道诱发的压缩波传播到距入口100 m测点前,2 列车交会时隧道内压力波动与单列车通过情形完全一致；t=1.47 s时,压缩波使得2列车交会时隧道测点压力急剧升高；t=3.0 s 时,对向列车车头通过地面测点,测点压力急剧降低；t=3.75 s 时,对向列车车尾通过地面测点,测点压力急剧升高。由此可知,2 列车交会时,对向列车诱发的压缩波和膨胀波以及列车通过均会影响隧道内测点的压力波动。

将“压力峰值”以最大正压、最大负压及压力峰峰值3个指标表征。单列车通过和2列车交会时,隧道内测点的压力峰值见表1。由表可知：2 列车交会与单列车通过相比,最大负压和压力峰峰值增幅显著；最大负压约为最大正压的2 倍；交会时隧道内最大负压接近-20 kPa,该结果也与日本学者木川田一弥［8］浅水槽试验结果吻合。相比于单列车通过,2 列车交会的最大负压增大约139.7%,而压力峰峰值增大约66.9%。

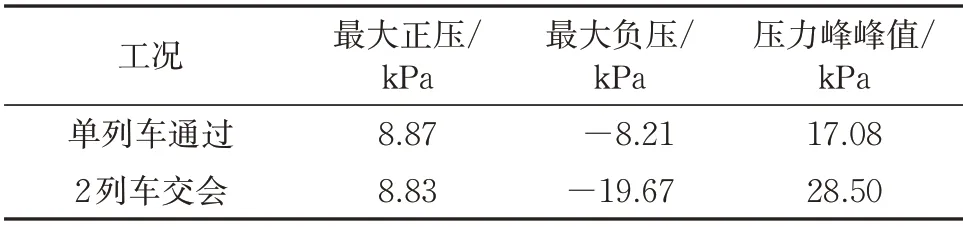
表1 隧道内距入口100 m测点压力峰值

高速磁浮列车为5 辆编组,列车运行速度取600 km·h-1,隧道净空面积100 m2,隧道长度取0.6,1.0,1.6 km,2 列车交会时隧道内测点压力峰值分布如图4所示。由图可知：2 列车交会时,隧道中央测点的压力波动最剧烈,压力峰值以隧道中央位置为中心点往两侧对称分布,曲线形状呈“纺锤”形,且隧道越长,“纺锤”的“扁平化”特征越显著。因此,下文均以隧道中央测点分析隧道压力波动特征影响因素。

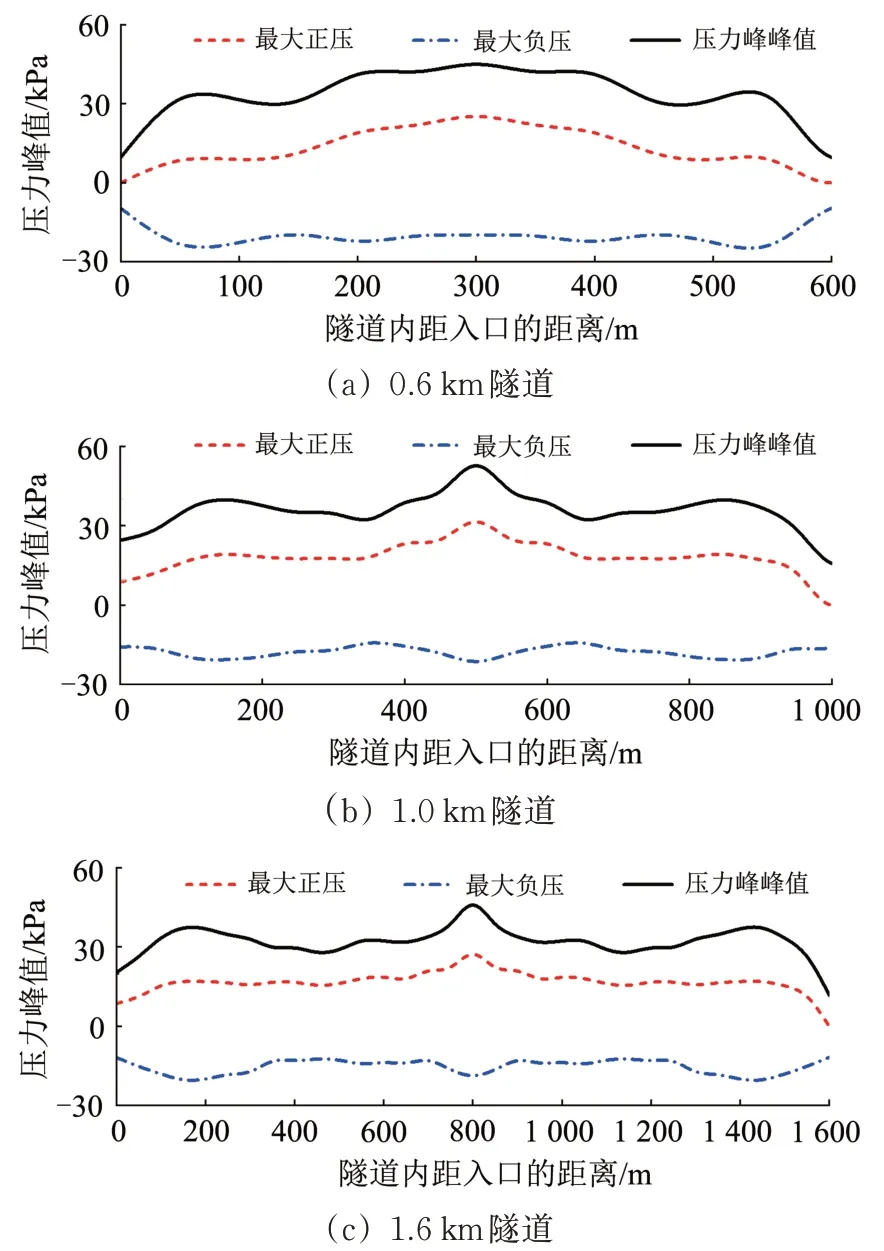
图4 等速中央交会时隧道内各点压力峰值分布特征

3 隧道内压力波动影响因素分析

3.1 隧道长度的影响

高速磁浮列车为5 辆编组,列车运行速度为600 km·h-1,隧道净空面积100 m2,隧道长度取300,320,340,...,800 m,计算不同隧道长度时2列车交会的隧道压力峰值,结果如图5所示。

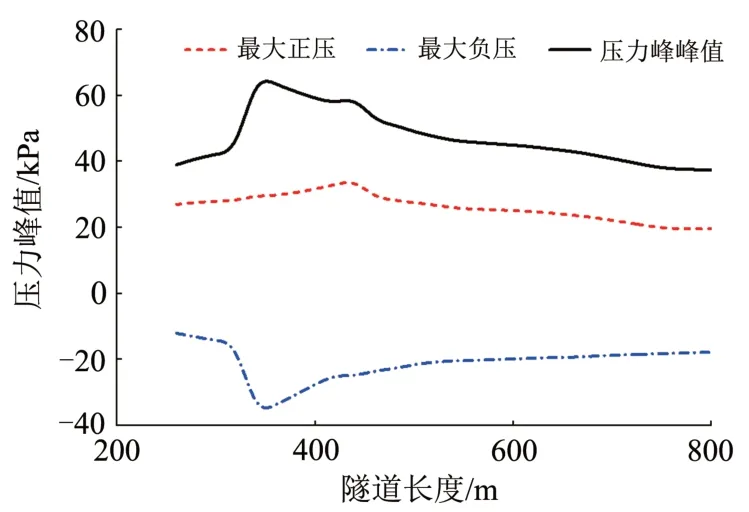
图5 隧道内压力峰值随隧道长度的变化曲线

从图5可以发现：随着隧道长度增加,隧道最大正压、最大负压和压力峰峰值均先增大后减小,说明存在最不利隧道长度；图中最大正压、最大负压和压力峰峰值对应的隧道长度分别为420,350,350 m。为确定覆盖工况范围更广的最不利隧道长度,进一步进行计算,列车运行速度取400 ～650 km·h-1,列车编组取3,5 和10 辆,2 列车交会时,基于隧道最大正压、最大负压的最不利隧道长度见表2,基于压力峰峰值的最不利隧道长度与基于最大负压的最不利隧道长度相同,不再重复列出。

由表2可知：最不利隧道长度与列车编组长度基本成正比,且列车运行速度在450 km·h-1以上时,最不利隧道长度有不断增大的趋势；列车运行速度为400～650 km·h-1、列车编组为3～10辆时,基于隧道内压力峰值的2 列车交会最不利隧道长度在160～1 000 m 范围内。以下研究均基于表2最不利隧道长度开展。

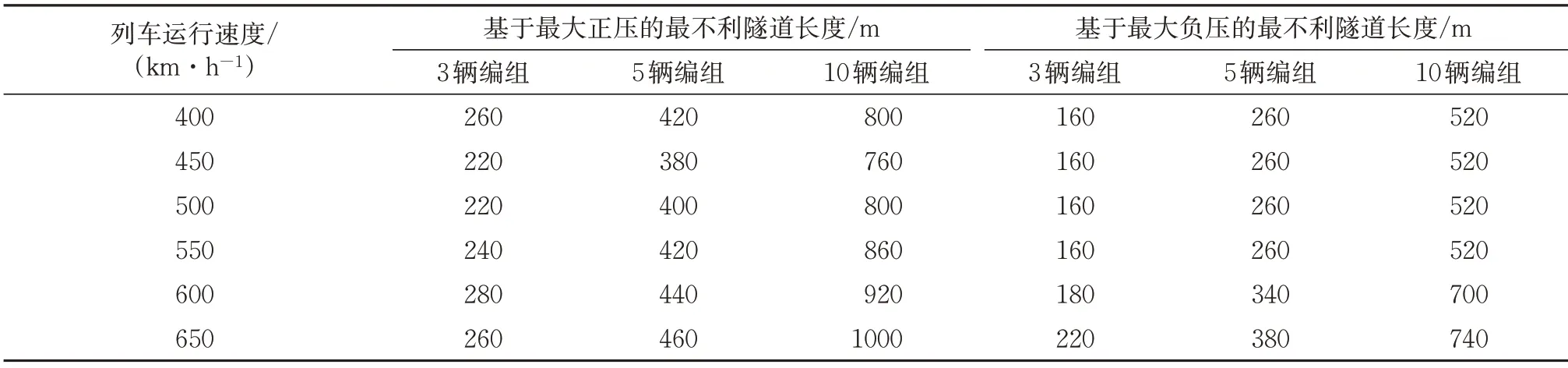
表2 基于隧道压力峰值的最不利隧道长度

3.2 隧道净空面积的影响

高速磁浮列车为5 辆编组,列车运行速度分别取400,450,500,550,600,650 km·h-1,隧道长度取表2中对应的最不利隧道长度,隧道净空面积取100,120,140,160,180,200,220,240,260 m2,计算不同隧道净空面积时2 列车交会的隧道压力峰值,结果如图6所示。

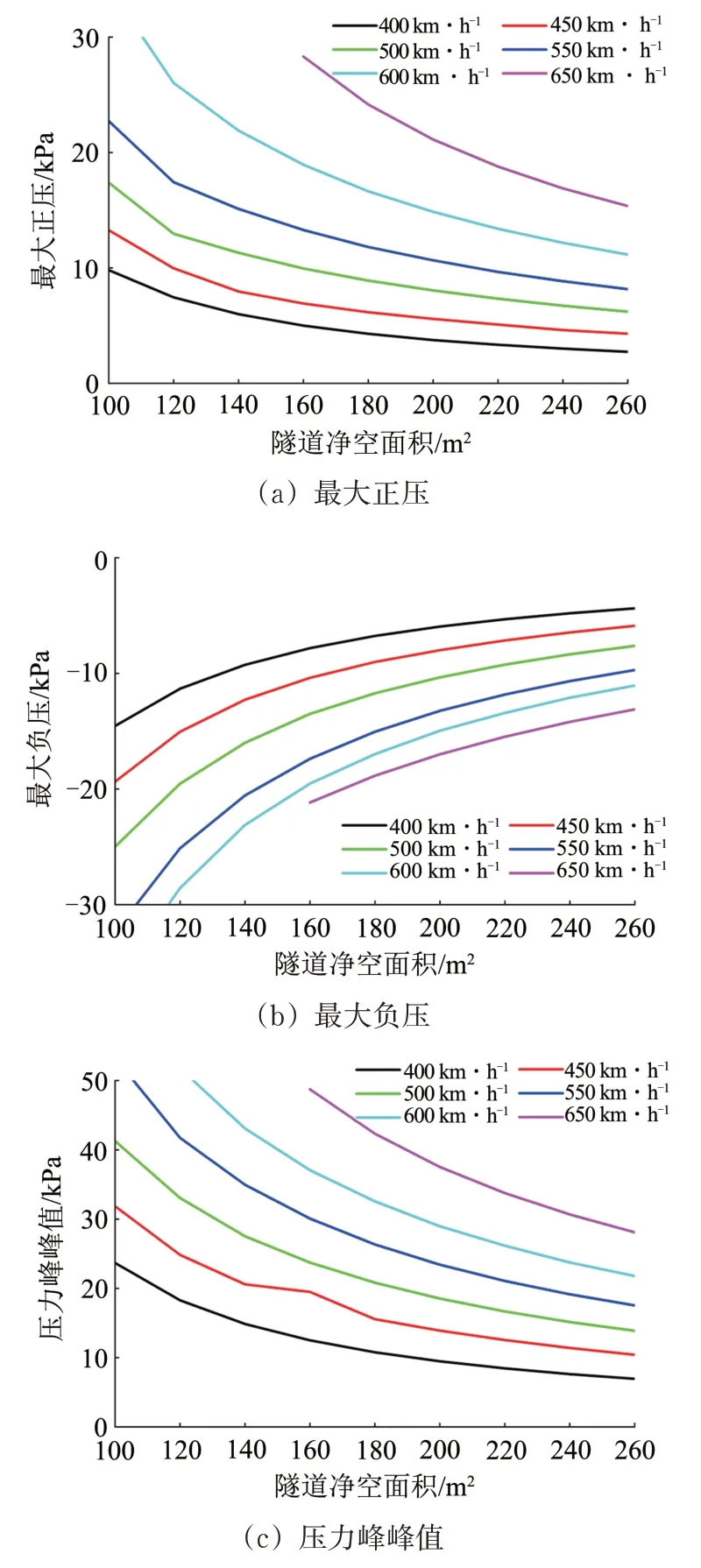
图6 隧道净空面积对隧道压力峰值的影响规律

从图6可知：隧道最大正压、最大负压及压力峰峰值均随着隧道净空面积的增大而减小,且列车运行速度越高,隧道净空面积增大对隧道内压力波动的减缓作用越显著；隧道净空面积为100 m2,列车运行速度为600 km·h-1时的最大压力波动峰值一度达到±30 kPa,对隧道衬砌和附属设施的气动载荷设计提出了更高要求。且该值明显超过ERRI医学健康标准中要求的任意时刻隧道内压力波动小于10 kPa 的要求。为满足ERRI 医学健康标准,必须增大隧道净空面积或增设竖井等减压设施。从图中反算也可得到：列车运行速度为600 km·h-1时隧道净空面积应不小于260 m2,400 km·h-1时隧道净空面积应不小于140 m2。

对图6工况下的数据进行拟合,得到不同列车运行速度时隧道压力峰值与隧道净空面积的幂次关系,幂次n的取值见表3。由表3可知：列车运行速度为400～650 km·h-1时,隧道最大正压、最大负压和压力峰峰值与隧道净空面积所成幂次n的取值范围依次为-1.1～-1.4,-1.3和-1.2 ～-1.3。

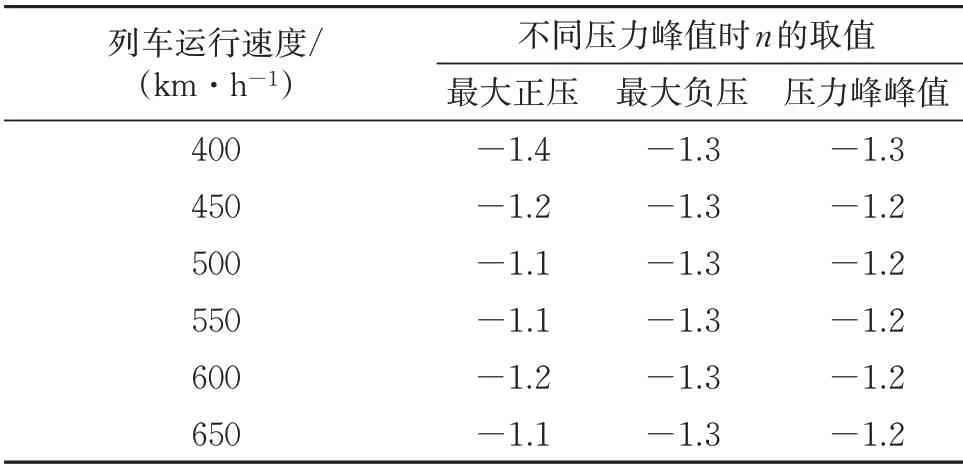
表3 不同列车运行速度时隧道压力峰值与隧道净空面积所成幂次n的取值

3.3 列车运行速度的影响

高速磁浮列车为5 辆编组,隧道净空面积取100,140,180,220,260 m2,隧道长度取表2中对应的最不利隧道长度,列车运行速度取400,450,500,550,600,650 km·h-1,计算不同列车运行速度时2 列车交会的隧道压力峰值,结果如图7所示。由图可知：隧道最大正压、最大负压及压力峰峰值均随着列车运行速度的增大而急剧增大。3 辆和10 辆编组时的变化规律与5 辆编组类似,这里不再列出。

对图7工况下的数据进行拟合,得到不同隧道净空面积时隧道压力峰值与列车运行速度的幂次关系,幂次m的取值见表4。由表可知：隧道净空面积为100～260 m2时,隧道最大正压、最大负压和压力峰峰值与列车运行速度所成幂次m的取值范围依次为2.7 ～3.8,2.0 ～2.3 和2.1 ～2.8。可见,相比隧道净空面积,列车运行速度对隧道交会压力波的影响更大。

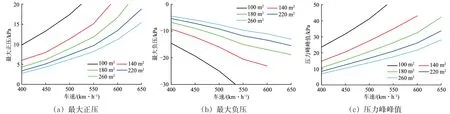
图7 列车运行速度对隧道压力峰值的影响规律

3.4 列车长度的影响

高速磁浮列车运行速度取600 km·h-1,隧道长度取表2中的最不利隧道长度,隧道净空面积取100,140,180,220,260 m2,计算列车长度为75,125,150,200,250 m（对应列车编组为3,5,6,8,10 辆）条件下2 列车中央交会时的隧道压力峰值,结果如图8所示。由图可知：随着列车长度的增大,最大正压有缓慢增大的趋势,最大负压和压力峰峰值均有缓慢减小的趋势,可认为3者均基本不随列车长度的增大而变化。

表4 不同列车运行速度时隧道压力峰值与列车运行速度所成幂次m的取值

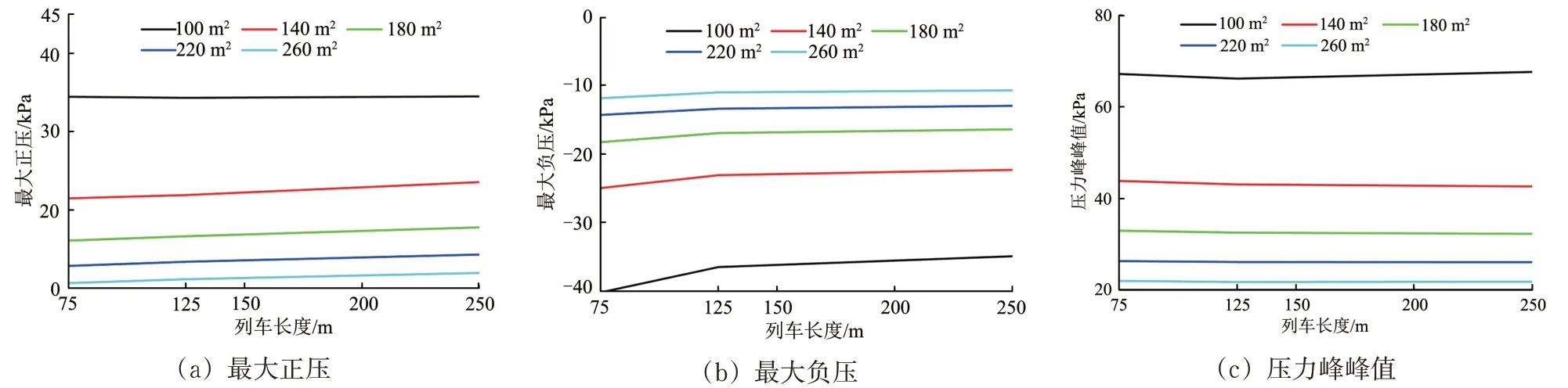
图8 列车长度对隧道压力峰值的影响规律

4 结 论

（1）2 列磁浮列车隧道中央等速交会时,相比单列车通过时最大负压和压力峰峰值均明显增大；隧道中央测点的压力波动最剧烈,压力峰值以隧道中央位置为中心点往隧道两侧对称分布,曲线形状均呈“纺锤”形,且隧道越长,“纺锤”的“扁平化”特征越显著。

（2）随着隧道长度的增加,隧道内压力峰值均先增大后减小。通过一维可压缩非定常不等熵流动模型和广义黎曼变量特征线法计算可知,列车运行速度为400～650 km·h-1、列车编组为3～10 辆时,基于隧道内压力峰值的2 列车交会最不利隧道长度在160 ～1 000 m范围。

（3）随着隧道净空面积的增加,隧道内压力峰值均减小；列车运行速度为400～650 km·h-1时,压力峰值与隧道净空面积的约-1.1～-1.4 次幂成正比。列车运行速度越高,隧道净空面积的影响越大,600 km·h-1时,100 m2隧道内压力峰值高达±30 kPa,为满足ERRI 医学健康标准,必须采用增大隧道净空面积或增设竖井等减压设施。

（4）随着列车运行速度的增大,隧道内压力峰值均急剧增大；隧道净空面积为100～260 m2时,压力峰值与列车运行速度的约2.0～3.8 次幂成正比。而列车长度对隧道内压力峰值几乎无影响。