牛顿、莱布尼兹究竟是如何“通过(看似)肯定不正确的数学途径得出正确结果”的——兼论对微积分核心概念的全新理解

(《区域供热》杂志编辑部，北京 100086)

本文标题中引号内的部分，为对微积分素有研究的马克思的原话，唯有括号中的“看似”两字为笔者所加。既然能够得到“正确结果”，其求解途径就应该是正确的，之所以通常被认为是不正确的，只是它被隐藏在了被无意中省略了的求解步骤之中了。这个问题，笔者自认在参考文献中所列论文中已经彻底解决并阐述的非常充分了，读者自可解之。在本文中，笔者愿对相关问题再做些精炼、明晰的表述，以就教于识者。

一、牛顿、莱布尼兹的求导过程本质剖析

众所周知，“第一代微积分”(牛顿、莱布尼兹)虽求出了导数，但却会产生“贝克莱悖论”(习惯称谓，实际是“佯谬”)，从而引发所谓历史上的“第二次数学危机”。以最简单的二次函数y=x2为例(本文为节省篇幅及使问题更直观以利于读者理解，不失一般性，均以二次函数为例讨论，不再做一般函数的抽象表述)，我们有求导过程

(1)

当公式中的Δx=0时，等式最左边得0/0，等式最右边得精确的导数2x，显然矛盾，即所谓“贝克莱悖论(佯谬)”。但是，无可否认的事实是，牛顿、莱布尼兹确实又是非常精确地求出了Δx=0点的导数值2x，而“无须那些无限接近却永不可达的昏话”(马克思语)。那么，牛顿和莱布尼兹究竟是怎么能做到这点的？未见后人予以澄清。事实上，请看公式1。我们问：由公式1中的Δy/Δx=(2x+Δx)Δx/Δx，如何得到导数的准确结果2x的？公式中的三个Δx，同时等于0可以吗？当然不可以，因为此时它显然等于0/0。等于非0的任何数，哪怕是无穷小，可以吗？当然也不行。唯一的可能，就是式子中的Δx/Δx=1/1=1，而式中2x+Δx中的那个Δx=0才可能得到最终结果2x。换言之，(2x+Δx)Δx/Δx中的三个Δx绝对不能同值。既然如此，式中的Δx/Δx就应该写成Δx1/Δx1以示与2x+Δx中的那个Δx相区别，而不能再写成Δx/Δx。即原先的Δy/Δx=(2x+Δx)Δx/Δx，必须写成Δy1/Δx1=(2x+Δx)Δx1/Δx1，当其中的Δx1=1，Δx=0时，才能最终得到准确并且唯一的结果(2x+0)1/1=2x。舍此而外，我们没有任何其它途径能够得到它。而我们所熟悉的Δy/Δx=(2x+Δx)Δx/Δx，显然是作为非线性的二次曲线函数的增量比值函数，Δx为其自变量，式中的三个Δx必须取相同的值。当然，也可以看成是该二次曲线与其割线的两个交点的纵、横坐标差之比，见图1。

显然，由于比值函数分母上有自变量Δx，因此Δx≠0，得不到想要得到的那个2x。而Δx=0，必有0/0，也不行；但新得到的Δy1/Δx1=(2x+Δx)Δx1/Δx1呢？它其实是线性的、该二次曲线的割线的增量比值函数，Δx1是其自变量，见图2。

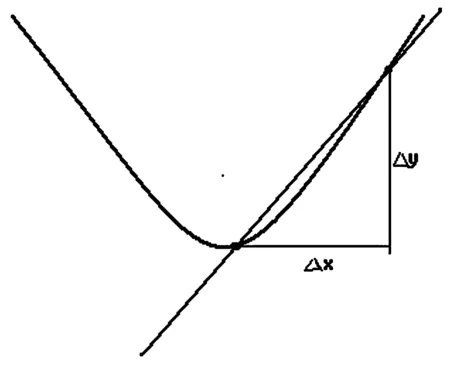
图1图中自变量Δx只依赖于曲线上的二点，不能离开曲线，Δx=0时不能作为分母

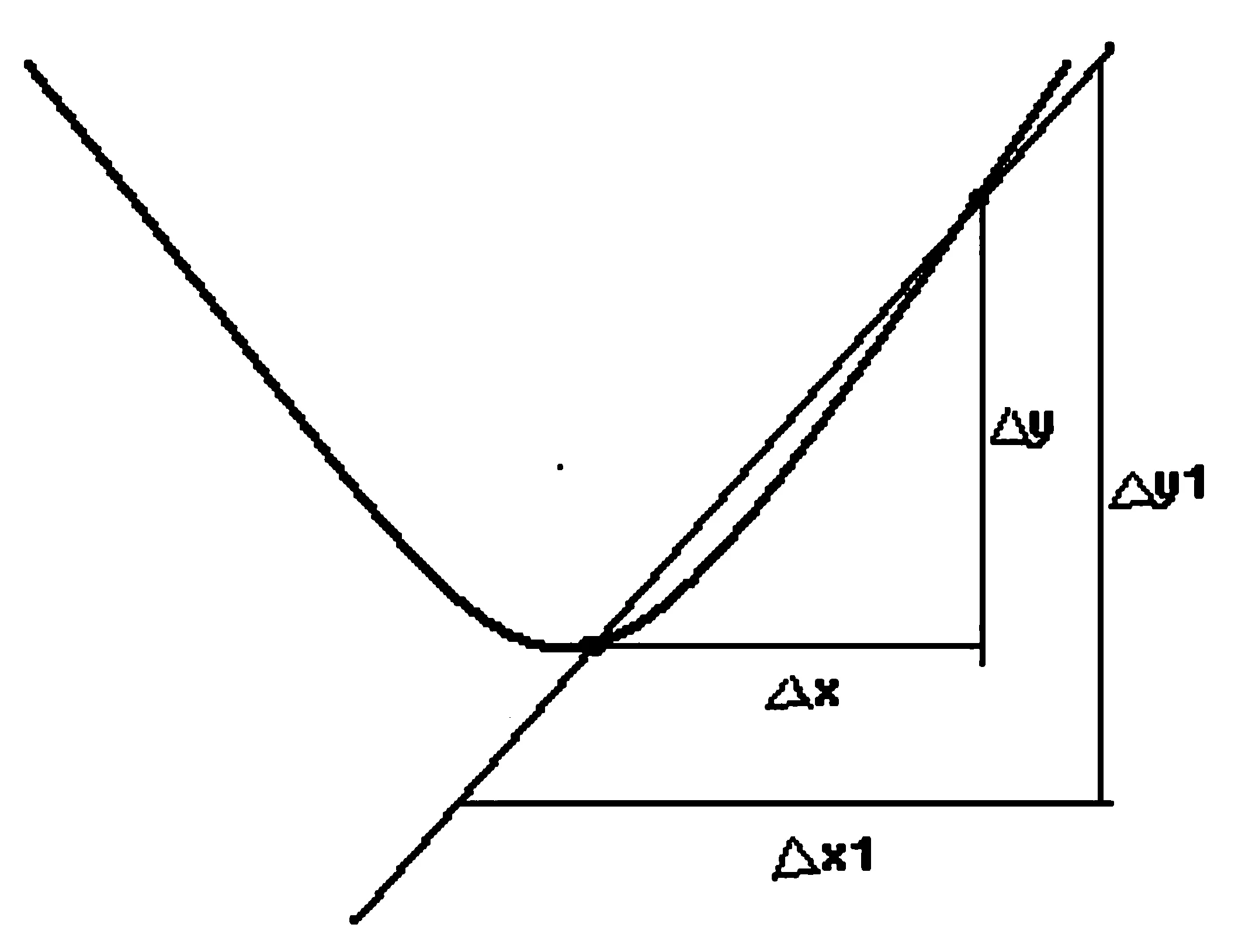
图2图中Δx1、Δy1可以脱离曲线，只在直线(割线)上，可为分母，因为其不能为0.

显然，作为线性函数二次曲线的割线函数与其增量对应的直线上两个点并不依赖于该割线与二次曲线的交点，它们可以是割线上的任何位置的两个非重合的点，因此显然当Δx=0时，割线变成切线，再取Δx1=1，自然得到2x，见图3。

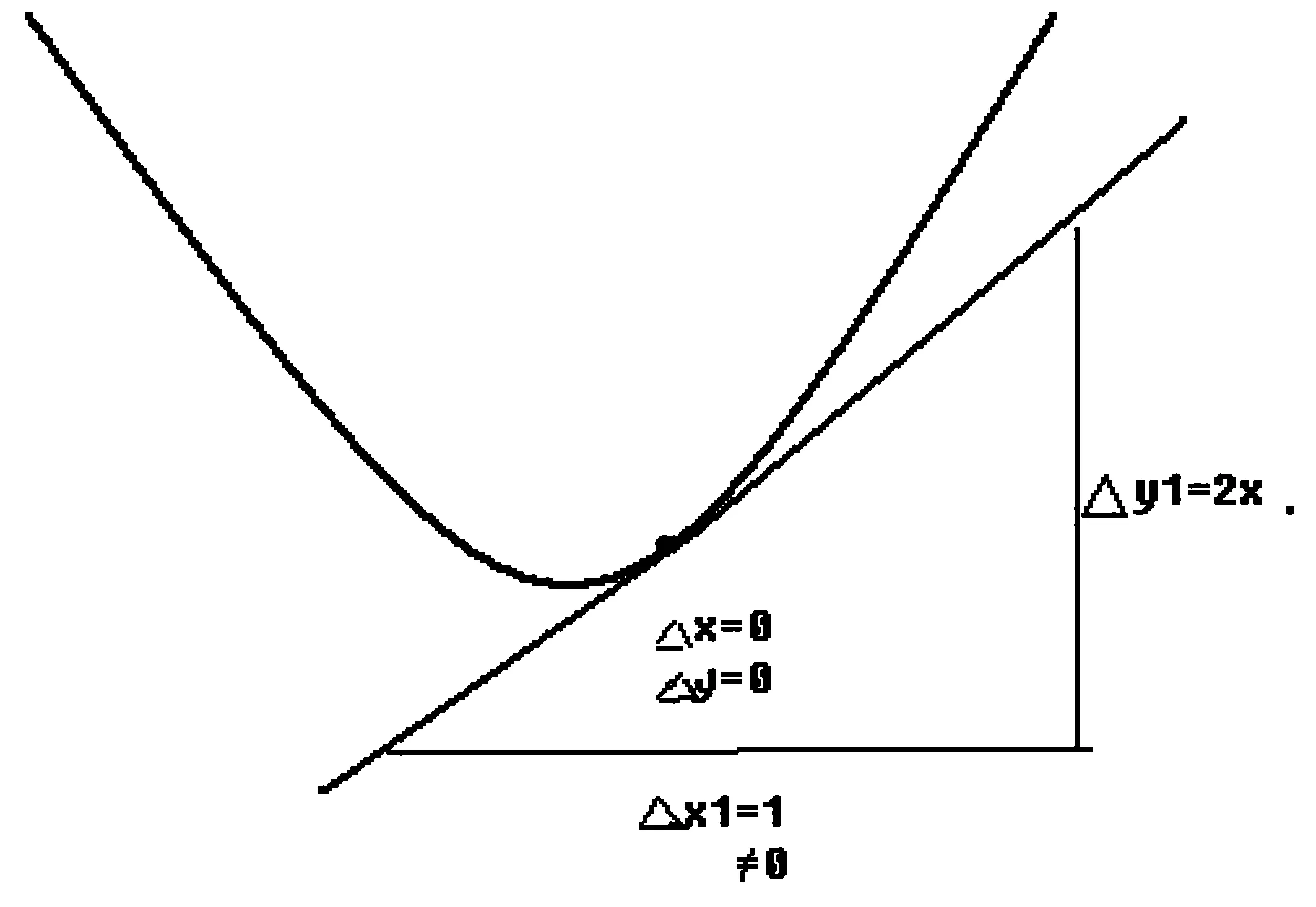
图3

当然，式中Δx1可以等于非0的任何值，因为比如2/2、3/3等，数值上都等于1/1=1，也就是都可以最终“折合”成1/1。因此在Δx≠0时，Δx1可以(当然不是“必须”)等于Δx。但当Δx=0时，必然有Δx≠Δx1，因为Δx不在分母上因此可以等于0，而Δx1由于处于分母而不能等于0。同时显然，只要令K(Δx)=2x+Δx，我们就可以有Δy1/Δx1=(2x+Δx)Δx1/Δx1=K(Δx)Δx1/Δx1，其中这个K(Δx)就是这个二次曲线的割线的斜率。它也是二次曲线的增量函数的自变量Δx的函数，当Δx≠0时，是割线；当Δx=0时，是切线。它只与该直线的斜率有关，与该直线的自变量增量Δx1全然无关。而当Δx1作为比值函数的分母时，它当然不能等于0(实际值是等于1)，否则会得到无意义的0/0。因此，Δy1/Δx1才是真正意义的切线斜率，也就是几何意义的导数。可以看出，这里分母不是0，也不必是无穷小(即使是，也要折合成1)，更不是传统意义上的趋于0的极限。总之，导数概念无涉无穷小或极限，它就是两个宏观量的比值。其可以兼容无穷小，但不是必须如此。物理意义的导数，最常涉及的是瞬时速度。参考前述导数的几何意义，我们可以得到全新的瞬时速度定义：一个原本在外力作用下做加速或曲线运动的物体，当所有外力在某瞬时突然解除，此时及其以后该物体所做匀速直线运动的速度。而匀速运动本身按这个定义，它没有受到外力，因此其瞬时速度与平均速度是一致的。可以看出，这个瞬时速度的定义与传统定义是完全不同的。按传统定义，曲线或变速运动，再小也不是直线匀速运动，无穷小也不行。除非是一个近似，但这会有误差。如果是极限，则瞬时速度不能表示成一个比式，也不能有量纲，实际上也不行。

最后，必须明确一点：的确，许多教科书都有“导数就是切线斜率”这句话。但如真的如此，为什么不采用笔者上面及系列论文中提出的这个最为直接、准确、明快的方法或诠释，而非要舍近求远地用远非直观的极限法来求导？况且按直线斜率的定义，它必然是个比式(分式)，因此无论有没有分母(所谓“没有分母”，实际也是分母为1)，也绝对不能是分母为0。事实上，稍微细致或严格一点的教科书，都会提到：经由极限法“求出”的导数，不能是个分式(否则分母只能是0)而只能作为一个抽象的“整体”看待，分子分母即使写上了，如dy/dx，dy及dx也不能分离、移项，像一个真正的分式那样去运算。因此，它仅仅是在数值上与切线斜率相等而已，而绝对不可能是真正的、完整意义的“切线斜率”，除非按本文提出观点来解释。

上面对微积分求导过程的诠释，实际正是牛顿、莱布尼兹当年的求导过程。因为公式1最后一步，实际是“消去”了分母上的自变量Δx(作为必要条件)后才令原式分子上的2x+Δx中的Δx=0的。可“消去”的定义是：“对代数式，只能通过约分的方式，才能消去分母”(百度)。而“约分”的定义是：约去公因数化为最简分式(或“把分式化为最简分式的过程”)。其方法是：根据分数的基本性质“分数的分子和分母同时除以一个相同的数(0除外)，分式的大小不变”来约分(见百度)。特别注意，按这些定义，约分后最终应该还是一个分式，只不过“最简”了而已。因此显然，严格意义上即使分母全部是公因数而被“约去”等于1了，这个最终的式子仍然是一个分式，只不过其分母已经“最简”到了“1”也罢。这是对约分定义的严格解读后只能得出的结论。因此可以明显看出，所谓“消去分母”，不过就是通过约分运算把分母化为1后，再舍弃(不写)这个1而已。因为数值相等，作为一种书写的简化一般情况下这是可以的(指不去再写这个分母上的1)，但是，在逻辑上，或次序上，显然是首先通过对分式的约分得到分母为1的一个分式后，才可以考虑究竟消不消去这个分母上的1(严格说是整个分式中的“1/1”)的。可是，一个将分母化成1的约分操作，不就是等价于使得分母等于或趋于1(以1为极限)的一个操作吗？二者是完全等价的。因此，令分母以1为极限或求得这个极限1的操作，在逻辑上是先于消去分母操作(也就是不再写分母上的这个“1”)的，如此，还怎么能说对逻辑上“在后的”消去分母上的1把一个分式变成非分式之后的式子，所求得的一个与分母已经毫无关系的、特别是自变量趋于0的极限，就是逻辑上“在先的”原分式分母趋于0的极限操作呢？这叫本末倒置：通过在先的约分，已经等价地令分母为1或趋于1或极限为1了，哪里还有这个分母趋于0的事？如果再趋于0，也是另一个函数也就是非比式(分式)函数的极限，而绝对不会再是原比式(求导所要求的)函数分母趋于0的极限。也就是公式2中的不等号成立，而等号不成立。这是因为对(2x+Δx)Δx/Δx分子分母的约分，按定义实际是在前式中分子分母各除以一个Δx，即[(2x+Δx)Δx÷Δx]/(Δx÷Δx)=(2x+Δx)·1/1。尽管这个最简分式的分母为1了，但严格而言它仍旧是一个分式。直接写成2x+Δx在大部分情况下是可以的，但对一个涉及分母的求导(求极限)过程是不行的。更何况早就有说法“任何除0外的整数都可以看成分母为1的假分数”(百度)。

此外，对Δx/Δx这样的自函数，几乎所有人及教科书都说，由于在任何Δx≠0的点，该函数都等于1，因此在Δx→0时，其极限只能是1，尽管在0点此函数无有意义的函数值(函数值为0/0)也罢。只不过这个结论只有在“消去分母上的自变量Δx”进而先要对分子分母进行约分后才有可能。但即使对一个最简单的自函数的增量比值函数Δx/Δx而言，对其约分也意味着要严格按约分定义有(Δx÷Δx)/(Δx÷Δx)=1/1，这当然就是分子分母中的Δx=1或Δx→1，绝对不是Δx→0。至于由约分得到的1/1再“消去”分母上的1后，这个“1”在Δx→0时仍旧等于1，那是另外一个函数的事了。它无论在逻辑上、运算上，都不是原先要求的Δx/Δx直接令Δx→0得到的极限值。总之，前面教科书中的“只要Δx不为0，就等于1”云云，实质就是等价于Δx→1或Δx=1，此“运算”逻辑上是在Δx→0之前的。它“隐含”在了约分这个操作之中，为前人所未察而已。用物理上的速度概念来理解，更其简单。此时自函数的增量比Δx/Δx的分母为时段，分子为走过的路程。当时段等于1或趋于1时，整个比式1/1表示的当然就是“单位时段所走过的路程”，也就是“速度”。而按前文笔者对瞬时速度的定义，对匀速直线运动而言，瞬时速度与平均速度不仅是等值的，而且就是一回事。完全无需“多此一举”地再去求那个分母趋于0的不可达极限。不要说这个极限根本就没有(前文)，就算有，那个瞬时或时间点居然不可达，怎么解释？现实中任何瞬时或时间点，不都是到达了的吗？这简直就是芝诺悖论的翻版，极限法求导的所谓“标准分析”或“第二代微积分”，本质上就是试图以芝诺悖论的方式求导或给导数以解释，有人却还反过来说极限法微积分解决了芝诺悖论，这说法本身其实就是一个悖论。此外，按极限运算规则，当Δx→0时，Δx/Δx不能等于0/0，但其理由正是当Δx→0时Δx/Δx得到了0/0，而按规则分母不能为0。因此不允许以0/0为极限(严格讲0/0不是“有意义的极限”)。这里有一个逻辑先后问题：0/0没有出现，怎么知道得到它的极限不被允许？或许还可以从另一个角度看：1/Δx的分母Δx是无法与分子上的那个“1”相互消去的。其在Δx→0时的极限是什么？1/0，一种认为不允许，一种认为是无穷大∞。但无论哪种看法，都不会有二者经过与其它数的运算得到1的情况出现。于是，由Δx/Δx=Δx·(1/Δx)，按极限规则“积的极限等于极限的积”，Δx/Δx在Δx→0的极限等于Δx→0的极限乘以1/Δx的Δx→0时的极限，即有0·(1/0)=0·∞=0/0，无论如何解释这些结果，反正与1无关。

再看微分问题。通常教科书中首先定义微分为函数的线性部分(通常为“线性主部”，但有时并不尽然。见齐民友《重温微积分》)。然后再由此就有了自变量的微分等于其增量dx=Δx及其所引发的问题。显然，自变量也是函数，起码是可以成为函数。况且孰为自变量，孰为因变量，其地位是平等的。因此，产生了两个不同的微分定义共存于同一系统甚至同一变量的问题(国内先后由师教民、莫绍揆、梁赞臣、丁小平等指出):一个是增量的线性部分(通常为dy)，一个是增量本身(通常为dx)。但出人意料，作为第二代微积分的创建者之一的柯西，却并不是这么做的。他首先由极限法给出并定义了导数f’(x)，然后“通过把dx定义为任一有限量而把dy定义为f’(x)dx”。显然，这里定义自变量的增量dx逻辑上在先，而定义函数的微分也就是“线性部分”的dy逻辑上在后。表面上，两种定义方式似乎没有什么大不同，但这是以往的认识。柯西的定义方式，并没有提函数增量Δy本身，尽管dy实际就是函数增量Δy的线性部分。但柯西没有以与函数的关系来定义dy。而且也没有说它就是微分，它显然也是个有限量。如此，前述自变量的dx=Δx问题本不存在。柯西这里的dy、dx，就是本文前面的Δy1、Δx1，也就是切线斜率的纵、横坐标的增量，并且十分明确地，它们都是有限量(宏观量)，而不是无穷小或极限。二者的比值，即这里的dy/dx，当然就是前文的Δy1/Δx1，当然就是导数值。那么，问题来了：既然如此，何不就直接把导数f’(x)定义成有两个有限量的比dy/dx(即Δy1/Δx1)？一如笔者在本文中所做的。因此，用极限求导(“标准分析”、“第二代微积分”的做法)，且先不论对错，根本就是没必要的。柯西的做法，实际已经很接近真相了，就差这么半步。柯西(如果没有理解错的话)还指出，微分作为一个辅助概念，在逻辑上没有也行。后世教科书之所以紧抓住“函数的线性主部”不放，显然是意识到不如此，就没有了趋于极限时的、或达到无穷小时的“曲化直”。更何况此二者无论哪种解释，都是有问题的(会使贝克莱悖论在积分时重现。见笔者系列论文)。但按笔者无论对导数还是积分的解释，就不会再有这类会产生矛盾的问题。细节这里就不赘述了，有兴趣的读者大可看参考文献中笔者的系列论文。

总之，牛顿、莱布尼兹当年已经实际地求出导数的精确值了，但始终没有给出一个简单、明快、无矛盾的诠释。他们(包括后来的极限法求导，即所谓第二代微积分或标准分析)很随意地就“消去”了分式中的作为自变量的分母，但是没有理会、搞清、回答这个消去分母究竟意味着什么？笔者的回答很简单：严格按定义，那就是“意味着在分式值不变时把分母值折合为1”(当然在大部分情况下这个1可以不写，这就是“消去”)。但求导问题不能不写。这就是贝克莱悖论(实际是“佯谬”，绝对不是逻辑学意义的“悖论”)之所以产生的根本原因。也就是说，不写这个分母1，就会有悖论(佯谬)；写了，就没有。马克思说：微积分是由一个明显错误的过程，得到完全正确的结论。如果说有错误，那这个“错误”是什么？说来简单，就是没有写这个本应该有的“分母1”。一旦把这个1写在分母上，自变量不是等于1就是趋于1(Δx=1或Δx→1)，根本不会再有等于0或趋于0(Δx=0或Δx→0)的问题，也就不会再有任何马克思所说的“错误”了。总之，牛顿、莱布尼兹在求导过程中的实际做法是完全正确的，唯一遗憾的是没有意识到分母上在做了“约分”操作后还应该写上一个“1”。因此他们在求导过程及导数的定义上出现问题。也就是求出了正确、精确的结果，但没有给出一个正确、合理的解释。实际上，如果最初就将整个求导过程交付给计算机程序，令其严格按各个概念的定义，当然特别地包括约分定义来操作，当不至于出此疏漏以导致贝克莱悖论(佯谬)的发生。不得不说，在此问题上，机器可以再一次轻松地战胜很多人。

此外，这里做一个说明。此前笔者的论文中，都是说的“由除法使得分母折合成1”等等。虽然除法、约分、消去分母等等说法大同小异，几乎可以互代(起码在绝大多数情况下)，但严格讲仍有一定的差别。这个前文已述了。比如除法的定义是：已知两个因数的积与其中的一个因数，求另一个因数的运算。这里并没有分母为1和量纲。只有在分式的约分中才有这些概念。因此为更加的严格化，宜以本文中的更为有力、明确的说法为准。即由除法得到的分母可以写1，应该写1(以往论文说法)，到由对分式的约分得到的分母必须写1(本文说法)，区别仅此。

退一步讲，如所周知，之所以需要极限法第二代微积分，是第一代微积分产生了贝克莱悖论。否则第二代微积分便没有必要存在。但正因为会产生悖论(矛盾)，第一代微积分理应就是错的(任何产生矛盾的系统都是错的)，所以才会有用“正确的”第二代微积分取代它的必要。那么既然第一代微积分是错的，它本应根本求不出、或求出的是错的导数。可是，第一代微积分明明求出了正确且精确的导数。否则微积分的发明权就应该被授予柯西、外尔斯特拉斯等人，而不是牛顿和莱布尼兹。总之，极限法的第二代微积分如对，它所要取代的第一代的牛顿、莱布尼兹微积分就是错的。既然错，它所求出的导数就应该是错的。但事实是对的。也就是，极限法即使是对的，它也仅仅是表明自己求出了正确的导数，而且不会再产生贝克莱悖论，它其实并没有解释为什么第一代微积分可以在贝克莱悖论存在的情况下也能求出正确的导数，而不是求不出导数或求出的是一个错误的导数。总之，第二代微积分充其量只能做到“独善其身”，它指不出第一代微积分究竟错在何处。明确说，就是指不出第一代微积分究竟何以会产生贝克莱悖论。如果说正确的第二代微积分取代了错误的第一代微积分理论，但为什么它得到的导数值不过与第一代所得到的完全一样？总之，无论是正确的与错误的一致，还是错误的与正确的一致，逻辑上行得通吗？

二、极限法微积分(第二代微积分、标准分析)求导中的逻辑问题的另一角度分析

第二代微积分所涉及的极限，当然指的是“不可达极限”，也就是在极限点未定义函数值，但可以有极限值。比如设有自函数x(x≠0)，其在0点无定义，但却可以有极限值0(当x→0时)。但还有另一种情况，极限法微积分显然认为也是成立的，这就是在某点虽没有有意义的函数值，但却可以有有意义的极限值。比如自比函数x/x，在x=0点的函数值为0/0，无意义，但极限法微积分却认为其x→0的极限值为1。这显然是分子分母上的两个x先相消得到1，此时x再趋于0，此时“1”已然与x无关，它还是1，遂认为极限为1。显然，极限法并未严格区分这两种情况，认为它们是一回事，但事实果真如此吗？

仍以简单的二次函数为例，极限法求导的过程如公式2中左数第一个等号右边开始(先不要去理会最左边的那个“0/0”，它是为以后的讨论预先写下的；也先不要理会式中那个不等号：权且就当其为等号)：

(2)

其关键步骤仍旧是公式2中不等号(先就认为是等号)两边显示的那个“消去”分母上的自变量Δx。通常，人们给出能够这么做的理由是：既然函数在Δx=0点无定义，那么，只要不在该点，分母就不会等于0，也就可以消去分母上的那个自变量Δx，然后再令已经没有分母Δx的2x+Δx(原先分式中分子的一部分)中的Δx→0，即可得到导数2x了。但这种逻辑以往看似天衣无缝，其问题在本文第一节已经讨论的很充分了。同时，从另一视角，其也经不住如下的诘难和推敲：

极限法的第二代微积分求导成立的充分必要条件，显然是公式2的推导过程只能是从左至右方向进行。因为不对公式2进行从左至右的推导，原始公式中的分母上的自变量Δx就无法“被消失”(正规叫“消去”)，以下一切结论就都得不到了。但公式2中的各式既然以等号(先不理会那个不等号，就认为该位置为等号)相连，显然是相等的或起码被认为是相等的。既然如此，推导顺序为什么只能是唯一地以消去分母上的Δx为目的的从左至右？为什么不可以反过来，从右至左推导？具体说就是，公式2成立的基础，是在条件Δx≠0的前提下，(2x+Δx)Δx/Δx=2x+Δx等式成立(反之在Δx=0时，等式不成立，一个函数为0/0，一个为2x)。但正因为等式成立，就不存在在Δx≠0的前提下，只能消去该等号左边的(2x+Δx)Δx/Δx分母上的Δx得到2x+Δx，而不能在在同样的Δx≠0的前提下，在该等号右边的2x+Δx加上一个分母Δx(实际是乘以Δx/Δx)而得到(2x+Δx)Δx/Δx的问题。在Δx≠0的前提下，尽管函数值在上述等式二边相等，但并未明确在Δx=0时等式二边的极限值也相等，因为此时这个极限值已经在函数的定义域Δx≠0之外，而在Δx=0点，两个函数的函数值一个为0/0，一个为2x，完全不一样。也就是说，公式2从左至右地推导，在消去分母Δx之后(必要条件)，才可得到那个2x。那么既然如此，同样的公式2，从右至左地推导，乘上一个Δx/Δx(反正此时分母Δx≠0)，不就得到极限值0/0了(尽管是无意义的)？起码此时是得不到把消去分母作为必要条件的2x的。因此在得出二者在Δx=0点的极限值一样为2x而违反函数值不一样的结论前，需要给出明确的证明，否则就是使用了未经证明的命题。但显然这个证明是给不出的：因为同样的理由，也可以有0/0为二者的极限值，因此2x为二者的极限是不成立的。也就是根本就没有这样的逻辑：在Δx≠0时函数值相等的二函数，其在Δx=0点的极限值必相等。特别地还必须等于2x。而极限法求导的第二代微积分也就是从左至右的公式2推理过程，必须要有此一条实际并不存在的原则才行。因此，如欲(2x+Δx)Δx/Δx与2x+Δx的极限值相等，除了条件Δx≠0外，还要有条件Δx不能趋于0。或者必须首先证明当Δx→0时，(2x+Δx)Δx/Δx的极限不是0/0，而且这个证明不能是在消去分母上的Δx后给出的，否则这就是逻辑上的“循环论证”。因此，极限法之误，是把在某条件(Δx≠0)下的事实(函数值相等)，误认为在加进了新条件时(取Δx→0时的极限)就相等了。总之，如果我们先有函数2x+Δx(Δx≠0，注意，在Δx=0点无定义或“不去”进行定义)，其在Δx→0的不可达极限当然是2x(与在Δx=0点有定义的2x+Δx在该点的函数值相等)。而此时这个2x+Δx既然有了条件Δx≠0，按前述从左至右推导的同样原则，那利用乘以一个分式Δx/Δx(在Δx≠0时其数值不是恒等于1吗？)在其分母上加一个Δx又何妨？具体就是在Δx≠0的条件下，从2x+Δx得到(2x+Δx)Δx/Δx。如此，再令Δx→0，求得极限值也为与其函数值一样的、公式2的最左边的0/0(尽管其并非有意义的也罢)。难道我们能够就此得出结论：在限制条件Δx=0点无定义(即定义域为Δx≠0)的2x+Δx在Δx→0时的极限值不是2x而是0/0？可见，说一个函数在Δx=0无定义就可以随意消去或加上分母上的自变量Δx以求得其极限的做法都是错的，会产生矛盾。换言之，可以消去分母上的自变量Δx的前提(充分必要条件)，不但像通常被公认的要求在Δx=0点不能定义函数值(因该点的函数值首先应是0/0，然后才有的该函数的定义域不能包括Δx=0点这个结果。前者是后者之因)，其实在该点同样也不能定义极限值(因该点的极限值也是0/0，与函数值一样。有人也许会武断地说，“没有极限0/0”，但这句话本身里面已经有“极限0/0”了。因此此句话自相矛盾，类似谎者悖论。实际的表述应该是先有极限0/0，然后才得到它“不是有意义的极限”的结论。因果关系要明确)。也就是说，如果仅仅把函数的定义域不包括Δx=0点作为可以消去分母上的自变量Δx的前提条件是不行的——它仅是必要条件，只有Δx=0点的极限值也同时被排除(也是必要条件之一)，才能构成做除法消去分母的自变量Δx的充分条件，如此，我们还有可能通过消去分母的自变量Δx来求得有意义的极限2x吗？当然不行。因此，这就明白无误地证明了：公式2两边用中间的那个不等号分割完全是必要的、正确的——它们并不相等。也就是说，极限法第二代微积分求导对公式2从左至右的推导方向的前述充分必要条件并不能被满足。

三、在新诠释下给牛顿、莱布尼兹第一代微积分正名的现实意义及诸多优势

1．明确给出了牛顿、莱布尼兹之所以可以求出导数的确切原由，使其获得圆满解释，并给出与之协调的导数、瞬时速度、微分这些概念的全新定义及解释。导数就是比式(不必像极限法的“标准分析”那样明明都写出来了，即通常的分式dy/dx，还硬说不是比式)，微分就是增量(无论函数还是自变量的微分都一样)。而标准分析显然由于深层次的原因不得不假设或定义函数自变量的微分就是其增量，而函数的微分却只是其增量的一部分(所谓“线性主部”)，由此产生了一系列的问题。笔者坚信，任何有关理论最基础、最核心部分的新概念，只要正确反映了客观现实，就必然在后续研究中能够派上用场(与之对比，标准分析那套繁文缛节，之所以难以理解，现在是真相大白了：它根本就是错的)。现在，我们终于可以放心大胆地声明：牛顿、莱布尼兹微积分对且简，但需要新的解释；极限法微积分错而繁，问题已明确；

2．在理论上返璞归真，大大简化了微积分理论，使其易于理解。揭示并排除了其潜在的矛盾，使得今后的教学工作可以大为简化。整个与不可达极限有关的论述，几乎都可以省掉。只把牛顿、莱布尼兹(第一代)微积分彻底讲清(按笔者思路)就可以了。在真正意义上彻底实现了不用极限甚至无穷小概念的微积分(无穷小当然还可以有，但不是必须有)，彻底地填平了高等数学与初等数学间的鸿沟；

3．统一了微分与差分、微元法的区别，可以看出，微分本质上就是差分。不存在谁主谁次，哪个本质，哪个重要，哪个精确的问题了；可使得连续与离散间的理论鸿沟被抹平，过往连续概念必须借助于不可达极限概念才能建立，现在看来不是这么回事；点与长度、测度之间关系可以得到本质的理解，彻底解决了非线性函数以往在线性化过程中的精度、误差问题；

4．理论力学的静力学中有所谓虚位移、虚功概念。但明明是没有任何位移、没有做任何功，何来位移？哪怕是虚的？其“虚”在什么地方？显然，此概念无论用无穷小还是极限，都难以完满地、令人信服地予以解释：哪怕是无穷小的位移，也不是静止(0位移)；运动的极限，特别是不可达极限，也绝对不是静止(静止的当然可达)。实际上，用现有微积分的理论，怎么解释都十分牵强。但用笔者对导数的解释的思路，此问题迎刃而解：虚位移就是一个平衡的力系，假设一旦被打破不再平衡时的实际位移。相应地，虚功也一样。这与导数的新定义是吻合的；

5．欧拉、马克思甚至罗素都反对极限法求导理论。历史证明他们是对的：笔者指出了极限法求导无法自圆的逻辑矛盾，有力地证伪了极限法求导过程；

6．罗宾逊的非标准分析，等于又在暗中否定了标准分析(第二代微积分)的必要性。因为它由非极限的无穷小概念出发，也能得到相同的一切结论。它本质上是回到了第一代微积分的思路，用“取标准数”这个间接的概念过程达到牛顿等的舍弃无穷小的作用。它实质上是暗示，第二代的极限法微积分，并没有如其所宣示的那样否定的了牛顿、莱布尼兹的第一代微积分。因此本质上，极限法的标准分析(所谓第二代微积分)与无穷小的非标准分析不相容，是矛盾的。因为标准分析是以否定与非标准分析等价的第一代微积分为成立前提的。明确说，如果非标准分析成立，标准分析必不成立。理由是标准分析认为或承认第一代微积分不成立(否则还需要第二代微积分也就是标准分析吗)，而第一代微积分又与被认为是成立的非标准分析事实上等价。当然，非标准分析创建了整个无穷小理论，但在微积分求导过程中又与第一代微积分一样地舍弃了这个无穷小，而没有像笔者所做的那样给出任何令人信服的理由，这不能不是一种缺憾。在笔者前文的诠释下，此问题不复存在。因此，在新诠释下，无穷小仍可有一席之地，但不可达极限法求导，不应再出现于教科书中；

7．特别应该强调，笔者给出的微积分新诠释，实际只是对牛顿、莱布尼兹第一代微积分原本是正确的、但却被误解为错误的实际操作过程的理论解释。是对微积分诞生之初就早已践行的“老方法”的新诠释。并不应被误解成是笔者独出心裁地提出了一个新的求导方法。此外，在逻辑上它与所谓标准分析是互相独立的，即它与极限法的“标准分析”(第二代微积分)的对错无关。即：即使退一步说后者不错，也并不意味着笔者的理论解释错。而反之，后者如被证明有问题，在这种新诠释下的所谓第一代微积分就是唯一正确的。无论哪种情况，我们其实都可以郑重提示：教科书中的微积分理论，应该返璞归真，在简单明确的新诠释下，重新回到牛顿、莱布尼兹意义的第一代去，以求剔除矛盾、坚持本初、简化教材、有利教学。

以上论题受篇幅限制，未及详论。比如微分特别是自变量的微分合理性问题、积分问题、三角函数的求导问题、指数的求导问题、弧度的微分问题、力学中的虚位移问题、虚功问题等等，在新的导数诠释下的求出、解释，有兴趣的读者可以参考文末参考文献中列出的笔者论文及后续论文。