一道轻杆问题的正确解法与其引发的思考
2020-06-10王文娟
王文娟
(北京师范大学物理学系 北京 100875)
1 引言
物理学的研究,需要科学的方法作指导.学生在解决物理问题时,需要构建合理的物理模型,采用相关的物理方法,分析模型的物理运动过程.
轻杆模型是高中物理力学问题中的常见模型.现阶段的高中物理教学中,只讨论将物体简化成质点后的质点平动问题,暂不讨论转动问题.这使得高中阶段的绝大多数轻杆问题都对“轻杆”提出“忽略质量”的要求,使得杆的转动惯量恒为零,以期规避讨论杆的转动,便于高中学生求解[1].然而,多数教师、学生在求解轻杆问题时,由于习惯性地忽略轻杆的质量,忽视了轻杆可能存在的转动,甚至仅将这一模型视作质点平动问题进行求解,违背了这一模型的物理运动规律.
本文以2017年11月四川省绵阳市高三第一次诊断性考试(理科综合)第17题为例.通过与给出的标准答案对比,笔者认为该题选项C,D解析存在漏洞,不利于培养学生的物理思维.因此,本文将纠正其广为流传的错误解法,给出这一问题的正确解.
2 题目
【例题】如图1所示,光滑的小球A和B通过轻杆相连,靠在竖直墙和水平地面上,从图示位置由静止释放,则( )
A.轻杆对小球A始终不做功
B.轻杆对小球B做的总功为零
C.轻杆对小球A先做正功后做负功
D.轻杆对小球B先做正功后做负功
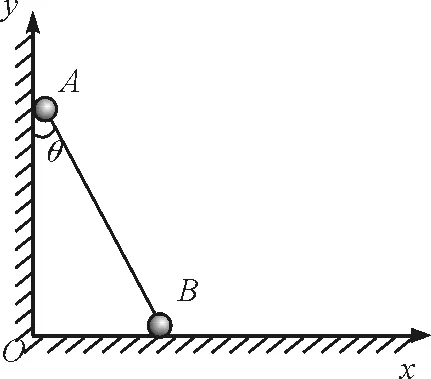
图1 例题题图
3 错解辨析
本题主要考察学生对受力分析、机械能守恒定律、运动学规律的应用能力.释放轻杆后,轻杆会顺势倒下.选项C,D的错解如下.
错解:当轻杆一直沿墙壁下滑时,A球速度沿y轴负向,B球速度沿x轴正向.将A,B两球速度分别分解为沿杆方向和垂直于杆方向,即
vA‖=vAcosθvA⊥=vAsinθ
vB‖=vBsinθvB⊥=vBcosθ
由于轻杆是刚性杆,不可伸缩,故沿杆方向两球共速,即vAcosθ=vBsinθ.则可知:当θ达到45°时,B的速度将减小,轻杆开始对其做负功;A的速度将增大,轻杆开始对其做正功.故C错误,D正确.
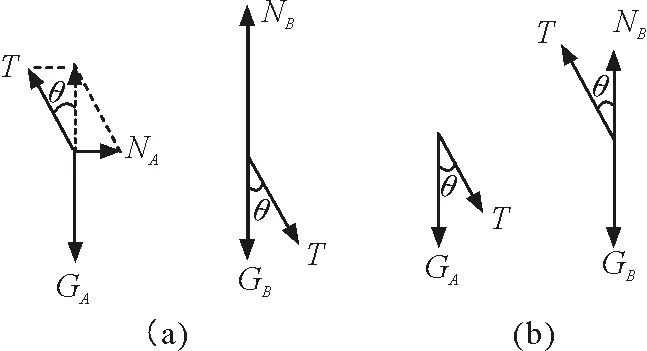
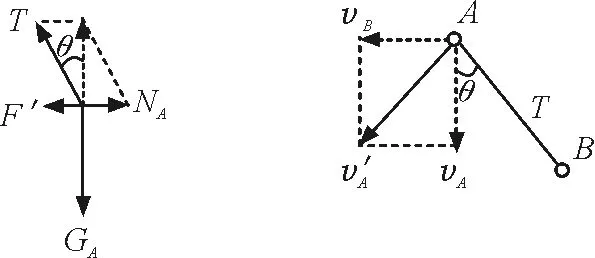
纵观错解,虽然巧妙运用了轻杆作为刚性物体的不可伸缩性,列出两球的速度关系式,看似严谨.但当θ达到45°时,只需保证vB 轻杆对物体做功的正负发生改变,也即轻杆对物体的作用力T的方向反向.那么,轻杆做功正负变化的临界角是否存在呢?如何对两球的物理运动过程进行精确的描述呢? 对两个小球进行受力分析,如图2(a)所示.GA,GB为两球重力,T为杆对球的弹力,NA为墙面对A球的支持力,NB为地面对B球的支持力.当轻杆开始下滑后,θ角增大,轻杆A端沿墙面滑下,B端沿地面滑动,A球所受合力FA沿y轴方向,B球所受合力FB沿x轴方向.弹力T对A球做负功,对B球做正功,使vB持续增大.由 vAcosθ=vBsinθ 可得 vA=vBtanθ 即随着θ的增大,vA也持续增大. 图2 两小球受力分析 大胆假设临界角θ0存在.θ=θ0后,弹力T反向,如图2(b)所示,轻杆做功的正负也发生改变,T对A球开始做正功,对B球开始做负功,即可证明选项D正确.同时,FA将会有x轴正向分量,使A球在x轴正向、y轴负向都拥有速度,轻杆A端不再单纯沿墙下滑,而是离开墙面,支持力NA消失;FB将会拥有x轴负向分量,使B球在x平面上出现减速运动. 那么,只要能够直接证明弹力T的方向在轻杆下滑过程中可反向,或证明使弹力T反向的临界角θ0存在,即可证得,在轻杆下滑直至落地前的全过程中,vA一直增大,vB先增大后减小,在临界角处取得最大值;即可得出轻杆对两球做功正负的变化情况,最终得出题目选项C错误、选项D正确的结论. 笔者将分别定性和定量分析. 图3 B球静止参考系中A球的合力与速度示意图 解法2(定量): 讨论简化情况.设A,B球质量为m,轻杆长l,初始时刻轻杆与墙壁夹角为α. 由机械能守恒定律,得 沿杆方向,杆长不伸缩 vAcosθ=vBsinθ O′系中:A球速度 向心加速度 临界状态θ=θ0时,T=0,A球合力F′A=GA,故有 a′‖=gcosθ0 可得临界角 解法3(定量): 讨论简化情况.设A,B球质量为m,轻杆长为l,初始时刻轻杆与墙壁夹角α. 由机械能守恒定律,得 沿杆方向,杆长不伸缩 vAcosθ=vBsinθ 联立上述两式得 有 本题选项A,B较易判断.在考场上,考生只需正确分析模型运动,便可以通过排除法排除,在选项C,D中得出答案,足以应付考场作答.但如果对本题仅仅只是应付了事,不仔细分析模型的运动规律,对于学生物理核心素养的培养将弊大于利;本题错误解答的广为流传,也暴露了当下物理教学的部分问题,以下问题值得引起物理教育工作者的重视. (1)“为解题而解题”,忽视核心素养的培养 物理核心素养,是学生在接受物理学习时,潜移默化形成的正确价值观念、必备品格和关键能力[2].以本题为例,错解虽然巧妙运用了轻杆的速度关系,但却忽视了运动状态发生改变的原因——力,忽视了物理学的这一支柱,完全没有对系统进行受力分析,进而导致错解的发生.在分析任何物体的运动状态前,我们都需要仔细分析物体的受力情况.在高中物理简化后的质点运动学问题中,我们只需要分析力的大小与方向,就能判断质点的平动是否发生变化;但在真实的物理场景中,受力分析变得更为重要:我们不仅需要判断物体是否会发生平动,还需要分析受力点的位置,判断物体是否受力矩影响,发生转动[1].受力分析在物理学中的地位可见一斑.作为教育工作者,我们有义务培养学生正确的物理观念,不能让错解带偏学生解决物理问题的思维方式. (2)局限于高中课本,较少主动探究模型背后的物理本质 新课标指出,通过高中物理课程的学习,学生应能运用科学思维与方法,建构合适的物理模型,从定性和定量两个方面对模型的物理问题进行推理,找到规律并得出结论[2].本题的轻杆下滑模型是一个非常贴近实际生活的模型.生活中与此最接近的模型,便是将一只笔用同样方式立在桌与墙之间,观察笔的自然下滑过程.分析时,可将笔视作一个质量均匀分布的长条刚体,进而可以研究笔的平动与转动.这是一个带领学生主动跳出高中物理课本范畴、了解刚体转动问题的好机会,但碍于高中教学环境所限,绝大多数教师并未将此纳入教学环节,错过了增长学生见识的时机.教师有义务在完成规定的教学任务的同时,带领学生进行科学探究活动,拓宽学生的知识面,让学生的物理素养得到进一步的提升.4 模型运动分析
5 正确解答

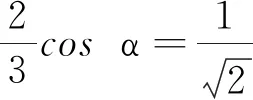
6 总结与展望
