基于Origin的夫琅禾费圆孔衍射仿真实验及在教学中的应用
2020-06-10刘慧丰
刘慧丰
(中北大学信息商务学院 山西 晋中 030600)
从波动光学角度出发,由于衍射现象的存在,一个点光源过圆孔后在光屏上形成的像是一个有一定大小的艾里亮斑,而光学仪器中所用的光阑、透镜,包括眼睛,都可以等效为一个透光的圆孔,因此光学仪器成像时的清晰程度最终要受到圆孔衍射所限制,其分辨本领与圆孔衍射问题息息相关.光学系统成像时大部分是平行光或者近似的平行光入射,所以研究夫琅禾费圆孔衍射对于光学成像和光学仪器设计至关重要.为了将圆孔衍射中现象和成像规律形象直观地展示给学生,加强学生对知识的理解,从而提高学生的学习兴趣和探索知识的积极性,在教育手段和网络技术不断普及的现代,仿真技术也逐渐应用到了教学中.人们通常将物理仿真实验与传统教学手段相结合,利用Matlab,Maple,Mathematica等软件模拟仿真[1~3],但是这些软件对使用者的要求较高,需要一定的编程基础进行大量的编程,对于低年级学生来说有点困难.Origin软件是国际科技出版界公认的标准作图软件,功能强大但操作简单快捷,具有可重复性强、参数易调节、观察性更强、省时省钱且简单易操作的优点,深受用户欢迎.
本文基于夫琅禾费圆孔衍射光强分布的理论公式,通过Origin软件中的多工作表矩阵(Matrix)窗口对衍射图样进行仿真,对图样中光强分布图结果进行数值计算,且验证了艾里斑的半角公式,加强了学生们对夫琅禾费圆孔衍射的理解.
1 基本原理
在图1(a)中,一束波长为λ的平行光垂直入射到半径为R的圆孔上,通过圆孔后被透镜L汇聚,在其焦平面上可得到圆孔衍射图样,图样是一组同心的明暗相间的圆环,以第一暗环为范围的光强占入射光光强的绝大部分,称之为艾里斑,如图1(b)所示.
根据惠更斯—菲涅尔原理可知圆孔衍射在光屏上任一点P的光强为[4]
(1)
式中
将上式用一阶贝塞尔函数符号表示,则得
(2)
式中
其中r为P到坐标原点O的距离.
(3)
在讲授这部分内容时,因为教材对这部分知识点描述时理论推导过于繁琐且涉及到了很多高数中的知识,学生学习起来感到枯燥乏味且非常吃力.为了在转变单一的物理教学方式的同时使学生更好地掌握这部分知识,可以在课堂上实时演示,但是实践起来费钱费时,因此推广起来不易.为此,利用计算机软件进行仿真实验势在必行.
2 衍射图样仿真及分析
2.1 实验仿真
基于圆孔衍射的光强分布公式,本文采用的模拟方法是Origin9.0软件对衍射图样进行仿真,具体步骤如下:启动Origin9.0软件后,首先,点击菜单栏中的File/New/Matrix,建立一个矩阵,设置矩阵维数为(501,501),坐标x,y的范围均设定为(-0.2,0.2);然后,左击Matrix,选择Set Values,依据光屏上点P对应的光强分布公式(3)将矩阵元的值设定为4*I0*(J1((2*pi*R*sqrt(x^2+y^2))/(λ*f)))^2/((2*pi*R*sqrt(x^2+y^2))/
(λ*f))^2,左击OK确定生成表征干涉光强的数据矩阵;最后,点击Plot 菜单下的Image /Image Profiles,即可获得仿真衍射图像[5,6].分别改变光强公式(3)中R,λ参数,分析衍射图样随圆孔半径和入射光波长的变化情况.
2.2 影响艾里斑大小的因素
设入射光的光强I0=1,透镜L的焦距f=1 m,分别定义参数R,λ不同数值,得到衍射图样的一系列仿真图如图2所示,其上方和右方的分别是y=0处光强随横坐标x和x=0处光强随纵坐标y的变化函数图.分析比较不同的R,λ对衍射图像的影响.
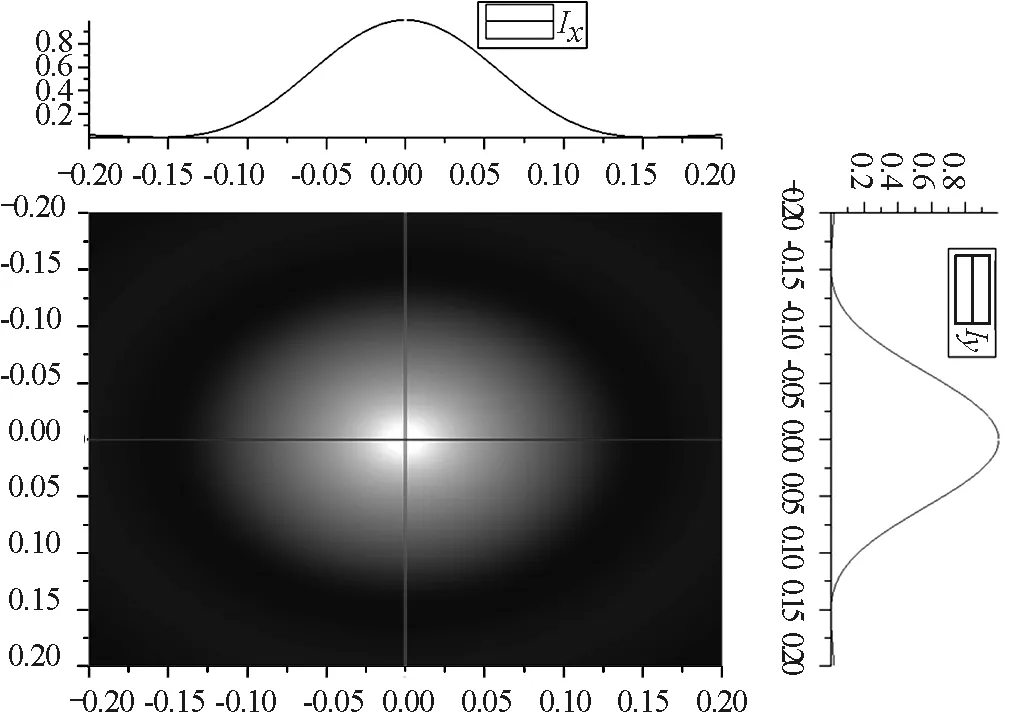
(a)R=0.003 mm,λ=760 nm
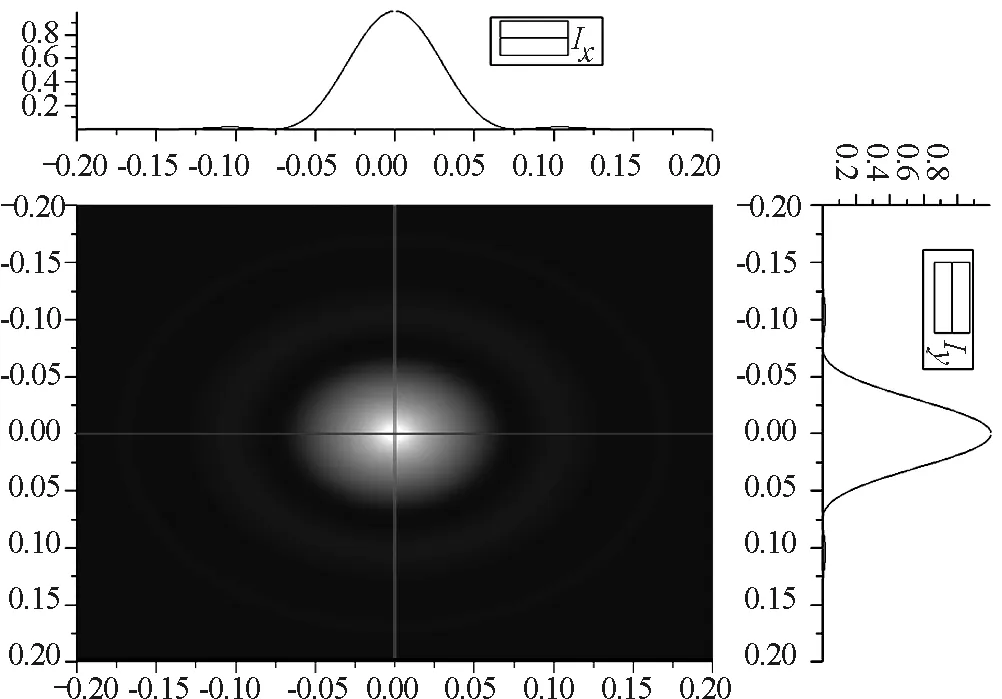
(b)R=0.006 mm,λ=760 nm

(c)R=0.003 mm,λ=400 nm
由图2可见,圆孔衍射图样是明暗相间的同心圆环,中央的亮斑光强极大,占据衍射能量的绝大部分,周围亮环的强度随着离中心距离的增大急剧减小,第二级明纹的光强已很小,在衍射图样中几乎看不到.改变圆孔半径和入射光波长,艾里斑的大小也随之改变.通过比较图2(a)和(b)可得,当波长相同时,艾里斑的尺寸随圆孔半径的增大而减小;通过比较图2(a)和(c)可得,当圆孔半径相同时,艾里斑的尺寸随波长的增大而增大.
利用Origin模拟仿真可将衍射图样实时地展示在课堂上,使学生们对艾里斑有了形象生动直观的认识.同时,学生们可以自己尝试输入不同的圆孔半径和入射光波长,观察这些参数如何影响衍射图样,激发学生们探索知识的兴趣.
2.3 极值位置 光强分布及艾里斑公式
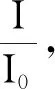
col(A))/(4e-7*1))^2,选定数据后在菜单栏里点击Plot里的Spline Connected,得到夫琅禾费圆孔衍射的光强分布如图3(a)所示.由于光强比值随半径的增大而快速下降,为了更加清楚地观察其他衍射亮环光强的分布特征,将图3(a)中纵轴的取值范围缩小为[0,0.020],如图3(b)所示.
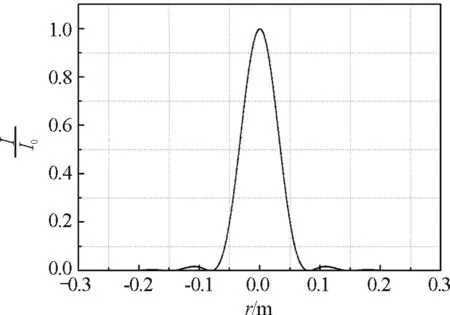
(a)
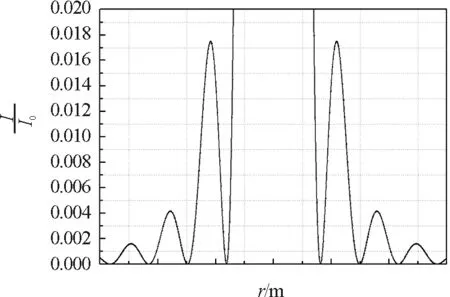
(b)
利用界面里面的“Data Reader” 在图3(b)中读取前6个极值对应的坐标和相对应的光强比值.透镜L的焦平面上明纹和暗纹位置以及强度分布情况如表1所示,与教材中给出的结果一致[4].

表1 前6个极值的位置及相对光强度
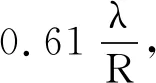
利用Origin描绘夫琅禾费圆孔衍射的光强分布曲线,得到的实验结果与教材中的结果一致,将仿真实验和理论教学相互补充、支撑,学生们能够更加充分理解和巩固所学知识,从而提高教师教学的效率与质量.
3 结束语
本文基于惠更斯—菲涅尔原理,得到了夫琅禾费圆孔衍射光强分布的理论公式,接着使用Origin软件中的多工作表矩阵(Matrix)窗口对衍射图样进行仿真,定性分析了艾里斑的大小与入射光波长和圆孔孔径的关系,然后使用“Data Reader”读取了光强分布图样中明纹和暗纹位置以及强度分布,且验证了艾里斑的半角公式.将仿真实验软件与大学物理课堂教学相结合,可以将教材上的结论直观地展示在课堂上,激发学生的学习兴趣, 加深了学生对夫琅禾费圆孔衍射现象和规律的理解.
