精心设计演示实验 促进科学思维发展——以“单摆”教学设计为例

谭国锋

(杭州第二中学 浙江 杭州 315009)

梁旭

(浙江省教研室 浙江 杭州 310012)

物理学科核心素养是学生在接受物理教育过程中逐步形成的适应个人终身发展和社会发展需要的正确价值观念、必备品格和关键能力，是学生通过物理学习内化的带有物理学科特性的品质，是学生科学素养的关键成分，物理学科核心素养主要由“物理观念”“科学思维”“科学探究”“科学态度与责任”这4个方面的要素构成[1].

“科学思维”是从物理学视角对客观事物的本质属性、内在规律及相互关系的认识方式，是基于经验事实构建物理模型的抽象概括过程，是基于事实证据和科学推理对不同观点和结论提出质疑、批判、检验和修正，进而提出创造性见解的能力与品质.“科学思维”主要包括模型建构、科学推理、科学论证、质疑创新等要素[2].教师如何在核心素养的指导下进行课堂教学设计，如何创设问题情境和进行问题引导，促进学生科学思维的发展，笔者以“单摆”教学设计为案例谈谈自己的认识和实践.

1 教学分析

1.1 教材分析

单摆是简谐运动的应用实例，既是对本章所学知识和方法的综合应用，又是对简谐运动具体模型的拓展.

1.2 学情分析

学生已经知道简谐运动的特点及从运动角度和受力角度证明简谐运动的两种方法，这为“单摆”的学习打下了扎实的理论和实验的基础；通过简谐运动的学习，学生知道了简谐运动的等时性，为确定单摆做何种运动提供了一定的支撑；之前学习的控制变量、转化等物理思想和方法，为本节课的实验探究提供了方法的支撑.本节课也存在学生困惑的地方：单摆为什么在小角度的时候可看作简谐运动？回复力的方向如何确定？

2 教学目标

2.1 知识目标

摆长、摆角、周期、振幅等概念，周期公式规律，单摆模型.

2.2 科学思维

能根据大量生活中的摆动原形，通过与弹簧振子做类比，构建“单摆”这个理想化模型(模型建构).

能从单摆周期与不同角度的关系，分析得出单摆小角度时摆动具有等时性的规律(科学推理).

能从单摆等时性的结论，分析出单摆可能做简谐振动(科学推理).

能从回复力角度推导出单摆小角度摆动时做简谐振动(科学推理).

会利用实验中获得的x-t图像，通过正弦曲线拟合证明其是正弦函数(科学论证).

尝试分析周期与摆长关系的图像并不过原点的原因(科学论证).

能对蛇摆的工作原理提出自己的设想，并进行论证(科学论证).

2.3 科学探究

能观察现象，提出可探究的问题，作出有依据的假设，用控制变量的方法设计探究周期与质量、摆长关系的方案(科学探究).

能对观察到的摆角与周期数据进行分析，形成周期与摆角关系的结论(科学探究).

设计思路：以核心素养的教学目标为指导，基于学生想探究的问题，从学生的视角设计思维上的冲突：如为什么会有这样的现象？现象背后隐藏着怎样的规律？如何去探究这些规律？让学生充分地参与到探究和学习活动中，使核心素养落实到每一个教学环节.

3 教学过程

3.1 模型构建

情景(图片或视频)：(1)单杠上运动员摆动;(2)吊灯摆动;(3)海盗船;(4)荡秋千;(5)摆钟.

师：物理学的研究总是从简单到复杂，今天我们先来研究最简单的摆动.

问题1：前面各种摆动中哪个最简单？这个摆动是否还可以简化？如何简化？

学生：吊灯和摆钟比较简单，可简化为“绳+球”模型.

逐个展示如图1所示的多种“绳+球”组合摆动，观察并思考哪种情况的运动最简单，是否还能更加简单？

图1 多种“绳+球”组合

学生甲：“细绳+乒乓球”，乒乓球摆动时空气阻力影响很明显，很快就停下来，所以小球的密度要大，如用铁球.

学生乙：“铁球+橡皮筋”，铁球在运动时既有摆动，又有沿橡皮筋方向的伸缩，所以绳子不能有弹性.

学生丙：“铁球+粗绳”，绳子的质量比较明显，运动时各部分速度大小不同，动能很难计算，所以最好能够用质量可忽略的绳子，如细绳.

学生丁：“铁球+短线”，球在运动时既有摆动，也有相对绳子下端(与球连接处)的转动，因为与绳子相比，小球已经不“小”.

师：前面我们用理想化的方法得到了弹簧振子模型，我们把理想化的最简单的摆称为单摆，它的条件是什么？

学生：1)忽略空气阻力的影响；2)不计绳子的质量；3)小球可看成质点；4)绳子无弹性.

师：实际中是否存在单摆？怎样的装置可近似看成单摆？

3.2 单摆周期与振幅关系的探究

师：如图1中最右边的摆可近似看作单摆，当把小球拉开小角度后释放，运动有何特点？想到了用什么物理量来描述？

学生：往复运动；周期.

师：如果要让这个摆的周期变小点，可以怎么操做？

学生：减小摆角.

演示实验：周期用光电计时器测量，如图2所示，数据如表1所示.

图2 光电计时器测量单摆周期

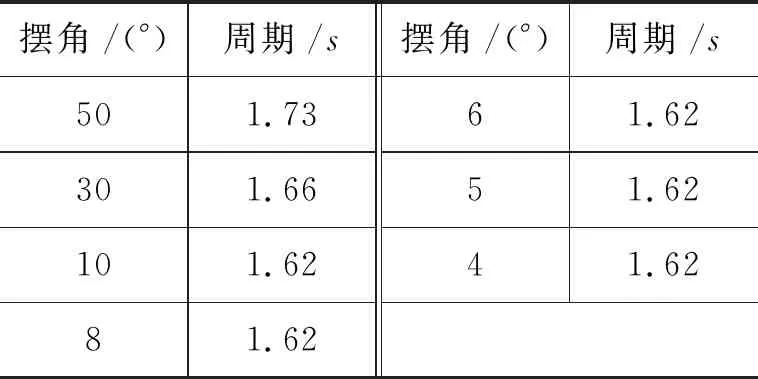
表1 单摆周期测量实验数据

演示：50°,30°,10°时的周期测量.

师：周期与摆角有关系吗？

学生：摆角越小，周期越小.

师：通过3组数据得出结论在科学研究中并不严谨，我们需要更多的数据来支撑我们的结论.

演示：8°和6°时的周期测量.

师：有没有新的想法？

学生：随摆角变小周期可能趋于一个定值不变，但是两组数据还不够，我们需要更多证据.

演示：5°和4°时的周期测量.

师：实验数据证明大家的猜想是正确的，小于10°的时候，仪器的读数已经不随摆角改变，具有等时性.最早发现这个规律的是意大利物理学家伽利略，他通过观察教堂吊灯的摆动发现了摆的等时性，奠定了制造摆钟的坚实基础，为人类更加精确地计时开辟了道路.

3.3 单摆做简谐运动的证明

师：小角度摆动时周期不随角度变化，这让你有怎样的猜想？

学生：因简谐运动的周期与振幅无关，小角度摆动时的单摆具有等时性，所以很可能是简谐运动.

师：物体做简谐振动，我们可以用什么方法来证明？

学生：从运动的角度，须证明x-t图像是正(余)弦；从受力的角度，须证明回复力满足

F=-kx

3.3.1 简谐振动的实验证明(运动的角度)

演示实验:如图3所示,紫外线发射器的小角度摆动可看成单摆.

图3 简谐振动实验

紫外线照射到显影布上可以显示点迹；电动机拉动显影布，得到图4所示点迹.

图4 实验得到的轨迹

师：如果将打出的点迹连成x-t图像，像正(余)弦函数吗？用什么方法能够更加严格地证明？

学生：与标准正(余)弦函数图像进行比对.

教师把图像拍照后放到PPT上，与用几何画板作出的标准正弦曲线去比对，如图5所示.

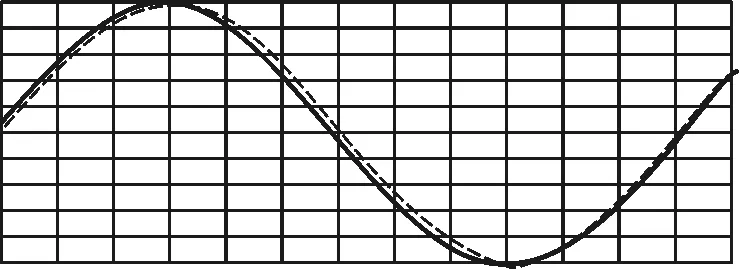
图5 实验结果与标准正弦曲线比对

3.3.2 简谐振动的理论证明(受力的角度)

师：单摆摆动时，平衡位置在哪里？受到的合力是否为零？

学生回答后教师总结：平衡位置在最低点，合力不为零.

师：单摆在某一位置的时候，回复力由谁来提供？

学生：重力分力提供，大小为mgsinθ

师：sinθ与θ之间有怎么样的联系？

展示不同角度的sinθ与θ值，如表2所示(10°以内，相对误差小于0.5%，sinθ≈θ).

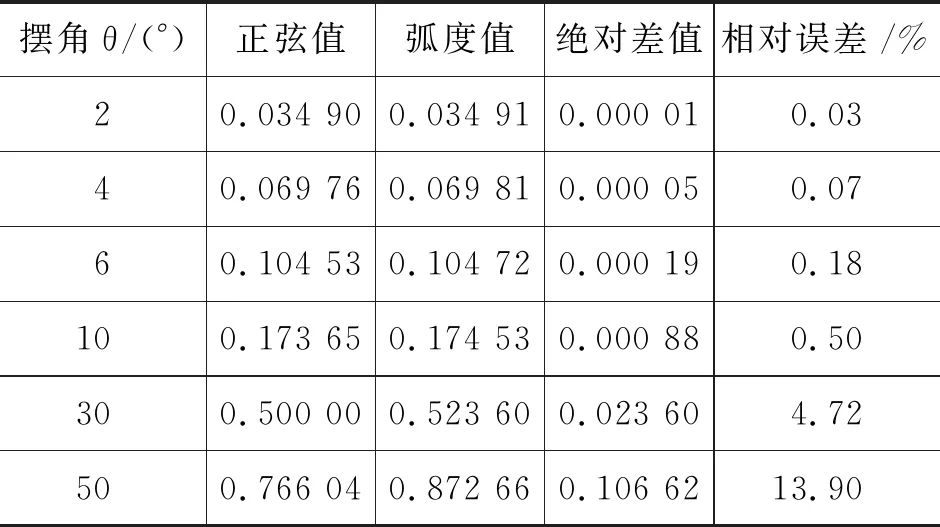
表2 不同角度的sin θ与θ值

师： sinθ与x之间有怎么样的联系？

用几何画板动画展示不同角度时的弦长和弧长关系,如图6所示.

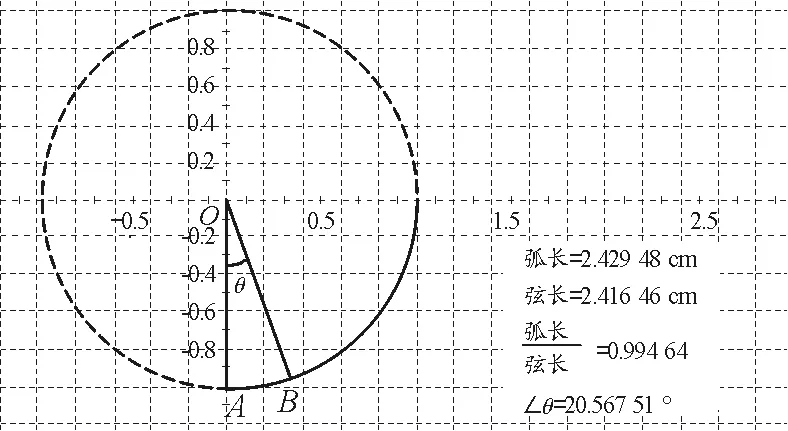
图6 不同角度时的弦长和弧长关系

当角度很小时

x≈l=Lθ

师生共同总结小量近似的科学思想，学生小组讨论，完成理论证明

F回=-mgsinθ

(1)

(2)

由式(1)、(2)联立得

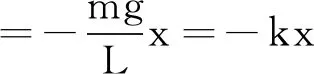
3.4 探究影响周期的因素

师：单摆小角度摆动时，周期可能与哪些因素有关？

学生猜想：与质量、摆长、重力加速度有关.

师：请设计实验方案.

学生总结：用控制变量法，控制其他物理量一定，研究周期与其中一个因素的关系.

3.4.1 探究周期与质量关系

师：请介绍你们的实验方案.

学生：测两个摆长相同，质量不同的小球的周期(如图7所示)， 实验结果周期近似相等.

图7 周期与质量关系实验

3.4.2 探究周期与摆长关系

师：请介绍你们的实验方案.

学生：装置如图8所示，改变摆长，测量周期，数据如表3所示.

图8 周期与摆长关系实验

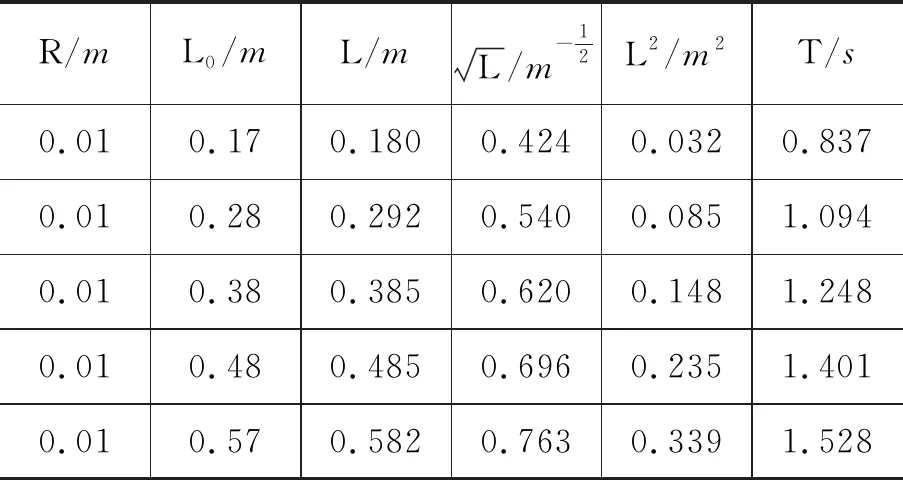
表3 周期与摆长关系实验数据

师：根据数据在T-L图像上描点，如图9所示，根据点迹，分析T与L有何关系？

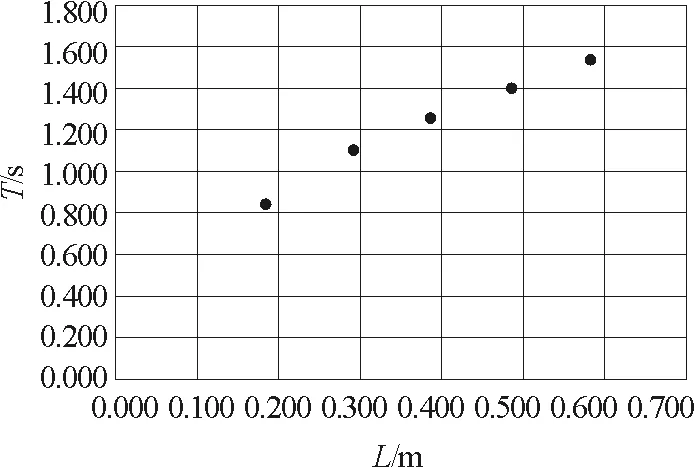
图9 T与L关系图像

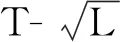
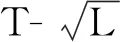
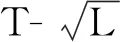
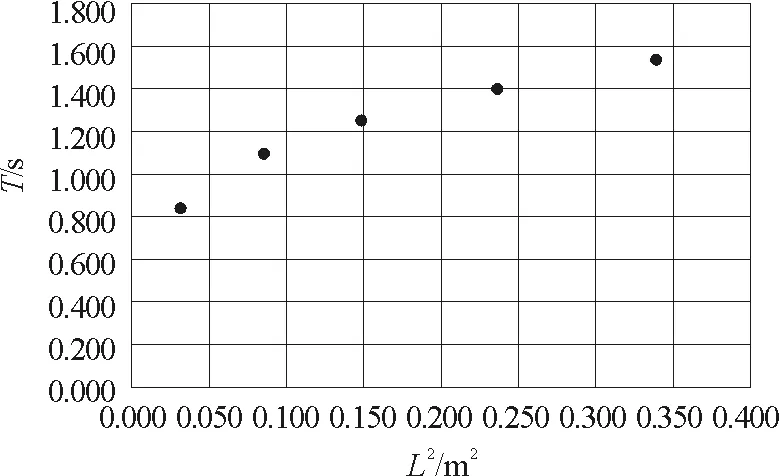
图10 T与L2关系图像

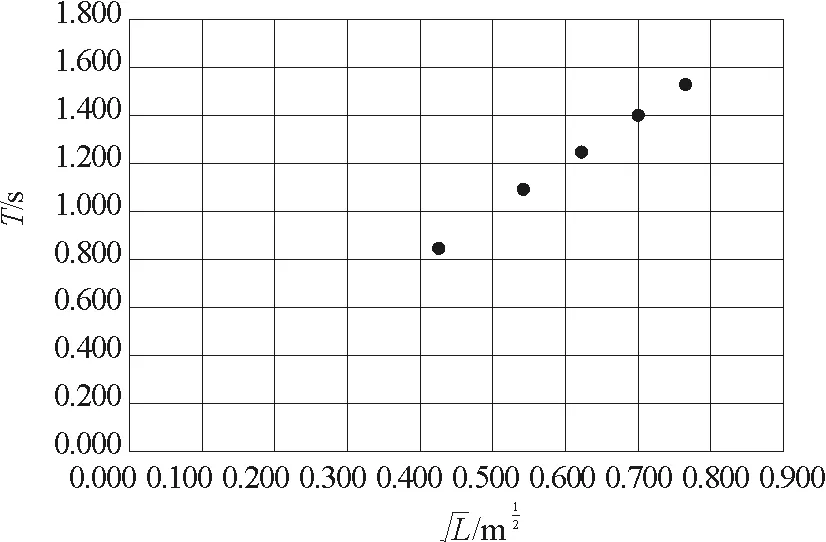
图11 T与关系图像

直线拟合，得出直线的函数方程，如图12所示.

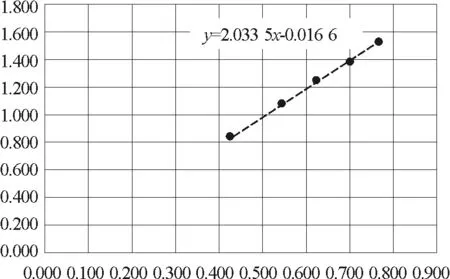
图12 直线的函数方程

师生共同总结：

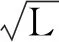
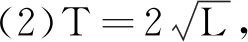
3.5 探究成果的应用

演示：群摆，如图13所示，这群小球好像有个约定，按一定的规则进行这场舞台秀，连续不断呈现不同图案.每个小球都可以看成单摆，在做简谐振动.其设计的技巧在于每个球做简谐振动的时间差为0.1 s.请你结合本节课所学知识，思考制作时，各个摆的摆长应该如何选取，填入表4.小组合作，课后设计、制作简易群摆.

图13 群摆

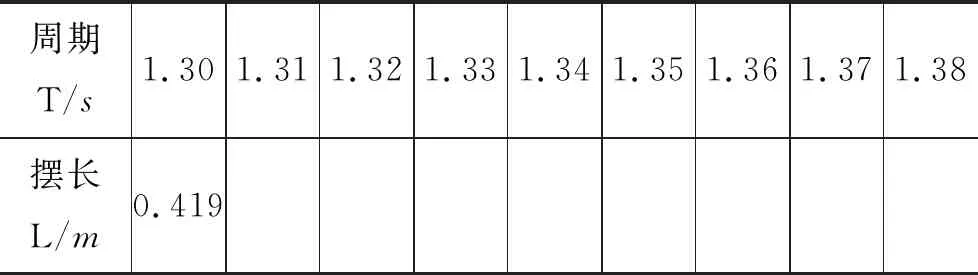
表4 群摆实验数据

学生讨论后形成的设计方案：

方案一：用一个球测出重力加速度，然后根据不同的周期，可以算出周期对应的摆长.

方案二：不测重力加速度，用摆长与周期的比值是定值，通过计算得出不同周期对应的摆长.