初中数学面积问题蕴含的数学思想方法及教学分析

汪强

【摘要】虽然经历多年的学习，但还是有相当一部分学生对于面积问题掌握得不太理想，究其原因，学生对于面积问题中蕴含的数学思想方法挖掘不深，导致做一题会一题，学习效率较为低下。本文旨在通过对北师大版《数学》课本中面积问题的呈现方式和蕴含的数学思想方法进行分析，使教师在教学中引导学生关注背后的数学思想方法这条暗线，使得面积问题的学习有的放矢、事半功倍。

【关键词】面积;数学思想方法;转换与化归

一、问题提出

面积问题是初中数学教学的重点内容，在一系列知识的发生、发展过程中起到相当重要的作用，同时也是各年级期末考试和中考的考察热点和考察难点。另一方面，虽然已有7年的学习经验，面积问题对于大部分学生仍然是难点。为什么会造成这种现象？教师对数学知识、数学问题的认识站位太低，只关注具体的知识、具体的题目，未能洞察其中所蕴含的数学思想和数学方法，似乎给了我们一条解决问题的钥匙：找到这些数学思想方法，并让它们指导理解知识、指导解题。那么在初中数学面积问题有哪几种类型的呈现？其中又蕴含了哪些重要的数学思想和方法？本文尝试回答上述问题。

二、初中数学面积问题呈现方式及蕴含数学思想方法

以北师大版《数学》为例，问题是数学的心脏，学习数学的主要目的在于问题解决。好的数学问题应当具有较强的探索性，具有现实意义或与学生的实际生活有着直接的联系，具有趣味性和知识性。面积问题是数学知识的结构中的重要“连结点”，常结合整式、方程、函数、三角形全等和相似、四边形、圆等初中数学的核心内容展开学习与考察。

1.直接求某个图形面积以使新知识可视化

由于小学阶段学生已经学习了矩形、正方形、平行四边形、三角形、圆的面积公式，并对转化、等积变换、割补等方法有了一定的了解，初中阶段为了使得一些抽象的知识可视化，在整式的相关原理、方程与函数等概念的引入时大量采取了面积问题，通过考察三角形、矩形、梯形、圆或以上图形的组合图形的面积，探索新的概念、原理，也通过面积问题进一步巩固新知。

例1：图中长方形由两个小长方形组成，求这个长方形的面积。

教学分析：本例是北师大版《数学》七年级上册P90《3.4整式的加减》的引例，旨在引发学生思考图形面积的不同表示方式，从而通过概念同化得出合并同类项法则，这里充分体现了可视化的教学原则，将“合并同类项”这个抽象的代数原理通过矩形的面积呈现，接下来的几节课也很好地体现了这些思想方法。

解决这个问题本身不是难点，关键是认识到此类问题的意义，并在教学中通过问题串引导学生发现：

（1）这个图形面积有哪两种不同的表示方式？你能得到怎样的等式？

（2）你能从中总结出合并同类项法则吗？

（3）你能通过图形来解释合并同类项法则吗？

其中体现的是数学模型思想方法、类比思想方法、特殊与一般思想方法，这对于学生后续学习整式乘除、方程、函数等概念、原理颇有裨益。

2.借助图形面积不变性揭示数学原理

通过图形进行公式验证一直以来是数学中的令人着迷的篇章。它以其直观、洞察的魅力让众多数学家趋之若鹜，如勾股定理的证明方法就有500多种，是数学中证明方法最多的定理之一，而初中阶段课本中也充分展现了前人对于这一问题的研究成果，并试图利用它进一步锻炼学生的思维品质、增强学生的数学素养。

例2：你能用右图解释公式（a+b）2=

a2+2ab+b2吗？

教学分析：本例是北师大版《数学》七年级下册P23《1.6完全平方公式》的“想一想”，是在学生已经通过代数方式得到完全平方公式的一个有效补充，其中充分体现了数形结合数学思想方法中“以形助数”的直观性，通过图形学生得出第一个直观印象：（a+b）2≠a2+b2，通过面积不变性不难读出公式（a+b）2=a2+2ab+b2。

2.3 以面积为载体考察综合运用知识能力

作为初中阶段数学知识的“万金油”，面积问题几乎出现在初中阶段所有章节，如以面积为背景的方程、函数问题，又如，为了求面积必须求高或底的几何综合题。

例3：如圖，在一块长35米，宽26米的地面上，修建同样宽的两条垂直的路，剩余部分种花，要使剩余面积为850立方米，道路的宽应为多少？

教学分析：本例是北师大版《数学》九年级上册P38 “问题解决”第2题，在此之前学过空白部分的十字图形面积求法，也学习过图形的平移，因此本题的关键在于将求四块图形面积和转化为求空白面积或转化为求四块拼成的一个大长方形的面积，因此，这里的关键就是转换与化归思想方法的落实。

例4：如图，阴影长方形的面积是多少？

教学分析：本例是北师大版《数学》八年级上册

P14 “知识技能”第1题，在此之前学过矩形的面积，

因此本题的关键在于将求矩形面积转化为求矩形的长，

即用勾股定理求解直角三角形斜边长，因此，这里的关键也是转换与化归思想方法的落实。

通过以上两个例子不难看出以面积为载体考察综合运用知识能力重点考查了学生的转换与化归能力，只要能把面积问题转化为已解决数学模型或已学习数学知识，一切皆可迎刃而解。

通过对教材中呈现的面积问题的分析，不难发现，其中将知识点串成“项链”的线就是数学思想方法，学生在学习过程中感觉面积问题的困难或多或少与数学思想方法这根暗线难以把握准确有一定关系，正如“山重水复疑无路，柳暗花明又一村”，当解题时数学思想方法这根暗线浮现，解题就变得得心应手。

三、初中数学面积问题数学思想方法教学分析

数学思想方法包括全域性数学思想、局域性数学思想、一般性数学方法、特殊性数学方法。面积问题为学生提供了一个观察、分析、猜想并进行说理验证的探究模型，以图形的运动变化为策略，让学生能在一个动态的数学情景中感悟知识的发生、发展过程，探索问题的结论和规律的变与不变，真正理解图形的性质。与此同时发展学生的空间观念，培养学生探索、猜想能力和创新思维能力。以下从初中阶段考察较多的三种数学思想方法开展分析。

1.数形结合思想方法

数形结合思想方法分为三种类型：以形助数，以数解形，数形互助。[1]在初中面积问题中，以“以数解形”呈现方式为主，对于学生来讲也较为容易接受，而“以形助数”显然需要具备更高的数学洞察力和更强的直觉思维。

例6：计算12+12+22+32+52+82+132+212+342+552

教学分析：从式子上来看这是一个斐波那契数列的平方求和问题，如果单纯从式子上考虑，会想到从特殊到一般的数学思想方法进行研究：先计算12+12=2=1×2，12+12+22=6=2×3，12+12+22+32=15=3×5……

从而观察出这个数列求和的规律（由于斐波那契数列的通项是难点，故不考虑从一般到特殊的方法）。

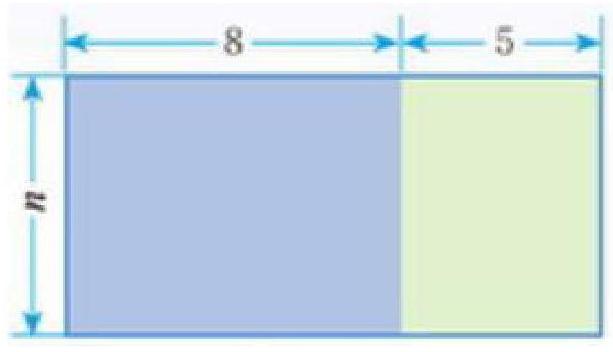
在教学中，能够观察出式子右边特点的个案并不多。如果采用数形结合的思想方法，理解起来就容易的多，通过画图不难发现，每个平方式对应一个正方形的面积，将前5个正方形拼在一起就得到如图所示的长方形。通过观察发现它的长为8（第6个斐波那契数），宽为5（第5个斐波那契数），因此，可以猜测上式也可以表示一个长方形的面积，它的宽为55，长为55+34=89。

解：如图，可知12+12+22+32+52+82+132+212+342+552表示宽为55，长为89的长方形面积，因此：12+12+22+32+52+82+132+212+342+552=55×89=4895

2.转换与化归思想方法

初中阶段面积问题延续小学阶段的多彩斑斓，在转换与化归的思想方法上呈现出多种姿态：不规则多个规则（或易求），不规则规则，不规则规则，线段比面积比。

例7：如图，△ABC中，点E、P在边AB上，且AE=BP，过点E、P作BC的平行线，分别交AC于点F、Q，记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3。

（1）求证：EF+PQ=BC;

（2）若S1+S3=S2，求的值;

（3）若S3-S1=S2，直接写出的值

教学分析：通过审题不难发现第一问关键在将等式转化为证明=1，进一步转化为证明=1，由于AE+AP=BP+AP=AB，因而得证。此题的难点在于第2问及第3问，通过分析发现可类比第1问将等式变形并转化面积比为线段比从而得以解决。

解：（2）∵S1+S3=S2

问题（3）解答与问题（2）类似，在此不再贅述。

3.3 分类讨论思想方法

例8  如图，由点P（14，1），A（a，0），B（0， a ）（a >0）确定的△PAB的面积为18，求a的值

分析：本题的关键在于给出的图形是示意图，线段AB与点P的位置关系是否如图所示为未可知，因此需要就点P与线段AB的位置进行讨论。

列方程得，解得a3，a4

综上可知a的值为3或12或

四、结语

“能使学生获得受用终生的东西的那种教育，才是最高尚最好的教育”。而面积问题正是数学思想方法极佳的载体，通过面积问题教学这样一件富有意义的工作，为人师者可以帮助学生巩固四基，启迪他们的思维。将来不管学生从事什么工作，唯有深深地铭刻于头脑中的数学精神、数学的思维方法、研究方法，能随时随地会发生作用，受益终生。

参考文献：

[1]董磊.初中数学主要思想方法的内涵及其层次结构[J].中学数学教学参考（中旬），2018（9）：67—70.

[2]顾泠沅，邵光华.作为教育任务的数学思想与方法[M].上海：上海教育出版社，2016.