考虑堆场缓冲区容量的ASC与AGV集成调度

文家献，魏 晨，尹宇起，胡志华

上海海事大学 物流科学与工程研究院，上海201306

1 引言

自动化集装箱码头中，堆场由多个箱区组成，每个箱区海侧端配备一台自动化堆垛起重机（Automated Stacking Crane，ASC），用于搬运集装箱；每个箱区海侧端设有自动化导引小车（Automated Guided Vehicle，AGV）缓冲区，用于AGV与ASC交接集装箱，缓冲区与岸边之间的区域为AGV 行驶区。卸船过程中，当缓冲区中集装箱数量等于缓冲区容量时，AGV 无法进入缓冲区作业，在缓冲区外等待。因此，考虑缓冲区容量约束的AGV 调度是自动化集装箱中的现实问题，合理安排ASC与AGV的协同调度对提高AGV利用率、实现自动化集装箱码头整体效益最优具有重要的指导意义。

2 研究现状

关于自动化码头ASC 的调度，现有文献主要考虑双ASC协同作业。胡志华等考虑任务之间的最小时间间隔，以最小化ASC 完成时间为目标尽力混合整数规划模型，设计启发式算法和遗传算法进行求解[1]。魏晨等考虑双起重机时空同步约束条件，以最小化作业总完成时间为目标，建立双起重机调度混合整数规划模型，确定起重机在每个时间点上所处贝位及其作业状[2]。Gharehgozli等以最小化总任务时间和ASC等待时间为目标，建立混合整数规划模型，并通过实验验证不设置交接区比设置交接区得到更好的结果[3]。

关于自动化码头AGV 调度，现有文献的研究方式多为建立混合整数规划模型、设计启发式算法或遗传算法进行求解，以优化AGV 作业序列。Zaghdoud 等提出迪杰斯特拉算法、遗传算法和启发式算法求解自动化集装箱码头AGV 的调度问题[4]。Roy 等考虑同时装卸过程中的动态调度，建立混合整数规划模型，优化任务分配[5]。Rashidi等建立最小成本流模型，设计基于标准网络单纯形法的启发式算法求解自动化集装箱码头中AGV 的调度问题[6]。Choe 等考虑自动化集装箱码头的不确定性环境，设计基于在线偏好学习的启发式算法求解AGV作业序列[7]。包晓琼等考虑集装箱的不同尺寸，以最小化整体作业完成时间、空载时间和最大化闲置时间为目标，建立多目标混合整数规划模型，优化车辆配对调度方案[8]。

缓冲区容量约束在流水车间中有广泛的应用研究。Engin 等考虑缓冲区容量，以最小化最大完成时间为目标，设计蚁群算法研究流水车间的调度问题[9]。郑永前等考虑到缓冲区、机器可用性约束和序列相关换模时间，以最小化最大完工时间为目标建立混合整数规划模型，设计启发式算法研究流水车间调度问题，并通过实验验证算法的有效性和鲁棒性[10]。谢展鹏等针对有限缓冲区流水线调度问题，设计基于变邻域搜索策略的启发式算法进行研究[11]。曾程宽等提出基于邻域搜索的两阶段算法对车间调度问题进行求解，算例分析表明，当缓冲区间容量与工件数量的比例达到20%，缓冲区间大小对调度结果的影响将会迅速变小[12]。

本文考虑时间窗和缓冲区容量约束，研究ASC 与AGV 的协同作业，以最小化总任务完成时间和最小化总任务延迟时间为目标建立混合整数规划模型，确定缓冲位的分配，优化ASC的作业顺序，提高码头作业效率。

3 问题描述

卸船作业中，进口集装箱由岸桥从船舶卸载至AGV上，然后，由AGV沿车道运输至缓冲区，卸载至指定缓冲位；场桥从箱区移动至缓冲区，提取集装箱，将集装箱搬运至指定位置（如图1）。在调度过程中，考虑AGV 匀速行驶且数量充足，AGV 预先在岸边等待，因此，岸桥可连续作业。由于缓冲区容量有限，AGV到达缓冲区后，若无空闲缓冲位，则AGV等待。但每个任务要尽可能在给定的时间窗内完成，AGV 的等待将影响任务的完成时间，因此，如何安排缓冲位与AGV的分配关系以及ASC 的作业顺序，以减少任务的延迟时间和总任务完成时间，对提高码头作业效率具有重要意义。

考虑时间窗和缓冲区容量约束，增加了卸船作业中ASC与AGV集成调度的复杂性。首先，AGV进入缓冲区顺序。每个任务的时间窗不同，当某个任务（用i 表示）要尽快完成时，AGV 在缓冲区外等待将影响i 的完成时间；若提前为i 预留缓冲位，AGV 将i 运输到缓冲区时即可堆放至缓冲位，无需等待，但预留缓冲位会增加其他AGV 在缓冲区的等待时间。再者，任务与缓冲位分配关系。AGV到达缓冲区后，除了要安排AGV进入缓冲区的顺序，还要安排任务与缓冲位的分配关系。最后，ASC 作业顺序。安排ASC 作业时需要考虑缓冲位中任务的最晚完成时间，让尽可能多的任务在规定时间窗内完成。

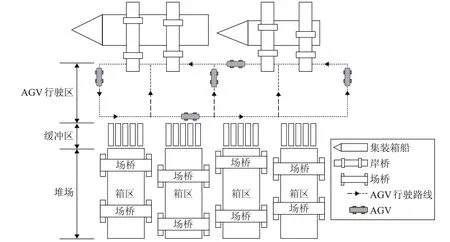
图1 集装箱码头示意图

4 模型

根据第3 章的描述，建立混合整数规划模型，模型中的集合、参数和决策变量设置如下。

集合：

R，任务的集合，R={1,2,…,r}；

R+，R+=R ⋃{ }o,d ，虚拟的起始任务和虚拟的结束任务分别为o 和d；

B，缓冲位的集合，B={1,2,…,b}。

参数：

SY，ASC完成一个任务所需要的时间；

SA，AGV在缓冲区卸载一个任务所需要的时间；

Ci，任务i 的起点至终点的距离；

V ，AGV的运行速度；

Ti，Ti=，AGV将i 从起点运输至终点所需要的时间；

变量：

tF，ASC完成所有任务的时刻；

di，任务i 的延迟时间；

yi，ASC的作业次序；

xij，当ASC 完成i 后继续作业j 时，xij=1，否则xij=0；

vib，当i 分配给缓冲位b 时，vib=1，否则vib=0；

wijb，当i 和j 堆放在缓冲位b 时，wijb=1，否则wijb=0；

uij，当i 在j 之前堆放至同一个缓冲位时，uij=1，否则uij=0。

建立混合整数规划模型如下：

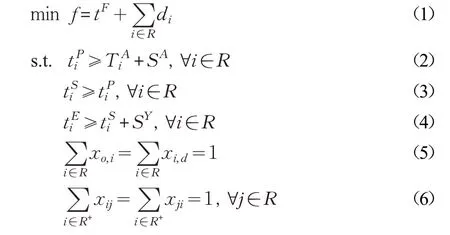
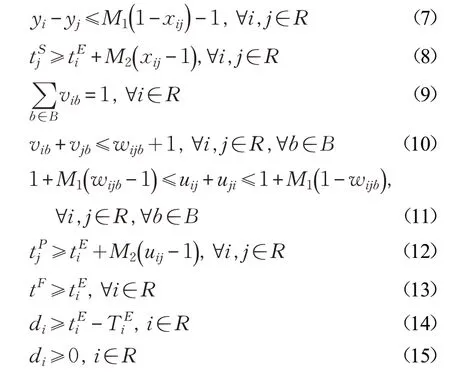
目标函数式（1）表示最小化总任务完成时间和最小化总任务延迟时间。

约束（2）～（4）为卸船过程的时刻约束。式（2）表示AGV将i 堆放至缓冲位的时刻约束；式（3）表示ASC开始作业i 的时刻不小于AGV将i 堆放至缓冲位的时刻；式（4）表示ASC完成i 的时刻约束。

约束（5）～（8）为ASC作业顺序和时刻约束。式（5）表示ASC 的第一个任务和最后一个任务分别是o 和d ；式（6）表示i 只有一个前继任务和一个后继任务；式（7）表示ASC作业两个任务的先后关系，其中M1= ||R ，|R |表示总任务数量；式（8）表示如果ASC 先作业i，紧接着作业j，则ASC 开始作业j 的时刻不小于ASC 完成i 的时刻，其中。

约束（9）～（12）为任务堆放至缓冲位的顺序和时间约束。式（9）表示每个任务都要分配给一个缓冲位；式（10）表示如果i 和j 分配到同一个缓冲位，则vib+vjb≤2，否则vib+vjb≤1；式（11）表示如果i 和j 分配到同一个缓冲位，则要么i 在j 之前堆放到缓冲位，要么j 在i 之前堆放到缓冲位；式（12）表示如果i 在j 之前堆放至同一个缓冲位，则j 堆放到缓冲位的时刻不小于ASC完成i 的时刻。

约束（13）～（15）为目标函数相关约束。式（13）表示ASC的总任务完成时间不小于ASC完成每个任务的时刻；式（14）和（15）表示i 的延迟时间约束。

5 算法求解

第4章所建立的混合整数规划模型可通过Cplex等求解器进行求解，但求解时间复杂度较高，难以在有限时间内得到理想解。根据实际调度过程可设计启发式算法在有限时间进行求解，但无法保证解的质量。遗传算法在求解优化问题过程中具有求解时间的高效性、寻优过程的自适应性和解决复杂问题的鲁棒性等特点[13]。因此，本文设计启发式算法和遗传算法进行求解。

5.1 启发式算法

根据AGV 到达缓冲区的时间先后，按顺序将AGV中的集装箱卸载至缓冲位，如果缓冲位已满，则AGV等待；然后ASC根据集装箱堆放至缓冲位的时间先后，依次作业。每个任务的完成时间用tEi表示，则总任务完成时间为，总任务延迟时间为

5.2 遗传算法

在设计遗传算法时，染色体的编码、解码、适应度计算和遗传算子（交叉、变异、选择）应该简单有效。遗传算法执行代数、交叉概率和变异概率分别记为Pgen、Pc和Pm。此外，解码方案应当体现出该问题的特征，AGV 到达缓冲区时是否可以立刻开始作业与缓冲区容量有关。遗传算法流程如下：

开始

步骤1 g ←0；

步骤2 初始化，产生初始种群P( )g（编码）；

步骤3 解码，计算P( g )的适应度值F( g )；

步骤4 While 终止条件没有满足时，do

循环开始

步骤5 交叉：由P( g )通过交叉算子产生CC( g )；

步骤6 变异：由P( g )通过变异算子产生CM( g )；

步骤7 适应度计算：计算CC( g )和CM( g )的适应度值

F( g )；

步骤8 选择：通过选择算子，从CC( g )和CM( g )中选

择下一代个体；

步骤9 g ←g+1；

循环结束

结束

5.2.1 编码

采用实数优先权编码[14]。染色体的第一段表示缓冲位与任务的分配关系，第二段表示ASC作业顺序；基因位与任务序号相对应，基因值通过U[ ]0,1 产生。以5个任务为例（如图2），第一段中，任务1 的基因值是0.43，任务5的基因值是0.27；第二段中，任务1的基因值是0.93，任务5的基因值是0.46。

5.2.2 解码

染色体的解码过程如图3。第一段的解码策略为：记染色体p 的第x 个基因位的基因值为px，当px∈[ ( b-1) /B,b/B )时，将第x 个基因对应的任务分配给缓

冲位b。通过以上计算方式，可以得到分配给缓冲位b的任务集合Rb。以B=3，R=5 为例，通过第一段的解码策略，可得到R1={2,5}，R2={1,3}，R3={4}。第二段的解码策略为：将染色体的基因值从小到大排列，得到基因值序列，排序后基因值序列对应的任务序列即为ASC 的作业顺序，记为Rsort。以R=5 为例，通过第二段的解码策略，可得到ASC 的作业顺序Rsort=4 →5 →2 →3 →1。

5.2.3 适应度计算

遗传算法进行适应度计算时，综合考虑AGV 到达缓冲区的时间、AGV进入缓冲位的顺序、缓冲位的容量和ASC的作业顺序。为方便描述，Rsort的第j 任务用k表示，则以及目标函数f 的计算过程如下。

输入：Rsort，，SA，SY，| R |，

输出：f步骤

1 j ←1

2 如果j=1，则

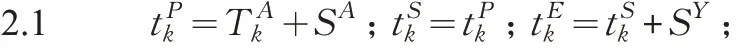
图2 编码过程

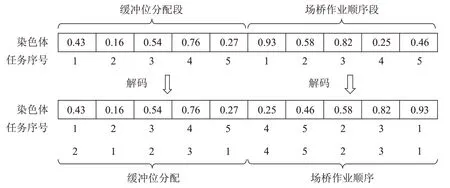
图3 解码过程

否则

2.2 如果k 到达缓冲区时，分配给k 的缓冲位b 处于空闲状态，则

否则

否则

3.2 dk=0

4 j=j+1

5 如果j ≤N ，返回步骤2；否则执行步骤6；

7 输出f

5.2.4 遗传算子

遗传算子包括交叉算子、变异算子和选择算子。

交叉算子通过模拟自然界生物的杂交过程对个体进行交叉操作，不断产生新的个体，使得遗传算法具有较强的搜索能力[15]。本文交叉算子采用两点交叉：在父代染色体群中依次选取两条染色体P1P2，随机产生两个不同的点，然后交换P1P2的值，得到两个子代染色体C1C2，如图4。

个体的适当变异可以保持种群多样性，防止陷入局部最优。本文变异算子采用均匀变异：生成一个与父代染色体长度相同的随机数向量w ，随机数范围为（0，1）。将向量w 中第x 个位置的值记为w(x)，父代染色体P 中第x 个位置的值记为P(x)，如果w(x)小于变异率pm，则生成一个范围在(0,1)之间的随机数，替代父代染色体P(x)，形成子代染色体C，如图5。

选择算子采用轮盘赌策略，操作流程如下：

开始

步骤1 i ←1

步骤2 计算种群中每个个体的适应度值f(xi,i=1,2,…,N)，N 为种群大小

步骤4 计算种群中每个个体的累计概率，染色体xi的累计概率记为

步骤5 随机生成s,s ∈[0,1]

步骤6 若k =1 且s ＜qk，则选择个体1，否则，选择个体k，使得qk-1＜s ≤qk成立

步骤7 i ←i+1

步骤8 如果i 小于等于N ，则回到步骤5；否则结束

结束

6 实验

本章对混合整数规划模型和遗传算法进行求解，其中，混合整数规划模型使用数学规划模型求解器Cplex（https：//www.cplex.com）中的分支定界法（Branch-and-Bound，B&B）进行求解。程序通过MATLAB R2018a实现，在处理器为Intel®Core™i5-8250U CPU@1.60 GHz 1.80 GHz、RAM为8 GB的电脑上运行。设置：设置成首项为0，公差为40的等差数列；=+U(0,3 600)；Ci服从U[5 00,1 500] ；SY=80 s；SA=30 s；V=5 m/s。对于GA，设置：Pc=0.9，Pm=0.3，Pgen=300。

6.1 算法性能实验

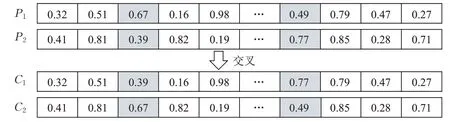
图4 两点交叉

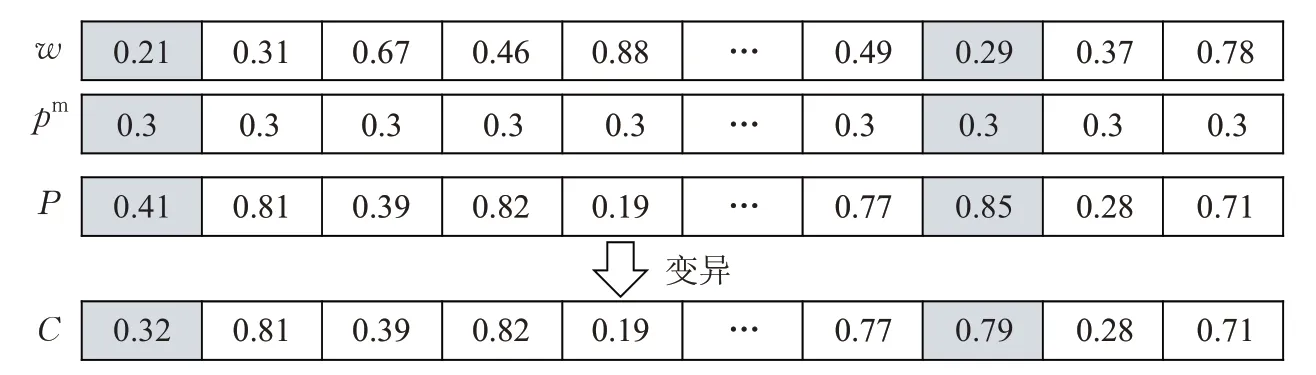
图5 均匀变异

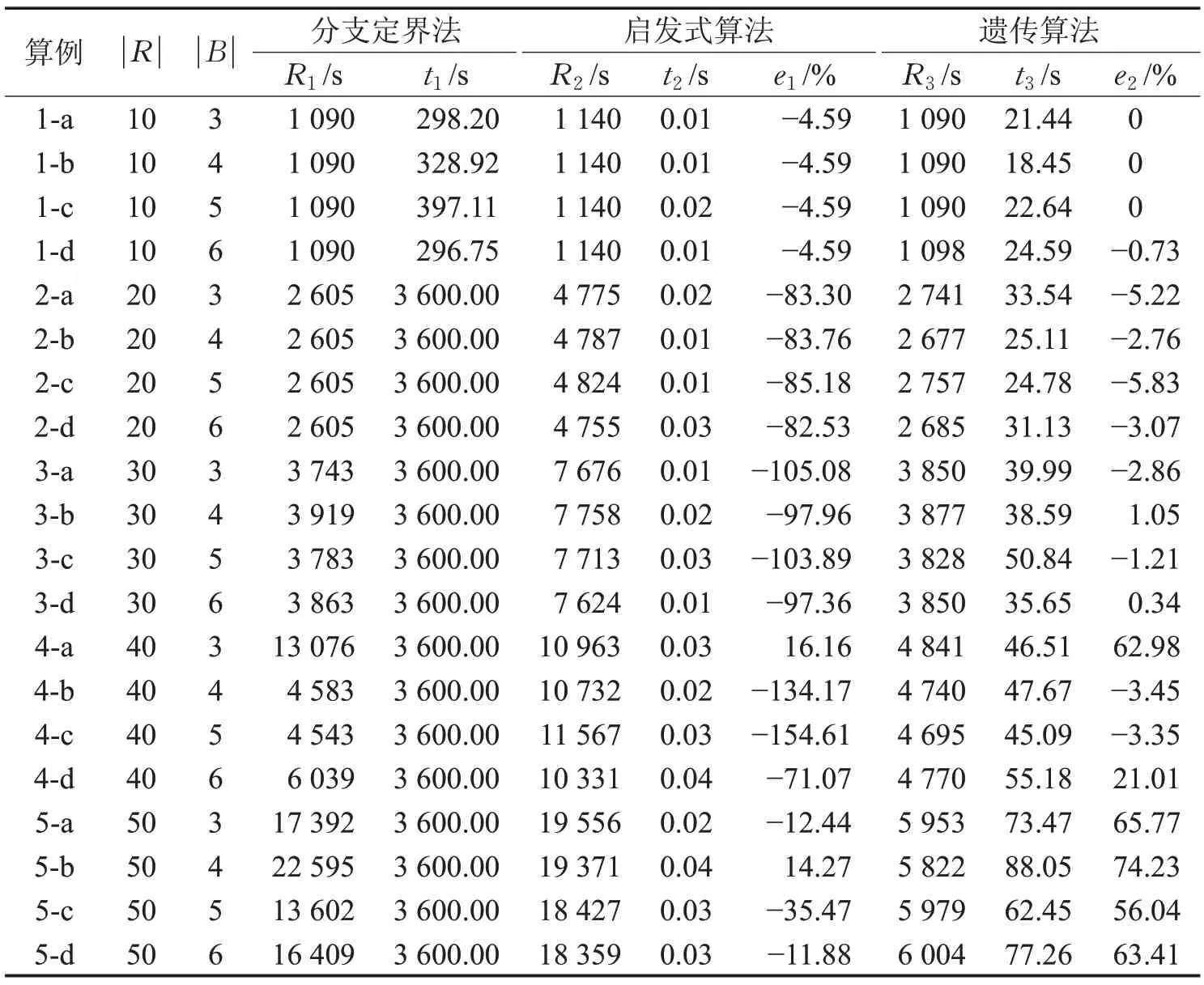
表1 分支定界法、启发式算法与遗传算法结果对比

设置5个算例集，用标号1～5表示，对应的任务数量分别为10，20，30，40，50。每个算例集设置4个子算例，用字母abcd 表示，包含的缓冲区容量分别为3，4，5，6。设置分支定界法的最大运行时间为3 600 s；遗传算法PGen=10 000，当500 代内结果无变化时GA 停止运算，记录GA 运行10 次目标函数的平均值。计算结果对比见表1。

6.2 实验结果

从表1 可看出：任务数量少于20 时，分支定界法求得的目标函数值与遗传算法基本一致；随着任务数量的增加，遗传算法的目标值逐渐优于分支定界法的目标函数值，此外，遗传算法的求解时间远少于分支定界法；启发式算法虽然能在极短时间内算出结果，但解的质量不如遗传算法。通过6.1 节的对比实验，验证了模型和遗传算法算法的有效性。

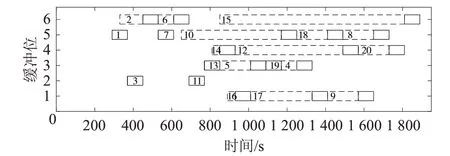
图6 ASC作业

通过GA求解算例2-d（任务数量为20，缓冲区容量为6），得到ASC 作业顺序及时间，如图6。虚线方框的长度表示任务在缓冲位的等待时间，方框中的数字表示任务序号；实线方框的长度表示ASC 完成任务所需要的时间。实线方框前没有虚线方框表示i 堆放至缓冲位时，ASC 立刻开始作业；实线方框后紧连着虚线方框表示ASC 刚完成缓冲位的任务，AGV 立刻将下一个任务堆放至缓冲位；前后两个方框之间的空白区域的长度表示缓冲位的空闲时间。

6.3 灵敏度实验

设计4个灵敏度实验，分别研究缓冲区容量对缓冲区利用率的影响、ASC 作业时间对目标值的影响、ASC作业时间对缓冲区利用率的影响和最大遗传代数对目标值的影响。采用式（16）计算缓冲区利用率，其中，表示ASC 完成任务i 的时刻，表示AGV 将i 堆放至缓冲位的时刻，tF表示ASC 完成所有任务的时刻， ||B表示缓冲位的数量。

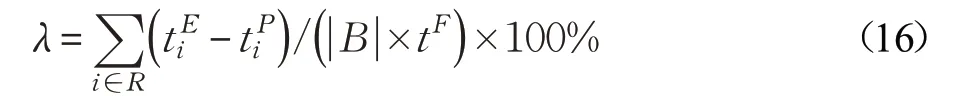
（1）缓冲区容量对缓冲区利用率的影响

设置： ||R =50， ||B 取值3，4，5，6。GA运行10次，记录目标值最小时缓冲区的利用率，如图7。从图中可看出，缓冲区容量从3 增加到4 时，缓冲区利用率从82.08%下降到74.38%；但缓冲区容量继续增加时，缓冲区利用率无明显变化。

图7 缓冲区容量对缓冲区利用率的影响

（2）ASC作业时间对目标值的影响

设置：SY取值60，65，…，95，100； ||R =50； ||B =5；记录GA 运行10 次的最小值，如图8。图中共有3 条曲线，分别对应模型中的目标函数值f 、总任务完成时间tF和总任务延迟时间。从图中可看出，ASC作业时间从60增加到90过程中，目标函数值、总任务完成时间和总任务延迟时间均缓慢增长；作业时间从90 逐渐增加到100 时，总任务完成时间缓慢增长，但目标函数值和总任务延迟时间呈指数型增长。由f=tF+可知，总任务延迟时间的快速增长引起目标函数值的快速增长。

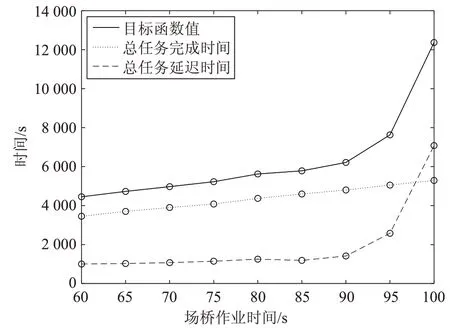
图8 ASC作业时间对目标函数的影响

（3）ASC作业时间对缓冲区利用率的影响

设置：SY取值60，65，…，95，100； ||R =50 ； ||B =5；记录GA运行10次得到的缓冲区利用率，作箱线图，如图9。箱体的上边缘表示上四分位数，下边缘表示下四分位数，中间的横线表示中位数，星号“*”表示平均值；箱体上方的短横线表示最大值，下方的短横线表示最小值；远离箱体的的加号“+”表示离群值。从图中可看出，ASC 作业时间从60 增加到100，缓冲区利用率的平均值、最小值都呈上升趋势，表示集装箱在缓冲位的停留时间增加。

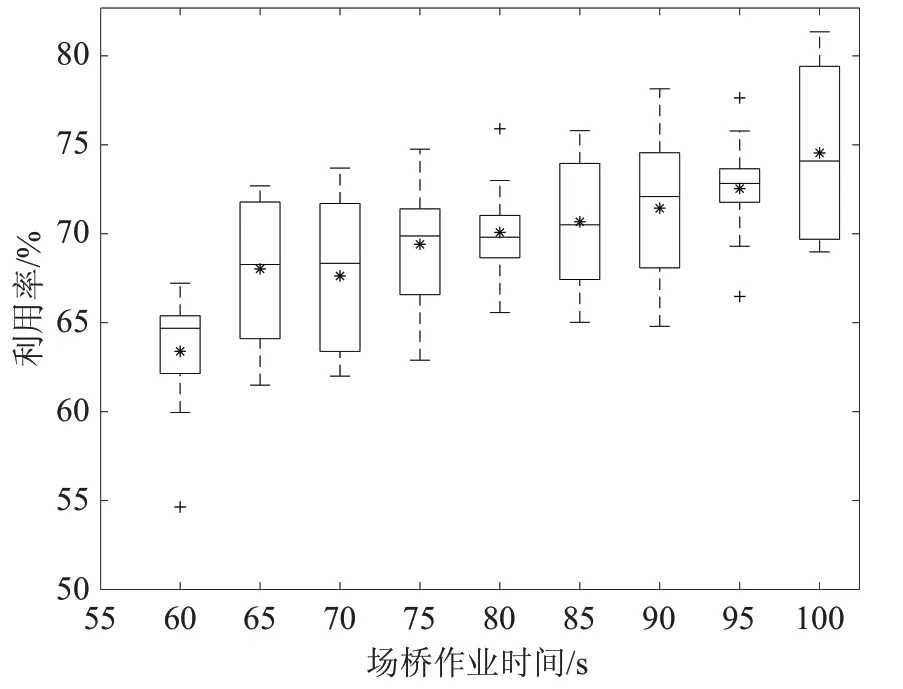
图9 ASC作业时间对缓冲区利用率的影响

（4）最大遗传代数对目标值的影响

设置： ||R =50； ||B =5；Pgen=1 000；记录GA运行10次的结果，如图10。图中共有3条曲线，分别表示GA运行10 次的最大值、最小值和其中一次运行的收敛曲线。GA迭代过程可分为三个阶段：第一阶段，目标函数值迅速下降；第二阶段，目标函数值下降速度较为平缓；第三阶段，目标函数值基本维持水平。

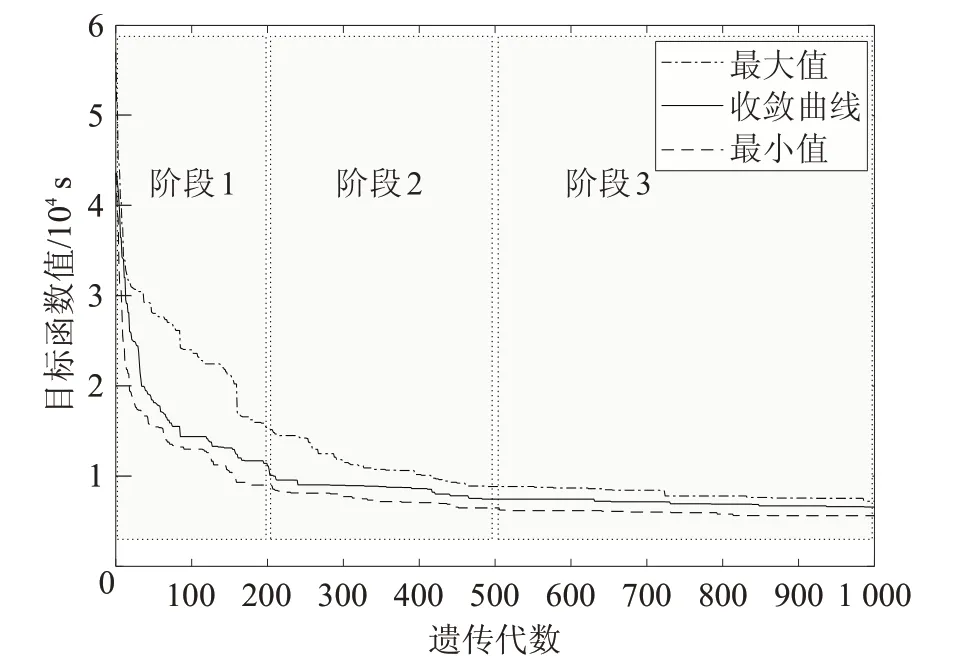
图10 遗传代数对目标函数值的影响

7 结论

本文针对ASC 与AGV 的集成调度，考虑时间窗和缓冲区容量，以最小化总任务完成时间和最小化总任务延迟时间为目标建立混合整数规划模型，采用分支定界法和遗传算法进行求解，确定任务与缓冲位的分配关系以及ASC的作业顺序。通过设置不同任务数量的算例集进行算法性能实验，验证了模型和算法的有效性。通过灵敏度分析表明，ASC 作业时间大于90 s 时，增加ASC作业时间将使得总任务延迟时间呈指数式增长，进而引起目标函数值的迅速增加。