针对不平衡数据的过采样和随机森林改进算法
2020-06-09张家伟郭林明杨晓梅
张家伟,郭林明,杨晓梅
四川大学 电气工程学院,成都610000
1 引言
目前,对于二分类问题,机器学习方法大多基于正负样本的比例相近这一假设建立分类模型[1],而在实际应用中,通常会出现数据不平衡现象,这种不平衡常会给分类器的实用性带来很大的影响,如医疗领域的肿瘤诊断,假设肿瘤诊断数据集中有100 样本,其中99 个正样本(良性肿瘤),1个负样本(恶性肿瘤),分类器经过训练后,把这100个样本都分为了正类,准确率为99%,然而被误分的这个负样本却可能影响诊断结果。因此,当遇到数据不平衡问题时,以总体分类准确率为学习目标的传统分类算法会过多地关注多数类,从而使得少数类样本的分类性能下降,难以获得有效的分类模型。
国内外现有对数据不平衡问题的解决方法一般有三类:数据预处理、代价敏感学习、集成学习分类[2-3]。数据预处理分为过采样和欠采样,过采样利用少类样本生成新样本来提升少数类样本数量,应用最为广泛的是SMOTE[4],SMOTE在每个少数类样本与其K 个近邻样本之间的连线上产生合成新样本。然而SMOTE没有对每个样本进行区别选择,这会导致生成冗余样本。针对文献[4],文献[5-6]使用聚类、最近邻的方法改变用于合成新样本的中心样本,一定程度避免了生成样本的冗余现象。欠采样通过舍弃多数类样本来平衡数据集,如文献[7-8],虽然保留下来的样本相对具有代表性,但依然有可能丢弃对分类有用的样本。代价敏感学习在分类算法中引入代价函数,通过最小化错分代价构造分类器,如文献[9-10]通过数据的非平衡系数和决策树的分类准确度给决策树加权,增加模型对少数类样本判错的代价,提升少数类样本分类正确率。集成学习分类把性能较低的多种弱学习器通过适当组合形成高性能的强学习器,如文献[11-12]将Adaboost 与过采样和欠采样结合,提出SMOTEBoost 和RUSBoost 算法,使分类器有更强的鲁棒性,提高了分类器准确率。文献[13]使用欠采样和随机森林算法根据气象参数预测PM2.5浓度,获得了较好的预测精度,文献[14-17]使用随机森林(Random Forest,RF)算法在多种不平衡数据分类场景和其他工程领域应用中取得了良好的效果,模型泛化能力强。
然而这些方法容易出现两个方面的问题,数据预处理层面,欠采样可能会丢弃对分类器很重要的有价值的潜在信息[18],经典的过采样SMOTE 算法每个样本合成相同数量的新样本,没有充分利用那些更具有类别代表性样本,可能会产生冗余数据。算法层面,随机森林算法在分类问题方面已经得到了广泛的应用,但是,受样本不平衡影响,在训练阶段随机选取训练集时会加剧训练样本的不平衡度,其次,每棵决策树在投票时权重都相等,但受训练时的数据影响每棵决策树的分类效果不同,总会有一些训练效果不高的决策树投出错误的票数,从而影响随机森林的分类能力。
为了解决上述问题,本文提出了加权过采样和加权随机森林算法。加权过采样策略根据每个少数类样本相对于剩余少数类样本的欧式距离给每个样本分配不同的权重,利用SMOTE算法合成新样本过程中,每个少数类样本生成新样本的数量根据其权重变化,从而增加更有类别代表性样本合成数量。加权随机森林根据Kappa系数评价决策树训练效果,给每棵树分配不同的权重,每棵决策树在进行投票时,通过权重的设置,提高分类效果好的决策树的投票话语权,降低效果差的决策树对结果的影响。加权过采样和加权随机森林结合使用能够进一步提升算法的分类效果。
2 加权过采样
经典的过采样SMOTE 算法中,每个少数类样本生成的新样本数量是相同的,这会产生很多对类别区分价值不大的样本,从而影响之后的分类器训练效果。因为并不是每个样本对类别区分的价值都一样,离类别中心越近的样本更能代表本类特征,离边界越近的样本能够更好地区分不同类别的界限,这两种样本包含更多的分类信息,对分类的价值更大,希望能够充分利用样本与类别中心和边界的距离,在SMOTE 算法中让靠近类别中心和边界的样本生成新样本数量更多。对此,使用每个少数类样本相对于剩余少数类样本的欧式距离确定每个样本的相对位置,为每个样本分配不同的权重。使靠近类别中心和类别边界的样本拥有更大的权重,在生成新样本时,每个样本根据权重确定生成数量,权重越大,生成数量越多。
2.1 权重计算步骤
设训练集的一个少数类的样本数为M ,每个样本包含C 个特征。
(1)计算每个样本到其他样本间的欧氏距离,如式(1)所示:

式中,i=1,2,…,M ,j=1,2,…,M ,i ≠j,Di,j( xi,xj)表示第i 和j 两个样本间欧式距离。
(2)计算样本xi到其他样本距离之和Di,Di越大表示xi越靠近边界,Di越小表示xi越靠近中心,如式(2)所示:

(3)对Di进行归一化,如式(3)所示:
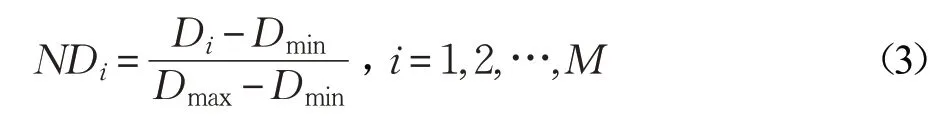
(4)计算RNDi,即为ND 中各元素与ND 均值之差的绝对值,RNDi越大则表示该样本越靠近类别中心或者类别边界,样本价值越高,对分类更有效,它所生成的新样本数量就应该越多,如式(4)所示:

(5)计算每个样本的权重,如式(5)所示:

Wi为第i 个样本的权重值。需要生成新样本的数量乘以此权重即为最终该样本生成新样本的数量。
表1展示了新样本生成数量随权重变化的特点,假设某少数类有5 个样本A、B、C、D、E,需要生成的新样本总数为25,那么传统SMOTE方法中每个样本都会生成5 个新样本,为简化计算,给每个样本到其他样本距离之和D 随机赋值,如表1 中所示,经过权重计算步骤后,每个样本的生成数量不一样,靠近中心和边界的样本生成数量更多。

表1 权重计算示意
2.2 加权SMOTE算法步骤
设加权SMOTE 算法将为训练集的少数类合成N个新样本,N 是正整数。
(1)对于该少数类中第i 个样本xi,计算它到该类其他所有样本间的欧式距离,得到其k 个近邻样本。
(2)对于第i 个样本xi,从其k 个近邻样本中随机选取个样本为向下取整。
(3)在(2)中选取的Nw个样本中,根据公式(6)生成Nw个关于少数样本xi的新样本。
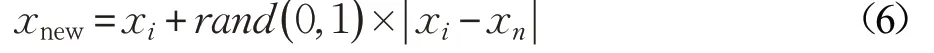
其中,rand( )0,1 是0 和1 之间的随机数。SMOTE 和加权SMOTE示意图如图1所示。
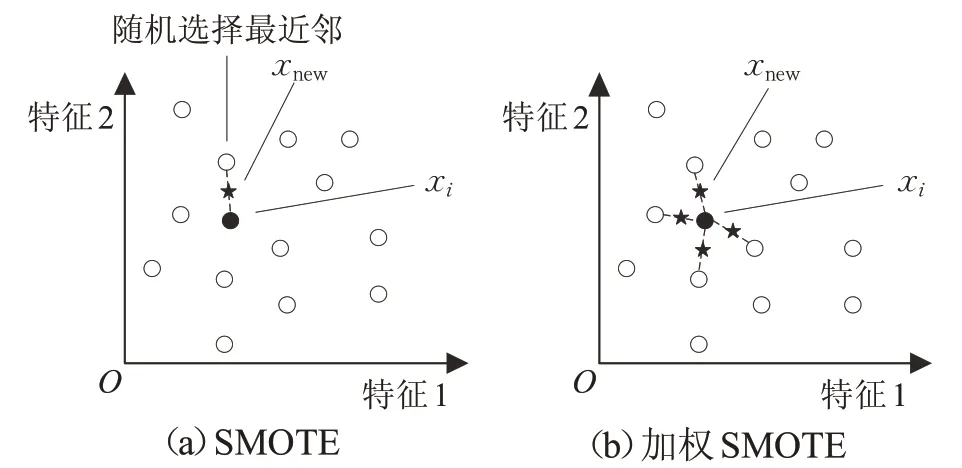
图1 SMOTE和加权SMOTE示意图
3 加权随机森林
3.1 随机森林算法
随机森林算法是Breiman L[19-21]提出的一种分类算法,它是一种集成机器学习方法,实质是将Bagging算法和random subspace算法结合起来构建了一个由多棵互不相关的决策树组成的分类器,它改善了决策树容易发生过拟合现象的缺点[22],训练样本采用自助法重采样(Bootstrap)技术,从原始数据集中有放回重复随机抽取N 个样本作为一棵树的训练集,每次随机选择训练样本特征中的一部分构建决策树,每棵决策树训练生长过程中不进行剪枝,最后采用投票的方式决定分类器最终的结果。例如,对一个训练好的随机森林模型,测试集为X,类别数为C,决策树数量为T,则模型的输出为:
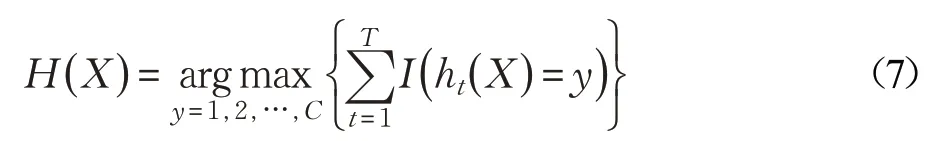
其中,ht( X )为第t 棵决策树的输出,I(⋅)是一个指示函数,函数中参数为真时,函数值等于1,否则等于0。
3.2 加权随机森林算法
由公式(7)可知,每棵决策树在投票时权重都相等,但是由于每棵树训练集不同,又互相独立训练,所以决策树的分类精度会不同,加之受到样本类别不平衡的影响,会进一步影响决策树的分类效果,使得一些效果不好的树投出错误的票数,从而影响随机森林的分类能力。为此本文提出了加权随机森林模型,主要方法是在决策树训练阶段,评估决策树的分类效果,并给每棵树赋予一个权重,在随机森林算法投票时,每棵树都要乘对应的权重值,这样可以降低训练精度不高的决策树对整个模型的影响。因此,公式(7)中的模型输出改写为:

其中wt为第t 棵决策树的权重值。
从原始训练集中有放回地随机抽取样本作为每棵树的训练集,抽取数量等于原始训练集样本数量,由于是有放回抽样,会有部分样本未被抽中,这部分被称为袋外样本[23],数量通常为原始样本数量的三分之一,利用袋外样本作为每棵树的测试集来评估分类性能,并据此赋予该决策树相应的权重,使分类性能更好的决策树拥有更大的权重。
对于使用不平衡数据的分类器,常用的分类精确度这个评价指标无法很好地衡量分类能力,因为它只考虑了被正确分类样本的情况,认为多数类和少数类的分类错误同样重要[24]。因此,使用Kappa 系数(Kappa Coefficient,CK)来评价决策树整体分类能力,CK 是1960年Cohen等人提出用于评价判断的一致性程度的指标,它同时考虑了各种漏分和错分样本,代表着分类与完全随机的分类产生错误减少的比例,其计算结果为(-1,1),但通常情况下CK 是落在(0,1),CK 值越大说明预测结果和实际结果一致性越高,分类器性能越好[25]。CK计算如式(9)所示:

其中,ACC(accuracy)为分类精确度,表示分类的实际一致性比率,CKc为分类的偶然一致性比率。 ACC 和CKc通过表2所示的混淆矩阵[26]计算得到。
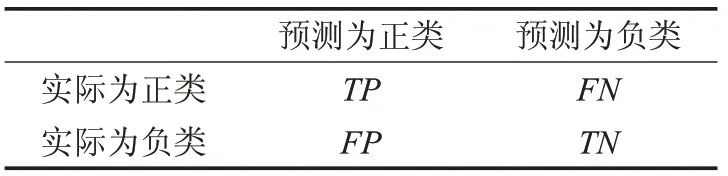
表2 二分类混淆矩阵
混淆矩阵中,TP(True Positive)表示实际是正类,预测也是正类的样本数。FN(False Negative)表示实际是正类,预测是负类的样本数。FP(False Positive)表示实际是负类,预测为正类的样本数。TN(True Negative)表示实际是负类,预测为负类的样本数。

为了把更大的权重分配给更有能力的分类器,文献[27]研究表明:若一组独立的分类器L1,L2,…,LM相互独立,精确度为p1,p2,…,pM,那么每个分类器权重和对应精确度关系如公式(12)所示:
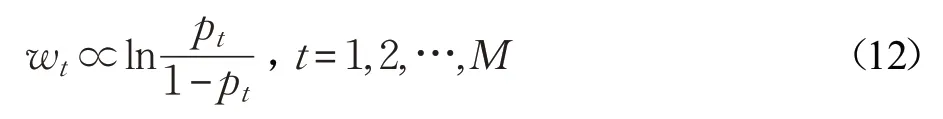
用CK 替换公式(12)中的pt,由于CK 的取值范围为(-1,1),将公式(12)改写为公式(13):
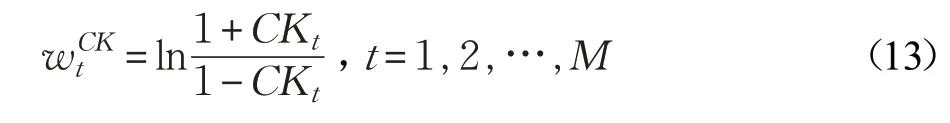
根据公式(14),决策树的CK 值越高,则其分配的权重也越大,对最终投票的结果影响也更大。CK 和权重W的关系如图2 所示。将公式(13)带入公式(8),就能得到随机森林分类器最终的输出结果。

图2 CK 和权重W 关系图
整体算法流程如图3所示,从数据预处理和算法两个层面进行改进,数据预处理阶段进行过采样时,通过少数类样本在类内的距离分布区分其对分类的重要程度,给每个样本加权,减少生成冗余样本,从数据层面提高训练集的质量,使后续分类算法在训练阶段能够获得更多有效的少数类样本信息,从而提高算法对少数类样本的分类正确率,根据混淆矩阵与第4章的评价指标计算公式可知,少数类样本分类正确率的提高又能提升整体分类性能。算法改进阶段通过CK评价每棵决策树整体分类效果,并根据CK给每棵决策树分配投票权重,减少分类效果不好的决策树对结果的影响,使算法的输出结果更加合理,提高对数据集的整体分类性能。因此,这两个层面的加权改进是有必要的。

图3 算法流程图
4 实验
4.1 数据集
为了验证改进算法的有效性,从KEEL[28]数据集仓库中选取了5个非平衡二分类数据,这些数据的信息如表3所示。
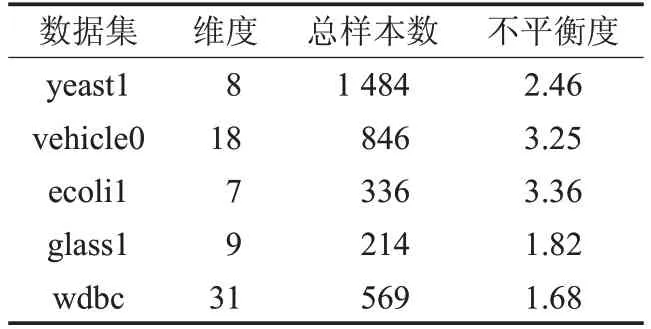
表3 实验数据集
4.2 评价指标
对于不平衡数据集,分类精度无法全面地评估分类效果,采用特异度(specificity)、CK、G-mean 进行评价,特异度用来评价少数类样本分类的正确率。CK 和Gmean 用来评价不平衡数据集整体分类性能,G-mean 表示少数类分类精度和多数类分类精度的几何平均值,是保持多数类、少数类分类精度平衡的情况下最大化两类的精度。


4.3 实验结果
将SMOTE(SM)、加权SMOTE(WSM)、随机森林(RF)、加权随机森林(WRF)不同组合形成的算法,即SM+RF、WSM+RF、SM+WRF与本文算法(WSM+WRF)进行对比,实验这4 种算法在vehicle0 数据集上的分类结果。数据集中多数类样本和少数类样本分别取70%作为训练集,30%作为测试集,随机森林算法中两个常用参数为决策树的数量(ntree)和随机选择特征的数量(mtry),随着ntree 的增加,随机森林分类误差会趋于稳定,由于随机森林具有不会过拟合性,将ntree 设置足够大。mtry 用来协调分类性能和多样性之间的平衡[29],将mtry 设置为特征总数的平方根。
图4 和图5 为在vehicle0 数据集上四种算法组合的特异度和G-mean 对比结果。由图可知,随机森林算法中决策树数量增加到100 棵左右时,specificity 和Gmean 趋于稳定。在这两个指标的表现上,WSM+RF 算法优于SM+RF算法,WSM+WRF算法优于WSM+RF算法,SM+WRF 算法优于WSM+RF,结果表明,都使用随机森林分类器的情况下,加权SMOTE 比SMOTE 对不平衡数据的处理更有效,经过训练后,能够使更多的少数类样本得到正确的区分,有助于提高分类器整体分类能力。都使用加权SMOTE 处理数据的情况下,加权随机森林比随机森林的分类能力更好。
为了进一步验证加权SMOTE和加权随机森林对分类结果的影响,用未过采样Ori+RF、Ori+WRF、SM+RF、WSM+RF、SM+WRF 与本文算法在更多数据集上进行实验,分类结果取决策树数量大于100 后的稳定值,结果如表4所示,可以看出,WSM、WRF与Ori和RF相比,都能提升分类结果的specificity,使少数类的分类正确率得到提高。通过表4中Ori+RF和Ori+WRF的结果可以看出,WRF对数据集的整体的分类效果提升明显,每个数据集的CK 和G-mean 均有提升,与未改进算法相比,CK 最高提升了3.75%,G-mean 最高提升了2.56%。通过表4、表5中Ori+RF、SM+RF、WSM+RF结果可以看出,SM的CK和G-mean高于Ori,WSM的CK和G-mean又高于SM,因此,WSM对数据集的整体分类效果也有提升。vehicle0使用WSM+RF算法的CK高于SM+WRF,ecoli1使用WSM+RF算法的CK和G-mean高于SM+WRF,glass1和wdbc使用WSM+RF算法的CK和G-mean低于SM+WRF,这是因为vehicle0 和ecoli1 数据集的不平衡度比glass1和wdbc高,WSM从数据层面的改进比WRF从算法层面的改进对分类效果的提升更明显。本文算法结合WSM和WRF对不平衡数据集的整体分类效果最好。

图4 vehicle0数据集specificity对比图
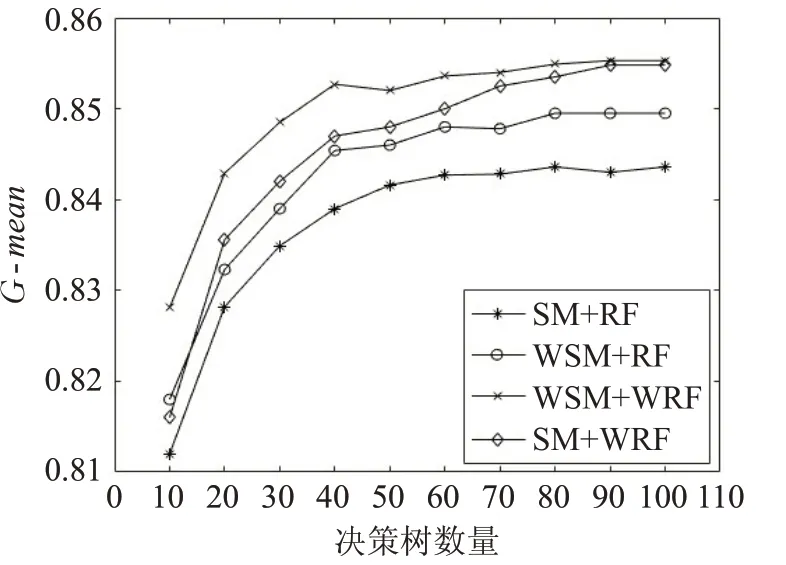
图5 vehicle0数据集G-mean对比图

表4 不同数据集上不同算法与本文算法分类结果对比

表5 本文算法与其他算法分类结果对比
4.4 与其他算法比较
为验证本文提出的加权SMOTE和加权随机森林算法的有效性,与SMOTEBoost、RUSBoost算法进行对比,如表5所示,可以看出,本文WSM+WRF算法在yeast1、vehicle0、glass1、wdbc 数据集上的G-mean 和CK 比其他两个算法都有明显的提升,wdbc 数据集上G-mean低于SMOTEBoost算法,但CK 依然比其他两个算法高。
5 总结与展望
针对数据不平衡对分类器分类性能影响的问题,本文在原有的算法基础上从数据层面和算法层面提出了两种改进,数据层面提出加权SMOTE算法,根据少数类样本间的相对欧式距离生成更多有价值的少数类样本,提升分类器训练效果,算法层面提出加权随机森林算法,给分类效果更好的决策树分配更高的投票权重,从而提升随机森林算法的分类准确性,通过在一系列数据集上的实验表明,加权SMOTE 和加权随机森林算法可以提升少数类样本分类准确率,对不平衡数据集的整体分类效果有显著的优化。但本文改进算法也存在一定的局限性,对不平衡度较高和特征维度较高的数据集分类效果提升不明显,这是因为在特征维度较高时,欧式距离并不能很好地衡量样本的空间分布,不平衡度较高时,少数类样本数量相对较少,类别边界和中心不明显,这些会影响到加权SMOTE的权重分配,产生冗余样本,从而影响分类效果。虽然并不是在所有数据集上都能够取得显著的效果,但本文提出的算法为处理数据不平衡分类问题提供了一种可选择参考的思路。在今后的工作中,会对不同类型的不平衡数据集分类问题进行更加深入的研究。
