层适应网格上求解奇异摄动问题的粒子群算法
2020-06-09程立正
周 琴,程立正
1.湖南涉外经济学院 信息与机电工程学院,长沙410205
2.湖南师范大学 计算与随机数学教育部重点实验室,数学与统计学院,长沙410081
1 引言
近年来,在科学技术和工程领域中经常面临求解一些带小参数的奇异摄动问题。如为了开采石油、天然气等资源需要研究地下多孔介质中的渗流问题;为预报天气状况需要求解描述大气运动的流体力学和热力学方程组等等。奇异摄动问题描述的现象往往在局部区域具有奇异性,它的解含有边界层或内层,解或其导数在此区域内变化非常剧烈。它的解除与变量有关外,还与摄动小参数有关。
若在均匀网格上利用数值方法求解奇异摄动问题,为了达到一定的计算精度,局部的奇异性会导致求解区域上的网格过细,造成不必要的计算时间和数据存储上的浪费。并且均匀网格下求解在解的急剧变化区域会产生非物理振荡,得到不满意的结果。层适应网格[1-3]是能有效求解奇异摄动问题的一种非均匀网格,包括Shishkin 网格、Bakhvalov 网格、Bakhvalov-Shishkin 网格等,该类网格具有在边界层局部加密的特性。学者们在层适应网格上研究各类奇异摄动问题,已取得一些研究成果,如文献[4-12]。在层适应网格的构造中,需要选择网格过渡点来确定网格分布。因此,如何选取网格过渡点中的参数,使得数值解能更好地逼近精确解,是非常有意义的一项工作。文献[13]对一类奇异摄动问题,采用差分进化算法优化参数进行了求解。文献[14]对一类含两个参数的奇异摄动问题,采用差分进化算法在Shishkin网格上进行了求解。
粒子群算法(PSO)是由Kennedy J和Eberhart R C[15-16]于1995 年共同提出的一种优化算法。它从随机解出发,通过迭代寻找最优解,通过适应度来评价解的品质。目前粒子群算法已广泛应用于函数优化、神经网络训练、模糊系统控制等领域。如文献[17]提出一种基于陀螺仪传感器结合改进粒子群算法,解决了传统3D 建模技术测量不精确的缺陷。文献[18]针对神经网络权值选取不精确的问题,提出改进的粒子群优化算法结合神经网络动态选取权值的方法。文献[19]研究了改进的粒子群优化算法在无约束优化问题中的应用。文献[20]将拟合方法与粒子群算法相结合,提出一种新的混合型粒子群优化算法,用于方程参数估计,得到了较好的结果。
本文研究一类奇异摄动对流扩散问题:

其中,ε 是一个极小的正参数,满足0 <ε ≪1。假设函数a(x),b(x),f(x)充分光滑,且存在常数α 使得a(x)≥2α >0,b(x)≥0。这类奇异摄动问题的解在右边界层变化剧烈。将对该类奇异摄动问题构造Bakhvalov-Shishkin网格,采用粒子群算法对网格参数α 进行优化,使得所求数值解的误差范数达到最优。
2 Bakhvalov-Shishkin网格上的差分格式
设网格剖分数N 为偶数,网格节点为{xi}(i=0,1,…,N),定义网格过渡点, Bakhvalov-Shishkin 网格(简记为B-S 网格)的构造为将求解区间[0,1]分解为两个子区间[0,1-τ]和[1-τ,1],再将子区间[0,1-τ]作等分,将子区间[1-τ,1]也分为份,但要使得exp(-α(1-x)/ε)等分布在网格节点xi(i=N/2,N/2+1,…,N)上,得到如下网格分布[12]:
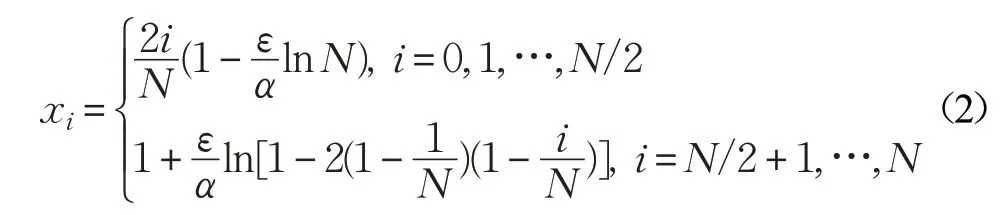
显然,当小参数ε 和网格剖分数N 确定时,网格过渡点τ 由参数α 决定。选取不同的参数α 会使得网格点发生变化,从而影响求解的精度。
在式(2)定义的B-S网格{xi}(i=0,1,…,N)上,记uNi为xi处对应的数值解,可构造问题(1)的迎风差分格式如下:
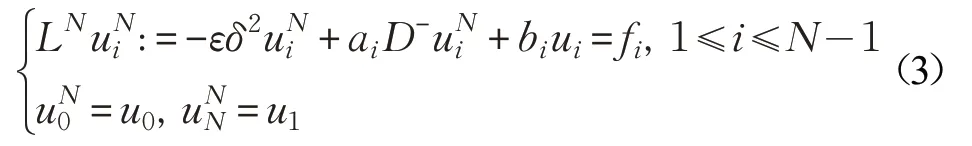
文献[12]证明了在B-S网格(2)上利用差分格式(3)求解奇异摄动问题(1)的数值解一致一阶收敛于真解,即:
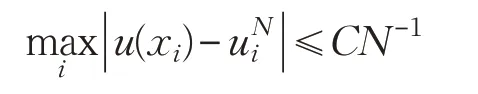
其中,u(xi)和分别为网格点xi处对应的精确解与数值解。
3 优化网格参数的粒子群算法
记uN为当网格剖分为N 个子区间时在B-S网格(2)上求解奇异摄动问题(1)的数值解,它可视为网格参数α 的函数uN(α)。由于很多实际问题中很难得到奇异摄动问题的精确解,因此使用双重网格的数值解来估计数值解误差,记:

其中,u2N(α)为将网格剖分为2N 个子区间时的数值解,此时的网格点由网格剖分为N 个子区间时的B-S网格点及相邻网格的中点组成。
为了使误差尽可能得小,构造如下的目标函数:

以误差范数(4)为目标函数寻找最优的网格参数α。
粒子群算法将参数α 初始化为一群随机粒子,通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个最优解来更新自己。第一个是粒子本身所找到的最优解,即个体最优解,记为pbest 。另一个是整个种群目前找到的最优解,即全局最优解,记为gbest 。记Vt和xt分别为第t 次迭代前粒子的速度和位置,粒子根据如下的公式来更新速度和位置:
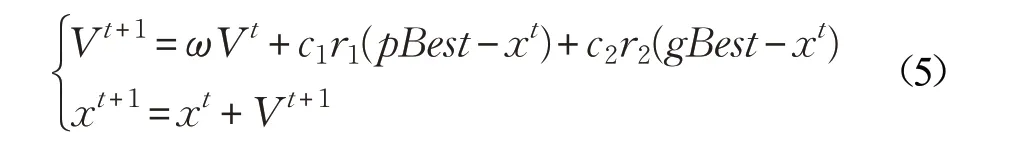
其中,ω 为惯性权重,r1,r2是区间(0,1)的随机数,c1,c2是学习因子。
下面给出采用粒子群算法结合迎风差分格式在Bakhvalov-Shishkin网格上求解奇异摄动对流扩散问题(1)的算法步骤:
步骤1 对参数α 进行种群随机初始化,由式(2)得到对应的B-S网格。此时迭代次数k=0。
步骤2 利用追赶法等对B-S网格上的差分格式(3)进行求解,得到B-S 网格上N+1 个网格点上的数值解uN(α)。在原B-S 网格上添加相邻网格点的中点,得到2N+1个网格点,再求解差分格式(3),得到数值解u2N(α),进而计算出每个粒子对应的目标函数(4)的适应值。
步骤3 对每个粒子α,将其当前适应值与其个体历史最佳位置(pbest)对应的适应值做比较,如果当前的适应值更优,则将用当前位置更新历史最佳位置pbest。
步骤4 对每个粒子α,将其当前适应值与全局最佳位置(gbest)对应的适应值做比较,如果当前的适应值更高,则将用当前粒子的位置更新全局最佳位置gbest。
步骤5 利用式(5)更新粒子α 的速度和位置。由α的新位置,计算对应的Bakhvalov-Shishkin网格。
步骤6 若迭代次数k 小于设定的最大迭代次数Gmax,转步骤2,并令k=k+1。否则,停止迭代,得到最优网格参数α 及最优误差范数。
4 数值实验与结果分析
奇异摄动对流扩散问题(1)中,ε 是扩散项系数,a(x)是对流项系数,当ε 极小时,该问题为稳态的对流占优问题,可以用来描述稳态的热传导、粒子扩散、化学反应等现象。下面选择一个变系数算例和一个常系数算例进行数值模拟。
4.1 变系数奇异摄动问题
考虑奇异摄动问题:

根据上章给出的算法步骤,采用粒子群算法在B-S网格上对该问题进行数值实验。实验时取种群规模为50,最大迭代次数Gmax为50 次,惯性权重ω=0.8,学习因子c1=c2=1。参数α 需要满足的条件为a(x)≥2α >0,其中a(x)是问题中u'(x)项的系数,故此例中参数α 取值范围应满足。若α 过小,网格分布(2)中右边界层集中的网格点越少,不利于反映解的性质,故在实验时取粒子α 的搜索范围为[0.05,0.25]。
4.2 常系数奇异摄动问题
考虑奇异摄动问题:

此例中u'(x) 项的系数为2,网格参数α 应满足条件0 <2α ≤2,实验时取参数α 的搜索范围为[0.1,1],其他实验参数的选择同上例。
4.3 实验结果及分析
针对两个算例,取网格剖分数N =32,64,128,256,小参数ε=10-2,10-3,10-4,10-5,10-6进行实验。表1 和表2分别列出了以式(4)为目标函数时,算例1和算例2中粒子群算法计算出的最优网格参数及目标函数值。可见在目标函数最优时,误差仍保持收敛性。
图1作出了两个算例中N=32 ε=10-4时,随着迭代次数增加目标函数的变化。可见经过10次左右的迭代,目标函数可接近最优值。针对两个算例的求解,粒子群算法具有较快的收敛速度。
将参数α 取两个固定值(分别为搜索范围的上限和下限)与α 取粒子最优解时的误差范数目标函数(4)作比较,发现误差的区别主要体现在x=1 附近的边界层。问题的解在x=1 附近的边界层变化剧烈,为了便于观察边界层误差情况,图2、图3分别作出了两个算例中ε=10-4时参数α 取粒子最优解与固定值的边界层误差曲线对比,图(a)和图(b)分别为网格剖分数N=32 和N=64 的情况。

表1 算例1中粒子群算法计算出的最优网格参数及目标函数值
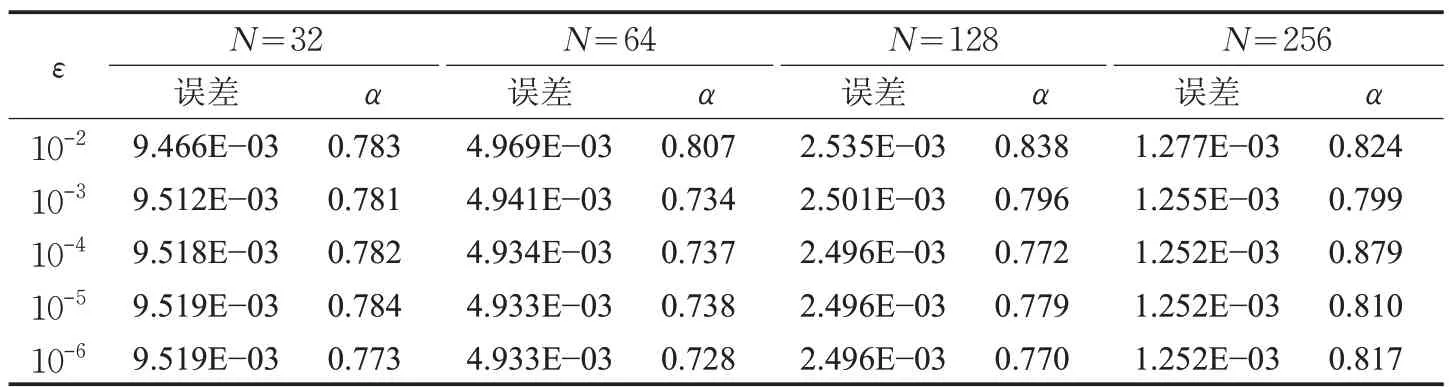
表2 算例2中粒子群算法计算出的最优网格参数及目标函数值
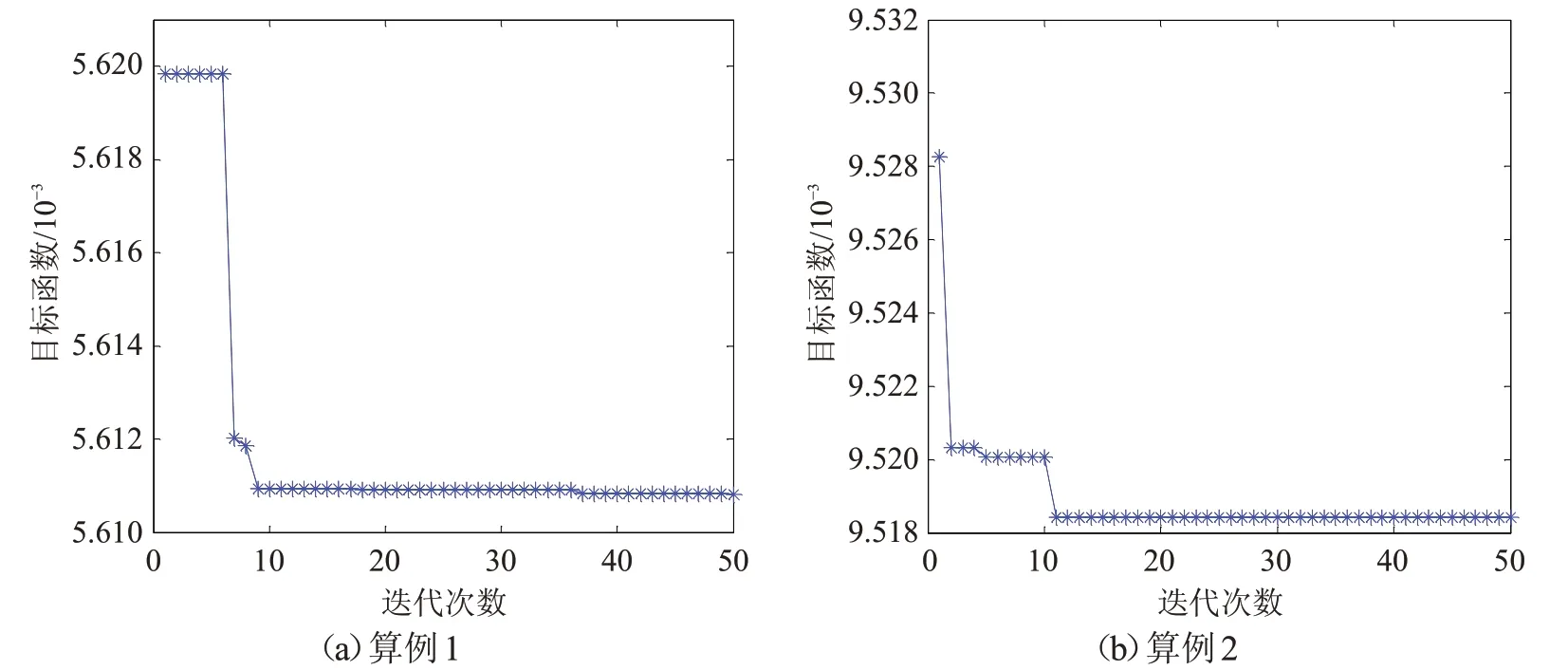
图1 N=32,ε=10-4 时的迭代曲线

图2 算例1中ε=10-4 时粒子最优解与固定值的边界层误差曲线对比

图3 算例2中ε=10-4 时粒子最优解与固定值的边界层误差曲线对比
表3、表4 分别列出了算例1 中ε=10-2和ε=10-4时,采用粒子群算法选取网格参数和取参数α 为固定值0.05 和0.25 时的误差。表5、表6 分别列出了算例2 中ε=10-2和ε=10-4时,采用粒子群算法选取网格参数和取参数α 为固定值0.1和1时的误差。

表3 算例1中ε=10-2 时的误差比较
误差曲线和表中数据均反映出采用粒子群算法确定的最优参数α 对应的误差明显优于α 取固定值时的误差。特别是与α 取粒子搜索下限相比,采用粒子群算法得到的数值解精度要高出许多。因此,与人为选择B-S网格中的网格参数相比,利用粒子群算法优化选择网格参数进而求解奇异摄动问题能得到较好的数值结果,特别是边界层的数值解精度能得到较大提高。

表4 算例1中ε=10-4 时的误差比较

表5 算例2中ε=10-2 时的误差比较
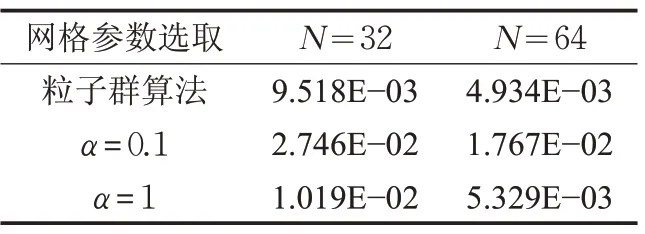
表6 算例2中ε=10-4 时的误差比较
5 结束语
本文采用粒子群算法优化选择网格参数,提出了在Bakhvalov-Shishkin网格上求解一类奇异摄动问题的粒子群算法。实验结果表明,与选择固定的网格参数相比,采用粒子群算法计算能得到更好的计算精度,并且数值结果具有收敛性。本文提到的方法也可以推广到高维问题的计算中。
