带等级约束的多重工件在线(半在线)排序问题*
2020-06-09代兵飞夏玉霞
代兵飞 夏玉霞
(云南大学数学与统计学院 昆明 650000)
1 引言
排序问题是一类具有广泛应用的组合最优化问题,其目标是寻找一个使机器的最大完工时间最小的调度。等级约束常常发生在服务业,服务者将客户划分成不同的等级。等级越高的客户享受越好的服务,区分不同服务的方法是给服务者(如:机器)和客户(如:工件)贴上带有服务等级的标签,并且服务者只为服务等级不低于自己的客户提供服务。
对于经典的在线排序问题,最早由Bar-Noy 等人提出并研究。当机器台数m=2 时,Xu 和Liu 在文献[1]中对工件带准备时间的调度问题给出了一个竞争比为1.555 的在线算法。Jiang 等和Park 等人在文献[2]和[3]中设计了竞争比都为5/3的最优在线算法。Zhang 和Tan 在文献[4]中对工件可在机器间任意分割且可并行加工的在线排序问题设计了基于线性规划解的在线算法,证明了当m≥2时,此算法的竞争比为γm,这里γm是线性规划目标函数的最优值。当机器台数m>2 且为固定常数时,文献[5]、文献[6]中所给在线算法的竞争比都大于2。
当机器台数m=2 时,存在多个半在线算法[7~9]。当已知工件加工时间总和而且每个工件的加工时间被界定于[1,α](1 ≤α<2)时,Luo和Xu在文献[7]中证明了半在线算法的竞争比:当 1 ≤α< 2 时,竞争比为 (1+α)/2 ;当α≥2 时,竞争比为3/2。当已知工件的加工时间总和时,Park 等在文献[3]中也设计了一个竞争比为3/2的最优半在线算法。在文献[8]中,当已知离线最优值和工件的最大加工时间时,Wu 等分别设计了一个竞争比为3/2 的半在线算法和一个竞争比为( 5+1)/2 的半在线算法。
在经典的在线和半在线排序中,工件总是一个接一个地到达。但在许多环境中,例如高性能计算(请参阅文献[9~10]),每个用户总是提交一些要处理的相同任务。对于不同物品类型的装箱问题,每个物品类型都有一些物品,Goemans 等在文献[11]设计了一个最优算法。这些工作激励我们研究带等级约束的多重工件调度问题(为了简便,我们把这个问题简记为HSBT 问题),其中每个客户提交一些相同的工件。在本文,对于两台平行机上的HSBT 问题,我们设计了一个在线算法和一个半在线算法。
2 预备知识
在经典的带等级约束的平行机排序问题中引入客户概念。两台平行机上的HSBT 问题描述如下:给定问题实例I=(M,N,J,a) ,其中机器集M={M1,M2}有两台机器,客户集N={1,2,…,n}有n个客户。客户i有ai个相同的工件,客户i的工 件 集Ji={Ji,1,…,Ji,ai} 。所有客户的工件集为了方便叙述,令p表示客户i的每
i一个工件的加工时间。在这里,客户被分为金卡客户和银卡客户,金卡客户的工件等级较高,银卡客户的工件等级较低。对于i=1,2,…,n,若客户i为银卡客户,则客户i的每一个工件只能在机器M1上加工;若客户i为金卡客户,则客户i的每一个工件可以在两台机器中的任意一台加工。n个客户的工件被分配给这两台机器,我们可以得到一个调度 (S1,S2),其中Sk(k=1,2)表示分配给机器Mk的工件集。t(Sk)表示机器Mk的完工时间。目标是寻找一个调度方案,使得机器的最大完工时间最小。G1表示银卡客户的工件构成的集合,G2表示金卡客户的工件构成的集合。t(Gk) (k=1,2)表示工件集Gk中所有工件的加工时间总和。
3 在线算法
当客户i到达时,更新Pi为已到达工件的最大加工时间,更新Ti为已到达工件的加工时间总和的一半,更新Di为已到达银卡客户的工件的加工时间总和。表示在调度客户i的工件后,机器Mj加工的工件集。明显地,。在这里,我们用COPT表示用最优离线算法求解实例得到的目标值 。令Li=max{Pi,Ti,Di} ,显 然COPT≥Li。在本文的在线算法中,当客户i到达时,如果客户i为银卡客户,则客户i的所有工件被分配给机器M1加工。若客户i为金卡客户,则客户i的qi个工件被分配给机器M2加工,剩下的工件被分配给机器M1加工,其中。

引理1根据在线算法,如果客户i为金卡客户且qi<ai,则 (ai-qi)pi≤Li。
证明:如果客户i只有一个工件,即ai=1。根据 引 理 条 件 ,则qi=0 ,有 (ai-qi)pi≤Li。若ai≥2,根据ai-qi的值,分两种情况讨论。
情况1:ai-qi≥2
根据在线算法、Ti和Li的定义有
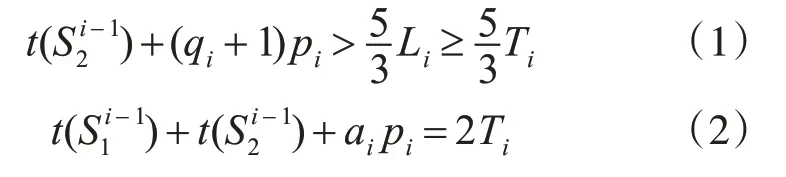
根据式(2)和式(1)有
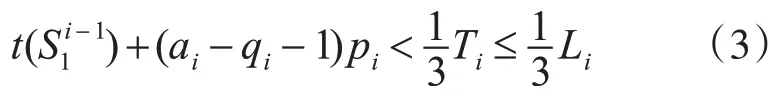
因为ai-qi≥2 ,所以ai-qi-1 ≥1,再结合式(3)有
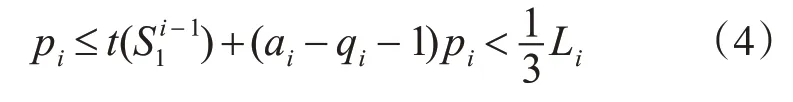
结合式(3)和式(4)有

情况2:ai-qi=1
根据此时ai≥ 2 有
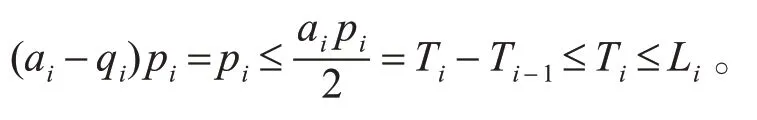
综上可知,引理1成立。
引理2根据在线算法,如果客户i为金卡客户且qi<ai,则成立。
证明:根据在线算法和引理1有
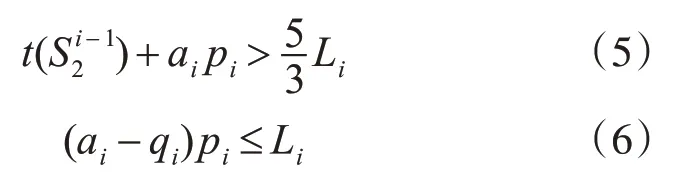
根据式(5)和式(6)有
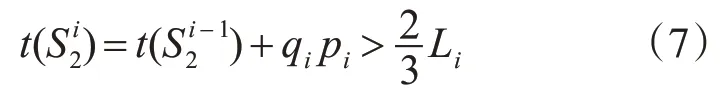
根据Li和Ti的定义有
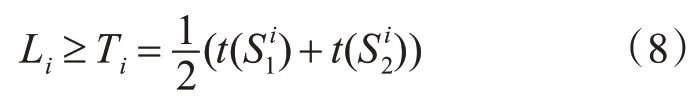
根据式(7)和式(8)有
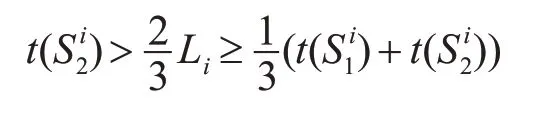
因此引理2成立。
定理3表示在线算法求解实例得到的目标值。
证明:假设定理不成立,则存在极小反例(极小反例是指最少客户个数的反例)。对于极小反例,机器的最大完工时间在加工完最后一个客户(客户n)的工件后才能被确定,因此
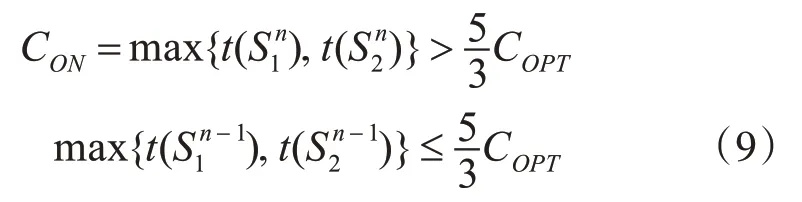
根据客户n是金卡客户还是银卡客户,分两种情况讨论:
情况1:客户n是金卡客户。
如果客户n的工件都被分配给机器M2加工,根据在线算法有
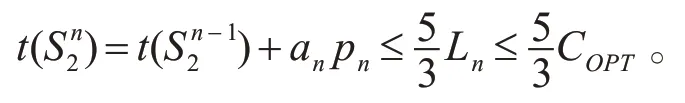
这与式(9)矛盾,因此客户n的工件至少有一个被分配给机器M1加工。因此有
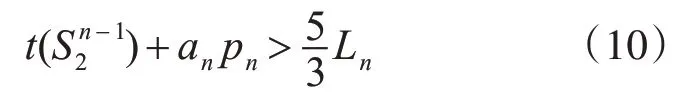
根据式(8)和式(10)有
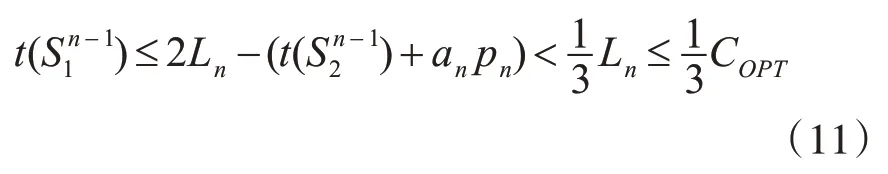
又由引理1可知 (an-qn)pn≤Ln≤COPT有
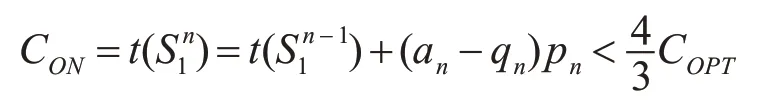
这与极小反例矛盾。
情况2:客户n是银卡客户。
根据极小反例的定义有
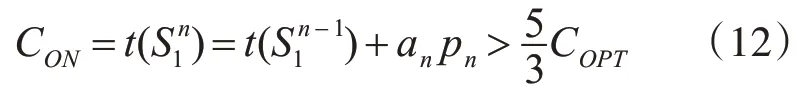

由引理2可知
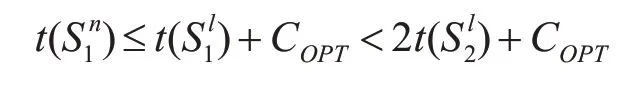
根据式(8)、式(12)和Ln≤COPT有
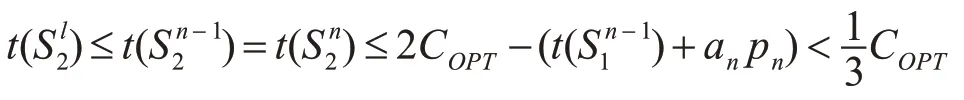
因此
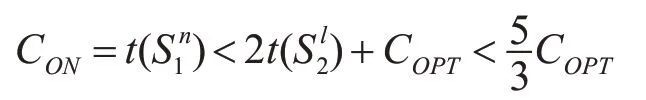
这与极小反例矛盾。因此,定理3成立。
4 半在线算法
在这一部分,我们研究在调度开始前已知所有工件的加工时间总和为的半在线排序。令显然C≥HT。在这里,OPT CSEMI表示半在线算法求解实例得到的目标值。在半在线算法中,当客户i到达时,如果客户i为银卡客户,则客户i的所有工件被分配给机器M1加工。如果客户i为金卡客户,则客户i的qi个工件被分配给机器M2加工,剩下的工件被分配给机器M1加工,其中。

引理4在半在线算法中,如果客户i为金卡客户且qi<ai,则 (ai-qi)pi≤HT。
证明:引理4的证明与引理1类似。
引理5G1至多含有一个银卡客户的工件。
证明:假设引理5 不成立。G1包含两个不同的银卡客户的工件,不妨设这两个客户为i,j。如果删除客户j而且重新定义客户i的工件大小令pi=(ai pi+aj pj)/ai,我们将得到一个客户数更少的反例。这与极小反例矛盾。
引理6。
引理7S1∩G2只含有一个金卡客户的部分工件。
证明:根据极小反例的定义有
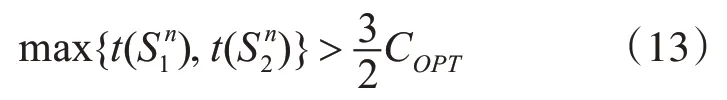
引理6 表明S1一定含有金卡客户的部分工件。假定S1包含两个不同的金卡客户的部分工件,设这两个客户分别为i,j(i<j)。
根据半在线算法和客户i的定义有。
对于客户j有 (aj-qj)pj>HT。
根据客户i,j的定义有qj)pj> 2HT。
这与HT的定义矛盾,因此引理7成立。
定理8。
证明:假设定理不成立。对于极小反例,机器的最大完工时间在加工完最后一个客户(客户n)的工件后被确定,因此
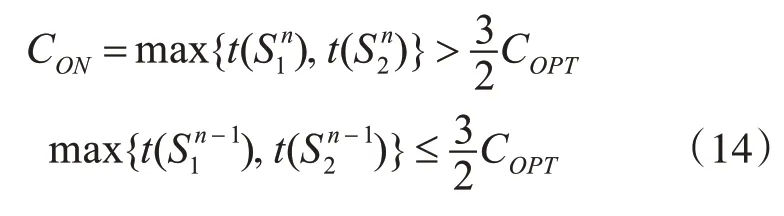
根据客户n是金卡客户还是银卡客户,分两种情况讨论。
情况1:客户n是金卡客户。
如果客户n的所有工件分配给机器M2加工,则有根据极小反例,则有又因为这与式(14)矛盾。
因此,客户n的部分工件一定被分配给机器M1加工。
这与引理4矛盾。
情况2:客户n是银卡客户。
根据极小反例有CSEMI=t(S1)。由引理5 和引理 7,有S1={Ji,qi+1,…,Ji,ai,Jn} ,其 中 {Ji,qi+1,…,Ji,ai}=S1∩G2。
然后,我们有
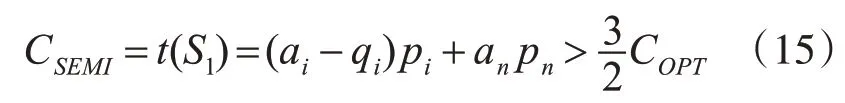
但是根据引理5 和引理6 有an pn=t(G1)<结合式(15)有 (a-q)p>C≥iiiOPT HT,这与引理4矛盾。
综上可知,定理8成立。
5 结语
对于两台平行机上的HSBT 问题,本文设计了一个竞争比为5/3 的在线算法和一个竞争比为3/2的半在线算法。接下来,当机器台数m为固定常数时,我们希望给出该问题的一个近似算法和一个FPTAS。
