基于粗糙集和动态模糊神经网络的股市预测研究*

王 峥 温光洒 邱秀连

（1.南京烽火星空通信发展有限公司 南京 210019）（2.武汉邮电科学研究院 武汉 430074）

（3.南京烽火天地通信科技有限公司 南京 210019）

1 引言

股票作为一种资本积累手段，其变化态势常被用于衡量现代市场的发展状况，它的出现和发展促使了交易市场的更新以及经济资源调配制度的完善，有利于社会发展和资源的高效利用。对整个国家的经济体系而言，资本市场扮演了一个不可或缺的角色，常被认为是国家经济实力的真实写照。

所以，如何在一定程度上通过算法预测股市的短期走向，降低投资者所要承担的风险就显得尤为重要。但是，根据分析能够明显看出股票数据存在着明显特征：1）数据是跳跃的；2）数据含有噪声；3）非线性特征明显［1］。显然，股票市场一直都是一个十分复杂的非线性系统［2］，其价格波动受到了许多外部环境的共同作用，且自身的噪声性表现也十分突出，所以针对股票价格的随机性与不确定性问题，如何判断其未来走势和通过什么方法进行预测，就成为了广大学者的研究热点。

2 股价预测方法概述

为研究股票复杂多变的特性，众多国内外各领域的学者也针对这一问题提出过大量的研究方向。Jacek 等［3］提出了一种基于数据分类方法识别的股票预测模型，Salam 等［4］使用两种聚类方法进行预测，Deng等［5］设计深度学习网络来对市场状态进行学习，Peng 等［6］设计了一种结合词嵌入和深度学习方法的股票预测模型，Li 等［7］使用结合灰色神经网络和马尔科夫方法的模型研究股票价格。而在研究过程中，因为人工神经网络拥有优秀的非线性映射能力，可以更为直观地体现股票价格波动的动态变化特性，所以基于神经网络的股票预测模型，也就成为了股市预测研究的热点［8］。在前期的分析研究中，学者多采用了静态的BP 神经网络来尝试进行股市预测［9］，但其容易陷入局部最优解的局面，无法保证预测的准确性。而在加入模糊集后，对于股价系统的预测精度得到了提升［10～11］，但在构建初始神经网络模型时对模糊规则的确定却是一个很大的难题，需要进行大量的理论实验来确定参数，其过程繁琐且效率较低。若单纯运用动态神经网络来进行预测时，没有模糊理论的支撑，又会导致其泛化能力稍显薄弱［12］。基于上述原因，本文拟采用动态模糊神经网络来进行股市预测研究。并且，为了解决模糊系统中的知识抽取问题和避免初值选择的任意性［13］，采用分级学习的方法来使算法模型变得更为高效。

另一方面，模型的输入变量的选择也在很大程度上影响了预测结果的精度，并且运用粗糙集理论进行股价预测的例子也屡见不鲜［14～15］。所以，本文在此引入粗糙集理论来对原始数据进行预处理，去除冗余信息，选择与待预测量相关性大的参数作为算法模型的输入，使得预测结果更为精确有效。

3 算法模型综述

3.1 粗糙集理论（RS）

粗糙集作为一种处理不确定性问题的数学工具，它对于人工智能和认知科学都非常重要，并且为粒度计算、近似推理、决策分析、知识获取、数据挖掘和支持系统、模式识别、专家系统、控制科学等领域的信息处理提供了行之有效的理论框架。所以，对于粗糙集理论的研究一直都收到了广泛的关注，而且模糊集合创始人曾高度评价这一理论，提出把它作为现代软计算基础理论之一［16］。

本文希望加入粗糙集理论，通过信息熵的计算得出更为合理的输入参数。算法中用U 来代表论域，用C 来表示属性集合中的条件属性集合，把D作为决策属性集合。算式中U 上基于条件属性集合C 及决策属性集合D 的等价关系分别表示为RC和Rd。而所谓的信息熵其实就是粗糙集理论中对知识不确定性进行度量的一种指标。其相关概念如下。

定义1：Rc在U上的子集的概率分布为

式中：[X]∈U/Rc表示U的等价类；|[X]|是集合[X]的“势”，在此可以表示为[X]所含元素的个数。

定义2：令

称H(Rc)为知识Rc的信息熵。

定义3：令

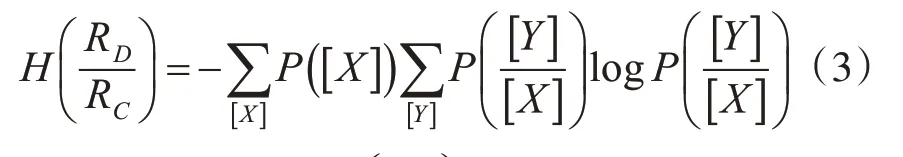
定义4：令

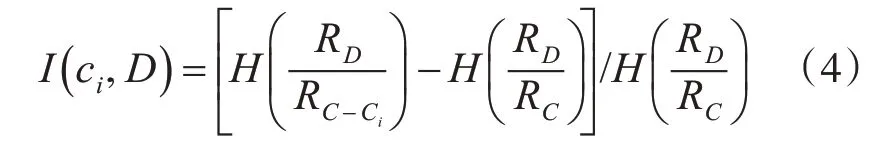
在此用I(ci，D)表示属性ci相对决策属性D的重要程度，该值越大说明在条件属性C中属性ci对决策属性D越重要、二者的相关程度越大。若该值过小，则说明属性ci是多余的，可从条件属性集合中去掉，属性集C简化为C-{ci} 。

3.2 动态模糊神经网络（DFNN）

常用的模糊系统其主要不足在于大部分的算法模型都是针对于静态问题进行设计的，使得其算法的模型适用范围太过于局限，对于动态问题的研究显得十分乏力。而在实际生活中，实验研究对象大多存在动态特性，其动态变化多与时间相关，这就使得探讨动态特性的算法模型具备更为实际的意义。而且，动态模糊神经网络（DFNN）的各个参数具有其实际的物理意义，可以根据计算得出的输入参数及对应历史数据对构成的DFNN 网络进行有监督学习，完成对于模糊系统的参数辨识任务。所以，本文拟用区别于模糊神经网络的动态模糊神经网络来实现对股票系统的预测研究。

3.2.1 算法模型结构

DFNN 共分为五层，分别为输入层、隶属函数层、T-范数层、归一化层和输出层，如图1所示。

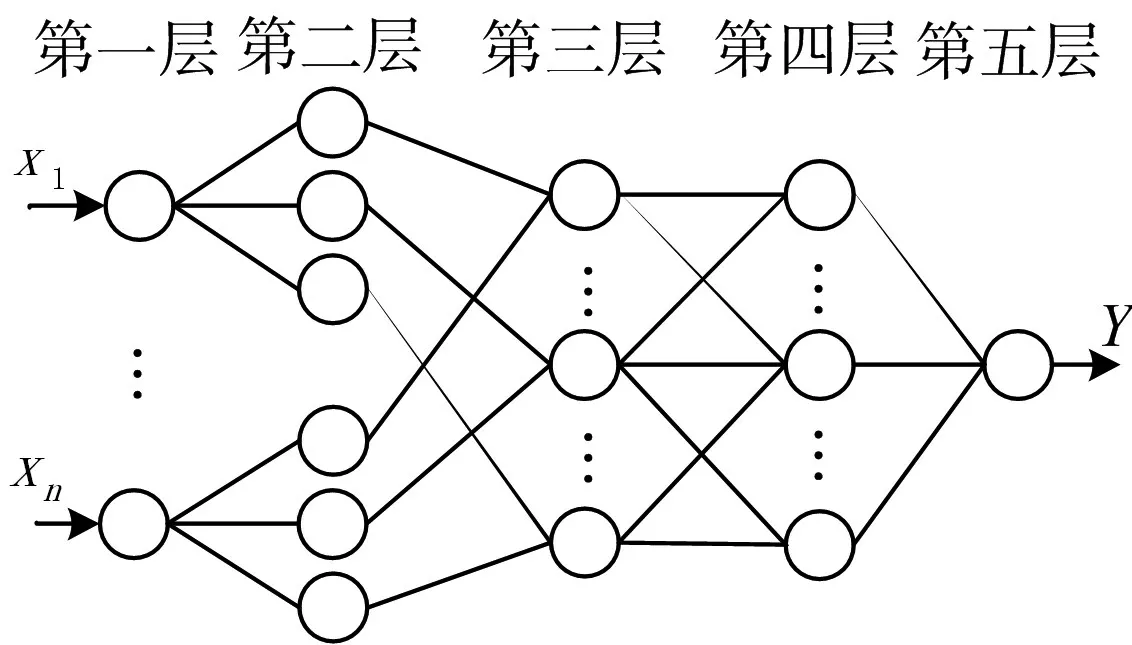
图1 D-FNN网络结构

第1 层：称为输入层，每一个节点直接与输入向量xi相连，用于接收样本的输入参数。

第2 层：称为隶属函数层，其中每一个节点单独表示一个隶属函数，相关节点的隶属函数可以通过下述高斯函数来进行表示：

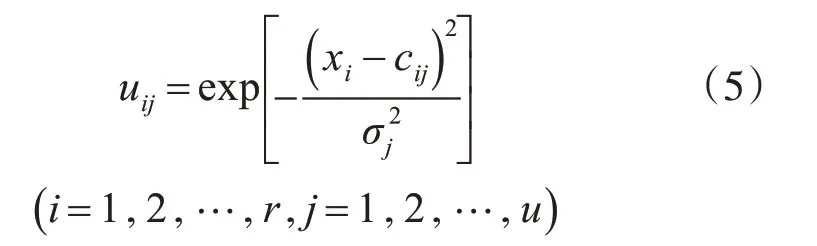
上式中，uij是xj的第j 个隶属函数，cij是xi的第j个高斯隶属函数的中心，σj是xi的第j个高斯隶属函数的宽度，r是输入变量数，u是隶属函数的数量，也代表系统总的规则数。

第3 层：称为T-范数层，每一个节点分别代表一个可能的模糊规则中的IF-部分。因此，该层节点数反映了模糊规则数。第j个规则Rj的输出为

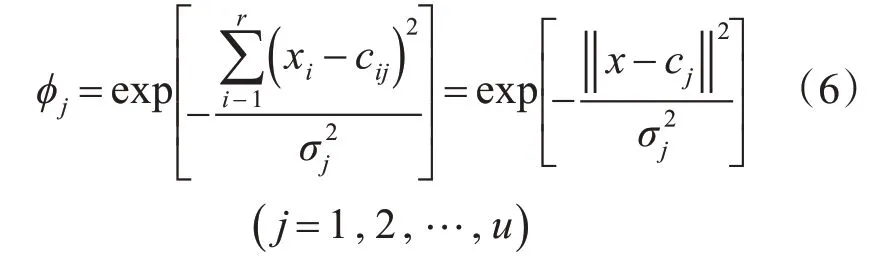
第4 层：称为归一化层，称这些节点为N 节点。其中，N 节点个数和系统模糊规则的节点数一致。该层中，第j个节点Nj的输出为

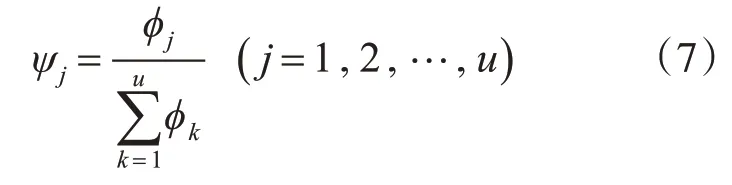
第5 层：称为输出层，该层中每一个节点分别表示一个输出变量，其值为所有输出信号的叠加：

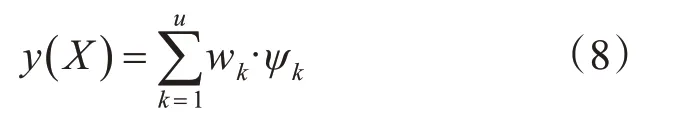
其中，y 表示算法的输出，wk则为THEN-部分（结果参数）或者第k个规则的连接权。

3.2.2 模型的学习算法

本文采用的动态模糊神经网络相较于传统模糊神经网络最大的特点就是算法模型的模糊规则数不需要预先进行设定。它会依据输入参数的变化自身进行更新和调整，并根据特有的规则进行判断算法是否有必要更新自身的规则或者是剪除旧有的规则。所以，其结构的确定也就是其模糊规则的确定过程。而在模型的学习算法上，本文采用如下的算法结构：根据可容纳边界、系统误差这两个参数来判别是否需要在模型中添加新的模糊规则，使用分级学习、最小二乘法（LLS）来计算算法模型中其余参数的权值系数，最后在模糊规则的修剪中拟用误差下降率法（ERR）。

1）分级学习

分级学习的主要思想是指算法模型中每个RBF 单元的可容纳边界并不是固定不变的而是通过下列步骤来进行动态调节的。

起初，可以设置较大的可容纳边界，来实现算法的全局学习。然后，随着不断学习的过程，逐渐缩小边界，开始所谓的局部学习。根据这个思想，不断地缩小每个RBF单元的有效半径和误差指数。

而这也就使得算法模型中的系统误差ke和可容纳边界kd的大小不再是一个预先设定的常数，而是根据学习速率的下降来慢慢降低的。二者的计算可以用下列式子来表示：

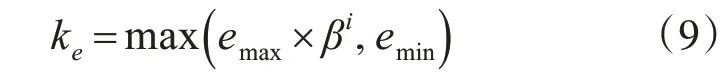
式中，emax为预先定义好的最大误差；emin为期望的D-FNN精度；β(0 ＜β＜1) 为收敛常数。

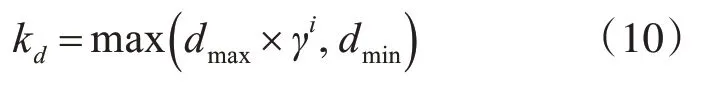
式中，dmax为输入空间的最大长度；dmin为所关心的最小长度；γ(0 ＜γ＜ 1) 为衰减常数。

分级学习的一个重要步骤就是需要先找出算法模型中输出误差较高却未被已确立的模糊规则所覆盖到的地方，这个过程也被定义为粗学习。而当ke，kd分别达到预定的emin和dmax时，这个阶段的学习就被定义为细学习。

2）模糊规则的剪除

本文拟用误差下降率方法（Error Reduction Rate，ERR）作为规则的修剪策略，其算法核心在于分别计算出各个规则关于模型输出的误差下降率，然后分析现有规则对于算法模型的贡献值，并通过预先设定的阈值来删除那些贡献值小的规则节点，该方法具有明显的物理意义和稳定的数字计算。

上式中，D=TT∈Rn被称为系统的期望输出，叫做回归向量，θ=WT∈Rn包含实数参数，式中的误差向量E 被包含于Rn的范围中，且回归量hi和其不相关。

若H的列数小于其行数，可以进行分解得到：

通过上式易得：

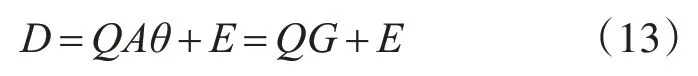
G的线性最小二乘解为

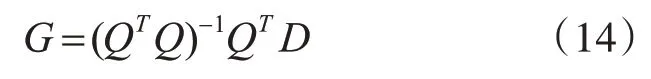
也可以写成下式：

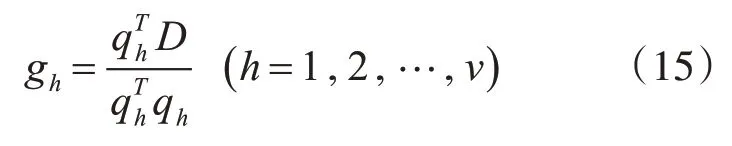
G和 θ 满足：

当h≠j时，因为qh和qj正交，D 的平方和或者输出能量可以表示为

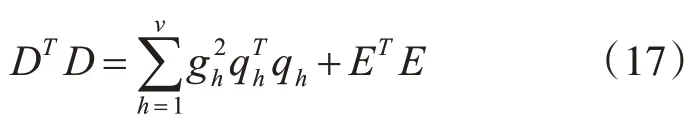
去掉均值后，D的方差为

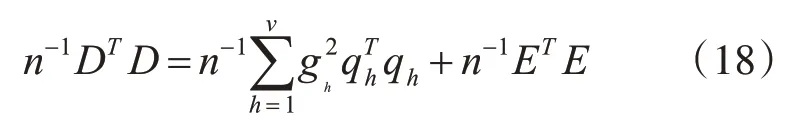
其中，回归量qh对系统的期望输出方差中的一部分是由造成的。误差err的定义：

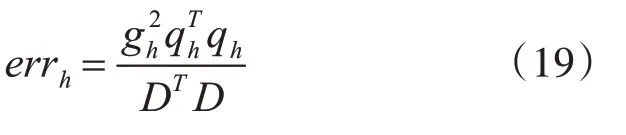
带入上式易得：

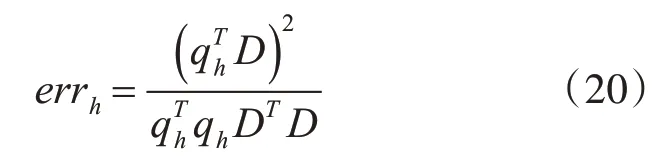
而这一算法的目的在于计算第i条模糊规则的重要性：

其中δS就是与第i个规则相关的（r+1）个err。

在算法中通过ηi的值来代表模糊规则对于系统的必要程度，当ηi值较大，则表示这个模糊规则在系统中比较重要，不能剪除，但是若：

式中，kerr为人为设定的阈值。表明该规则在系统中已不再是必要的，可以进行剪除。

4 算例分析

本文使用苏宁易购（002024）、招商银行（600036）、华夏幸福（600340）的真实交易数据作为数据集，包含开盘价、收盘价等基本信息及WR、RSI 等多种技术指标。考虑到股票技术指标分为超买超卖指标、趋势指标、能量指标、量价指标、大盘指标、分时指标、强弱指标等多种，在实际应用中，投资者主要是参考分析前四类指标，即超买超卖指标、趋势指标、能量指标和量价指标［17］。根据股票属性及相关文献研究成果，从四个指标类型中选部分指标及基本信息进行初步筛选后确定16 个分析指标，然后对输入数据进行离散化处理，再根据粗糙集理论的属性约简算法进行输入参数的筛选。

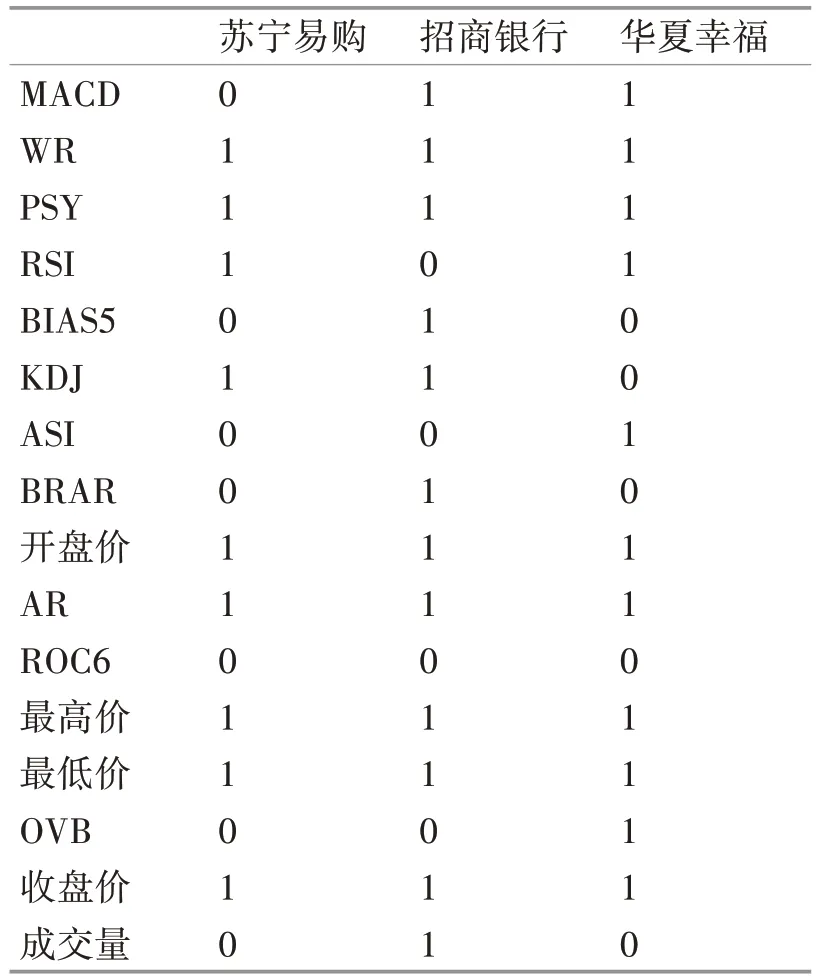
表1 约简结果

由表1 可以看出WR（威廉指数）、PSY（心理线指标）、AR（人气指标）、开盘价、最低价、最高价以及当日收盘价等7 个属性在三次约简实验中都有保留，可见这些指标在预测分析股票的价格变化时具有重要作用，故选定为输入属性。

本文研究的预测算法数据集以苏宁易购的交易数据为代表，选择 2016 年 11 月到 2018 年 5 月的共381 组记录。对原始数据进行归一化处理后，取前330条数据作为训练数据，后51条作为测试数据进行算法模型的训练预测。

在运用本文方法进行训练预测的同时，通过构建合适的BP 神经网络及模糊神经网络系统（FNN）模型进行训练预测，对预测结果进行对比验证。

由图2明显可以看出DFNN方法的预测结果更为贴合实际输出曲线。相对而言，图中BP 神经网络与FNN 方法的预测曲线虽然大致走向与实际输出曲线一致，但都存在了多个点的预测数据严重偏离实际输出的现象。其次，对实验的结果数据进行分析，为了衡量预测结果与真实结果之间的误差，本文使用了均方误差MSE、均方根误差RMSE 与平均绝对误差MAE 作为算法评价标准，并对多种算法模型运行时RMSE值的变化进行对比分析。

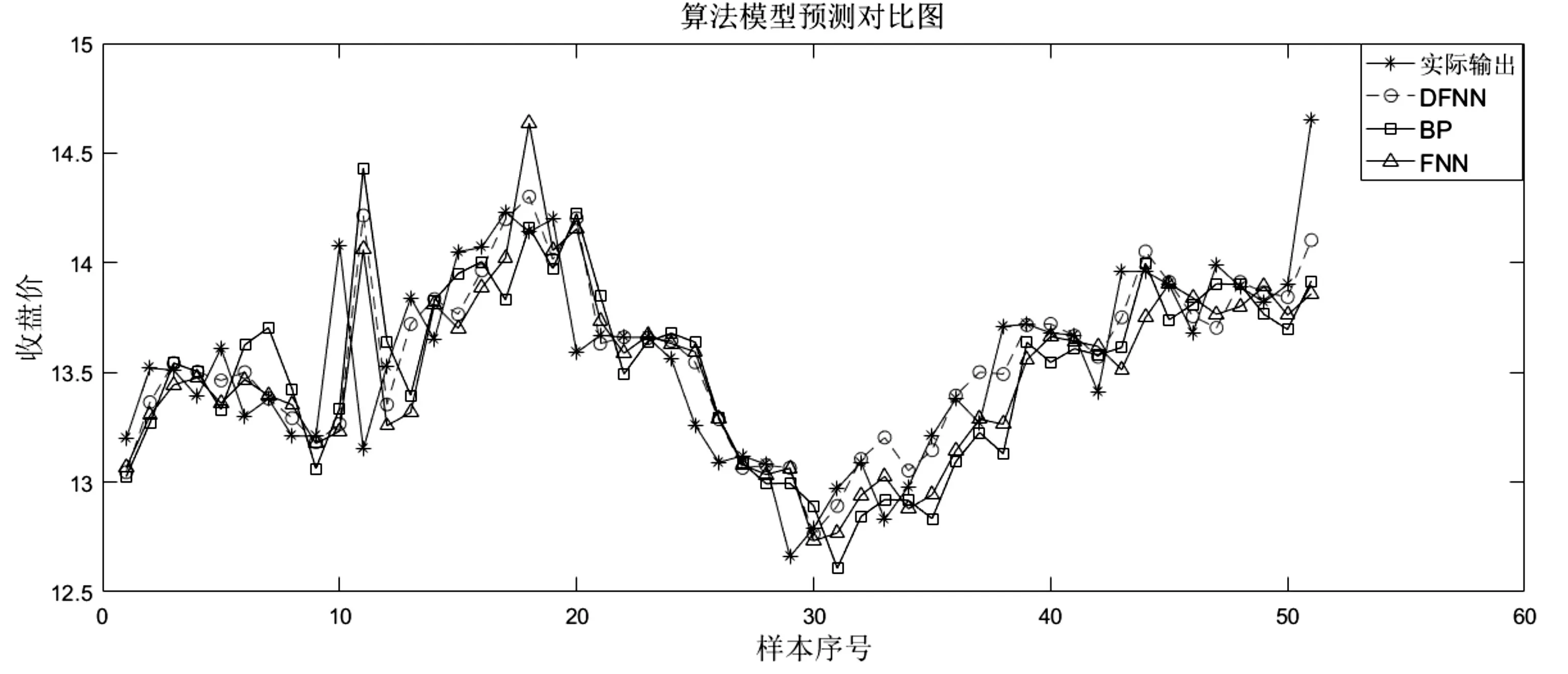
图2 多种算法模型预测结果对比

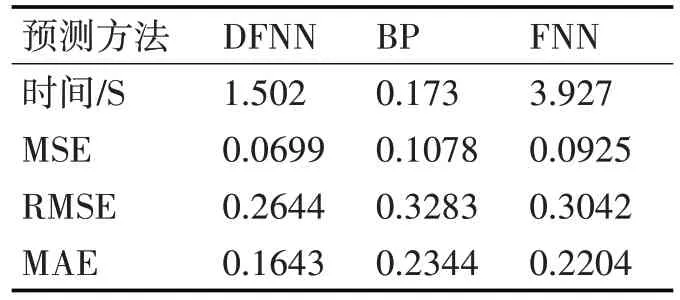
表2 算法结果对比

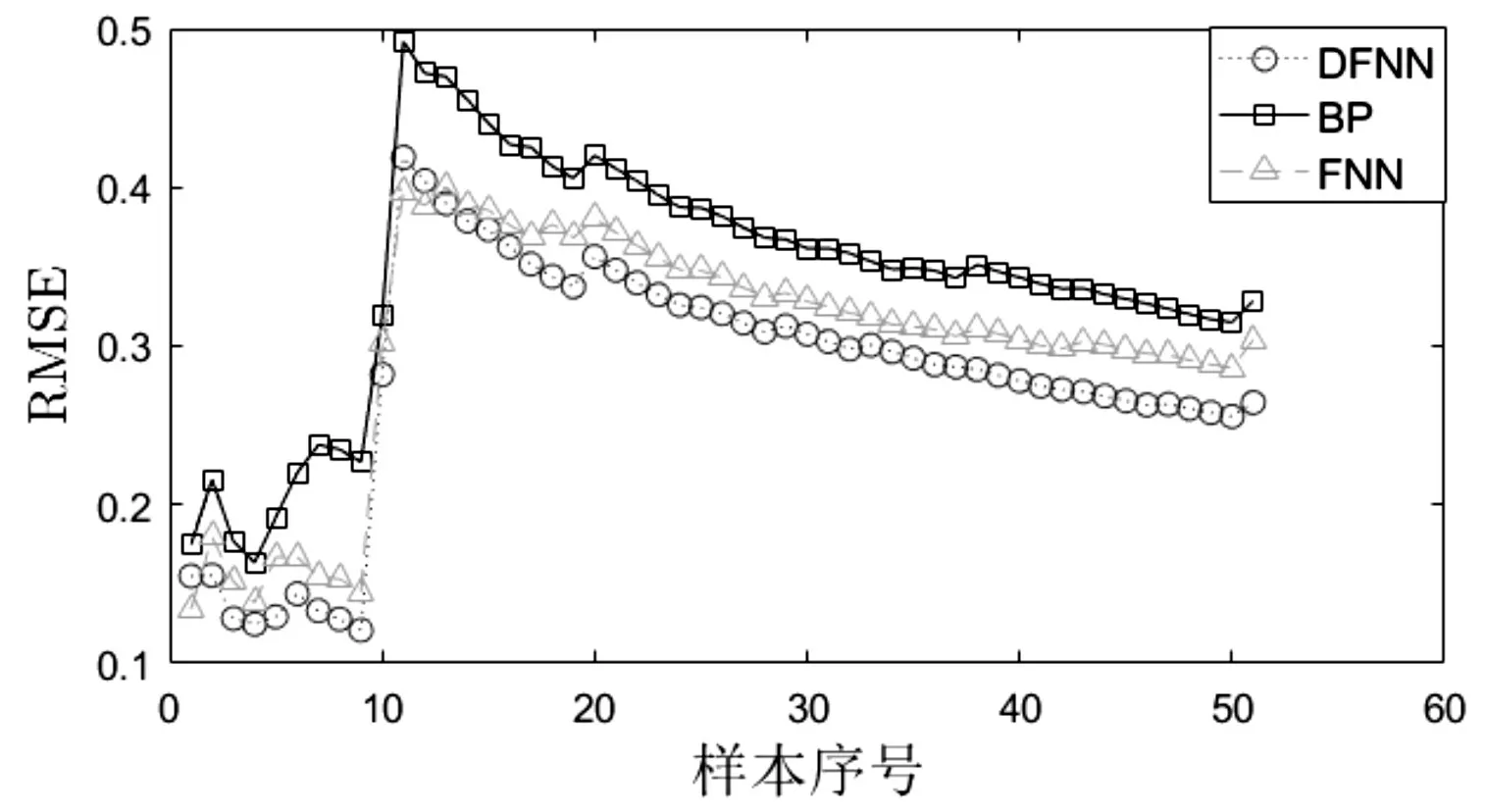
图3 算法模型RMSE变化图

由表2 与图3 可见，本文方法的预测精度与收敛速度明显高于FNN模型，而BP算法虽然高效，但其易陷入局部最优解，结果精度差。分析结果，从算法思想上来看，BP 算法根据各节点权值间的关系简单地计算得出输入数据与预测结果间的联系。传统的FNN 算法在模型构建的过程中，关于模糊规则和隶属函数方面都太过于依赖专家的主观意见。而本文方法在预处理阶段通过信息熵算法去除了大量的冗余信息，给出了更为合理的输入参数，而且是根据对历史数据的训练学习来计算得出更契合实际的系统参数，切实地体现了输入参数与预测结果间的映射关系，在结果预测上相较于另外两种算法都显得更为精确合理。

最后，通过实验可以表明：1）通过粗糙集理论来筛选和待预测量关联度高的属性作为算法输入，确保了输入数据的合理性，切实地提高了系统计算的运算效率，同时也提高了算法的预测精度。2）区别于传统动态模糊神经网络，采用分级学习的思想改变算法结构，有效地提高了算法的运行效率，使预测结果更为准确。3）与传统算法模型不同，动态模糊神经网络具有动态映射机制，可以很好地处理动态问题，并且其自身存在的自我调节能力避免了BP 神经网络模型易陷入局部最优解的缺陷。4）运用动态模糊神经网络算法模型进行预测时，存在模糊规则的剪除过程，相较于模糊神经网络而言，后期实验结果更加的准确和高效。

5 结语

本文针对股票价格预测问题，提出了一种基于粗糙集和动态模糊神经网络的股票预测模型。利用RS 出色的属性约简能力，在很大程度上消除了算法模型输入数据的冗余信息，而DFNN 适用于对非线性系统进行预测分析，将二者有机的结合，优化了网络拓扑结构，降低了运算的复杂度，并且在模型学习算法中采用分级学习的思想，使得实验结果更加的高效和准确。最后通过分析测试集数据得到实验结果，证明了本文方法的有效性。