基于低年级基数与序数教学的思考

茅新苗

摘  要：“基数”与“序数”的理解，贯穿于解决问题之中。通过问题的解决，逐步理解和感悟。学生通过自己身边的观察，参与身边的活动，在亲身体验中，才能进一步去理解“基数”“序数”，并加以运用。

关键词：基数与序数;低年级;形象思维;错误分析

在教学基数与序数时，学生往往对概念产生混淆，分不清哪里该用基数，哪里该用序数，而基数”与“序数”又是两个相对比较抽象的概念。学生对这两个概念的不理解，导致题目出错。通过怎样的手段，使一年级的学生充分感知、理解这两个概念，并正确解答这类题呢？引发了笔者对低年级“基数”“序数”教学的思考。

一、让老师们尴尬的基数与序数教学

前几天，低年级的几位数学老师在办公室里诉苦说：“现在涉及到基数与序数的内容，真是让人头痛。”我插话问：“那是什么题？你们是怎么教学的呢？”王老师：考虑到学生对“之间”不理解，我特意用“画图法”来教学。教的时候，学生挺理解的，但真的让学生自己做了，各种错误都来了。张老师：我认为数数法或画图法太麻烦了，如果数字一大，再用这种方法，不是费时吗？我主要教学生用列式计算的方法来解决。如15-10-1=4（人）。可是，我感觉自己已经讲得很清楚了，但学生好像还不懂，看来我还得再花一节课的时间来巩固这块内容。

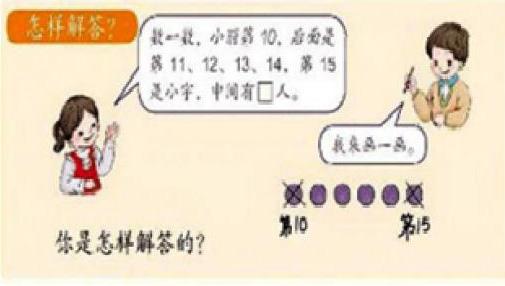
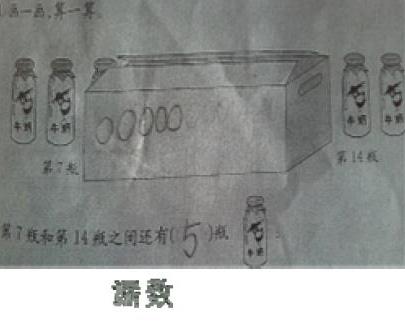
两位老师对教材有自已的理解和把握，我们再回过头来看看教材内容（如图）。

这部分的内容是第六单元“11～20各数的认识”最后一个例题，主要是让学生综合运用所学的知识，来解决问题。同时也是为了让学生进一步深化对数的大小、基数、序数的理解。王老师在教学时，只注重用“画图法”解决问题，显然削弱了对数的大小、顺序的理解。张老师在教学时，不仅违背了编者意图，而且也违反了低年级学生形象思维的特点，把孩子容易理解和掌握的方法置之一旁。而列式解答，要正确理解“15—10—1”这个算式的含义有一定的难度。

二、让学生们头痛的“基数”“序数”

【错例一】 数数困难

从学生的错误中，发现部分学生在数数时存在漏数或重复数的现象，不能一一对应地数，数数还不过关。

【反思】以学生的认知为基点，处理教学内容。

教师要创设多种情境活动，帮助学生理解。如利用小棒摆一摆，数一数。其次利用直尺可以进行数的多种知识的教学。读数、写数、数的前后顺序，数的大小比较，数的排列等。对一年级的学生，只有牢固掌握11～20各数，才能正确解决问题。

【错例二】曲解题意

“几和几之间”与“从几到几”是两个不同的概念，同样是运用画图法来解题，但学生把他理解成一个意思导致错误。

【反思】对比呈现问题，提高读题能力。

一年级学生不能很好地理解题意，教师可以通过读题、比较，帮助学生理解题目的意思。如前面提到的：在小猴与小鹿之间有（）只小动物;从第10页读到第18页共读（）页。这两个问题的意思是完全不一样的。“之间”是除去头尾中间部分的意思，学生容易理解。但对于“从几到几”是算上头尾所有的部分，这学生理解起来有一定的困难。其实这两个问题，也是今后学生学习“植树问题”的雏形，两头都不种和两头都种。在此，更加要重视对这类题的教学。如何让学生自己去感悟和理解呢？

【错例三】方法选择不当

学生根据自己的学习能力，应灵活选择解题方法，往往因为各种原因，不能灵活运用，导致解题错误。

【反思】解题方法的多样化，学会择优选择。

在众多的解题方法中，学会选择适合自己的方法，能解决问题的方法才是好方法。像张老师，硬要学生用列式的方法来解决问题，导致学生不理解，到底是两数直接减，还是两数减后加1，还是两数减后再减1，出现解题时乱用的现象。

三、基数与序数教学的对策探讨

《数学课程标准》中明确提出，要让学生在实践活动中去解决日常生活中和其他学科学习中的问题，增强应用数学的意识。学生通过自己身边的观察，参与身边的活动，才能进一步去理解“基数”“序数”，并加以运用。

1.充分挖掘生活资源，丰富体验，帮助理解

低年级学生喜欢做游戏，如“老鹰捉小鸡”的游戏。在玩之前，让学生说一说，“鸡妈妈”带着几只“小鸡”做游戏，分别说说，第一只，第二只……各是哪只小鸡？到游戏结束时，再讓学生说说，老鹰一共捉了几只小鸡？第一只被“老鹰”捉到的是哪只小鸡？让被捉到的几只小鸡一起表演一个节目，或让第几个被捉到的小鸡表演一个节目。这些都有助于学生对基数与序数的理解。

2.努力培养读题能力，分析整理，正确解答

一年级学生由于识字量少，看图、读题能力，对信息的搜集、分析等能力较弱。平时结合具体的题目，注重培养学生这方面的能力。如同样是学生排队。①排队做操，小红的前面有8人，她的后面有6人，这一排一共有多少人？②排队时，从前往后数，小红排第8，从后往前数，她排第6，那她们这一排一共有几人？学生有的列成8+6=14（人）;有的列成①8+6-1=13（人），②8+6+1=13（人）。题目中，前面8人，是不包括小红自己的，若从前面，小红应该排在第9了。排在第8，已经包括她自己。通过这样的对比题，让学生了解读题的重要性，仔细分析，才能正确解答。

3.逐步养成检查习惯，反思提升，拓展思路

元认知理论认为：“反思是学生对自己认知过程、认知结果的监控和体会;数学的理解要靠学生自己的领悟才能获得，而领悟又靠对思维过程的不断反思才能达到。”一年级的孩子，不知道怎么去检查、反思。通俗地说，就是做完后，再想一想，还有没有不同的解题方法;对今天学习的内容还有哪里不懂。如刚才的习题：“排队时，从前往后数，小红排第8，从后往前数，她排第6，那她们这一排一共有几人？”若学生能列出不同的算式：①8+6-1;②8+5;③7+6;④7+5+1，并且能正确说明每个算式的意思，孩子的思维相当灵活，有了一个质的提升。

“基数”与“序数”的理解，贯穿于解决问题之中，通过问题的解决，逐步理解和感悟。新课程标准要求学生面对实际问题时，能主动尝试从数学的角度运用所学知识解决问题，体验解决问题问题的策略。因此教师要抓住学生的特征，努力优化我们的课堂教学，促进学生能力的发展和思维的提高。