《几何概型》教学设计
2020-06-08刘英杰
刘英杰

摘 要几何概型这节内容,前面有古典概型做基础,后面延续了概率的应用,在概率知识部分,起到了承上启下的作用。在旧知识基础上,通过类比、归纳与合情推理过渡到几何概型应该是水到渠成的,但也应该注意几何概型和古典概型的区别,如何正确建立几何概型、正确定位几何测度是本节教学的关键。
关键词几何概型;古典概型
中图分类号:G632 文献标识码:A 文章编号:1002-7661(2020)08-0198-01
在一次随机实验中,所有可能出现的结果共有限个,也就是说基本事件的个数是有限个,并且每个基本事件的出现的可能性相同,解决这样的概率问题,可以借助古典概型的计算公式来完美解决。但是对于某些随机事件,所有可能出现的结果有无限多个。比如,将一根3米长的绳子随机剪断为两截,其中一截大于2米的概率是多少?对于这样的问题,显然不再是古典概型的问题,可以借助新的概率模型——几何概型来解决。
一、创设情境—引入新课
通过一个抽奖游戏回顾古典概型的相关内容。
在长为5米的绳子上等距的挂有6个气球,其中两个气球中设有奖品,现让某位同学随机去扎破一个气球,问该同学获奖的概率是多大?
然后改变条件得到新的问题。
若绳子的长度不变仍为5米,某同学随机将一个气球挂到绳子上的某点,事件A:该点到绳子左端点的距离小于2米,则事件A的概率是多大?
设计目的目的:通过类比引出几何概型。
本环节关键:
1、通过与学生的互动,自然引出几何概型的特点和计算公式。2、分层出现定义的和计算公式,先介绍用长度比表示几何概型的概率。3、强调几何概型只和测度比有关,而和区域位置无关。
二、应用举例,完善知识体系
应用1:某人午觉醒来,发现表停了,他打开收音机,想听电台整点报时,求他等待的时间不多于10分钟的概率。
目的:学生参与,通过讨论交流得到不同的解决方案,老师点拨进一步挖掘几何概型的特征。完善定义和计算公式(用面积和体积比表示事件发生的概率)
应用2:在某档电视综艺节目中,有一个现场互动的环节,由主持人邀请一名观众从两个小游戏中任选一个去玩儿,若观众在游戏中获胜,便可领取一份精美的纪念品。
游戏需要借助一个矩形来完成,具体游戏规则如下:
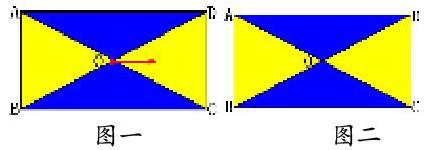
游戏一:观众随机向长方形区域内扔一粒豆子(图1),若豆子击中蓝(深)色区域,则观众获胜。
游戏二:观众随机拨动长方形中心的红色指针,若指针停止转动时停在在蓝(深)色区域(图2),则观众获胜。
如果你是参与互动环节的一名观众,你会选择哪个游戏去玩儿?说明你的理由。
目的:1、通过对比让学生体会解决几何概型问题,明确基本事件和正确选择测度的重要性。2、利用数学知识做出理智的选择,由于两个游戏的背景很相似,但研究方法又不相同,细致的同学更容易在审题的第一时间发现两者的区别,另一些同学更容易总结出解决问题的规律。肯定不同学生自身长处的同时,引导学生弥补自己的不足也是本環节的重要任务。
三、关注民生,能力提升
某公交站点,只有1路和2路公交车停靠,1路车每天早晨6:10第一趟车到达本站,以后每隔15分钟,有一趟车停靠;2路车每天早晨6:15第一趟车到达本站,以后每隔15分钟,有一趟车停靠。市民张先生每天上班乘坐1路或2路车都可以到达工作单位,张先生每天6:00~7:00之间随机到该站候车,来车就上。张先生经过20天的连续记录发现,他有13次乘上1路车,只有7次乘上2路车,张先生认为1路和2路公交车每两趟车之间的时间间隔相同,且在6:00~7:00间都有4趟车经过,所以他乘上1路和2路车的机会应该大致相等,于是张先生怀疑2路车有经常晚点和少发车次的情况发生,准备向公交公司投诉此事,你是否支持张先生的观点?
目的:1、通过实例引起学生的兴趣,并在解决问题的过程中引导学生把抽象的时间转化为具有具体几何特征的线段然后采用几何概型的知识来解决问题。让学生体会数学来源于生活并服务于生活。2、培养学生的抽象概括能力,数学建模能力。(注意:既可以转化成线段模式也可以转化成圆周模式。)3、在思辨中,让学生学会用数学的眼光去观察世界,用数学的思维去认知世界,从而提升认知能力。
四、小结
1、几何概型的概念、特点、计算公式;几何概型与古典概型的对比,用几何概型求概率的步骤等。2、概率知识在生活中应用及意义。3、通过生活中的实例让学生感受到数学在实际应用中的重要性和广泛性,从而无痕地唤醒学生学习兴趣,并根据自身特点,合理规划自己的学习。
基金项目:本文系2018度河北省“三三三人才”人才资助项目课题《生涯规划在数学课堂中的渗透》成果,项目编号:A201803084。
