基于MATLAB信号降噪方法对比研究

何会新,姚 欢

(1.中交第四公路工程局有限公司,北京100022；2.武汉理工大学道路桥梁与结构工程湖北省重点实验室,武汉430070)

在信息飞速发达的时代,我们会接触到大量的信号(声音信号、图像信号、结构振动信号等等),一般接受到的信号中或多或少的都会包含着噪声,如结构振动信号中经常由于环境、地质条件或者监测传输设备受到干扰等产生的噪声。少量噪声会影响到有用信号的识别,而大量噪声信号甚至会掩埋掉有用信息。信号的处理不光依靠高效的采集、传输和存储技术,还需要有效的降低噪声和准确提取出有用信息,降噪效果的好坏将极大的影响到后续工作的质量。因此准确的去噪将是结构健康监测、损伤识别的重要前提。已经有大量的学者对降噪方法做了相关的研究。

1992年,Donoho和Johnstone[1]最早提出了小波阈值萎缩方法,给出了阈值的选择。后来关于小波降噪阈值的选择出现了很多新的方法。刘立君等[2]将db小波改进阈值后对模具修复锤击力信号进行降噪,取得较好的效果。余腾[2]等将小波阈值改进后与EMD结合提取了润扬大桥的振动信息。尤波等[3]针对硬阈值不连续、软阈值偏差大的缺点,提出一种新的改进阈值的方法,很好的解决了两者的局限性,并且与双边滤波器结合,对图像信号进一步降噪达到更佳的结果。王旭[4]等重新构建均方根误差与平滑度变化量,从熵权法出发将两指标组合,得到新的评价指标,该指标可以准确指导小波分解以及确定分解层数。周建[5]提出一种新的改进小波阈值的算法,从仿真信号以及试验轴承振动信号来进行去噪。结果表明改进阈值之后效果更优秀。Huang等[6]提出经验模态分解这种信号处理方法,它不需像小波变换那样根据信号的先验知识来选择小波基,只需要依赖信号本身,分解快捷,真实可靠。Wu[7]提出了总体平均经验模态分解(Ensemble Empirical Mode Decompomposition,EEMD),通过在EMD的基础上叠加白噪声,再利用多次平均,降噪效果得到更一步的提升。

1 小波变换

1.1 小波变换基本原理

小波变换是基于傅里叶变换、泛函数、数值分析的发展产物。傅里叶变换可以把任一信号分解为一系列的谐波的叠加,小波变换则是把信号分解成为一系列的小波,其中小波可以被看作成平均幅值为0,时间有限并且频率幅值突变的一种函数。小波变换可以解决Fourier分析不能反映时域上局部特性的问题,Fourier变换不能得到具体时间所对应的频率,只能够得到一段时间内的频率分布。这样就使得傅里叶变换降噪效果很差,有很大的误差性。根据海森堡测不准定理,我们无法同时获得较高的频率分辨率,因此小波变换采用了多分辨率分析,它在信号高频部分采用较高的时间分辨率,在低频部分采用较高的频率分辨率,从而能对信号在时频域进行较好的分析。公式(1)、(2)分别为小波连续变换和傅里叶变换的公式

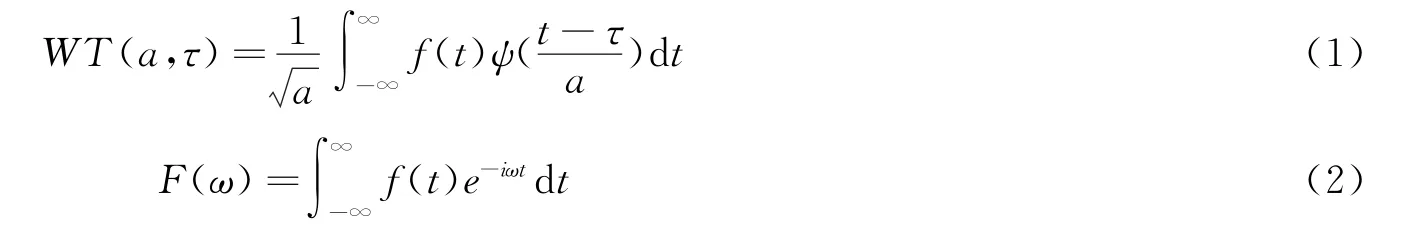
式中,a为尺度因子,影响着小波函数的伸缩；τ为平移量,控制小波函数的平移；其中尺度因子和平移量分别对应着频率和时间。小波分解是指在不同尺度做正交小波变换来得到尺度系数和小波系数,通过设置阈值来筛选小波系数,以此来去掉高频的噪声,只保留有用的信息。

1.2 小波阈值准则的选择

小波降噪的关键则是阈值法的选取,其中最常用的两种则是硬阈值法和软阈值法,硬阈值法规定当信号小波系数的绝对值大于阈值时则不变,否则为0,如式(3)所示。软阈值准则规定当信号的小波系数绝对值大于阈值的时候令信号值逐渐向0逼近,如式(4)所示。

式中,T 为阈值；y 为阈值化后的小波系数；x 为原小波系数。关于阈值T 的具体取值则主要根据4种阈值法则来取值:Minmaxi准则、Sqtwolog准则、Heursure阈值准则、Rigrsure准则。

1.3 分解层数的选择

分解层数没有一个固定的选值,应根据不同信号或者不同信噪比的同一信号具体调节。当分解层数过大的时候,会有更多的小波空间系数,当阈值对更多的小波空间系数处理时可能会丢失掉更多的有用信息成分,反倒使得信噪比下降。分解层数过少又将存在消噪不充分,使得信号中还将继续残留着大量的噪声。

1.4 小波基的选择

小波基的选择要按照正交性、对称性、正则性、紧支性以及消失矩这4个原则来选取,更要根据信号本身的特性来选取,不同的信号可能适用不同的小波基,小波基具体的选择规则还没有一个明确的规定,需要结合信号本身,需有一定先验知识,不同小波基选取可能会导致不同的结果,这也是目前小波分解降噪存在的一个弊端。当信号连续性和光滑性较好的时候,宜采用Sym8小波,主要是因为Sym8小波基有着良好的光滑性以及连续性。而当信号的连续性较弱的时候,则应该选用Haar小波基。而对于类似结构振动、微震信号这类非稳态信号则更适用于db小波基。总的小波分解流程可以概括为:1)选择小波基,确定分解层数,确定阈值准则；2)含噪信号小波分解；3)保留最大尺度下的低通滤波分量,对其他尺度分量进行降噪处理。

2 经验模态分解

经验模态分解简称EMD 法,是由HUANG N E 等人于1998年提出的一种新型自适应信号时频处理方法,适用于非线性非平稳信号的分析处理。

该方法依据数据自身的时间尺度特征来进行信号分解,无须预先设定任何基函数。这一点与建立在先验性小波基函数上的小波分解方法具有本质性的差别。因此EMD 方法适合于分析非线性、非平稳信号序列,具有很高的信噪比。EMD 方法是通过数据的特征时间尺度来获得本征模函数,然后分解数据的数据分解法。最终可以得到振荡模式为一零均值的、可以通过希尔伯特变换有效地求得其各时间点上瞬时频率的信号。在海洋、大气、天体观测资料与地震记录分析、机械故障诊断、密频动力系统的阻尼识别以及大型土木工程结构的模态参数识别方面都得到广泛的应用。EMD 分解流程:1)找出原数据序列极大值点；2)通过三次样条插值函数拟合得到原数据上包络线,找出极小值点。3)再通过三次样条插值函数拟合得到原数据下包络线。4)原数据序列减去平均包络,得到新序列。

3 评价指标

为了定量对比降噪的好坏,该文从信噪比和均方差以及和原信号的能量百分比来评价。信噪比(signalnoise ratio,SNR)指的是有用信号的输出功率与噪声的输出功率之间的比值。信噪比越大则表明有用信号所占比例越大,越接近最纯的信号,干扰越小。信噪比越高越好,因此可以用降噪前的信噪比与降噪后的信噪比对比,信噪比提升的越多则可以认为降噪效果更好。均方根误差是很好衡量一种评价数据变化程度的参数,在降噪中用来表征降噪后的信号与纯信号的差异,当均方根误差越小则表明降噪后的信号越接近纯信号。降噪后能量占原信号能量百分比则可以用来观测信号降噪过度与否。信噪比SNR、均方根误差RMSE、能量比Esn如式(5)、式(6)、式(7)所示。

式中,yi表示原始信号；xi表示经过降噪后的信号；N 表示数据的长度。

4 仿真数据降噪分析

该文分别从多频叠加的信号来模拟检测降噪效果。多频叠加信号y(t)各分量如式(8)所示。其采样频率取为2 000 Hz,分别在纯信号上添加上5 db和10 db的高斯白噪声。纯信号单边谱图、时域图和含不同信噪比噪声图如图1、图2所示。

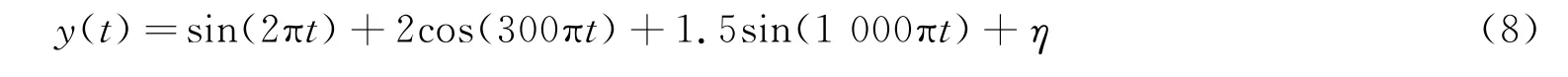
式中,η为白噪声信号。

从图2可以很清楚的看出来当信噪比越小的时候,信号将会变得更加模糊无规律,突刺更多,被噪声影响更明显。证明信噪比是越大越好。通过对含噪5 db信号降噪结果来对比分析EMD 降噪和小波降噪的优劣。小波分解时,由于所选的多频叠加信号是连续性很好得信号,故该文选择sym8小波基,分解层数经过多次调试取为6层,选用误差较小的Rigusure阈值准则和软阈值法。而其中EMD 分解后生成9个IMF,各阶IMF如图3、图4、图5所示。

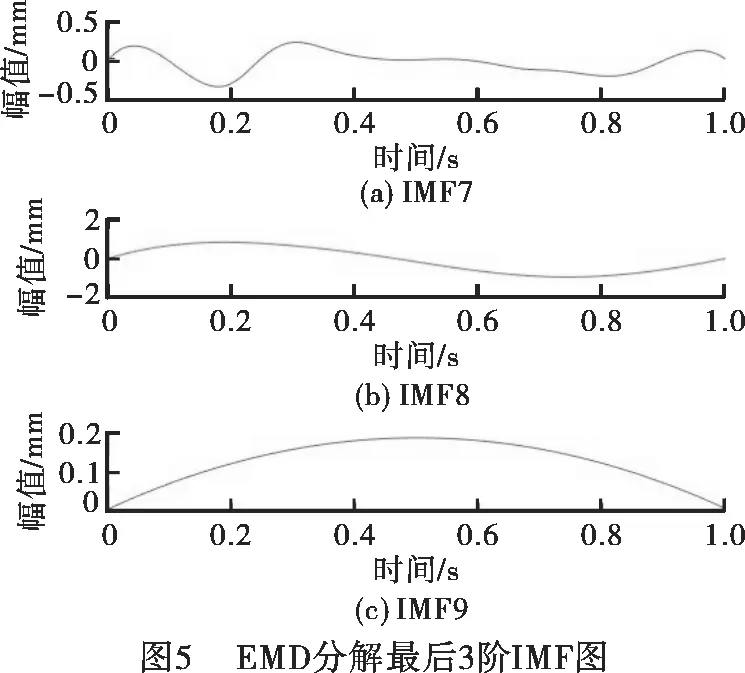
根据EMD 分解图可以清楚的看到IMF1为高频的噪声成分,应该将其去除,可以看到IMF2分解出了原始信号中的高频部分,但对于低频来说,出现了较严重的模态混叠,尤其是IMF3、IMF4、IMF5。将IMF1去掉再重组,得到如图6所示的EMD 降噪后的信号。而小波分解降噪重构的信号如图7所示。

表1 降噪效果对比

从表1中降噪效果对比可以知道小波降噪和EMD 降噪相差不多,小波降噪效果略好于EMD。

5 结 语

该文分别运用了EMD 和小波分解对多频叠加信号进行分解重构从而实现降噪。从信噪比、均方根误差、以及降噪前后能量比三个性能指标对比,发现对于该模拟信号,小波降噪效果要优于经验模态分解,但是优势不太明显。但小波选择不同的阈值准则以及不同的小波基均会产生不同的结果,而EMD 作为自适应分解的算法,相对于小波更加清晰明了,方便快捷,不需要选取小波基和阈值。