铝合金插铣加工切削力分析及成屑弧区划分研究
2020-06-08周井文秦文津2任培强
周井文,秦文津2,任培强
(1.上海航天精密机械研究所,上海 201600;2.上海航天智能装备有限公司,上海 201112)
当前航空航天产品为满足轻量化需求和结构强度、装配精度等指标,绝大部分采用深腔、减重槽框和空心薄壁等整体结构,例如整体叶盘、壁板、桁架等。由于极大的材料去除量和典型的弱刚性结构特点,采用传统加工方式及加工工序存在加工效率低、刀具系统刚度差、加工难度大等一系列问题。基于这一现状,近年来国内外学者提出了高速插铣加工方式。插铣加工又称为Z轴铣削法,即在数控加工过程中,刀具沿刀轴方向直线进给,利用底部的切削刃进行钻、铣组合切削[1],这是一种能够在Z方向上快速去除大量金属的加工方式,主要用于粗加工和半精加工。刀具在重复插铣达到预定深度时,不断地缩回和复位以便于下一次插铣时可快速地从重叠走刀处去除大量金属[2]。与传统的侧铣加工相比,插铣加工能降低刀具的径向切削力,使切削力保持稳定[3]。
目前,插铣加工的研究方向主要可以分为插铣动力学研究、加工模态分析、工艺技术等方面。Li 等[4]研究并提出了复杂型面插铣模型并且预测了铣削力的大小,但并未考虑系统的动态结构的影响。Damir 等[5]就柔性和刚性工件系统的条件下研究插铣力和插铣振动。赵伟[6]分析了高速插铣加工的稳定性,并从理论粗糙度、切削速度和切削振动的角度分析加工表面粗糙度,从而建立插铣加工的表面粗糙度模型。Altintas等[7–9]研究了插铣加工过程的动力学与稳定性,建立插铣加工时域仿真模型,该模型在考虑刀具的切削误差和时间变量参数的影响的基础上,对切削力、扭矩、振动做出预测,并且建立颤振稳定性图。
本文采用正交试验,研究了刀具转速、每齿进给量和径向切宽对切削力的影响规律,并对切削力信号进行了快速傅里叶(FFT)变换,分析了切削加工稳定性。同时建立了刀具切削角与瞬时切削力的关系,研究了切削力系数随每齿切削材料面积的变化规律。
试验及方法
试验在车间DMG Mori 1035V三轴加工中心上进行(图1(a)),机床最大转速为12000r/min,主轴最大功率为17kW,X/Y/Z方向行程分别为1035mm/560mm/530mm。切削力测量系统为Kistler 9253B23 多分量测力仪、Kistler 5070A 电荷放大器(图1(b))以及相应的数据采集与处理系统。测力仪基本参数为灵敏度0.05N;量程为±12kN(X,Y),–12~25kN(Z),±200N·m(扭矩);三向测力方向如图1(b)所示。试验刀具为机夹式刀具,直径为25mm,齿数为2。刀片无涂层,后角为21°,刀尖圆角为0.8mm。刀片侧刃长度为11mm(图1(c))。
试验采用基于刀具转速N、每齿进给量fz和径向切宽ae的3 因素3水平正交试验,具体加工参数见表1。试验材料为典型2A12 硬铝合金锻件。
结果与讨论
1 切削力方差分析
对切削力Fx、Fy和Fz进行方差分析(ANOVA),具体如表2~4 所示。以Sign.<0.1 作为显著性依据,可以认为只有每齿进给量fz和径向切宽ae是影响切削力Fx的显著因素,其余均不是显著因素。

图1 加工条件及加工刀具Fig.1 Experimental setup and cutting tools

表1 各加工参数因素水平及实测切削力Table1 Factors of each machining parameter and measured cutting force

表2 Fx方差分析表Table2 Analysis of variance of Fx
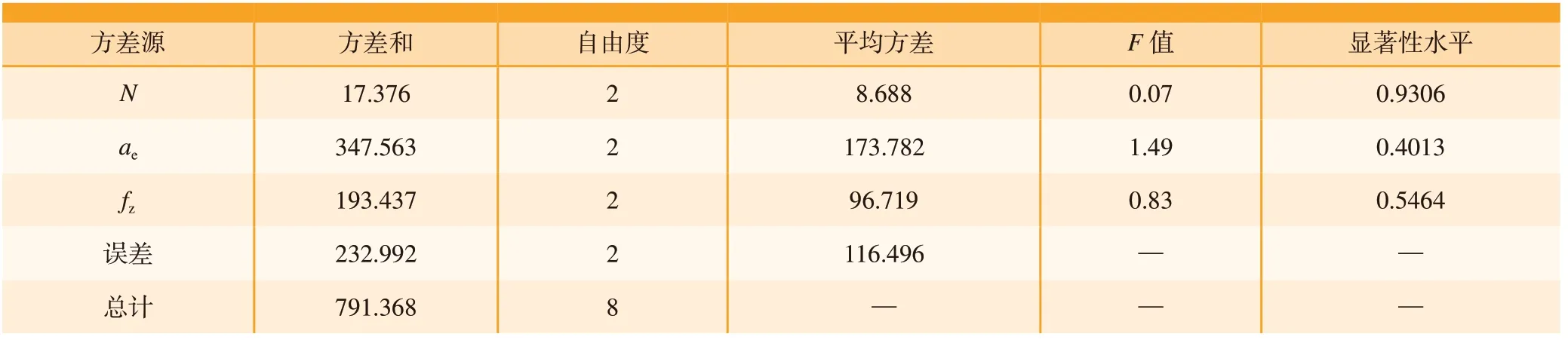
表3 Fy方差分析表Table3 Analysis of variance of Fy

表4 Fz方差分析表Table4 Analysis of variance of Fz
基于三向切削力Fx、Fy和Fz的平均值建立基于刀具转速N、每齿进给量fz和径向切宽ae的多元线性回归方程(式(1)~(3))。可以发现对于切削力Fy和Fz,由于其方程相关系数非常低,切削力信号离散而无规律。对于切削力Fy可以发现每齿进给量fz和径向切宽ae在方程中指数远大于刀具转速N,复合方差分析结果。对切削力原始信号进行时频域转换,具体如图2所示。当刀具转速N为6000r/min 时,测力信号的主频如式(4)所示应为200Hz,次频为100Hz 和300Hz。可以发现对于切削力Fx,信号稳定且主频振幅最大,远大于其他频率。800Hz 频率振幅同样很大,同时为主频的整数倍,可以认为是加工过程中的振动所致,同时也符合前文方差分析中刀具转速的显著性影响非常低的结论。然而对于切削力Fy和Fz,可以发现主频在频谱图中振幅已不占主要,即使排除次频仍然存在大量其他频率振幅。说明在加工过程中刀具在y方向和z方向存在较多低频振动,这一现象也印证了前文的多元线性回归方程拟合相关性非常低的问题。
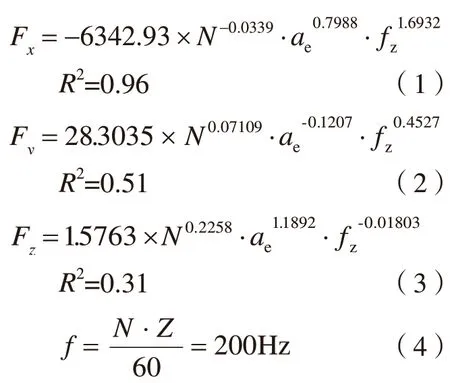
结合前文分析,可以得到切削力Fx随每齿进给量fz和径向切宽ae变化趋势,具体如图3所示,可以发现切削力Fx在选定参数区间内随每齿进给量fz和径向切宽ae的增大而稳定增大。
2 切削成屑弧区划分及分析
图4为典型插铣加工刀具每齿运动轨迹示意图,可以发现瞬时实际每齿切厚ae'是随刀具转角φ呈现先增大(0°<φ<90°)后减小(90°<φ<180°)的趋势。实际瞬时每齿切厚ae'是不等于预设轴向切宽ae的,具体关系如式(5)所示。依照海伦公式和三角形两边一内角的面积公式,消去公共面积变量三角形面积即可。
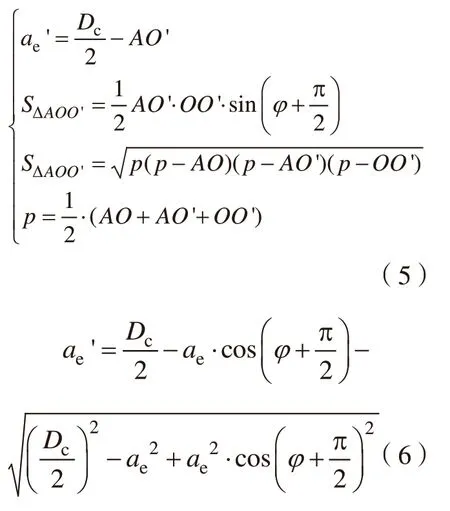
式中,ae' 为实际每齿切厚;ae为径向切宽;φ为刀具转角;Dc为刀具直径,本试验默认为25mm。需要指出的是刀具直径25mm 为插铣刀具直接中位数(一般插铣刀在16~60mm 之间),具备一定代表性,且随着刀具直径Dc的增大,实际每齿切厚ae'将随之减小,但是在刀具直径范围内其变化幅度非常细微,暂不讨论。
实际每齿切厚ae' /径向切宽ae随刀具转角φ变化趋势具体如图5所示,可以发现实际每齿切厚ae' 在刀具转角φ=90°时达到最大值,等于径向切宽ae,在刀具切入/切出阶段,实际每齿切厚ae' 最小。
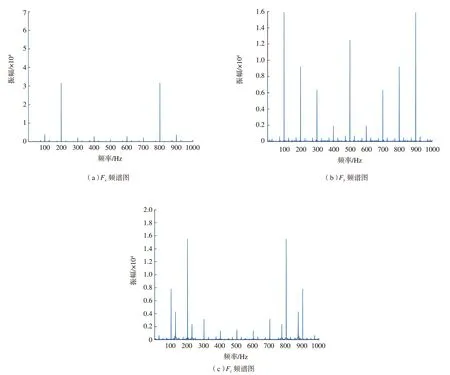
图2 三向切削力频谱分析(N=6000r/min,fz=0.06mm/z,ae=1mm)Fig.2 Spectral analysis of cutting forces (N=6000r/min,fz=0.06mm/z,ae=1mm)
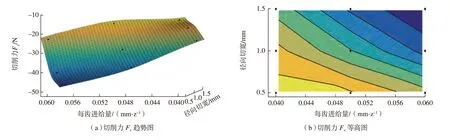
图3 每齿进给量fz和径向切宽ae对切削力Fx的影响Fig.3 Influences of feed rate and radial cutting width on cutting force Fx
基于以上分析,可以计算每齿所切削材料的截面积S',具体见式(7)。

其中,fz为插铣加工每齿进给量。
基于图5同样可以认为每齿所切削材料的截面积S'与实际每齿切厚ae'具有同样规律,在此不再赘述。
图6所示为切削力Fx和Fy随时间变化规律,可以发现切削力Fx的波形规律性要明显优于切削力Fy的波形,这与之前的分析也能够完全吻合(试验序号5)。将图6的关系按照式(8)转化为随刀具转角φ的变化规律,具体如图7所示,可以发现切削力Fx具有非常强的规律性,而切削力Fy规律性较差。结合图4可以发现对于切削过程中切削力Fx和Fy仅为法向切削力Fn和切向切削力Ft合成而成,两者之间的关系为
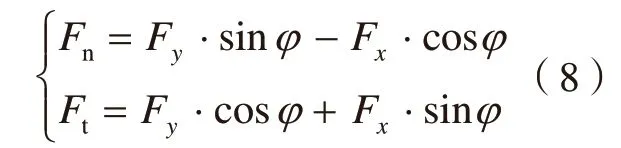
结合图8(a)可以发现,对于切向切削力Ft,其大小随刀具转角φ呈现对称分布,且在φ=90°时达到最大值,当φ=20° 和160° 时 可以发现明显的低谷。当刀具转角φ在0~20° 和160°~180° 范 围 内,由于最小切厚理论,此时刀具并没有切除材料。一是由于过小的切厚导致材料受力发生弹性变形退让;二是由于刀具刃口圆角的存在,使得被去除材料受刃口圆角的挤压并没有被去除。在这一阶段刀具后刀面仅是在加工表面发生挤压,并不成屑。当刀具转角φ在20°~90°和160°~90°范围内时,根据金属切削理论,随着瞬时切厚ae' 的不断增大,意味着在刀具前刀面(即第1 变形区)发生剪切滑移变形的材料厚度不断增加,这导致了切向切削力Ft的不断增大。
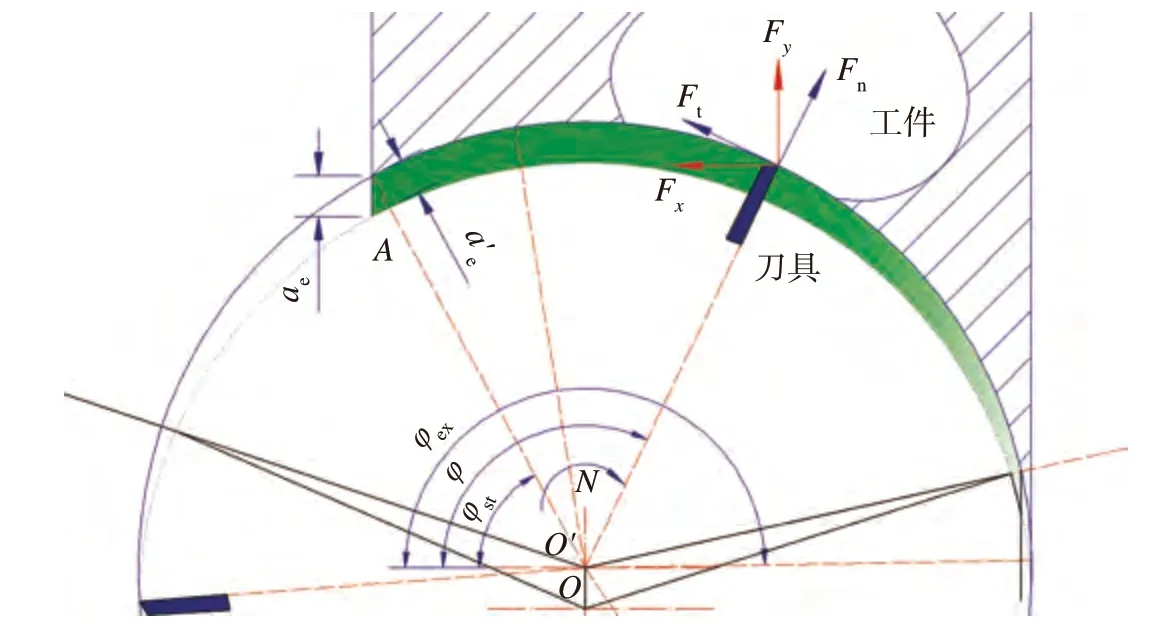
图4 插铣加工刀具每齿运动轨迹示意图Fig.4 Diagram of cutting edge movement

图5 刀具转角φ对实际每齿切厚ae'/径向切宽ae的影响Fig.5 Influences of tool engage angle φ on actual chip thickness ae'/ radial cutting width ae

图6 切削力Fx和Fy随时间变化规律Fig.6 Cutting forces Fx and Fy vs time
对法向切削力Fn分析可以发现,切削力整体相对于φ=90°对称(图8(b))。在于在刀具转角φ=45°和135°时法向切削力Fn达到最大值,并且在0~45°和180°~135°范围内,法向切削力Fn不断增大。结合上文的分析可以得到在这一区域属于材料回弹区域,并且回弹随着瞬时切厚ae'的增大而不断加剧。同时可以发现在20°~45°和160°~135°范围内,属于刀具后刀面与工件材料作用的过渡区域,在这一区间属于从挤压阶段向切削阶段的转变区域,属于划擦区域。可以发现当刀具刃口真正开始切除材料时(即φ=45°~135°),工件材料对刀具后刀面的挤压回弹作用反而减轻,此时材料主要在刀具前刀面发生剪切滑移变形,具体如图9所示。
结论
本文利用铝合金插铣加工正交试验,从工艺角度分析了刀具转速N、每齿进给量fz和径向切宽ae加工参数对三向切削力的影响规律,并进行了方差显著性分析(ANOVA),建立了关于加工参数的多元线性回归方程,讨论了加工过程振动对切削力信号的影响。从切削理论角度建立了切削力与刀具转角、瞬时每齿切厚的理论计算关系。基于切向/法向切削力的变化规律,将切削弧区划分为挤压区、划擦区和切削区。具体结论如下:
(1)每齿进给量fz和径向切宽ae均是影响切削力Fx的显著因素;
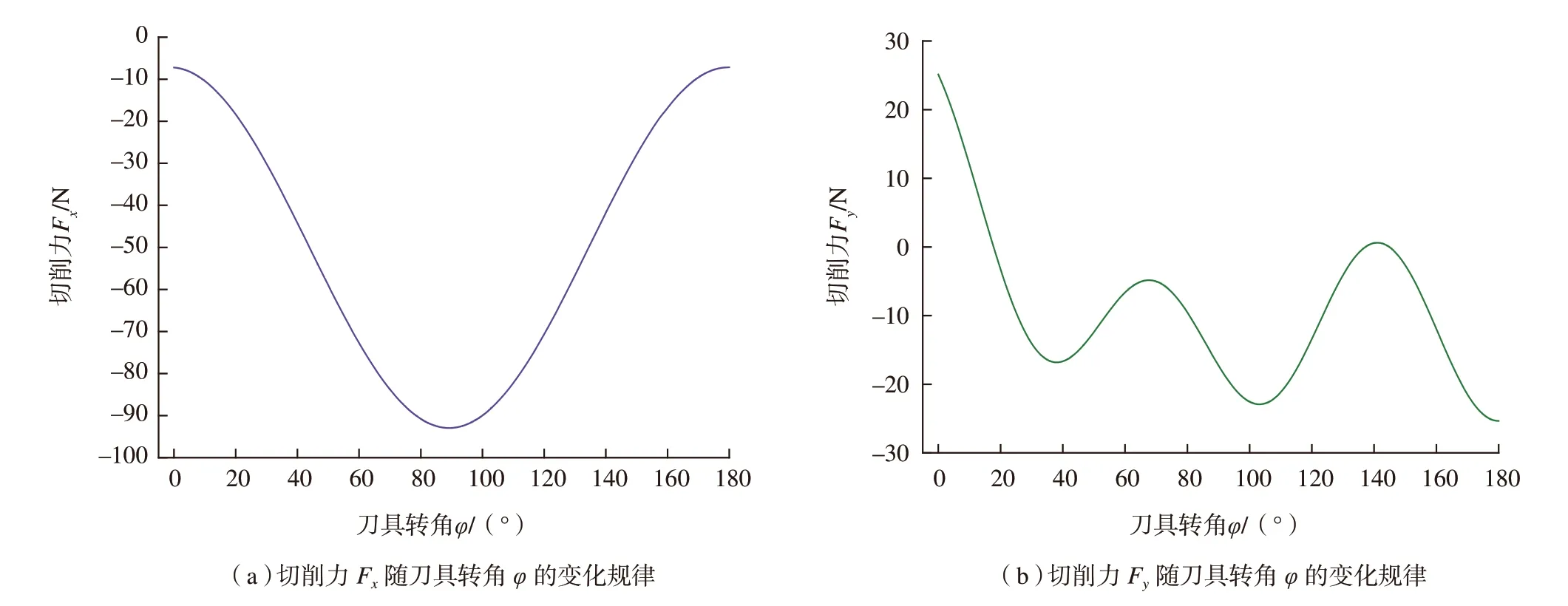
图7 切削力Fx和Fy随刀具转角φ的变化规律Fig.7 Cutting forces Fx and Fy vs tool engage angle φ

图8 切削力Ft和Fn随刀具转角φ的变化规律Fig.8 Cutting forces Ft and Fn vs tool engage angle φ
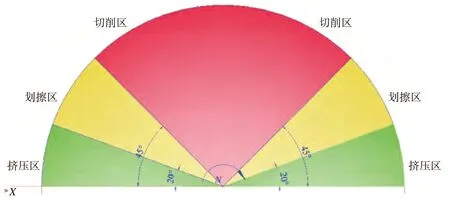
图9 切削成屑弧区划分Fig.9 Partition of chip-forming area
(2)切削力Fx最为稳定,x方向加工过程中无振动。而切削力Fy和Fz信号随机误差较大,y方向和z方向加工过程不稳定,存在较多低频振动;
(3)切削弧区按照刀具转角φ可以划分为3 个区域。
区域1:0~20°(160°~180°)范围内,刀具仅仅在材料表面挤压滑行,并不成屑。
区域2:20°~45°(135°~160°)范围内,刀具在材料表面发生划擦,属于从挤压滑行向切削成屑转变的过渡阶段。在这一范围内既有刀具后刀面与材料的回弹挤压作用,也有材料受刀具前刀面的剪切成屑作用。
区域3:45°~135°范围内,材料主要发生剪切滑移变形,属于正常切削过程。
