基于响应面的波形钢腹板PC组合梁桥有限元模型修正方法的试验研究

2020-06-08康志锐张巍宋帅张进标

铁道科学与工程学报 2020年5期

康志锐，张巍，宋帅，张进标

康志锐，张巍，宋帅，张进标

(太原理工大学土木工程学院，山西太原 030024)

为探讨波形钢腹板PC组合箱梁桥模型修正方法应用于实桥结构运营安全性能评估的有效性，开展实桥荷载试验，并基于响应面法，以设计参数为自变量，利用竖向前3阶自振频率构造目标函数进行迭代优化，从而实现对有限元模型的修正，使修正后模型的计算结果和试验实测值的偏差在合理范围内。而后按照静载试验的加载工况对有限元模型加载，通过对比挠度计算值与试验值，验证其精确性。研究结果表明：修正后的模型能够真实反映桥梁的实际运营状态，可以作为该桥的基准有限元模型用于桥梁运营安全性能评估。

组合箱梁桥；波形钢腹板；响应面法；动静载试验；模型修正

波形钢腹板PC组合箱梁桥是一种新型的钢−混凝土组合结构型式，用波形钢腹板代替传统的预应力混凝土箱梁的混凝土腹板，从而减轻了箱梁的自重，并且有效地解决了预应力混凝土箱梁腹板开裂的问题，因此得到较多的推广和应用。据相关统计数据显示，到2015年底，国内已经建成及正在修建的该类型桥梁已经超过70座[1]。当前，基于有限元模型修正方法评估桥梁运营安全性能的研究取得了显著进展。以实桥荷载试验数据为基准，对依据桥梁设计图纸建构的初始有限元模型进行设计参数显著性分析和修正，使修正后的有限元模型能够真实地表征桥梁结构当前的运营状态，为评估桥梁的运营安全性能提供了有效的技术手段。田仲初等[2]分别运用静测和动测数据对佛山东平大桥进行模型修正，结果表明修正后的有限元模型可以准确地反映桥梁的静动力特性。邬晓光等[3]利用灵敏度权重系数和动态系数，结合联合静动力有限元修正方法对一曲线梁桥进行修正，使各目标响应计算结果与实测值之间的误差明显减小。宗周红等[4]利用响应面法对连续刚构桥进行模型修正，修正后的模型竖向频率和横向频率计算结果与实测值相差小于10%。韩建平等[5]采用2种试验设计方法对刚构−连续组合梁桥进行模型修正，发现采用不同试验设计对修正后模型的计算结果影响很小。何涛等[6]将动态加权系数与灵敏度分析方法相结合，并联合动静力目标函数对预应力混凝土梁的有限元模型进行修正，使修正后模型的计算精度显著提高。赵崇基等[7]结合动力测试对混凝土连续梁桥进行模型修正，并应用于桥梁运营阶段承载力的评估中。张挣鑫等[8]利用响应面技术对拱桥进行有限元模型修正，使修正后的有限元模型计算结果的误差满足实际使用的要求。李延强等[9]基于结构参数对一座独塔斜拉桥进行模型修正，经修正后的有限元模型索力、位移计算值与实测值吻合良好。上述研究表明，有限元模型修正方法在拱桥、斜拉桥、刚构桥和预应力混凝土连续梁桥的静、动力特性分析及承载力评估中得到较多应用，但是针对波形钢腹板PC组合箱梁桥模型修正方法的研究目前国内开展的还较少。随着该桥型结构的广泛推广和应用，急需对波形钢腹板PC组合箱梁桥的模型修正方法展开深入研究，探讨该桥型结构模型修正方法的有效性和适用性，为该桥型结构的设计、施工和运营安全性评估提供可靠的分析方法。

1 响应面法模型修正的基本原理

基于响应面法进行模型修正的本质在于：通过响应面拟合获得响应面模型来代替有限元模型进行计算，得到最优期望值，从而有效地克服直接利用有限元模型进行修正过程中迭代次数过多、计算量过大的缺点。其基本设想为：首先，运用试验设计方法得到设计参数的试验组合，通过有限元模型计算相应试验组合的自振频率；其次，对设计参数进行参数筛选，基于筛选后的设计参数利用多元回归法构建响应面模型；最后，利用响应面模型进行约束优化求解，获得使模型计算结果与实桥试验结果最符合的设计参数，实现对有限元模型的优化，总体流程如图1所示。

图1 基于响应面法的模型修正方法流程图

1.1 试验设计

试验设计是运用数理统计的原理，按照相应的试验目的制定合适的试验方案，使试验在较少的样本点和试验次数下达到较高的精确度，常用的试验设计有：BBD设计、正交设计、均匀设计和中心复合设计等[10]。本文选用的是D-最优设计(D-Optimal Design)，其样本点选取不对称，因而在大幅减少试验次数的同时能有效评估模型的精度[11]。

1.2 参数筛选

参数筛选即筛选出对自振频率计算结果影响显著的设计参数。通过运用F检验法进行方差分析，判断参数的显著性水平，从而克服了以往灵敏度分析方法仅计算局部灵敏度的缺点[12−13]，表达式如下：

式中：SSA为因素引起的偏差平方和；SSE为试验误差引起的偏差平方和；f为各因素的自由度；f为试验误差的自由度。

通过计算出统计量的显著水平值，筛选出所有设计参数中对有限元模型自振频率计算结果影响显著的设计参数，并将这些参数作为状态变量进行修正。

1.3 响应面拟合

响应面拟合就是运用回归分析技术将筛选出的设计参数与自振频率计算结果之间复杂的隐式关系用简单的显示函数表达，从而建立响应面模型[14−15]。常用的响应面模型为二次多项式，形式如下：

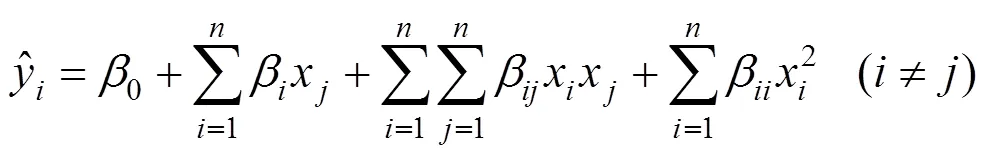
同时，引入复相关系数2和相对均方根误差RMSE对响应面拟合的精确性进行检验，计算公式如下：

1.4 目标函数

本文以设计参数作为自变量，以响应面模型计算的桥梁竖向前3阶自振频率值与试验实测的竖向前3阶自振频率值的相对偏差不超过10%作为约束条件构造目标函数。其表达式如下：

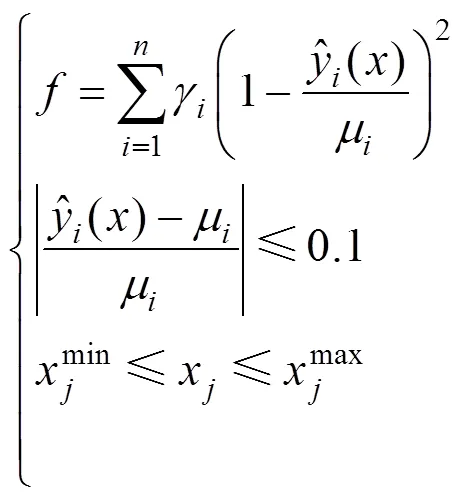
2 波形钢腹板PC组合箱梁桥实桥试验简介

2.1 桥梁概况

本文以某城市道路高架桥为研究对象，该桥为单箱三室波形钢腹板PC组合箱梁桥，桥跨结构跨径组合为35+2×40+35 m，桥面宽(0.5 +15 +0.5) m，梁高2.5 m。箱梁的顶、底板的材料采用C55混凝土，波形钢腹板的钢材型号为Q345D，设计时速为40 km/h，设计荷载为城-A级。桥墩的型式为双肢花瓶墩，基础为桩基。桥梁结构总体布置见图2，上部结构横截面如图3所示。

2.2 实桥试验简介

实桥试验分为静载试验和动力试验2部分。静载试验在该桥的第1跨和第2跨的/4，/2及3/4处的下缘分别布置位移传感器，测试在静载作用下主梁的挠度。其加载方式为：纵桥向选用十辆平均重量为336.9 kN的载重汽车，按照各控制截面弯矩影响线进行最不利布载；横桥向的布载方式为对称布载和偏心布载。动载试验采用脉动激励试验方法，运用大容量数据自动采集仪和信号处理分析系统，采集和分析波形钢腹板PC组合箱梁桥在无荷载状况下的自由振动响应信号，确定桥梁结构的自振特性参数。

单位：cm

3 波形钢腹板PC组合箱梁桥初始有限元模型及模型修正

3.1 初始有限元模型

本文采用ANSYS有限元软件对波形钢腹板PC组合箱梁桥进行建模。混凝土顶底板采用Solid65单元模拟，普通钢筋通过输入体积配筋率模拟；波形钢腹板采用Shell63单元模拟，体内预应力钢绞线采用Link8单元模拟，并采用降温法施加预应力。波形钢腹板与混凝土顶底板的连接采用刚性连接，预应力钢束与混凝土的固结采用耦合节点自由度的方法实现，有限元模型如图4。

选取对桥梁结构自振频率影响较大的混凝土弹性模量、混凝土密度、钢腹板弹性模量和钢腹板泊松比作为待修正的设计参数，有限元模型的初始设计参数取值如表1。

表1 设计参数初始值

3.2 初始有限元模型自振频率计算结果与试验结果对比

在初始设计参数下有限元模型的竖向前3阶自振频率的计算结果、动力试验实测频率数据及两者的偏差见表2。

表2 初始有限元模型前3阶自振频率计算结果与试验结果对比

由表(2)可知，初始有限元模型的计算结果和实桥试验结果有较大偏差，最大偏差达到16.1%。这表明基于初始设计参数的有限元模型不能准确地反映波形钢腹板PC组合箱梁桥的真实动力特性，因此对初始有限元模型进行模型修正是十分必要的。

(a) 参数对竖向第1阶频率的显著性；(b) 参数对竖向第2阶频率的显著性；(c) 参数对竖向第3阶频率的显著性

3.3 响应面模型及精度检验

运用D-最优设计对待修正参数进行试验设计，得到38组不同的试验设计组合，并将其作为样本点，通过初始有限元模型计算不同试验组合对应的前3阶自振频率。根据式(1)对设计参数进行筛选，选取显著性水平=0.05，若值大于，则说明此参数的变化对有限元模型的频率计算结果没有显著的影响；反之，则说明此参数对计算结果的影响是显著的，需将其作为响应面模型中的设计参数进行修正。图5即为初始有限元模型中4个设计参数及其组合对波形钢腹板PC组合箱梁桥有限元模型竖向前3阶频率计算结果的显著性水平。

图中，横坐标为各参数及其组合，其中：A代表混凝土弹性模量；B代表混凝土密度；C代表钢腹板弹性模量；D代表钢腹板泊松比。纵坐标为各参数及组合的显著水平值。

由图5可知，对于波形钢腹板PC组合箱梁桥，除了交叉项AD和二次项AA和DD外，其它设计参数对竖向前3阶频率的影响都是显著的，且对各阶频率有显著影响的设计参数的种类是相同的。

在此基础上，利用式(3)和式(4)对响应面模型进行精确度检验，检验结果见表3。

表3 响应面模型的精确度检验

由表(3)可见，各个响应面模型的2都接近1，RMSE都接近0，说明其有足够的精度来代替有限元模型进行计算。

3.4 基于响应面的模型修正

模态频率作为桥梁运营状态监测的重要数据，通常由实桥试验获得。采用环境激励对桥梁结构进行模态频率采集，不需要封闭交通，实测方法简单，数据比较稳定可靠。因此，本文利用波形钢腹板PC组合箱梁桥的竖向前3阶自振频率构建目标函数对桥梁的有限元模型进行修正。目标函数见式(5)，权重系数取=1/3(=1,2,3)，在取值范围内对目标函数进行迭代求解，得到的最优解作为修正值。各设计参数的取值范围及修正值见表4。

表4 各设计参数的取值范围及修正值

由表4可以看出，修正后的混凝土密度比初始值增大了49.0%。这一方面是由于受施工过程中混凝土配合比、浇筑施工工艺等的影响，致使混凝土密度与设计图纸取值存在偏差；另一方面，建模过程中略去了对构造复杂的预埋钢连接件的建模，将混凝土顶、底板与钢腹板直接刚性连接，通过修正混凝土的密度来间接表征混凝土顶、底板与预埋钢连接件的质量，这也是导致混凝土密度修正值与初始值偏差较大的原因。

波形钢腹板修正后的泊松比相较初始值增大30.11%，这是由于波形钢腹板在构造上的正交异性，引起波形钢腹板在3个弹性主轴上的变形性能差异和相互影响，而建模中用一个泊松比来简化这种力学行为所导致。

3.5 修正前后有限元模型的动力计算结果对比

将模型修正后的设计参数输入有限元模型中，并且再次对波形钢腹板PC组合箱梁桥的竖向前3阶频率进行计算，结果如表5所示。

表5 修正后前3阶自振频率有限元模型计算结果与试验对比

对比表2与表5可发现，通过修正设计参数，有限元模型的自振频率计算结果与实桥试验实测数据的偏差较初始设计参数明显减小，修正后的有限元模型将更加准确地反映桥梁的动力特性。

3.6 修正前后有限元模型的静力计算结果对比

本文针对基于自振频率修正的有限元模型静力计算结果的精确性进行探讨。依据实桥静力荷载试验的加载工况对修正前后的有限元模型进行加载，并将有限元模型的挠度计算结果与实桥试验的实测挠度进行对比，结果见表6。

表6 修正前后静载试验挠度计算结果与试验结果对比

对比表6修正前、后的偏差值可以看出：修正后有限元模型的挠度计算结果与实桥试验的实测结果偏差小于10%，且两者之间偏差的总体趋势是减小的。这表明经过自振频率修正后的有限元模型在受力变形上的计算精度有所提高。

4 结论

1) 本文采用实测的竖向前3阶自振频率，基于响应面法对一座波形钢腹板PC组合箱梁桥实桥进行模型修正。对比动静载试验结果表明，经过修正后的有限元模型的计算精度有所提高，能够作为基准有限元模型分析实桥结构的真实力学行为。

2) 研究表明，混凝土弹性模量和密度、钢腹板弹性模量和泊松比的取值对有限元模拟分析波形钢腹板PC组合箱梁桥的动、静力响应具有显著影响，需要通过参数修正以逼近真实值。

3) 基于响应面法，以设计参数为修正对象，利用频率实测值构造目标函数，对波形钢腹板PC组合箱梁桥有限元模型进行修正的方法简便可靠、计算工作量小、精度高，对该类型桥梁的运营安全性能评估具有参考价值。

[1] 李宏江. 波形钢腹板PC组合箱梁动力性能研究综述[J]. 建筑钢结构进展, 2018, 20(4): 75−84.LI Hongjiang. Review of research on dynamic performance of pc composite box girder with corrugated steel webs[J]. Progress of Building Steel Structure, 2018, 20(4): 75−84.

[2] 田仲初, 彭涛, 陈政清. 佛山东平大桥静动力分层次有限元模型修正研究[J]. 振动与冲击, 2007, 26(6): 162− 165.TIAN Zhongchu, PENG tao, CHEN Zhengqing. Research on the modification of static and dynamic layered finite element model of foshan dongping bridge[J]. Journal of Vibration and Shock, 2007, 26(6):162−165.

[3] 邬晓光, 刘英, 冯宇, 等. 基于动态系数的静动力有限元模型修正研究[J]. 铁道科学与工程学报, 2017, 26(6): 162−165.WU Xiaoguang, LIU Ying, FENG Yu, et al. Static and dynamic finite element model correction based on dynamic coefficient[J]. Journal of Railway Science and Engineering, 2017, 26(6):162−165.

[4] 宗周红, 高铭霖, 夏樟华. 基于健康监测的连续刚构桥有限元模型确认(Ⅰ)——基于响应面法的有限元模型修正[J]. 土木工程学报, 2011, 44(2): 90−98.ZONG Zhouhong, GAO Minglin, XIA Zhanghua. Based on the finite element model of continuous rigid frame bridge health monitoring confirmed (Ⅰ)-based on response surface method, finite element model of correction[J]. Journal of Civil Engineering, 2011, 44(2): 90−98.

[5] 韩建平, 骆勇鹏. 基于响应面的刚构−连续组合梁桥有限元模型静动力修正[J]. 公路交通科技, 2013, 30(11): 53−61.HAN Jianping, LUO Yongpeng. Static and dynamic modification of finite element model of rigid structure-continuous composite beam bridge based on response surface[J]. Highway Traffic Science and Technology, 2013, 30(11): 53−61.

[6] 何涛, 张巍, 吴植安. 基于动静载试验数据的预应力混凝土梁模型修正方法试验研究[J]. 公路交通科技, 2015, 32(12): 75−80.HE Tao, ZHANG Wei, WU Zhian. Experimental research on model correction method of prestressed concrete beam based on static and static load test data[J]. Highway Traffic Science and Technology, 2015, 32(12): 75−80.

[7] 赵崇基, 张巍, 刘志华, 等. 基于动力测试的混凝土连续梁桥有限元模型修正[J]. 广西大学学报(自然科学版), 2016, 41(4): 1264−1270.ZHAO Chongji, ZHANG Wei, LIU Zhihua, et al. Finite element model modification of concrete continuous beam bridge based on dynamic test[J]. Journal of Guangxi University (Natural Science Edition), 2016, 41(4): 1264− 1270.

[8] 张挣鑫, 刘黔会, 黄方林. 面向桥梁工程的响应面技术在有限元模型修正中的应用探讨[J]. 公路工程, 2018, 43(4): 145−149.ZHANG Zhengxin, LIU Qianhui, HUANG Fanglin. Discussion on the application of response surface technology for bridge engineering in finite element model modification[J]. Highway Engineering, 2018, 43(4): 145− 149.

[9] 李延强, 杜彦良, 符强. 基于实测索力的模型斜拉桥有限元模型修正研究[J]. 铁道学报, 2013, 35(6): 91−95. LI Yanqiang, DU Yanliang, FU Qiang. Finite element model modification study of cable-stayed bridge model based on measured cable force[J]. Journal of the China Railway Society, 2013, 35(6): 91−95.

[10] 李莉, 张赛, 何强, 等. 响应面法在试验设计与优化中的应用[J]. 实验室研究与探索, 2015, 34(8): 41−45.LI Li, ZHANG Sai, HE Qiang, et al. Application of response surface method in test design and optimization [J]. Laboratory Research and Exploration, 2015, 34(8): 41−45.

[11] 朱跃, 张令弥, 郭勤涛. 基于SVR方法的有限元模型确认中不确定性建模研究[J]. 振动与冲击, 2010, 29(9): 119−122.ZHU Yue, ZHANG Lingmi, GUO Qintao. Uncertain modeling research on finite element model confirmation based on svr method[J]. Journal of Vibration and Shock, 2010, 29(9): 119−122.

[12] FANG S E, Perera R. A response surface methodology based damage identification technique[J]. Smart Materials & Structures, 2009, 18(6): 065009.

[13] REN W X, CHEN H B. Finite element model updating in structural dynamics by using the response surface method[J]. Engineering Structures, 2010, 32(8): 2455− 2465.

[14] 韩伟, 何景武. 响应面拟合法在机翼结构优化中的应用研究[J]. 飞机设计, 2013, 33(5): 6−11.HAN Wei, HE Jingwu. Application research of response surface fitting method in wing structure optimization[J]. Aircraft Design, 2013, 33(5): 6−11.

[15] 潘晓磊, 王家群, 胡丽琴,等. 基于响应面拟合方法中国铅基研究实验堆非能动余热排出系统可靠性分析[J]. 核技术, 2016, 39(5): 67−72.PAN Xiaolei, WANG Jiaqun, HU Liqin, et al. Reliability analysis of passive waste heat removal system of China lead-based research experimental reactor based on response surface fitting method[J]. Nuclear Technology, 2016, 39(5): 67−72.

Experimental research on FE model updating of PC composite box girder bridge with corrugated steel webs based on response surface method

KANG Zhirui, ZHANG Wei, SONG Shuai, ZHANG Jinbiao

(College of Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

To explore the effectiveness of FE model updating method in safety performance assessment of PC composite box girder bridge with corrugated steel webs, the dynamic and static load test of bridge was carried out. On base of the response surface method, taking the design parameters as independent variables, the first three natural frequencies was used to construct the objective function for iterative optimization. So that the deviation between calculation results of FE model and values of load test is within a reasonable range. Then, according to the loading condition of the static load test, the finite element model was loaded, and the accuracy was verified by comparing the calculated value of the deflection with the experimental value. The results show that the modified model can truly reflect the actual operational status of the bridge, and can be used as the baseline FE model of the bridge for the safety performance evaluation of bridge operations.

composite box-girder bridge; corrugated steel web; response surface method; dynamic and static load test; model updating