深厚砂层地下连续墙槽壁稳定性特征及影响因素研究
2020-06-08邱明明杨果林申权段君义张沛然
邱明明,杨果林,申权,段君义,张沛然
深厚砂层地下连续墙槽壁稳定性特征及影响因素研究
邱明明1,杨果林2,申权3,段君义2,张沛然2
(1. 延安大学 建筑工程学院,陕西 延安 716000;2. 中南大学 土木工程学院,湖南 长沙 410075;3. 湖南工业大学 土木工程学院,湖南 株洲 412007)
以深厚富水砂层地连墙成槽施工为研究背景,通过现场试验和数值模拟方法研究深厚富水砂层地连墙泥浆槽壁稳定性特征及其影响因素。研究结果表明:泥浆液面波动是诱发深厚富水砂层地连墙槽壁发生浅层失稳的重要原因,其失稳区域为导墙顶面下2.0~7.5 m范围的粉土层和砂性土层;槽壁水平变形沿深度方向呈上大下小的非对称“鼓肚”形曲线分布,地表竖向变形沿横向水平距离呈“勺子”形曲线分布,最大沉降值位置距槽壁水平距离约(0.10~0.15)e(e为成槽深度),沉降槽宽度约为(1.0~1.5)e;提高泥浆液面高度、降低地下水位、合理设置槽壁加固体间距均有利于深厚富水砂层地连墙成槽槽壁稳定。研究成果可为同类工程地连墙槽壁稳定性控制和施工参数优化提供参考。
地下连续墙;槽壁稳定;现场试验;数值模拟;影响因素
随着城市地下空间开发利用的深入发展,地下连续墙以其整体性强、刚度大、强度高、隔水性能好等优点被广泛应用于地下围护结构中,而在其成槽施工过程中,控制槽壁稳定是成槽顺利进行和确保地连墙施工质量的基础。但由于复杂地质条件、地下水位、施工工艺、周围环境等因素影响,易诱发槽壁发生滑塌、缩颈等失稳现象,对地连墙成槽施工安全和周围环境极为不利[1−3]。因此,在复杂的地质环境条件下如何控制槽壁稳定是地连墙成槽施工亟待解决的关键技术问题。目前,针对地连墙成槽槽壁失稳机制及其稳定性分析方法已开展了一定的研究工作,诸多学者主要采用理论分析法[4]、现场试验[5−6]、模型试验[7]、数值模拟[8]等方法从整体稳定性和局部稳定性方面对该问题进行了解答。DING等[9−10]对地连墙槽壁稳定影响因素、槽壁整体及局部失稳机制、不同施工阶段槽壁土体的应力路径进行了分析。ZHUO等[7]借助离心模型试验研究了不同类型泥浆对软土地层地连墙成槽施工槽壁稳定性的影响特征。HAN等[11]采用极限分析方法推导了黏性土层地连墙槽壁整体稳定性和局部稳定性安全系数的解析解。王启云等[12]基于极限平衡理论和强度等效原理,推导了深厚软弱地层加固槽壁的稳定安全系数计算公式,对比分析了槽壁稳定性影响参数,并提出了控制槽壁稳定的具体措施。缪圆冰等[13]采用极限分析理论和强度折减法,推导了槽壁局部稳定安全系数和临界高度计算公式,并对其随泥浆重度和夹层特性参数变化的影响规律进行了分析。崔根群等[14]建立了地连墙成槽施工槽壁稳定极限平衡力学模型,推导了槽壁稳定条件下的泥浆重度计算公式。朱宁等[2]借助FLAC3D程序建立了三维地连墙成槽施工力学模型,对粉土地层地连墙成槽施工对土体扰动变形及周边建筑物的影响规律进行了分析。综上所述,针对深厚富水砂层地质条件下地连墙槽壁稳定性及其影响因素的研究则少有报道。鉴于此,本文以某深基坑地连墙工程为研究背景,开展深厚富水砂层地连墙成槽现场试验,研究深厚富水砂层地连墙成槽施工槽壁稳定性特征,建立考虑渗流作用的地连墙成槽施工数值分析模型,对比分析地连墙槽壁稳定性影响因素,以期为同类地连墙槽壁稳定性控制和施工参数优化提供参考。
1 现场试验
1.1 工程概况
某地铁车站深基坑工程,基坑总长150.0 m,宽19.5~23.2 m,开挖深度约21.0~23.0 m,覆土厚度约2.5 m。基坑东、西、北侧三面环江河,水平距约30~300 m,南侧27.0 m处为高层住宅楼,周围环境较为复杂。基坑围护结构采用0.8 m厚地下连续墙(深度30.0 m),沿深度方向共设4道内支撑。根据车站工程地质详勘报告,场地地层为人工填土(Qml)、第四系全新统冲积层(Q4al)、下部为第三系新余群(Exn)基岩。按其岩性及其工程特性,自上而下依次划分为:①1杂填土,层厚0.5~1.9 m;②1粉质黏土,层厚0.7~2.8 m;②2粉土,层厚1.2~4.6 m;②3细砂,层厚2.4~7.3 m;②3−1砾砂,层厚1.1~5.8 m;②5粗砂,层厚2.5~7.8 m;②5−1淤泥质粉质黏土,层厚0.4 m;②6砾砂,层厚0.6~4.3 m;⑤1强风化泥质粉砂岩,层厚0.7~1.6 m;⑤2中风化泥质粉砂岩,层厚10.0~12.2 m;⑤3微风化泥质粉砂岩,最大揭露层厚13.2 m,见图1。基坑开挖深度范围内地下水含量比较丰富,埋深约3.4~9.6 m,主要为赋存于砂砾层中的孔隙潜水,水位变化受降雨和临近江水影响显著,水位年变幅1.0~3.0 m。

单位:m
1.2 试验方案设计
地连墙试验槽段幅长6.8 m,宽0.8 m,深30.0 m,采用SG60型全液压成槽机连续施工成槽,见图1(a)。试验段土层自上而下依次为0.7 m路面层、0.5 m杂填土层、2.8 m粉质黏土层、2.0 m粉土层、7.0 m细砂层、3.5 m砾砂层、2.0 m粗砂层、1.0m强风化泥质粉砂岩层、11.9 m中风化泥质粉砂岩层及微风化泥质粉砂岩。导墙为“┐┌”型现浇钢筋砼结构,厚度0.3 m,深度2.0 m,见图1(b)。试验泥浆采用高品质膨润土、纯碱、羧甲基钠纤维(CMC)和自来水为原材料混合配制而成,制备的新鲜泥浆性能指标为:黏度26.0 s,比重1.18 g/cm3,pH值9.0,含砂量1.5%,失水量8.5 mL/30 min。在成槽试验过程中,泥浆液面保持高出地下水位1.0 m以上,泥浆液面距导墙顶面距离的变化范围控制在0.3~1.0 m,且暂停施工时泥浆面不低于导墙顶面下0.3 m;现场抓斗提升速度控制在5~10 m/min,并根据泥浆液面变化及时向槽内补充泥浆以保证泥浆液面保持稳定;成槽过程中对上部土层和下部岩层深度范围内的泥浆分别间隔1.0 h和2.0 h取样测试其性能指标变化。同时,在试验过程中跟踪监测泥浆液面位置的动态变化,采用超声波检测仪对槽壁稳定状态进行跟踪监测,并详细记录试验现象和监测数据。
1.3 测试结果与分析
图2为地连墙成槽试验中泥浆参数随时间变化特征。由图2可知,随着成槽深度的增加,槽内泥浆含砂量先稍有增加而后逐渐趋于稳定,其值约为5.5%,泥浆黏度和比重基本保持稳定状态;当槽壁出现局部失稳后,槽内泥浆液面持续下降,在46 h和62 h时分别向槽内回灌泥浆,但泥浆液面仍继续下降,其下降速率呈先增大而后逐渐减小趋势,泥浆液面累计下降量为2.1 m;在槽壁失稳过程中,槽内泥浆黏度出现小幅波动,但泥浆黏度和比重未出现明显变化。现场观测表明,在成槽试验深度21.5 m范围内,槽壁未出现滑塌现象,泥浆液面基本保持平衡;当成槽试验深度超过21.5 m后发现槽内泥浆液面开始出现较大波动(初始泥浆液面位于导墙顶面下0.5 m),在导墙下槽壁出现局部滑塌,且局部滑塌区域随泥浆液面下降逐渐扩大;通过对失稳槽壁取土样发现,在槽壁已形成的泥膜厚度约为2.0~3.0 mm,见图3。

(a) 成槽泥浆深度;(b) 泥浆液面变化;(c) 泥浆性能参数
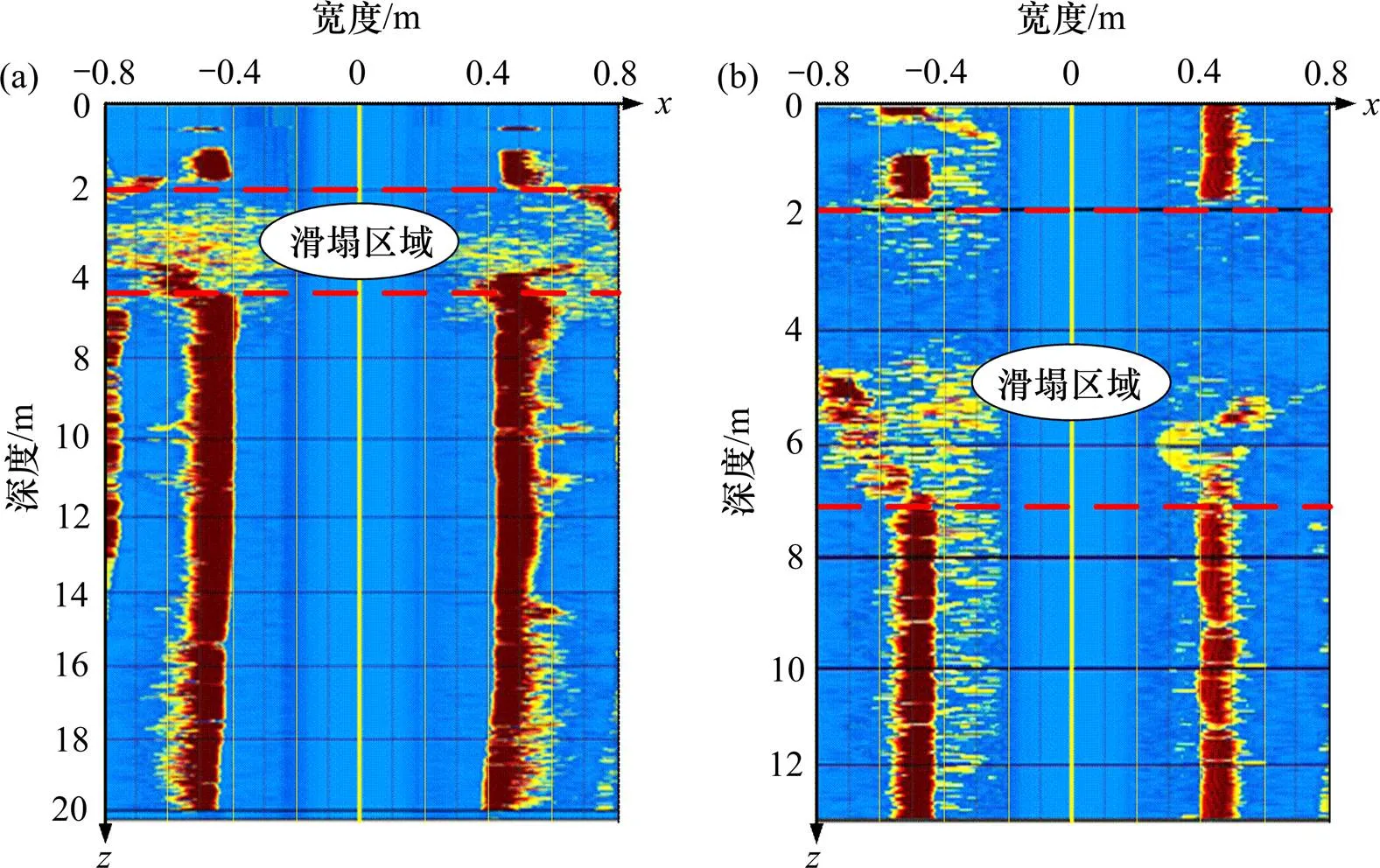
图4为成槽试验段槽壁稳定超声波现场实测结果。由图4可知,当槽内泥浆液面发生波动后,槽壁超声波检测结果表明,在导墙顶面下2.0~5.0 m范围的粉质黏土和粉土层出现局部滑塌,即表现为浅层失稳现象,见图4(a);当槽壁出现局部滑塌48 h后,槽内滑塌范围扩大至导墙顶面下2.0~7.5 m范围的粉质黏土、粉土和细砂层,在槽壁外侧形成长5.0 m×宽1.5 m×深5.0 m的凹槽,见图4(b)。槽壁发生滑塌的主要原因有:滑塌范围内的土体稳定性较差,且各土层分界面处为薄弱带,易受施工振动、泥浆参数和地下水位变化等因素影响;地连墙深度范围内存在深厚砂性土层,易造成泥浆流失和影响泥膜形成质量,且基坑三面紧邻江河,地下水位易受临近江河、降雨环境等因素影响发生较大波动,对地连墙槽壁稳定极为不利;槽内泥浆液面出现大幅波动和槽壁滑塌后,暂停成槽试验且未对槽壁采取任何加固措施,导致滑塌范围继续发展。因此,建议在地连墙成槽施工过程中严格控制泥浆参数,跟踪监测地下水位变化,并对槽壁两侧采用水泥土搅拌桩墙等措施进行预加固处理。

(a) 泥浆液面下降;(b) 槽壁局部滑塌;(c) 槽壁泥膜厚度
(a) 测试1;(b) 测试2
2 数值模拟
2.1 计算模型及材料参数
结合上述地连墙成槽试验段实际,槽宽0.8 m,深度30.0 m。根据场地岩土勘察报告,将槽段深度范围简化为黏性土、砂性土和风化泥质粉砂岩3类均匀分布的土层,各土层计算参数取加权平均值,见表1。采用有限元软件PLAXIS2D建立地连墙成槽施工渗流与变形数值模型进行槽壁稳定性特征对比分析。考虑地层的无限性及施工扰动影响范围,以地连墙横断面方向为轴,左右边界距地连墙中心30.0 m,侧面位移边界限制水平移动;以地连墙深度方向为轴,上边界为地表,下边界取36.0 m,地表为自由边界,底部固定边界限制水平移动和垂直移动。考虑模型的对称性后取1/2模型进行计算,建立的数值计算模型尺寸宽()×高()为30.0 m×36.0 m,模型共划分1 717个单元,14 067个节点,如图5所示。
在数值模拟计算中,施工场地地表铺设20 cm厚C25钢筋砼结构层,地面超载取40.0 kPa,地下水位位于地表下4.5 m。地连墙槽内初始泥浆液面位于导墙顶面下0.5 m,泥浆重度取12.0 kN/m3,成槽后即在槽壁施加线性分布荷载模拟静水泥浆压力。岩土体材料按均质弹塑性考虑,采用能较好描述土体破坏应力状态的莫尔−库仑屈服准则[15](见式(1)),利用增量理论计算;导墙、场地混凝土结构层采用线弹性模型,其计算参数见详见表1。

式中:;c为黏聚力;φ为内摩擦角。

表1 各材料主要物理力学参数
2.2 计算结果对比与分析
图6为考虑渗流作用下地连墙成槽施工土体变形分布曲线。由图可知,随着成槽深度增加,槽壁土体逐渐向槽段内移动,槽壁水平变形敏感区域主要发生在2.0~12.0 m,最大值约为−29.35 mm,其位置距导墙顶面下5.5 m;在18.5~30.0 m深度范围内(风化泥质粉砂岩层)槽壁土体向槽段外发生微小水平移动,其值约为−3.0 mm,见图6(a)。主要原因为槽段深度范围内上部为松软黏土和砂土层,下部为风化泥质粉砂岩层,且槽壁泥浆压力略小于侧向土压力,即槽壁水平变形随深度呈现上大下小的非对称“鼓肚”形曲线分布。地表竖向变形随成槽深度增加表现为沉降,沿横向水平距离呈“勺子”形曲线分布,沉降槽宽度约为(1.0~1.5)e(e为成槽深度),最大值约为−28.90 mm,其位置距槽壁水平距离约为(0.10~0.15)e;根据地表竖向变形曲线分布特征,沉降槽影响区域可分为显著影响区、过渡影响区和轻微影响区,即距槽壁水平距离(0.2~0.4)e范围为显著影响区,(0.4~0.8)e范围为过渡影响区,超过0.8e范围为轻微影响区,见图6(b)。

(a) 槽壁水平变形;(b) 地表竖向变形
考虑地连墙成槽试验深度e=−21.5 m时泥浆渗漏导致槽壁局部失稳情况,取变化后的泥浆液面H=−2.5 m。地连墙槽壁两侧采用Φ850 mm@600 mm三轴水泥土搅拌桩加固(深度20.0 m),加固桩体与地连墙间距取L=0.1 m,数值模拟计算中将槽壁加固桩等效为厚度D=0.60 m的均匀墙体。设置4种工况(工况1:不考虑渗流,槽壁未加固;工况2:考虑渗流,槽壁未加固;工况3:考虑渗流,槽壁加固;工况4:考虑渗流,槽壁未加固,泥浆渗漏H=−2.5 m)进行数值计算分析,各工况其他条件相同,则不同工况下地连墙成槽施工扰动变形对比如图7和图8所示。由图可知,工况1与工况2相比,考虑渗流作用的地连墙成槽施工扰动变形较不考虑渗流作用的大;工况2与工况3相比,地连墙槽壁土体采取加固措施后成槽施工扰动影响显著减小;工况2与工况4相比,泥浆液面下降诱发槽壁水平变形急剧增加,其变形核心区域为2.0~9.0 m,见图7。4种工况对应的最大槽壁水平变形分别为−26.93,−29.18,−23.78和−96.69 mm,以工况2水平变形值为参照,工况1,3,4分别为工况2的0.92,0.81和3.31倍;4种工况对应的最大地表竖向变形分别为−26.05,−28.17,−22.67和−121.84 mm,以工况2竖向变形值为参照,工况1,3和4分别为工况2的0.92,0.80和4.33倍,见图8。上述表明,富水砂层的不稳定性引起泥浆液面下降,进而诱发槽壁和地表产生过大变形,导致槽壁发生失稳破坏,此结果与现场试验结果(见图4)相一致,这也是成槽试验中槽壁失稳的重要原因之一。同时,采取槽壁加固措施可有效降低槽壁水平变形和地表竖向变形,对控制槽壁稳定具有积极意义。

(a) 工况1(Ux,max=26.93 mm);(b) 工况2(Ux,max=29.18 mm);(c) 工况3(Ux,max=23.78 mm);(d) 工况4(Ux,max=96.69 mm)
3 影响因素
控制槽壁稳定是地连墙顺利成槽施工的关键。基于建立的地连墙成槽施工渗流与变形数值计算模型,考虑泥浆槽壁土体加固作用,进一步分析砂土类型、地下水位、泥浆参数及槽壁加固参数变化对地连墙槽壁稳定性的影响特征,为控制地连墙槽壁稳定和施工参数优化提供参考。

(a) 槽壁水平变形;(b) 地表竖向变形
3.1 砂土类型变化
考虑不同砂土性质对成槽施工变形的影响,分别取粉砂、细砂、中砂和粗砂4种典型砂层进行数值计算,其参数变化对地连墙成槽施工土体变形分布的影响如图9所示。由图可知,各工况对应的最大槽壁水平变形U,max分别为−24.50,−34.25,−27.32,−25.35和−22.94 mm,以工况1水平变形值为参照,其他4种工况分别为工况1的1.40,1.12,1.03和0.94倍;各工况对应的最大地表竖向变形U,max分别为−23.50,−33.66,−28.92,−26.17和−21.85 mm,以工况1竖向变形值为参照,其他4种工况分别为工况1的1.43,1.23,1.11和0.93倍。可见,地层土质条件对地连墙成槽施工扰动变形影响显著。

(a) 槽壁水平变形;(b) 地表竖向变形
3.2 地下水位变化
地下水位位置分别取距地表下3.0,4.5和6.0 m 3种工况进行数值计算,其参数变化对地连墙成槽施工土体变形分布的影响如图10所示。由图10可知,3种工况对应的最大槽壁水平变形U,max分别为−31.36,−24.50和−21.67 mm,以工况2水平变形值为参照,工况1增加了28.0%,工况3减少了11.6%;3种工况对应的最大地表竖向变形U,max分别为−31.71,−23.50和−18.56 mm,以工况2竖向变形值为参照,工况1增加了34.9%,工况3减少了21.0%。可见,地下水位越高,槽壁水平变形和地表竖向变形越大,故在地连墙成槽施工过程中应重视地下水位变化对槽壁稳定的影响。
3.3 泥浆液面变化
泥浆液面变化对地连墙成槽施工土体变形分布的影响如图11所示。由图11可知,泥浆液面变化对槽壁水平变形和地表竖向变形影响显著;3种工况对应的最大槽壁水平变形U,max分别为−24.50,−29.46和−35.73 mm,以工况1水平变形值为参照,工况2和3分别增加了20.2%和45.8%;3种工况对应的最大地表竖向变形U,max分别为−23.50,−29.22和−36.22 mm,以工况1竖向变形值为参照,工况2和3分别增加了24.3%和54.1%。可见,槽内泥浆液面下降会引起槽壁水平变形和地表竖向变形增大,且地表竖向变形值的增幅高于槽壁水平变形。

(a) 槽壁水平变形;(b) 地表竖向变形

(a) 槽壁水平变形;(b) 地表竖向变形
3.4 槽壁加固间距
槽壁加固间距变化对地连墙成槽施工土体变形分布的影响如图12所示。由图12可知,5种工况对应的最大槽壁水平变形U,max依次为−24.50,−23.05,−21.89,−22.12和−24.38 mm,当槽壁加固间距超过4.0 m时,最大槽壁水平变形值开始增加;5种工况对应的最大地表竖向变形U,max依次为−23.50,−22.80,−20.88,−21.99和−25.65 mm,当槽壁加固间距超过3.0 m时,最大地表竖向变形值开始增加。以工况1为参照,定义无量纲参数=U,max(各工况对应的最大变形值)/1,max(工况1对应的最大变形值),即无量纲参数与槽壁加固间距p的关系见图13。可见,随着槽壁加固体与槽壁间距的增加,槽壁水平变形和地表竖向变形呈先减小后增大的趋势;以变形为控制目标,槽壁加固间距最优区域为[2.0,4.0] m,即为地表沉降槽最大值对应的横向水平距离位置附近。

(a) 槽壁水平变形;(b) 地表竖向变形

图13 无量纲参数M与槽壁加固间距Lp的关系曲线
4 结论
1) 深厚富水砂层地连墙成槽施工槽壁主要表现为浅层失稳,失稳区域主要发生在导墙顶面下2.0~7.5 m范围的粉土层和砂性土层,其失稳演变过程为“泥浆液面下降—槽壁局部滑塌—泥浆液面持续下降—槽壁滑塌区域扩展”;为降低成槽施工风险和确保槽壁稳定,建议对砂性土层深度范围内的地连墙槽壁两侧土体采用水泥土搅拌桩墙或高压旋喷桩进行预加固处理。
2) 槽壁水平变形沿深度方向呈现上大下小的非对称“鼓肚”形曲线分布,最大值约为−29.35 mm,其位置距导墙顶面下5.5 m;地表竖向变形沿横向水平距离呈“勺子”形曲线分布,沉降槽宽度约为(1.0~1.5)e,最大值约为−28.90 mm,其位置距槽壁水平距离约为(0.10~0.15)e。
3) 提高泥浆液面高度、降低地下水位、合理设置槽壁加固间距均能显著减小槽壁水平变形和地表竖向变形,对控制深厚富水砂层地连墙成槽稳定具有积极作用。
[1] Poh T Y, Goh A T C, Wong I H. Ground movements associated with wall construction: Case histories[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2001, 127(12): 1061−1069.
[2] 朱宁, 周洋, 刘维, 等. 苏州粉土地层地连墙施工对地层扰动影响研究[J]. 岩土力学, 2018, 39(增1): 529−536. ZHU Ning, ZHOU Yang, LIU Wei, et al. Study of silty soil behavior disturbed for installation of diaphragm wall in Suzhou[J]. Rock and Soil Mechanics, 2018, 39(Suppl 1): 529−536.
[3] 张跃明. 富水砂层中连续墙成槽与周边建筑物相互影响数值分析[J]. 岩土工程学报, 2012, 34(增1): 182−189. ZHANG Yueming. Numerical simulation of mutual influence of surrounding buildings and diaphragm wall trench construction in water-rich sand stratum[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(Suppl 1): 182−189.
[4] Fox P J. Analytical solutions for stability of slurry trench[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2004, 130(7): 749−758.
[5] OU C Y, YANG L L. Observed performance of diaphragm wall construction[J]. Geotechnical Engineering Journal of the Seags & Agssae, 2011, 42(3): 41−49.
[6] Tsai J S, Jou L D, Hsieh H S. A full-scale stability experiment on a diaphragm wall trench[J]. Canadian Geotechnical Journal, 2000, 37(2): 379−392.
[7] ZHUO H C, YANG Y Y, ZHANG Z X, et al. Stability of long trench in soft soils by bentonite-water slurry[J]. Journal of Central South University, 2014, 9(21): 3674− 3681.
[8] Tsai J S, Chang J C. Three-dimensional stability analysis for slurry-filled trench wall in cohesionless soil[J]. Canadian Geotechnical Journal, 2011, 33(5): 798−808.
[9] DING Y C, WANG J H. Numerical modeling of ground response during diaphragm wall construction[J].Journal of Shanghai Jiaotong University (Science), 2008, 13(4): 1−6.
[10] 丁勇春, 李光辉, 程泽坤, 等. 地下连续墙成槽施工槽壁稳定机制分析[J]. 岩石力学与工程学报, 2013, 32(增1): 2704−2709. DING Yongchun, LI Guanghui, CHEN Zekun, et al. Analysis of trench face stability of diaphragm wall panel during slurry trenching[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Suppl l): 2704− 2709.
[11] HAN C Y, WANG J H, XIA X H, et al. Limit analysis for local and overall stability of a slurry trench in cohesive soil[J]. International Journal of Geomechanics, ASCE, 2015, 15(5): 1−9.
[12] 王启云, 林华明, 臧万军, 等. 深厚软弱地层地下连续墙槽壁稳定性分析[J]. 科学技术与工程, 2018, 18(35): 58−64. WANG Qiyun, LIN Huaming, ZANG Wanjun, et al. Stability analysis of trench of diaphragm wall in deep water-soaked soft stratum[J]. Science Technology and Engineering, 2018, 18(35): 58−64.
[13] 缪圆冰, 江松, 黄明, 等. 基于强度折减的泥浆护壁槽局部稳定性计算及影响因素[J]. 工程地质学报, 2018, 26(4): 874−881. MIAO Yuanbing, JIANG Song, HUANG Ming, et al. Local stability calculation and factory of slurry trench with strength reduction method[J]. Journal of Engineering Geology, 2018, 26(4): 874−881.
[14] 崔根群, 刘瑶. 基于槽壁稳定性的地下连续墙成槽施工泥浆重度计算方法[J]. 现代隧道技术, 2018, 55(1): 178−183. CUI Genqun, LIU Yao. A calculation method of slurry volume-weight during trenching construction of a diaphragm wall based on the stability of slot wall[J]. Modern Tunneling Technology, 2018, 55(1): 178−183.
[15] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004. LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2004.
Study on characteristics and influence factors of slurry trench stability of diaphragm wall in deep sandy stratum
QIU Mingming1, YANG Guolin2, SHEN Quan3, DUAN Junyi2, ZHANG Peiran2
(1. School of Architectural Engineering, Yan’an University, Yan’an 716000, China;2. School of Civil Engineering, Central South University, Changsha 410075, China;3. School of Civil Engineering, Hunan University of Technology, Zhuzhou 412007, China)
Based on the diaphragm wall construction in deep water-rich sandy stratum, the stability characteristics and influence factors of diaphragm wall trench in deep water-rich sandy stratum were studied by field test and numerical simulation. The research results show that the fluctuation of slurry level is an important reason to bring out shallow instability of diaphragm wall trench in deep water-rich sandy stratum, and that the instability area is the silty and sandy soil within the range of (2.0~7.5) m below the guide wall top. The horizontal deformation of trench face with depth displays bulging-shaped asymmetric distribution of big top and small bottom. The ground vertical deformation with horizontal distance displays spoon-shaped distribution. The horizontal distance between the position of maximum settlement and the trench face is about (0.10~0.15)e(eis excavation depth) and the width of settlement tank is about (1.0~1.5)e. The control measures such as raising slurry level, reducing underground water level and reasonable setting reinforcement spacing are proposed to ensure the stability of diaphragm wall trench in deep water-rich sandy stratum. The conclusion could be referenced for the slurry trench stability control and construction parameters optimization of diaphragm wall.
diaphragm wall; slurry trench stability; field test; numerical simulation; influence factors

TU473
A
1672 − 7029(2020)05 − 1129 − 11
10.19713/j.cnki.43−1423/u.T20190669
2019−07−25
国家自然科学基金资助项目(51778641);陕西省自然科学基础研究计划资助项目(2019JQ-834);陕西省教育厅科研计划资助项目(19JK0963);延安大学博士科研计划资助项目(YDBK2017-32);延安大学科研计划资助重点项目(YDZ2019-08)
杨果林(1963−),男,湖南桃江人,教授,博士,从事岩土工程、道路与铁道工程方面的研究;E−mail:guoling@mail.csu.edu.cn
(编辑 涂鹏)
