非线性共轭梯度反演法在铁路特长隧道勘查中的应用

2020-06-08赵虎章丹贵

铁道科学与工程学报 2020年5期

赵虎，章丹贵

赵虎1，章丹贵2

(1. 四川省公路规划勘察设计研究院有限公司，四川成都 610041；2. 中铁二院工程集团有限责任公司，四川成都 610031)

由于铁路特长隧道复杂的地质情况，在对大地电磁资料采用常规线性反演时对复杂岩性、断裂构造的识别精度及速度往往不能满足勘查要求，采用非线性共扼梯度法进行反演成像，跳出线性迭代反演局限。针对非二次极小化问题，进行直接求解，能显著减小计算工作量，提升成像速度。通过玉磨线特长隧道大金山隧道中进行实际应用，快速高效地查明了隧道多处断裂构造位置，对后期地质工作的开展起到良好的指导作用。研究结果表明：非线性共扼梯度法反演能在铁路特长隧道勘查中取得理想的效果。

音频大地电磁；非线性共轭梯度；反演；铁路特长隧道

近年来，随着我国高铁建设的持续推进，西部山区铁路长大隧道越来越多，大地电磁在隧道勘察中发挥的作用越来越重要。为了取得良好的解释效果，反演方法的选择也愈发重要。目前，大地电磁应用较广的反演技术包括Bostick变换，OCCAM (光滑约束最小二乘法反演)法等。Bostick变换算法精炼、运算快速，可以大体显示出下伏地质体的电性分布。其缺点也较为明显，多解性强，抗干扰能力弱，局限性大，通常用来宏观判断地电分布。OCCAM反演核心思想是，确保电性分布连续或光滑的情况下，得到与采集数据最接近的地电模型，最终得到需要的拟合精度。OCCAM法成像结果受初始模型影响不大，反演结果稳定，与地质情况对应程度高。缺点是必须对Jacobi矩阵进行运算，导致反演效率低，在实际使用过程中具有明显局限性，特别在特长隧道反演过程中，由于数据量巨大，OCCAM难以快速成像。共轭梯度法早在1908年就有学者提出，该方法计算效率高，自20世纪50年代开始，Hestenes和Stiefel进行不断改进，并结合统计类反演方法形成了统计加迭代的组合反演方法,消除了依赖于初始猜测的缺点，成了一种广受欢迎的反演方案[1-2]。Rodi等[3-8]在2001年共同提出非线性共轭梯度法，简称NLCG，跳出线性迭代反演局限，针对非二次极小化问题，进行直接求解，其模型序列由一系列沿着计算的搜索方向的线性搜索来确定。同时NLCG采用线性系统的迭加原理和格林函数的互易关系，利用整体计算Jacobi矩阵和一个向量的乘积，显著降低了计算量[9-12]。我国学者也在本世纪初开始应用该方法进行反演计算，2014年，赵维俊等[13]在内蒙古对NLCG反演进行了专项试验，取得了不错的效果，近年来在公路、铁路大地电磁勘探中该反演方法多有应用[14−18]。新建铁路玉磨线大金山隧道位于云南省内，隧道长度超过10 km，最大埋深约456 m，隧道穿过区域地势险峻、人迹罕见、交通不便，为玉磨线代表隧道之一。隧道穿越多种地层，附近断层众多，构造运动强烈，地质环境复杂。通过采用非线性共轭梯度反演技术对大金山隧道的高频电磁测深成像结果研究，表明此方法能对复杂铁路隧道进行快速成像，能有效识别地层岩性信息及构造情况。

1 非线性共轭梯度反演概述

1.1　基本原理

逆问题通常可以表示为：

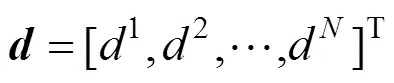
diag为对角矩阵。采集数据分为真实数据及误差。

对于大地电磁反演而言，非唯一性是其重要特性，因此适应拟合条件的模型也非唯一。为了选取最优化模型，就需要对反演进行约束，通常加入惩罚函数−模型粗糙度(roughness)条件。

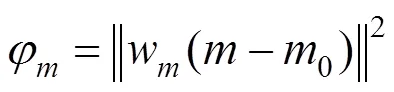
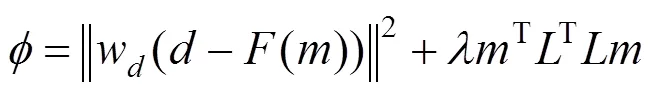
式中：为模型电阻率对数的二阶差分算子矩阵。

2.2 非线性共轭梯度反演计算步骤

1) 设立第一搜索点0，运算该处梯度值：

经过一系列计算得出：

以上所述即为非线性共轭梯度反演基本的计算步骤[19−22]。

1.3 非线性共轭梯度反演计算速度

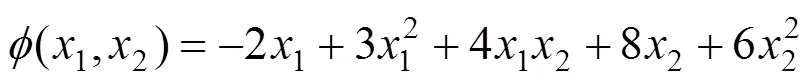
从图2可以看出，最速下降法反映目标函数的一种局部性质,从局部看，最速下降方向是目标函数值下降最快的方向，选择这样的方向进行搜索是有利的。但从全局来看，由于锯齿现象的影响, 即使向着极小点移近不太大的距离，也要经历不小的“弯路”，因此收敛速度大为减慢。而共轭梯度法则不存在锯齿现场，直接稳定的向最小值区域逼近。由此可见，在大规模的地球物理反演过程中，需要非线性共轭梯度法这样计算效率高又有较好的稳定性和可靠性的算法。

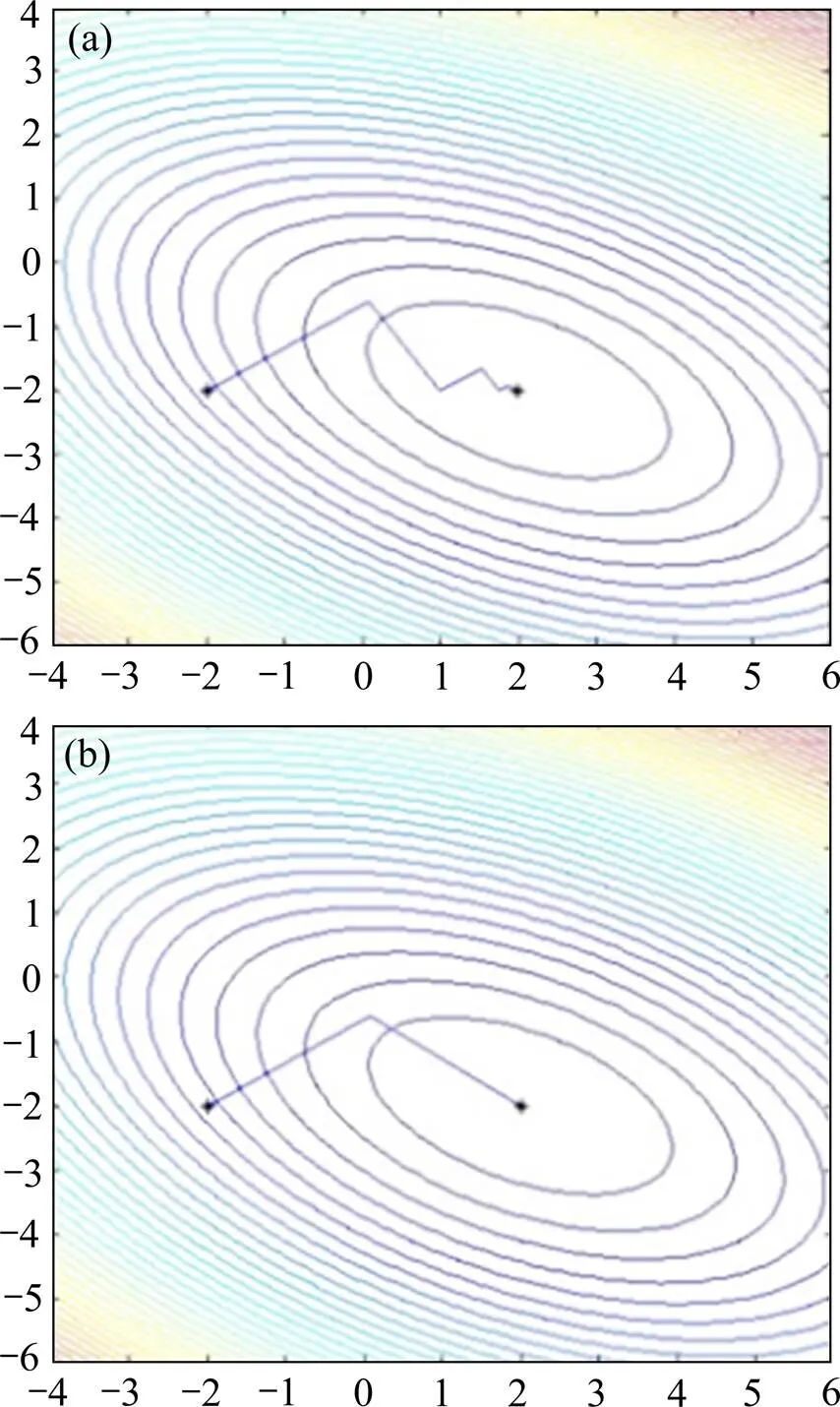
(a) 最速下降法；(b) 共轭梯度法

1.4 理论模型计算

为验证方法在隧道断层及含水区的应用效果，建立了2种简化模型，分别对应断层构造及含水区(图3和图4)，并分别对2种模型进行数值模拟，得出模拟成像结果(图5和图6)。

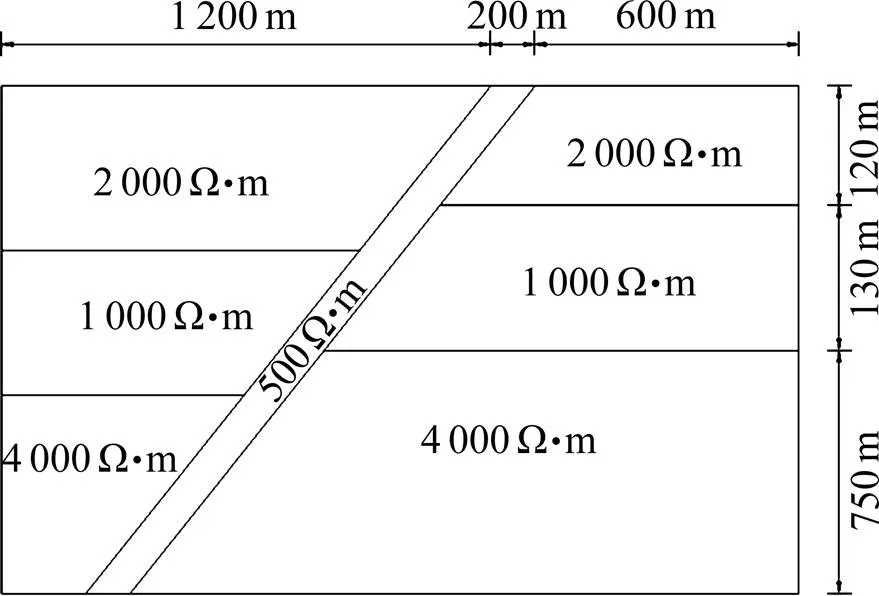
图3 断层模型

图4 含水体模型

图5 断层数值模拟结果

图6 含水区数值模拟结果

模拟结果表明，使用方法对断层及含水体均有明显反映，证明了其可行性。

2 隧道成像应用

2.1 研究区地质概况

大金山隧道为铁路典型特长隧道，总长度为10.515 km，隧道标高与实际地形最大高差接近500 m，地形起伏强烈，地势陡峭。隧道贯穿区域基岩基本被植被覆盖，露头稀少。研究对象位于欧亚板块西南方，印度板块与欧亚板块碰撞缝合带东侧，横跨扬子亚板块之康滇古隆起与滇中拗陷，印支亚板块之哀牢山褶皱带与兰坪−思茅拗陷，滇缅泰亚板块之保山褶皱带及其相互碰撞形成的缝合带，构造作用强烈。

隧道穿过区域构造较多、断层发育、岩性复杂。根据地质资料显示，共有隔界石3号断层等6条断层分布于隧道附近或直接相交，多见节理裂隙。

根据调绘及钻探资料显示，隧道通过区主要岩性有石膏、泥灰岩、泥岩和砂岩等。

研究区地表水流丰富，主要类型为沟谷流水。对洞身影响较大的地下水为基岩裂隙水及断层构造水。基岩裂隙水含量较多，断层破碎带含水量较丰富，在麻栗树断层附近发现有泉水出露，可见其断层带内可能富地下水。见图7隧道地质简图。

2.2 数据采集、处理及反演成像

在反演解释之前，沿隧道轴线进行贯通数据采集工作，为保证采集精度，采样点间隔为20 m，迭代次数选取16次迭代；采样后对反演前的数据进行处理，保证数据真实可靠性。对处理后的数据采用NLCG反演方法进行反演，得出隧道全线卡尼亚视电阻率图像如图3(小里程部分)和图4(大里程部分)。

根据成像结果分析，隧道整体电阻率值分布不均，与隧道岩性分布多样复杂对应一致。表层5~10 m范围电阻率值整体较低，对应第四纪覆盖层及强风化岩体，在断层所在位置，均反映出明显低阻条带状特征，根据前期区域内各地层的地球物理参数统计工作，结合部分典型岩石的实测电性参数，将隧道整体围岩按电阻率值划分不同类别，并根据电阻率类别预测出对应隧道围岩工程地质特征(表1)。

图7 大金山隧道地质简图

图8 大金山隧道小里程段反演成像图

图9 大金山隧道大里程段反演成像图

2.3 成果应用

反演成像结果对隧道全线地质情况及断层破碎带有较好的反映，具体成果如下。

2.3.1 洞身岩性解译

成像结果较好地反映了隧道围岩的复杂多样性，尤其是根据电阻率特征在隧道洞身标出了K207 +340～+600等13段V类电阻率段落(表2)，预测为工程地质条件极差段，为隧道设计及下一步施工提供了指导性意见。

表1 研究区电阻率特征表

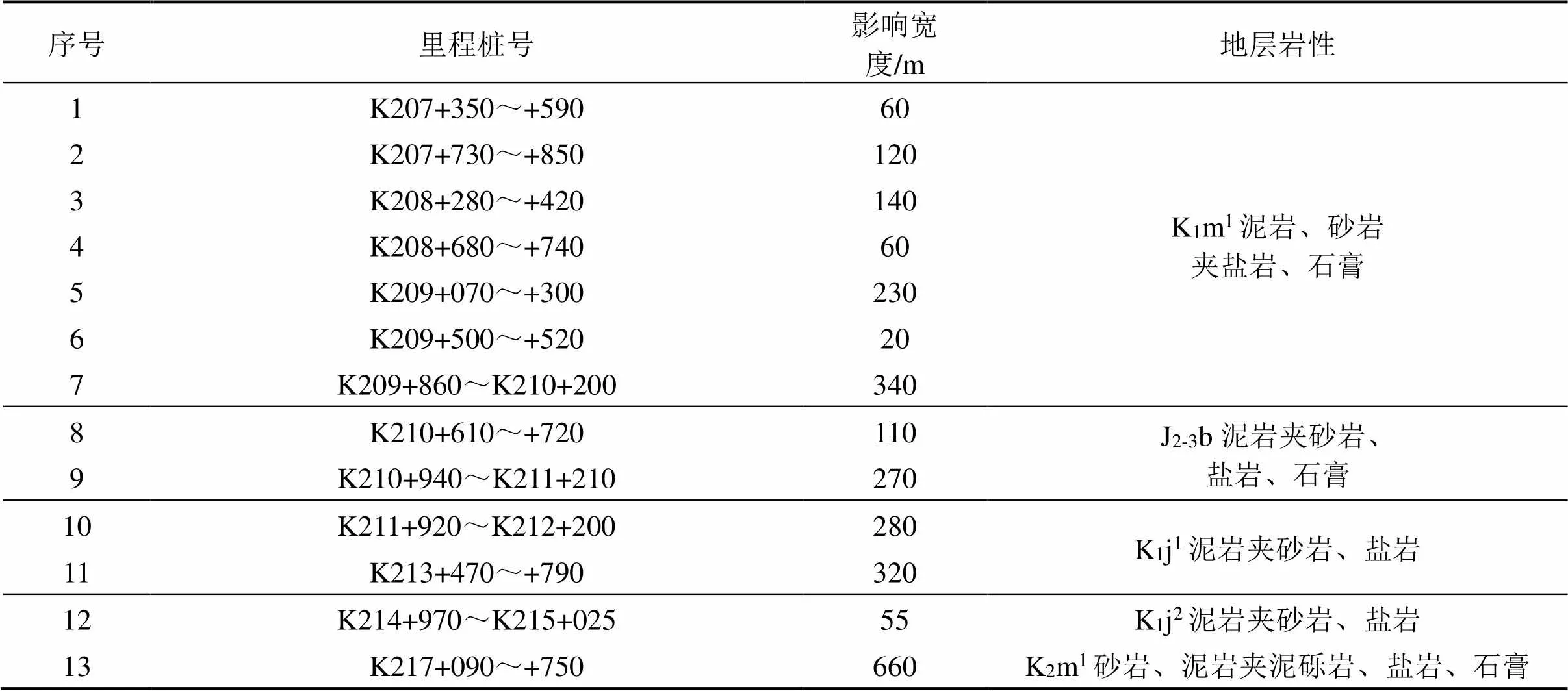
表2 大金山隧道V类电阻率异常统计表

2.3.2 地质构造解释

根据反演成像结果，将条带状低阻异常体预测为断层破碎带或背向斜构造核部，根据预测情况，共划分出8条条带状异常，经过与区域地质及现场调绘钻探验证后，确定出两异常位置为区域背斜核部，剩余6条异常带4条为区域性断裂，2条为新发现的次级断裂，分别编号为Fw1，Fw2，Fw3，Fw4，Fw5和Fw6。对断层和背斜核部电阻率特征及工程地质特征分析如表2所示。

2.3.3 地下水解译

隧道穿越地层较为复杂，既有储水地层又有隔水地层，经过对地下水赋存特征、水力特征分析，隧道穿越岩层地下水类别主要为基岩裂隙水及断层构造水。根据隧道电阻率特征，结合隧道地质条件，可初步将高阻背景岩性的低阻区域判断含水区，预测主要富水区为断层破碎带及背向斜核部区域，根据反演成像结果推测，预测的断层带、背向斜核部区域为较含水区域，施工开挖时易出现突水现象。

2.3.4 成果验证

根据物探结果，对物探成果中推测的断层及含水区域进行补充地质调绘，验证了已有断层的位置及影响带，并根据物探成果对性质不明的断裂的地质信息进行了补充和完善，成果新发现的Fw2及Fw5有效补充了现有地质资料，目前隧道正在进行施工开挖，暂无较大规模变更，较好地验证了物探成果的准确性。

表3 大金山隧道线路断层或构造破碎带统计表

3 结论

1) 通过对NLCG反演进行理论分析、算例分析，说明NLCG反演算法是一种计算效率高又有较好稳定性和可靠性的算法，适用于大规模地球物理快速成像计算。

2) 将NLCG算法对复杂特长铁路隧道进行反演成像，较好地反映了隧道岩性特征、断层、背向斜构造等不良地质。说明该反演方法在实际工作中有较好的应用价值，值得进行推广。

3) 由于大地电磁反演方法种类繁多，每种反演方法均有其可取之处及局限性，实际工作当中应根据地质情况，提前建立合适的地质模型，选取适合的反演方法，才能更好地预测地质情况。

[1] Stiefel E L. Some methods of calculating relationships[J]. Journal of Applied Mathematics and Physics, 1952, 3: 1−33.

[2] Hestenes M R. Iterative method for solving linear equations[J]. Journal of Optimization Theory and Applications, 1973(1): 322−334.

[3] Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 1(1): 174−187.

[4] LIN C H, TAN H D, TONG T. Three-dimensional conjugate gradient inversion of magnetotelluric sounding data[J]. Applied Geophysics, 2008, 5(4): 314−321.

[5] Ward S H, O’Donnell J, Rivera R, et al AFMAG- application and limitation[J]. Geophysics, 1966, 31(3): 576−605.

[6] Labson V F, Becker A, Morrison H F, et al. Geophysical exploration with audio frequency natural magnetic fields[J]. Geophysics, 1985, 50(4): 656−664.

[7] 周汝峰, 王绪本, 秦策, 等. 大地电磁NLCG与OCCAM二维反演的综合利用[J]. 地球物理学进展, 2016, 31(5): 2306−2312.ZHOU Rufeng, WANG Xuben, QIN Ce, et al. Comprehensive utilization of NLCG and OCCAM in two-dimensional magnetotelluric inversion[J]. Progress in Geophysics, 2016, 31(5): 2306−2312.

[8] 许智博, 谭捍东. ZTEM 二维非线性共轭梯度反演研究[J]. 物探与化探, 2019, 43(2): 393−400.XU Zhibo, TAN Handong. Two－dimensional nonlinear conjugate gradient inversion of ZTEM[J]. Geophysical and Geochemical Exploration, 2019, 43(2): 393−400.

[9] 夏时斌, 王绪本, 闵刚, 等. 青藏高原东北缘祁连山造山带至阿拉善地块壳幔电性结构研究[J]. 地球物理学报, 2019, 62(3): 950−966. XIA Shibin, WANG Xuben, MIN Gang, et al. Crust and uppermost mantle electrical structure beneath Qilianshan orogenic belt and Alxa block in northeastern margin of the Tibetan Plateau[J]. Chinese Journal of Geophysics, 2019, 62(3): 950−966.

[10] 徐志敏, 辛会翠, 谭新平, 等. 强电磁干扰区大地电磁远参考技术试验效果分析[J]. 物探与化探, 2018, 42(3): 560−568.XU Zhimin, XIN Huicui, TAN Xinping, et al. An analysis of the experimental result of MT remote reference technique in strong electromagnetic interference region[J]. Geophysical and Geochemical Exploration, 2018, 42(3): 560−568.

[11] 余年, 李坚, 王绪本. 二维大地电磁反演及其在铁路长大隧道勘探中的应用研究[J]. 工程地球物理学报, 2009, 6(5): 598−602.YU Nian, LI Jian, WANG Xuben. 2D magnetotellu-ric inversion and its application in the exploration of the large railway tunnel[J]. Chinese Journal of Engineering Geophysics, 2009, 6(5): 598−602.

[12] 李坚, 邓宏科, 张家德, 等. 可控源音频大地电磁勘探在大瑞铁路高黎贡山隧道地质选线中的应用[J]. 水文地质工程地质, 2009, 36(2): 72−76. LI Jian, DENG Hongke, ZHANG Jiade, et al. Application of geological routing about CSAMT exploration in Gaoligong mountain tunnel of Dali-Ruili railway[J]. Hydrogeology and Engineering Geology, 2009, 36(2): 72−76.

[13] 赵维俊, 颜廷杰, 高智超. 大地电磁非线性共轭梯度反演试验—以内蒙古扎鲁特盆地数据为例[J]. 地球物理学进展, 2014, 29(5): 2128−2135. ZHAO Weijun, YAN Tingjie, GAO Zhichao. Magnetotelluric nonlinear conjugate gradient inversion experiments: An example from data acquired in the Jarud Basin, Inner Mongolia[J]. Progress in Geophysics, 2014, 29(5): 2128−2135.

[14] 赵虎, 王玲辉, 李瑞, 等. 大地电磁测深法在高原特长隧道勘查中应用研究[J]. 地球物理学进展, 2014, 29(5): 2472−2478. ZHAO Hu, WANG Linghui, LI Rui, et al. Application of geophysical prospecting technology in survey of deeply-buried long tunnels on the plateau[J]. Progress in Geophysics, 2014, 29(5): 2472−2478.

[15] 化希瑞, 汤井田, 朱正国, 等. EH_4系统的数据二次处理技术及应用[J]. 地球物理学进展, 2008, 23(4): 1261 −1268. HUA Xirui, TANG Jingtian, ZHU Zhengguo, et al. The improvement and applications of EH-4 system data processing technique[J]. Progress in Geophysics, 2008, 23(4): 1261−1268.

[16] 曹辉, 何兰芳, 何展翔, 等. 高频电磁测深在地下热水勘探中的应用[J]. 应用地球物理(英文版), 2006, 3(4): 248−254.CAO Hui, HE Lanfang, HE Zhanxiang, et al. The application of the high-frequency electromagnetic sounding method in the exploration of underground thermal water[J]. Applied Geophysics, 2006, 3(4): 248− 254.

[17] 王辉, 叶高峰, 魏文博, 等. 大地电磁测深中大地电场的高精度采集技术[J]. 地球物理学进展, 2013, 28(3): 1199−1207. WANG Hui, YE Gaofeng, WEI Wenbo, et al. High- precision acquisition technology of telluric field on magnetotellurics[J]. Progress in Geophysics, 2013, 28(3): 1199−1207.

[18] 赵虎, 王玲辉, 李瑞. 综合电法在深埋长隧道勘查中的应用研究[J]. 勘察科学技术, 2008, 2(2): 61−64. ZHAO Hu, WANG Linghui, LI Rui. Application study of synthetic electrical prospecting for deep-buried long tunnel exploration[J]. Site Investigation Science and Technology, 2008, 2(2): 61−64.

[19] Louis Cagniard. Basic theory of the magnetotelluricmethod of geophysical prospecting[J]. Geophysics, 1953, 18(3): 605−635.

[20] K·Vozoff. The magnetotelluric method in the exploration of sedimentary basins[J]. Geophysics, 1972, 37(1): 98− 141.

[21] 梁宏达. 大地电磁反演方法对比研究[J]. 工程地球物理学报, 2012, 9(5): 537−543.LIANG Hongda. Comparison among several inversion algorithms of MT[J]. Chinese Journal of Engineering Geophysics, 2012, 9(5): 537−543.

[22] 陈理, 秦其明, 王楠, 等. 大地电磁测深正演和反演研究综述[J]. 北京大学学报(自然科学版), 2014, 50(5): 979−984.CHEN Li, QIN Qiming, WANG Nan, et al. Review of the forward modeling and inversion in magnetotelluric sounding field[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(5): 979−984.

Application of NLGC inversion method in exploration of extra long railway tunnels

ZHAO Hu1, ZHANG Dangui2

(1. Sichuan Highway Planning, Survey, Design and Research Institute Ltd, Chengdu 610041, China; 2. China Railway Eryuan Engineering Group Co., Ltd (CREEC), Chengdu 610031, China)

Because of the complex geological conditions of railway extra-long tunnels, the accuracy and speed of identifying complex lithology and fracture structures in conventional linear inversion of magnetotelluric data can not always meet the requirements of investigation. In this paper, the nonlinear conjugate gradient method was used for inversion imaging, which overcame the limitation of linear iterative inversion. For the non-quadratic minimization problem, the direct solution was carried out, which significantly reduced the computational workload and improves the imaging speed. Through practical application in Dajinshan Tunnel of Yumo Line Extra-long Tunnel, the locations of many faults in the tunnel were quickly and efficiently identified, which played a good guiding role in the later geological work. The results show that the inversion of stochastic non-linear conjugate gradient method can play an ideal role in the exploration of extra-long railway tunnels.

audio-frequency magnetotelluric; nonlinear conjugate gradient; inversion; railway extra long tunnel