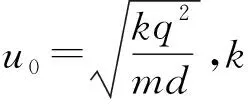有效势能在高中物理竞赛中的应用

胡少希 孙 伟

(1. 南京市玄武区教师发展中心,江苏 南京 210016; 2. 江苏省泗阳中学,江苏 泗阳 223700)

在有心力作用下质点的运动是比较常见的运动,这类问题在竞赛考题中出现的频率很高,质点的有心力问题用力心为极点的极坐标系描述较为适宜.在极坐标系中物体的机械能满足

(1)

有心力作用下质点角动量守恒

L=mrvθ.

(2)

联立(1)、(2)式得

(3)

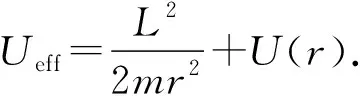
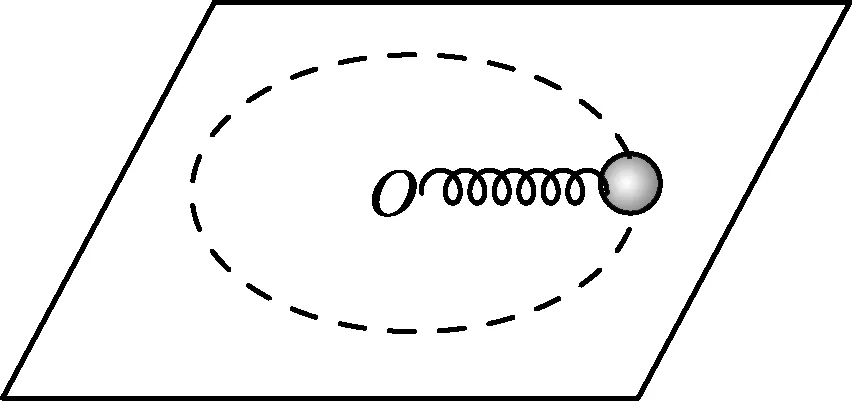
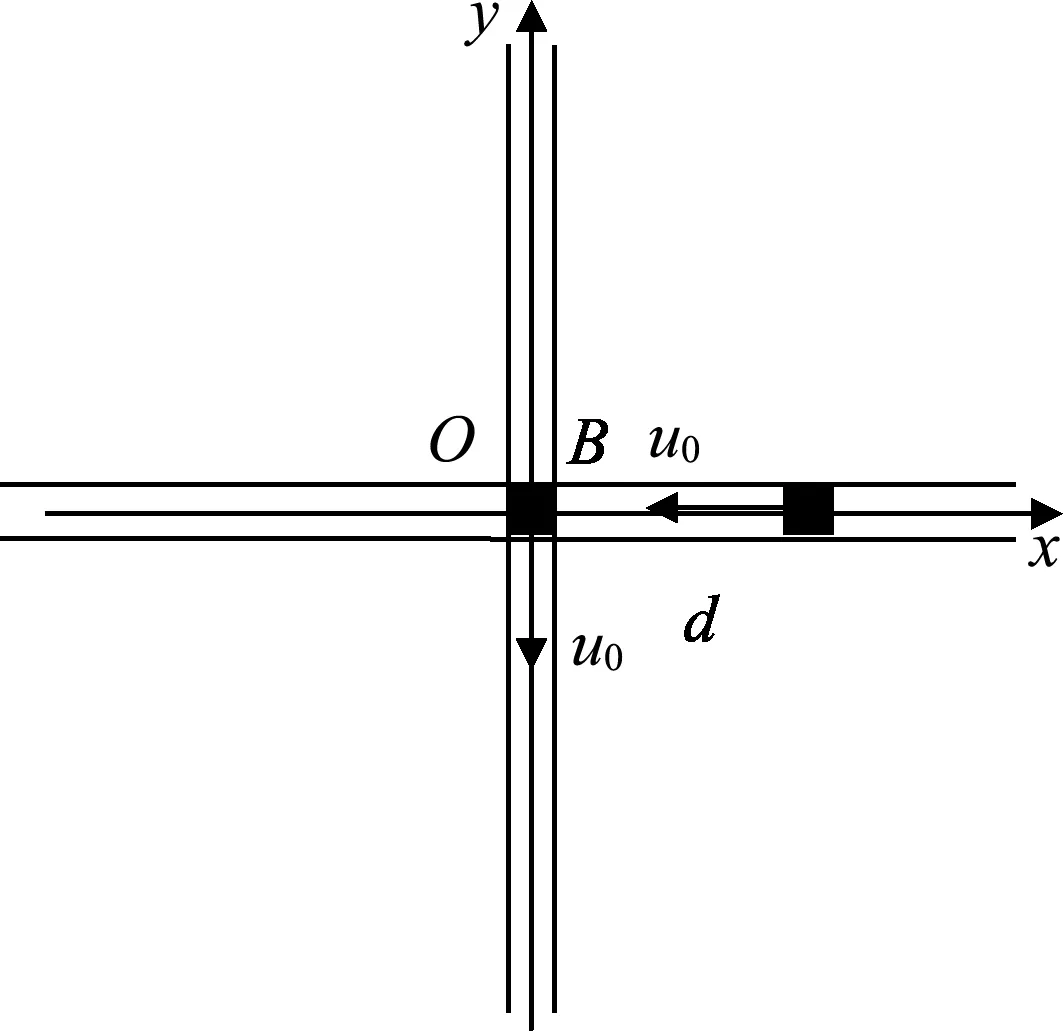
图1

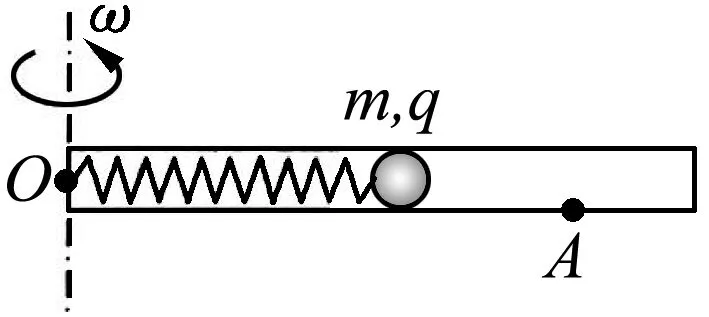
例1.(国家集训队)如图1所示,在光滑的水平面上,一个劲度系数为k=3.0 N/m的轻弹簧一端固定于O点,另一端拴接一个质量为m=2.0 kg的小球,假设弹簧在无力作用时没有原长.若小球在弹簧作用下作匀速圆周运动,系统总机械能为E=12 J,现沿小球运动的径向给其突如打击,使小球瞬间获得一径向速度vr0=1 m/s,求此后运动过程中小球距O点的最近距离和最远距离.

解析:设小球受打击前运动的速度为v0,轨道半径为r0,则

(1)

(2)

联立(1)、(2)式得

(3)

小球受打击后系统能量为

(4)

代入数据得

E′=13 J.

(5)

有效势能为

(6)

由于径向打击不影响小球的角动量,故小球角动量守恒,即

L=mv0r0.

(7)

联立(6)、(7)式代入数据得

(8)

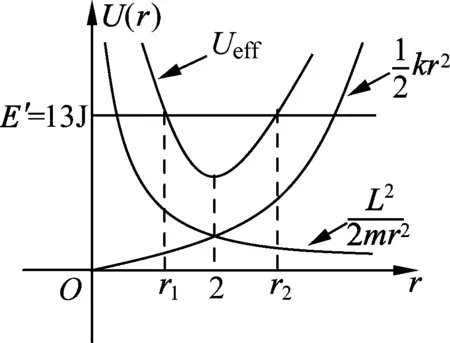
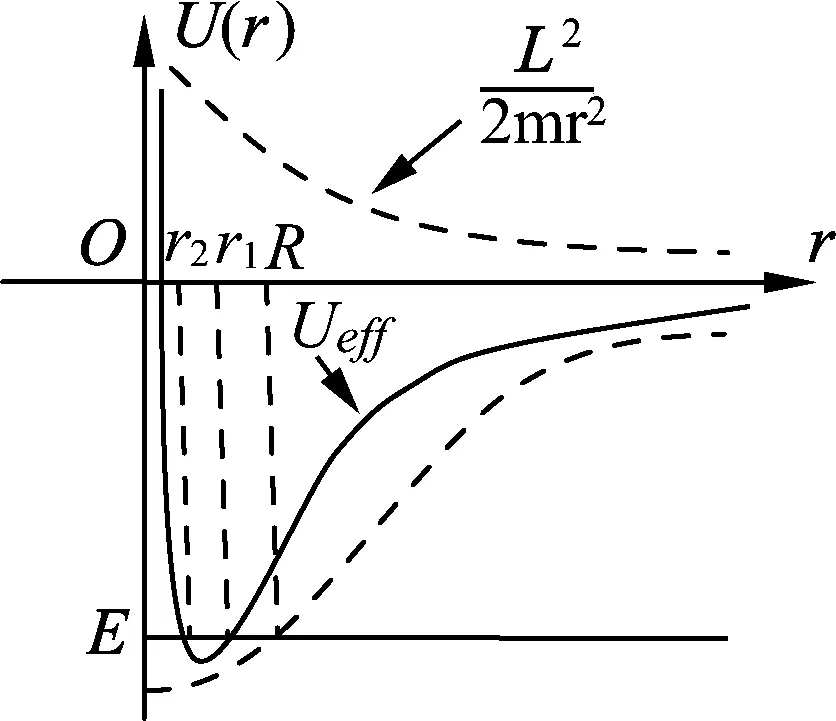
图2

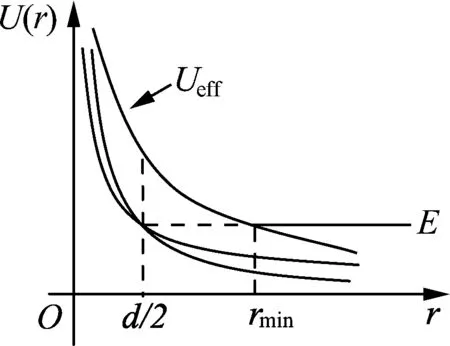
作出有效势能图线,如图2所示.小球的径向运动满足E′≥Ueff,结合图2可知小球的径向运动范围在r1与r2之间,当E′=Ueff时,联立(5)(8)式得

(9)

由(9)式得

r1=1.63 m，r2=2.45 m.

(10)

分别为小球运动过程中距O点的最近距离和最远距离.

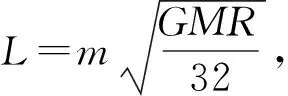
(1) 试问此子弹的运动是总在云里?总在云外?还是有时在云里,有时在云外?

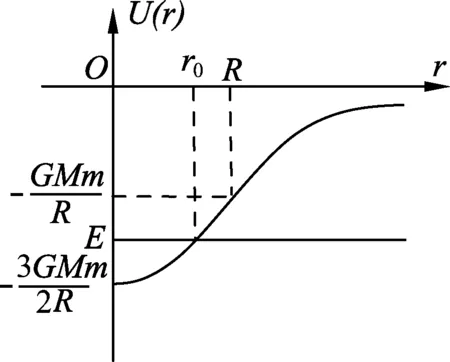
图3

(2) 求子弹运动轨道的转折点离气体云中心的距离;

(3) 讨论子弹运动轨道的形状,并求其运动周期.

解析: (1) 在r≤R区域,子弹受到气体云团的万有引力大小为

(1)

在r>R区域,子弹受到气体云团的万有引力大小为

(2)

选择无穷远为引力势能零点,则在r≤R区域,引力势能

(3)

则在r>R区域,引力势能

(4)

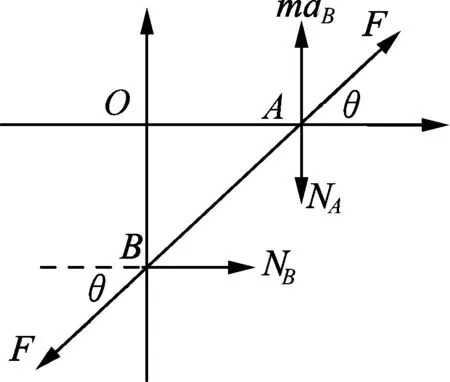
作出势能图线如图3所示,子弹能出现的区域应满足E≥U.由图3知,只有在r≤r0区域子弹才可能出现,而r0

(2) 子弹的有效势能

(5)

图4

作出有效势能图线,如图4所示.轨道转折处满足

E=Ueff.

(6)

联立(5)、(6)式得

(7)

解得

(8)

(3) 根据以上讨论可知,子弹的机械能与有效势能曲线有两个交点,因此子弹运动为椭圆轨道,其半长轴和半短轴分别为

(9)

(10)

子弹相对气体云中心角动量守恒,可知其面积速率k为恒量,其满足

(11)

故子弹轨道运动的周期

(12)

图5

解析:分析某时刻质点A和B受力知，

质点A:

Fsinθ=NA.

(1)

质点B:

Fsinθ=maB.

(2)

图6

以质点B为参考系,质点A还受到大小为maB的惯性力,如图6所示.由(1)(2)式知:此惯性力正好与弹力NA平衡.也就是说,以B为参考系,A相当于在有心力场中运动.设A、B间距离为r,则A的有效势能为

(3)

其中A相对B的角动量

(4)

把(4)式代入(3)式得

(5)

A相对B的能量

(6)

图7

画出有效势能图线如图7所示,E≥Ueff是可能的运动区域,二者距离最近时满足

E=Ueff.

(7)

图8

(1) 弹簧系数k0及小球在B处时细管的转速;

(2) 试问小球在平衡点B附近是否存在相对于细管的径向微振动?如果存在,求出该微振动的周期.

解析: (1) 设细管的角速度为ωA,小球在A点相对细管平衡时

(1)

小球在平衡B点满足

(2)

小球由A处至B处过程满足角动量守恒

(3)

联立(1)-(3)式得

(4)

(5)

(2) 在转动参考系中,小球相当于在有心力作用下运动,设小球距O点的距离为r,则其有效势能为

(6)

其中小球的角动量

(7)

对(6)式求二阶导数并把(7)式代入得

(8)

联立(4)、(5)、(8)式得

(9)

故该微振动的周期

(10)

通过以上分析,对有心力作用下物体运动引入有效势能,把二维平面运动问题转化为一维问题来处理,不失为一种解决问题的好方法.