“每日一得”作业实践初探

□徐建芳

一、梯次掉队现象

笔者对三年级到五年级学生的学习情况进行了统计，发现学生“梯次掉队”的现象十分明显，如图1、图2所示。随着年级的升高，学生学习数学所需的各种思维能力的要求也越高，当思维能力不足的时候，掉队是必然的。那么在小学阶段，如何避免这种现象产生呢？

图1 计算部分优秀率统计图

图2 应用部分优秀率统计图

二、原因探究

（一）参与教学缺动力

【教学片段1】

师：我们已经掌握了2 和5 的倍数的特征，你能来说说2的倍数有什么特征吗?

生：个位上是0，2，4，6，8的自然数是2的倍数。师：那么5的倍数有什么特征呢？

生：个位上是0或5的自然数。

师：这节课我们学习“3的倍数的特征”(板书课题)，你猜想3的倍数有什么特征？

这是一节新授课，对这几个简单问题，教师预设学生的举手率会在95%以上，但实际教学中愿意举手参与到课堂中来的学生少。在小学高年级，那些慢慢掉队的学生参与课堂的积极性弱了，虽然人在课堂，却不愿意积极思考。

（二）思维僵化缺变通

到了小学高年级，学生在数学思维或反思能力方面有了明显的差距，有的学生会举一反三，梳理总结能力强，而掉队的学生在这方面就比较弱，思维僵化缺变通，遇到拐弯的问题就没辙了。

【教学片段2】

教师出示这样一题：

生：将A设定为最小的5代入，求出A=60，然后找到60的因数有12个。

生：用有序思考罗列的方法，从小到大找到因数有1,2,3,4,A,6，12,2A,3A,4A,6A,12A,一共有12 个因数。

生：A 是一个未知量，A 如果很大，那么因数也会有很多；如果A很小，那么因数个数也会很少，所以答案是无法确定的。

找一个数的因数的方法课堂上都学过，遇到未知项可以用具体数字代入的解题方法也学过，这题只是对基础题型稍加改变，部分学生就感到手足无措了。

（三）方法单一缺构建

学生缺乏主动建构知识的方法，对整册或整个小学阶段的数学知识没有建立一个认知体系，他们在学习中的软肋是不关注题目背后知识的关联，缺乏系统性。

【教学片段3】

在长方体与正方体表面积的练习课上，教师出示了这样一道拓展题：一个棱长为15 厘米的正方体，挖去一个棱长是5 厘米的小正方体后，表面积是多少平方厘米？

学生思维的差异马上就显现出来了。有学生只想到①号的情形，并且采用逐一相加的计算方法；有学生想到①号的情形，计算时用了平移修补的方法，马上发现表面积是不变的；也有学生想到挖掉的小正方体可以有①②③三种情形，同时归纳总结能力较强，发现体积的变化和原来平面图形周长的变化有联系，可以用已有经验方法来解决问题（如图3）。

图3

学好数学，掌握方法很重要。教师要引导学生按照数学的原理去学数学，养成良好的学习与解题习惯。学生差异的形成，既有客观原因，也有主观因素。教师在教学时要关注后百分之三十学生的学习兴趣与参与度，也要关注他们的学习方法是否合理。

三、寻思良策

为改变现状，笔者决定采用“每日一得”复习本的形式，通过一课一得，在合适的年龄段助力学生的数学学习。

（一）大任务驱动：明确目标，激发兴趣

基于以上的现状分析与学习金字塔理论，笔者采用了低起点、高观点的结构性作业，即课后梳理“每日一得”，让学生在课后梳理本节新授课的知识点，激发学生学习的内驱力（如图4）。

图4

学生完成的“每日一得”也许难易有别、层次不同、形式各异，但这样的弹性作业，学生选择的空间很大。课后学生可以小组为单位互相学习，或是以班级板报展示等方式互补知识点的建构。

（二）结构可视化：利于归纳，促进思考

结构清晰的知识，容易被记住。思维导图就是一种清晰的、结构化的表现方式。很多人喜欢用思维导图，因为思维导图能使思维可视化。

（三）多元化梳理：深度学习，建构知识

学完一册数学书，可以用清晰、简洁的示意图来梳理所学知识的核心观点，使人一下子就能看到重点，比用一大段文字进行说明更有说服力。

四、实践策略

数学学习中教师应培养学生结构化思维的习惯，从整体到局部，突出重点，纵向横向分析，以形成模式，最终促进学生的深度学习。

（一）“每日一得”作业要求

1.形式多样

基于学生之间的差异，教师在设计“每日一得”作业时起点应放低，可以让学生在复习本上写一写每天的学习心得，如：我学会了什么，还有什么疑惑等。字数、形式都不限，数学小日记、表格、思维导图等均可（如图5）。这样做能有的放矢，每个学生都能发挥自己的个性，记录所思所想。

2.结构清晰

优秀的学生会将知识按层次进行排列，知识点之间有联系有结构，最后形成知识网络。在完成“每日一得”知识梳理时，教师要求学生不应只是把书本上的概念性知识点抄一遍，而应该根据教师上课梳理的重难点进行重新的编码建构，将所学知识内化到自己的知识网络中去。

3.难易有别

作业分层这一做法在面向全体学生的同时，更关注和尊重了每个学生的个体差异，让学习更有的放矢。学生在梳理当天的“每日一得”时，可以有作业量上的分层，也可以有作业难易程度上的分层（如图6）。

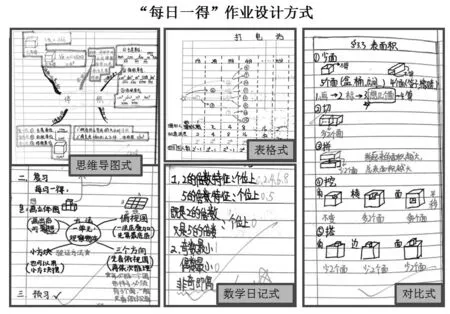
图5

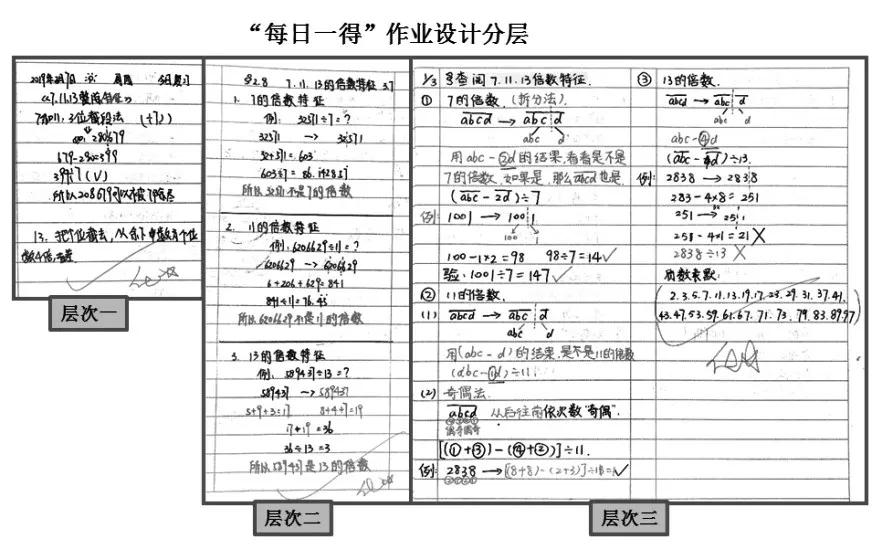
图6

例如学完“2，3，5的倍数特征”后，教师又以微课的方式组织学生学习“7，11，13的倍数特征”，这个知识点属于课外拓展内容，学习能力强的学生能够通过微课知道更多的数学知识，接受能力一般的学生也可以由此感知一部分知识，学生在当天的“每日一得”作业中只需要记录梳理自己所理解的知识即可。

（二）“每日一得”作业内容

1.连点

上完一节新授课后会有很多的概念性知识，部分学生喜欢将概念像背课文一样加以背诵记忆。经过结构化训练之后，学生会将每一课的知识点连成串，更关注知识之间的纵向关联，这样建构起来的数学概念直观易记。以下是有关倍数因数概念性问题的学生习作（如图7）。

图7

学习数学概念并建立概念模型，学生要经历自主消化、吸收的过程，在自学的过程中，学生自己领悟其中的本质，才能达到自悟的高度。

2.串线

依据由简到繁、逐一罗列、依次递增的认知顺序，学生能由此及彼找到同类型的知识，然后将它们串成一个体。

例如教材仅要求掌握2，3，5的倍数特征，学生也会思考7，11，13……倍数的特征。再如3和9的倍数有共同特征吗？这不需要全员掌握，教师可以通过微课给学生拓展知识点，有兴趣的学生会在“每日一得”中记录下这些让自己“跳一跳才能够得到”的知识，以满足他们的求知欲望。如图8 是有关数的倍数特征的学生习作。

图8

3.成面：织成连通的网络

将相似的知识点归纳起来，形成一张网。当提取一个知识点时，其他知识也会连带显现，这对数学学习有事半功倍的效果。学生通过归纳，深谙了其中的规律，可规避顾此失彼、迷茫的状态。

如“因数与倍数”单元概念较多，知识点比较零散且抽象又难记忆，为了避免眉毛胡子一把抓的情况，教师可要求学生将素材进行加工，以“数的族谱”为主线，充分调动学生学习的积极性，把零散的知识点串联起来，形成知识体系。如图9是有关数的族谱的学生习作。

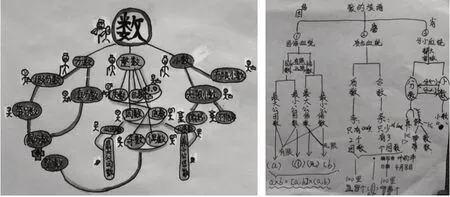
图9

4.建体

知识谱图的立体构建能反映各元素之间的各种相互关系，如因果关系、从属关系、先后关系、逻辑关系、辩证关系等，也是数学素养的重要内容。

处于中下学习水平的学生往往学了A 忘了B，对于知识点之间的因果关系、逻辑关系感到十分混乱，很难驾驭各类题型的举一反三。通过“每日一得”作业的练习，将各类元素逐一梳理，到单元结束后，就会有一种豁然开朗的大局感。如图10 是有关分数的意义与性质建体的学生习作。

“每日一得”作业让学生每天都要回想已经学过的知识，这样能巩固记忆，强化新知与已知的联系，同时能适当调整学生的学习策略，在厘清算理、透析概念、解决问题方面有了一些改变，在“简洁”“结构化”的过程中，发展了学生的思维能力。

图10