基于节点相异性指标的网络社团检测算法

刘亚东，覃 森

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

近年来，随着机器学习和深度学习的快速发展，人们能更快更好地了解复杂世界。复杂网络将现实中的实体抽象为网络中的节点，网络中的边对应于实体之间的关系。随着研究的深入，学者们发现：可以将整个网络看成由若干个社团构成，同一社团内的连边连接紧密，而不同社团之间的连边连接稀疏[1]。复杂网络中社团结构的检测对分析网络的拓扑结构和层次结构、理解社团的形成过程、发现复杂网络的内在演化规律等具有十分重要的意义；此外，社团结构检测也有重要的现实意义，如在科研合作网络中，把方向、兴趣和研究内容相关的科学家划分到同一个社团中，可以向某位科学家推荐同一社团内其他成员以促进他们之间的合作，从而推动科研的发展。

1927年，S.A.Rice[2]开始对政治网络进行社团结构的调查研究，到1995年，R.S.Weiss和E.Jacobson[3]第一次提出较为完善的社团结构检测方法，在2002年，M.E.J.Newman等[4]提出一种基于边介数的社团检测算法(Girvan-Newman，GN)，通过从网络中不断移除介数最大的边来确定网络的社团结构。GN算法的提出掀起了社团检测研究的热潮，许多领域的学者从不同角度相继提出了不同的社团检测算法，主要可以分为基于模块度优化的算法、基于传播思想的算法、基于分级聚类的算法。基于模块度优化的算法主要包括贪婪算法[5]和极值优化算法[6]等；基于传播思想的算法主要包括标签传播算法(Label Propagation Algorithm，LPA)[7]和在此基础改进的COPRA算法[8]等；基于分级聚类的算法主要包括基于邻居节点相异性的社团发现新算法[9]和基于多层节点相似度的社区发现算法[10]等。目前，网络社团检测算法仍然存在诸多问题，如节点相异性构造、相异性指标的选择、算法划分精确度低、时间复杂度高等问题。针对节点相异构造和算法精确度低，本文定义了3种相异性指标，并结合相异性指标，提出基于节点相异性指标的网络社团检测算法。

1 相异性指标定义及算法描述

1.1 相异性指标定义

(1)

图1 节点邻居集合关系的文氏图

式中，Γi-j表示节点i的邻居但不属于节点j的邻居的集合,Γi表示节点i的邻居集合，|Γi∪Γj|表示节点i和节点j所有邻居节点的个数。节点邻居集合关系如图1所示。

(2)

(3)

式中，Γij=Γi-j+Γj-i=(Γi∪Γj)-(Γi∩Γj)，k(z)表示节点z的度，a∈Γ(i)，b∈Γ(j)，k(a)+k(b)表示节点i和j的所有邻居的度之和，m表示网络的边数，2m代表网络中所有节点的度之和，节点相异性越大越可能出现在不同社团中。2-邻居相异性指标是衡量A和B互不认识对方朋友的朋友人数在A和B两层朋友中所占的比例，全局2-邻居相异性指标是衡量A和B互不认识对方朋友的朋友人数在整个朋友关系网中所占的比例。

1.2 评价指标模块度Q和标准化互信息NMI

模块度是衡量社团检测算法划分结果的一个指标，通常模块度的值越大划分出的结果越好。模块度是指网络中连接社团内部节点的边所占的比例与另外一个随机网络中连接社团内部节点的边所占比例的期望值相减得到的差值[11]，其定义如下：

(4)

式中，m表示网络的边数，aij表示网络邻接矩阵中的元素，当i和j相连时aij=1，否则为0，δ表示隶属函数，当节点i和j属于同一个社团时δij=1，否则为0。Q的取值范围为[-0.5,1.0)，在实际应用中Q的最大值一般为0.3～0.7。

标准化互信息(Normalized Mutual Information，NMI)是度量社团检测结果与真实社团结果相近程度的一个重要衡量指标[12]，其定义如下：

(5)

式中，E表示实际社团情况，F表示算法检测的社团情况，CE和CF分别表示E和F的真实社团数目，mij表示混乱矩阵M中的元素，mi·表示混乱矩阵中第i行的总和，m·j表示混乱矩阵中第j列的总和，n表示网络的节点个数，NMI的取值范围为0～1，其值越大表明划分越准确。

1.3 算法描述

把网络中连通分支个数视为社团个数，初始状态下的网络视为一个社团，基于节点相异性指标的网络社团检测算法流程如下：

(1)计算网络中有连边的节点间相异性值，找到相异性值最大的2个节点，删除两者之间的边；

(2)判断社团的个数是否增加，若有增加则计算出此时网络的模块度；

(3)重复步骤1和步骤2直到网络中所有的边都被删除；

(4)找到最大模块度对应的划分结果，即为网络的最佳社团结构。

算法开始时，计算有连边的节点间相异性值，对于有m条边的网络来说，时间复杂度为O(m)，删除相异性值最高的2节点之间的边(可能不止1条)，再计算网络中剩余所有边2节点间的相异性值，直到所有的边都被删除，所以，总的时间复杂度不会超过O(m2)。

2 实验结果与分析

2.1 计算机模拟网络与真实网络

(1)LFR基准网络[13]是目前复杂网络领域中社团检测常用的人工模拟计算机生成网络。本文采用的基准网络节点数为128，节点的平均度为16，节点的最大度为16，最大社团和最小社团包含的节点数均为32，混合参数为0.1，网络的社团个数为4。

(2)Zachary网络是测验社团检测算法最为常用的典型实际网络，由W.Zachary对美国一所大学空手道俱乐部进行2年观测后构建的，包含34个节点，78条边，每个节点代表1个俱乐部成员，边表示2个成员间有交往关系。由于某种原因，该网络分成2个小型俱乐部。

(3)Football网络由M.E.J.Newman和M.Girvan收集的美国高校足球联赛数据构建的一个真实复杂网络，包含115个节点，613条边，每个节点代表1支高校球队，节点之间的边表示2支球队至少有过1场比赛，全部的球队分为12个联盟。

2.2 社团检测过程示例

以全局2-邻居相异性指标为例来说明1个由15个节点、34条边组成的小型网络的社团检测过程。根据1.3节的算法流程计算全局2-邻居相异性指标。计算网络中34条边对应节点间相异性值，得到网络中节点8和11间的相异性值在整个网络中最大，为0.632 4，将8和11之间的边删除，此时社团的个数并未增加；计算剩余有连边的节点间相异性值，通过比较相异性值得到节3和10之间的相异性最大，为0.530 3，删除3和10之间的边，得到2个社团，分别为1,2,3,4,5,6,7,8,9和10,11,12,13,14,15，模块度为0.439 4；再计算余下有边相连节点间的相异性值，通过计算和比较得到节点2和5之间的相异性最大，为0.390 6，删除节点2和5之间的边，得到3个社团，分别为1,2,3,4和5,6,7,8,9及10,11,12,13,14,15，模块度为0.543 3；继续计算，直到网络中所有边都断开。最后，通过比较不同划分下的模块度，得到当社团数为3时的模块度最大，对应的划分结果如图2所示。

图2 计算机模拟的小型网络

2.3 实验结果分析

在LFR基准网络、Zachary网络和Football网络中，使用本文算法，得到3种指标在不同网络中的模块度随社团个数的变化情况如图3所示。图3中，指标1、指标2、指标3分别代表单层邻居相异性、2-邻居相异性和全局2-邻居相异性。

图3 3种指标在不同网络中的模块度变化情况

从图3可以看出：在LFR基准网络中，当网络被划分为4个社团时，3种相异性指标的模块度均达到最大，为0.650 4，这与LFR基准网络有4个社团的情况相符。在football网络中，当网络被划分为11个社团时，单层邻居相异性和2-邻居相异性指标的模块度值达到最大，分别为0.581 3和0.600 2；当网络被划分为12个社团时，全局2-邻居相异性指标的模块度值达到最大，为0.582 1，虽然说使用2-邻居相异性指标得到的最大模块度在3个指标中的值最大，但Football网络的真实情况是12个社团，所以说三者中全局2-邻居相异性指标更符合真实情况。在Zachary网络中，当网络被划分15个社团时，单层邻居相异性指标的模块度值达到最大，这与Zachary网络2个社团的真实情况相差较大；当网络被划分为5个社团时，2-邻居相异性指标的模块度值达到最大，为0.349 0，当网络被划分为2个社团时模块度值接近于0；对于全局2-邻居相异性指标，当网络被划分为2个社团时模块度为0.371 8。从3个相异性指标在模拟网络和真实网络划分的社团情况来看，采用全局2-邻居相异性指标检测出的社团个数与真实情况吻合度最高，所以，下面实验结果中，无特殊说明，得到的结果是均采用全局2-邻居相异性指标。

将本文算法应用到LFR基准网络中，网络被划分为4个社团，具体划分情况如图4所示。

图4 LFR基准网络社团结构图

将本文算法应用到Zachary网络中，网络被划分为2个社团，与真实情况对比发现：只有节点10被错误划分，具体划分情况如图5所示。

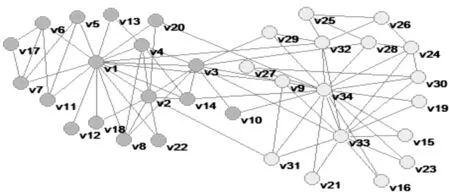
图5 Zachary网络社团结构图

将本文算法应用到Football网络中，网络被划分为12个社团，具体划分情况如图6所示。

图6 Football网络社团结构图

社团划分的准确程度采用的评价指标是标准化互信息NMI，本文算法与GN算法、FastNewman算法在LFR基准网络、Zachary网络和Football网络中划分结果的NMI值如表1所示。

表1 不同算法划分的NMI值比较

从表1可以看出：在LFR基准网络中，3种算法的NMI值均为1.000，说明划分结果与真实的社团情况一致；在Football网络中，本文算法的NMI值高于GN算法和FastNewman算法，在Zachary网络中，本文算法的NMI值高于FastNewman算法。综上，本文算法的划分准确度更高一些。

3 结束语

本文定义了3种相异性指标：单层邻居相异性、2-邻居相异性和全局2-邻居相异性，并结合这3种相异性提出了基于节点相异性指标的网络社团检测算法，通过实验对比发现采用全局2-邻居相异性指标的划分结果最好，本文算法的准确度优于GN算法和Fast Newman算法。但是，本文实验中所选用的都是非重叠社团结构网络，后续研究将尝试把本文算法应用到重叠社团网络中。