非线性模糊Volterra积分微分方程的解析解
2020-06-08马逸民洪世煌
马逸民,洪世煌
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
模糊Volterra积分微分方程是模糊分析理论的重要组成部分,在控制理论中具有重要的理论意义和应用价值。许多学者对模糊Volterra积分微分方程做了大量研究。如B.Bede等[1-2]给出广义Hukuhara导数的概念,利用特征定理将一阶模糊微分方程转化为微分方程组,求出一阶模糊微分方程的数值解。J.Matkowski[3]研究了度量空间上的广义压缩。本文主要讨论非线性模糊Volterra积分微分方程的解析解,证明了非线性模糊Volterra积分微分方程解的存在唯一性,推广了文献[2]中的特征定理,并获得了非线性模糊Volterra积分微分方程的解的解析表达式。
1 预备知识
R表示实数集,记RF={u|u∶R→[0,1]},若下列性质成立,则称RF为模糊数空间[1-2]。
(1)u是正规的,即存在x0∈R,使得u(x0)=1;

(3)u在R上是上半连续的;
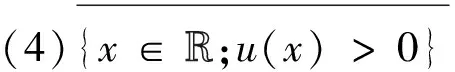
显然R∈RF,其中R={X{x}∶x是一个常实数},X是一个特征函数。

定义函数d∞∶RF×RF→R+∪{0}如下:对于任意的u,v∈RF,
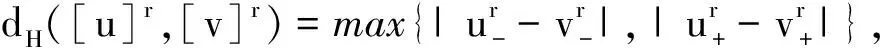
定理1[3]令(X,d)是完备度量空间,自映射T∶X→X满足

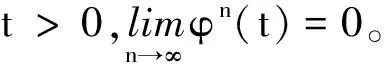
定义1[2,4]令x,y∈RF。若存在z∈RF,使得x=y+z,则称z是x与y的Hukuhara差,记作x-Hy。
定义2[1]令f∶(a,b)→RF且x0∈(a,b)。若存在f′(x)∈RF使得:
(1)对于足够小的h>0,f(x0+h)-Hf(x0)和f(x0)-Hf(x0-h)存在且极限
则称f在点x0是(1)-可微的;
(2)对于足够小的h>0,存在f(x0)-Hf(x0+h)和f(x0-h)-Hf(x0)使得
则称f在点x0是(2)-可微的。
当f在点x0是(1)-可微或(2)-可微时,则称f在点x0是强广义可微的。

引理2[5]非线性模糊Volterra积分微分方程
(1)
等价于下列模糊积分方程之一,其中f,k为模糊函数:
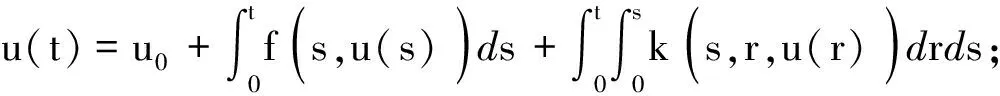

2 主要结果

(2)
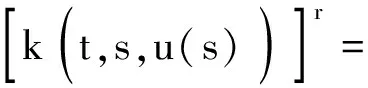
(3)
进一步,若u(t)是定义1中的(1)-可微,将方程(1)转化为:
(4)
若u(t)满足定义1中的(2)-可微,将方程(1)转化为:
(5)
利用方程(2)和方程(3),不难将方程(1)转化为:
(6)
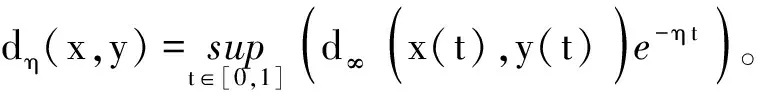
下面的定理见文献[5],本文采用与文献[5]不同的方法给予证明。
定理2假设f∶[0,1]×C([0,1],RF)→RF,k∶[0,1]2×C([0,1],RF)→RF连续。若存在常数L1,L2>0,使得:


则方程(1)对每种可微性在[0,1]上都有唯一解。
证明假设方程(1)是(1)-可微的,任给u∈RF,t∈[0,1],定义算子G如下:
那么G∶C([0,1],RF)→RF连续,且对给定的t0∈[0,1],有
G∶C([t0,t0+a],RF)→C([t0,t0+a],RF),这里0 对于每一个u,v∈C([t0,t0+a],RF),且u≤v,由Hausdorff距离的性质,有 若方程(1)是(2)-可微的,证明类似。证毕。 定理3设f∶[0,1]×RF→RF,k∶[0,1]2×RF→RF满足如下条件: (ii)存在L1,L2>0,使得 对所有r∈[0,1]都成立,则方程(1)与方程(6)等价。 下面考虑方程(1)是带三角模糊初值条件的情形:其中 (7) (8) 将方程(1)转化为下列积分微分方程组: (9) 故方程(1)和方程(9)均存在唯一解。由于方程(9)等价于积分方程: 本文给出了非线性Volterra模糊积分微分方程解存在唯一性的充分条件和解析解的表达形式,研究过程是先给出非线性Volterra积分微分方程的两种特征定理,并利用特征定理将其转化为积分微分方程组,然后验证方程组的解的存在性。下一步将研究高阶Volterra模糊积分微分方程的求解方法。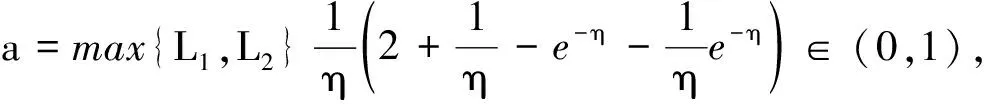

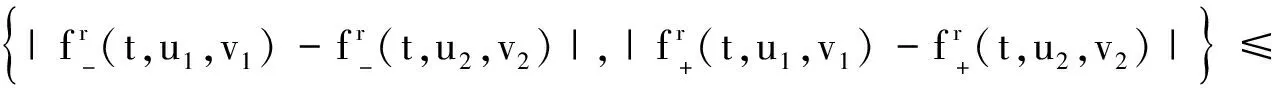
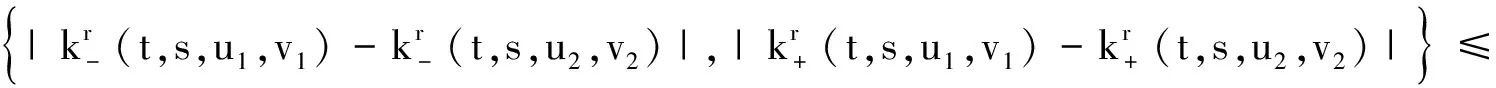


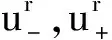

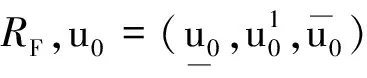
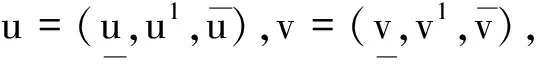

3 结束语
