矩阵对数公式及其应用
2020-06-08李婉,张林
李 婉,张 林
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
量子信息科学是近年来兴起的一门量子力学与信息学的交叉学科。“熵”作为量子信息中的一个重要概念,用来度量系统状态的不确定性,在量子信息论、量子计算、量子通信中均有广泛应用。而量子态的冯·诺依曼熵与相对熵的定义[1]都涉及矩阵对数的计算,所以关于矩阵对数的研究非常有意义。文献[2]提出并非所有矩阵都存在矩阵对数,矩阵存在对数的充要条件为该矩阵可逆,且可逆矩阵的对数不唯一;文献[3]提出无负实数特征值的可逆矩阵存在唯一的矩阵对数,特别地,正定矩阵存在唯一的矩阵对数。而关于矩阵对数的计算已有众多研究,文献[4]针对k-循环矩阵、斜k-循环矩阵、Hermitiank-循环矩阵三类循环矩阵给出矩阵对数的算法;文献[5]提出一种计算主矩阵对数的Fibonacci-Horner和多项式分解的方法;但这些结果仍未给出具体的矩阵对数计算公式,文献[6]针对集合{I(1-t)+At∶t∈[0,1]}(I为单位矩阵,A为任意实矩阵)中的矩阵给出其主矩阵对数的显式多项式公式。本文则针对有限阶具有互异特征值的正定矩阵给出矩阵对数公式,将矩阵对数仅表示成有限个矩阵幂的线性组合的形式。
1 n阶正定矩阵的对数公式
本文的矩阵对数是指函数演算意义下的矩阵对数。具体而言,对于n×n阶正定矩阵A,设a1,a2,…,an为其特征值,diag(a1,a2,…,an)表示以a1,a2,…,an作为对角元的对角矩阵。存在酉矩阵U,使得A=Udiag(a1,a2,…,an)U-1,则矩阵对数ln(A)按如下方式计算:
下面给出的矩阵对数公式将矩阵对数表示为有限个矩阵幂的线性组合,线性组合的系数仅与矩阵的特征值有关。
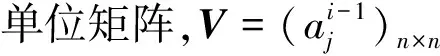
ln(A)=α0In+α1A+…+αn-1An-1
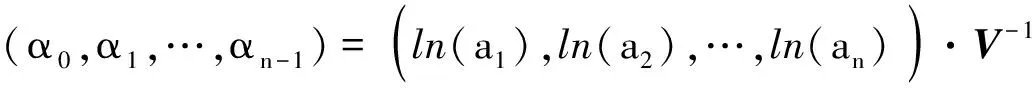
证明若pA(x)=det(xIn-A)=xn+c1xn-1+c2xn-2+…+cn-1x+cn为矩阵A的特征多项式,则由Cayley-Hamilton定理[7],可得:
pA(A)=An+c1An-1+c2An-2+…+cn-1A+cnIn=0
即In,A,A2,…,An线性相关。又由矩阵A有n个互异的特征值,易知In,A,A2,…,An-1线性无关,则可设
E=ln(A)=α0In+α1A+…+αn-1An-1
(1)
在式(1)两边依次左乘矩阵A,A2,…,An-1,对所得矩阵方程组的各式两边取迹有
即有
(2)
又由a1,a2,…,an为矩阵A的n个特征值,有
(3)
联立式(2)、式(3),可得:
(4)


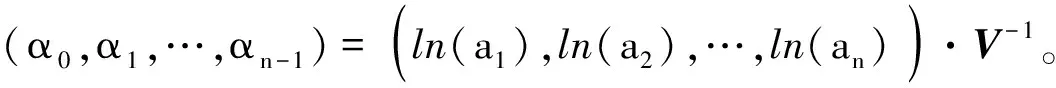
量子态的冯·诺依曼熵与相对熵的定义均涉及矩阵对数的计算,有了上述正定矩阵的矩阵对数公式,下面给出量子比特的冯·诺依曼熵与相对熵的新的表示。
2 量子比特的熵与相对熵
在量子信息中,量子态的数学描述为密度矩阵,即迹为1的半正定矩阵。下面给出n阶量子态的冯·诺依曼熵与相对熵的定义。
定义[1]对于给定的n阶量子态ρ和σ,ρ的冯·诺依曼熵定义为:
S(ρ)=-Tr(ρlnρ)
(5)
ρ和σ的相对熵定义为:

(6)
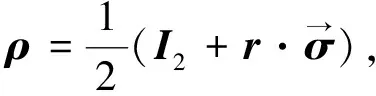
量子态冯诺依曼·熵的计算在量子信息中具有重要的应用,比如量子Jensen-Shannon散度[8]作为混合态之间区分度的一种测量,其定义涉及到量子态的冯·诺依曼熵的计算。下面利用量子比特态的Bloch表示给出量子比特态的冯·诺依曼熵与相对熵的简单表示。
推论1对于量子比特态ρ,记其Bloch矢量的长度为r。若0 ln(ρ)=α0(r)I2+α1(r)ρ (7) 推论2ρ,σ为2个量子比特态,记ρ,σ的Bloch矢量分别为r=(r1,r2,r3),s=(s1,s2,s3),ρ,σ的Bloch矢量的长度分别为0 (1)ρ的冯·诺依曼熵为 (2)ρ,σ的相对熵为 其中,α0(r),α0(s),α1(r),α1(s)由推论1给出,〈r,s〉=r1s1+r2s2+r3s3表示向量内积。 证明由推论1,有 ln(ρ)=α0(r)I2+α1(r)ρ,ln(σ)=α0(s)I2+α1(s)σ, 将ln(ρ),ln(σ)代入式(5)易得S(ρ)。将ln(ρ),ln(σ)代入式(6),有 证毕。 本文主要研究任意有限阶具有互异特征值的正定矩阵的对数公式,并利用二阶正定矩阵对数公式及二阶量子态的Bloch表示给出量子比特的冯·诺依曼熵与相对熵的新的表示。本文得到的矩阵对数公式形式简单具体,便于进行含有矩阵对数的量之间的运算。量子比特的熵与相对熵的新的表示为二阶量子态的熵的相关运算提供更多便利。在此基础上,继续研究量子比特态的量子Jensen-Shannon散度新的表示,从而进一步研究其下边界。
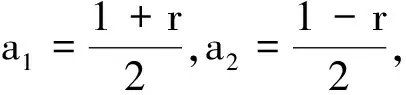
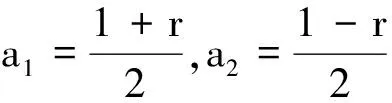

3 结束语
