具有死区输入时滞大系统的实际跟踪问题

赵子恒，贾祥磊，周绍生

(杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

过去几十年中，大系统的研究一直是热门研究之一。关于大系统的研究多以镇定问题为主，如文献[1]提出一种基于观测器的分散输出反馈控制方案，研究一类大型前馈非线性时滞系统的分散镇定问题。对于跟踪问题，大多以单输入单输出系统为研究对象，如文献[2]研究一类不确定非线性系统的输出反馈全局实际跟踪问题。针对一类具有时滞零动态的不确定非线性时滞系统，文献[3]通过结合通用控制和死区思想，解决了输出反馈全局跟踪的问题。然而，关于多输入多输出(Multiple-Input Multiple-Output，MIMO)的大系统跟踪问题的研究成果相对较少。如文献[4]引入辅助设计系统分析输入约束的影响，针对MIMO大系统提出一种自适应跟踪控制方法。而考虑到系统中出现死区输入非线性的情况，仅有文献[5]通过引入一种新的光滑死区逆，提出一种分散自适应控制方案，解决了一类时滞大系统的输出跟踪问题，但由于反推法的引入，证明过程较为复杂。最近，文献[6]研究了一种具有死区输入的情况，所提出的方案避免了复杂的推导过程，但只考虑单输入单输出且不受时滞影响的非线性系统。受文献[6]启发，本文结合文献[7]中对高增益观测器和非分离原则的研究以及文献[8]中对未知有界扰动情况的研究，将文献[6-8]中增长条件的限制推广到MIMO系统中，进而解决一类具有死区输入MIMO非线性时滞系统的全局实际输出反馈跟踪问题。

1 系统描述

由N个子系统组成的非线性时滞大系统如下：

(1)

(2)

式中，mri>0，mli>0和bri>0，bli>0分别是第i个死区输入的死区斜率和死区断点。

为构造时滞无关输出反馈控制器，引入如下技术假设及引理。

假设1执行器输出ui是可测量的。

假设2死区参数mri，mli，bri和bli属于某个紧集[a,b]，其中a，b是未知正常数。

(3)

|x+y|p≤2p-1|xp+yp|

引理2[9]对任意正实数m,n和实值函数α(x,y)>0，如下不等式成立：

引理3[10]存在向量Hi=[hi,1…hi,ni]T，Ki=[ki,1…ki,ni-1]和对称矩阵Pi>0，Qi>0满足：

Pi(Ai-HiCi)+(Ai-HiCi)TPi≤-Ini,PiDi+DiPi≥Ini
Qi(A′i-B′iKi)+(A′i-B′iKi)TQi≤-2Ini-1,QiD′i+D′iQi≥Ini-1

(4)

Ci=[101×(ni-1)],Di=diag{σ,σ+1,…,σ+ni-1},D′i=diag{σ,σ+1,…,σ+ni-2}。其中σ>0是任意常数，Ini是ni×ni维的单位矩阵。

2 主要结果

定理1若非线性时滞大系统(1)满足假设1—4，则如下动态输出反馈控制器，可实现闭环系统的全局实际跟踪：

(5)

证明首先，将非对称死区模型重新表示为如下形式：

ui=Ni(vi)=ρi(vi)vi+ϖi(vi)

(6)

(7)

引入如下坐标变换：

(8)

进一步可以得到：

(9)

式中，εi=[εi,1…εi,ni]T，H′i=[hi,1…hi,ni-1]T，Φi=[φi,1…φi,ni]T，并且有：

(10)

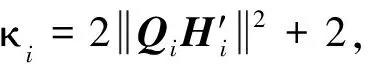
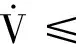
(11)

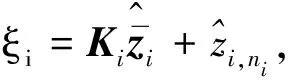
(12)

式中，θ4，θ5和θ6是未知的正常数。结合反推法思想，构造如下Lyapunov-Krasovskii泛函：

(13)

式中，γ=θ4+1，对式(13)求导并结合式(5)化简可得：

(14)

由式(14)可以推出如下引理：

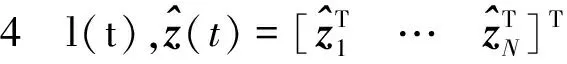
证明分3部分证明引理4，定义一个通用的常量ϑ，它表示一个有限的正常数，并可能在不同的地方被隐式地更改。

l-2γθ3≥1

(15)

(16)

(17)

(18)

(19)

(20)

最后，证明ε(t)的有界性。选择常数l*满足l*>max{l(tf)，2+ϑ+λmax(Pi)}，引入坐标变换：

(21)

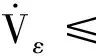
(22)

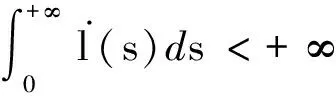
(23)

结合l的有界性可得出每一个子系统的跟踪误差yi-yir将会进入并永远停留在区间(-λ,λ)的范围之内，而λ则是提前给定的任意小的正数。

3 数值示例

由具有相互连接的时滞循环流的2个化学反应器组成的大型系统[11]如下：

(24)

图1 系统1状态与观测器轨迹

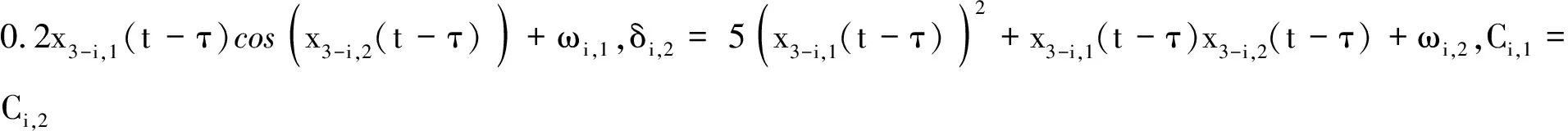
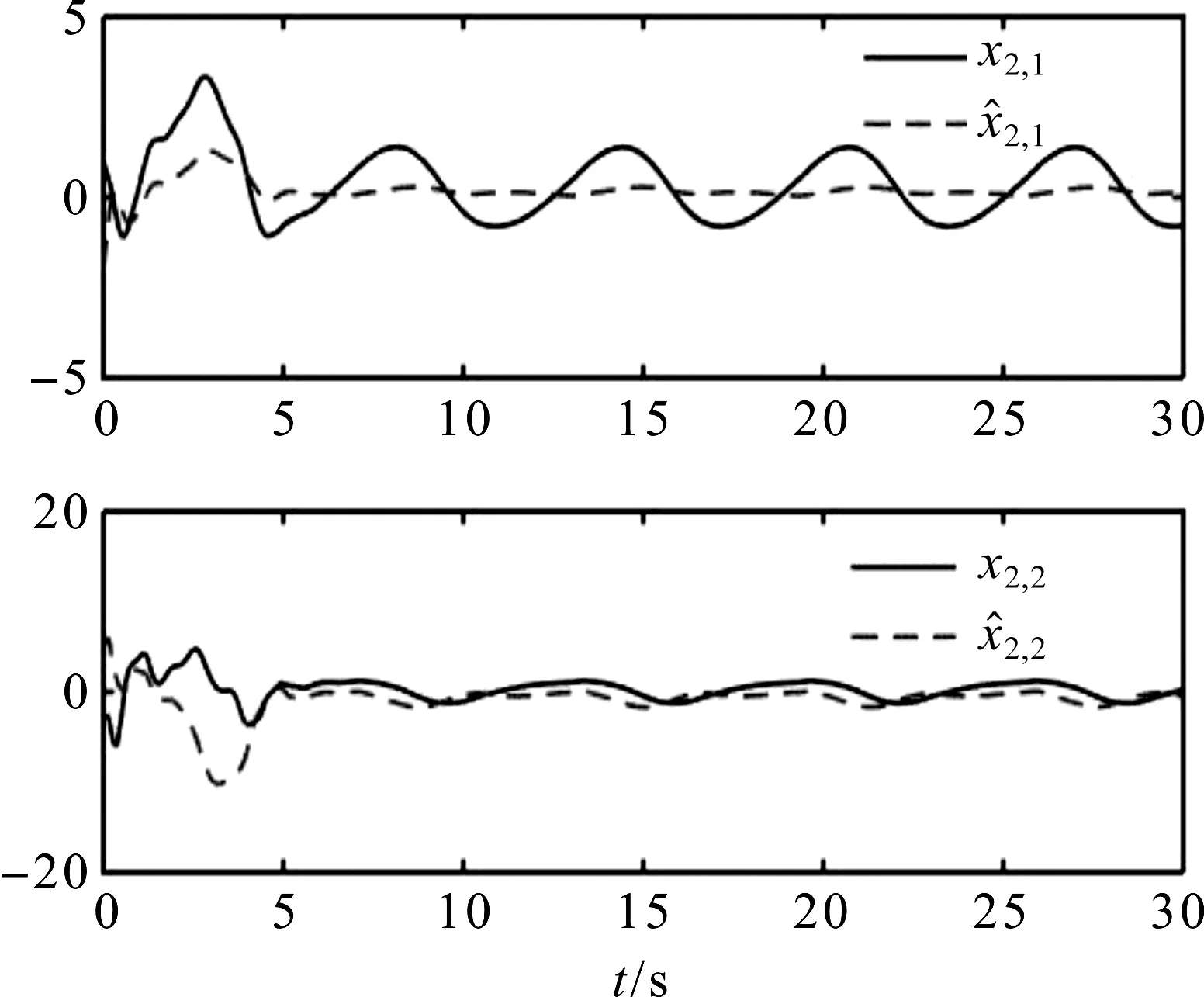
图2 系统2状态与观测器轨迹

图3 各执行器输入输出轨迹

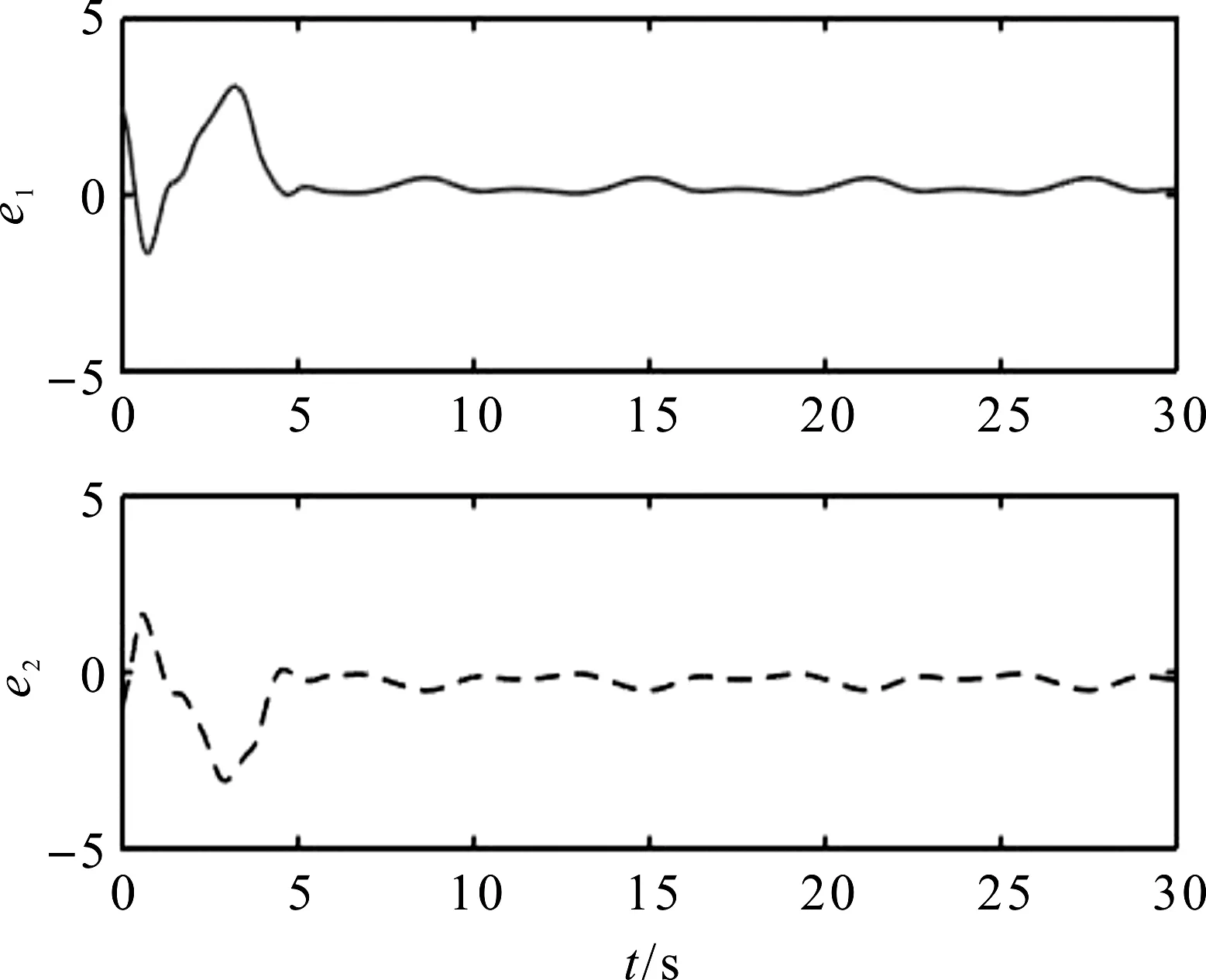
图4 系统跟踪误差e1与e2轨迹

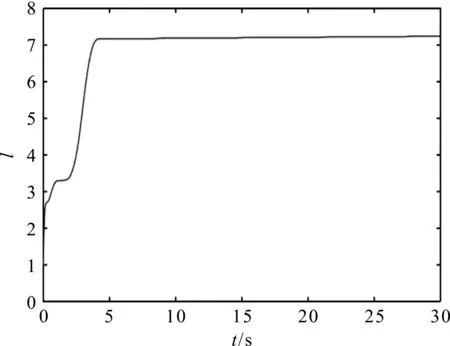
图5 动态高增益l轨迹

从以上仿真结果可以看出：经过一段时间后，系统的所有状态都是有界的，且跟踪误差均保持在给定的λ=0.8之内，即(-0.8,0.8)区间内，从而验证了本文方案的可行性。

4 结束语

本文主要研究带有死区输入的非线性时滞大系统的实际跟踪问题，提出一种具有自适应增益的输出反馈控制器。相比较现有文献，本文使用的一步反推法能解决一般反推法无法避免的复杂的计算度问题，为其他相关研究提供了一种新的思路。目前，本文仅考虑了系统中具有死区输入约束特性的情况，后续将对具有其他输入约束特性(如饱和输入，磁滞输入等)的系统进行自适应跟踪控制研究。