固体发动机推进剂/衬层粘接试件振动损伤分析

2020-06-08李金飞宋佳明

指挥控制与仿真 2020年3期

刘磊，李金飞，宋佳明

(海军航空大学岸防兵学院，山东烟台 264001)

固体发动机作为一种长寿命、可靠性较高的军工产品，其在正常振动环境下的失效时间以年为计数单位，模拟正常海洋值班环境下的振动试验需要较长的试验周期、较高的费用和人力成本。研究表明，界面脱粘是影响发动机寿命的主要因素之一［1］。想要探究固体发动机长时间值班过程中推进剂/衬层粘接界面的损伤规律，有必要进行实验室振动加速试验［2］。加速试验可以加快产品破坏，大幅减少试验周期，节约大量成本，且选择合理的加速模型能很好地得到对应实际环境下的损伤规律［3-4］。

为了研究不同频率和振动时间对推进剂/衬层粘接界面力学性能的影响，笔者开展了粘接试件的振动加速试验和单向剪切拉伸试验，应用双因素方差分析法对试验频率和振动时间对试件粘接强度的影响结果进行了检验。

1 试验准备

1.1 粘接试件制备

参考航天工业标QJ2038.2—91《固体火箭发动机燃烧室界面粘接强度测定方法》［5］的有关要求，本文设计了推进剂/衬层粘接试件，试件尺寸如图1所示。试验采用的粘接试件由金属件、绝热层、衬层及推进剂组成。粘接试件的推进剂选用HTPB复合推进剂，其组分包含质量百分比为10%的黏合剂、14%的铝粉颗粒、69%的AP(高氯酸铵)颗粒以及7%的添加剂。

图1 粘接试件

1.2 试验设备

本次试验采用的设备有ES-10-240/Amber振动试验系统和CMT6203电子万能试验机，如图2所示。振动试验系统用于开展振动加速试验，电子万能试验机用于开展单向剪切拉伸试验。

图2 试验设备

1.3 单向拉伸夹具设计

为实现对粘接试件的剪切拉伸，本文设计了组合夹具，该套夹具能实现多角度拉伸，其设计尺寸如图3所示。组合夹具由接头和夹盘两部分组成，接头用于连接拉伸机凸轴和夹盘，夹盘用于固定和拉伸粘接试件。

图4显示了拉伸夹具在试验机上的装配，上下夹盘各开有一个通孔，粘接试件的两个钢柱穿过通孔，用螺母紧固在夹具上。试验时，上半部分夹具随拉伸机竖向移动，下半部分夹具固定。

2 试验方案

在装夹粘接试件时，将试件两端通过组合夹具固定在试验台上，如图5所示。静止时，推进剂/衬层两端的粘接界面承受的剪应力均由中间推进剂部分的重力引起。

对安装在试验台上的粘接试件进行受力分析，如图6所示，设中间推进剂质量为m，界面处的剪应力为τm(t)，静止时，由力的平衡公式，有

试验时，设振动台施加的瞬时加速度为S -N，由牛顿第二定律，有

设粘接界面面积为A，材料力学中剪应力定义公式为

将式(3)代入式(2)，移项并化简，得到剪应力与加速度的转化关系式如式(4)。

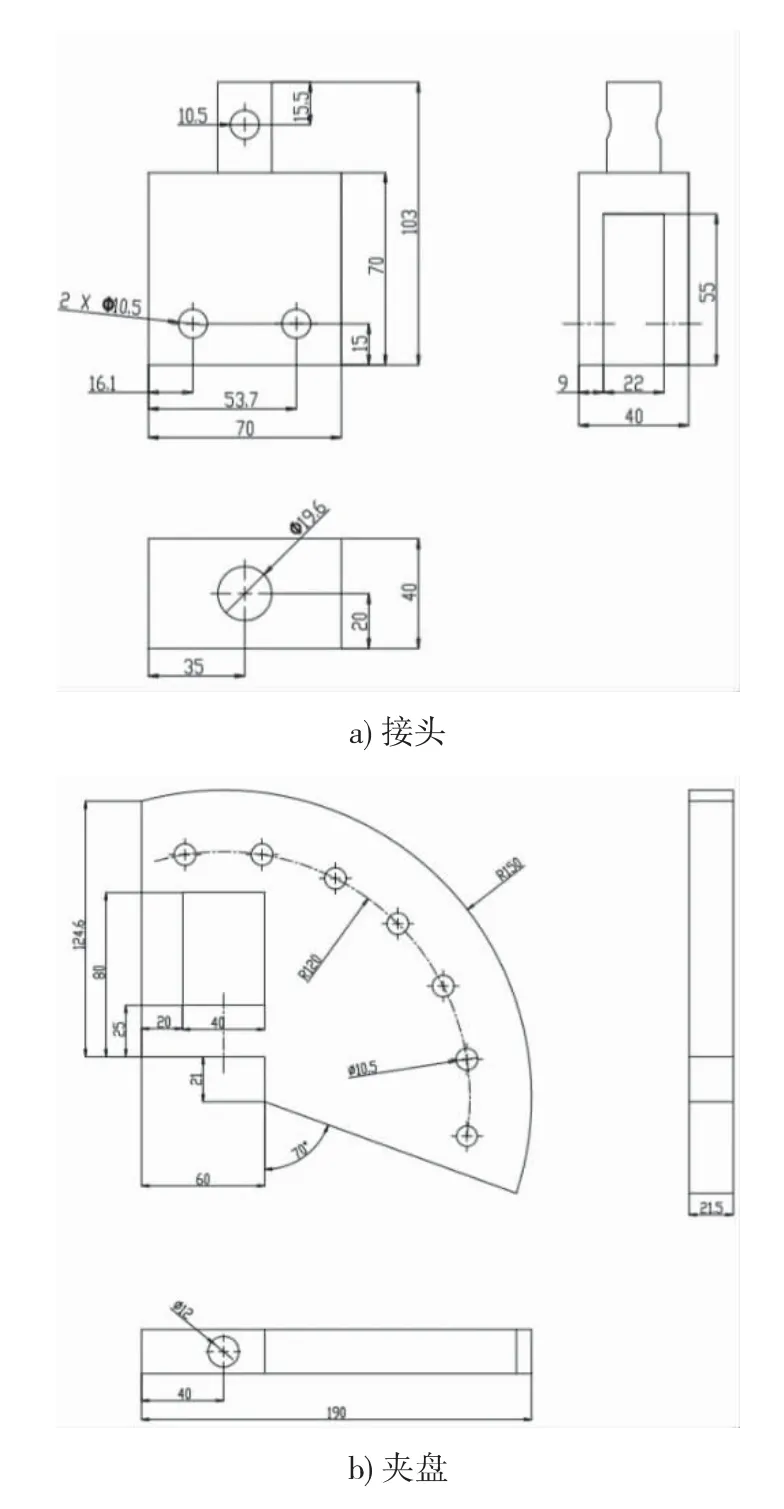
图3 拉伸夹具

图4 拉伸夹具装配图

文献［6］通过对某固体发动机在某特定海况下的振动进行有限元仿真，得到了推进剂/衬层粘接界面危险点的剪应力变幅时程，如图7所示。

图5 安装试件

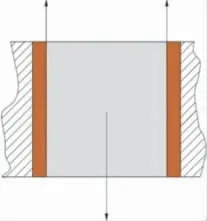
图6 粘接试件受力分析

图7 界面剪应力变幅

取同批粘接试件进行测试，得到推进剂部分的平均质量m为12.7 g，试件的平均有效粘接面积A为4 cm2。将图7中的剪应力变幅、推进剂质量m及有效粘接面积A代入式(4)，得到原始的等效加速度谱，如图8所示。

在Amber控制系统中设置随机振动参数时，要求输入的载荷为功率谱密度(PSD)。功率谱密度代表了随机信号在单位频带内的功率，其定义为

式中，S -N为自相关函数。

将时域数据代入式(5)，得到的功率谱密度结果是一条谱密度值-频率关系曲线，如图9所示。

图8 试件加速度

图9 PSD曲线

从图9可知，加速度信号的功率主要集中在0.3 Hz-0.4 Hz之间，其他频率范围内的功率谱密度值极小。在进行振动试验时，可忽略功率较小的频率，仅在振动系统中输入功率集中的部分。

由于振动试验系统最小的试验频率为5 Hz，远大于PSD谱中主要信号功率所在的频率范围，因此，必须对试验谱的频率成分进行扩大，才能开展振动加速试验。按照振动次数等效的原则，对PSD谱中的频率成分进行扩大［7］。原始加速度谱的主要功率集中在0.3 Hz-0.4 Hz频率范围内，将该频率段称为1倍频，将PSD谱频率成分扩大后的频率范围称为多倍频。计划模拟连续值班180天(d)的振动情况，每天振动24小时(h)，对应的理论振动总时间t总为180 d×24 h=4 320 h。由于振动台连续工作时间的限制，每天开展振动试验2 h，则不同倍频下对应的试验天数如下［8］

式中，ti表示不同倍频试验对应的时间，d;Δf表示一倍频的频率范围，Hz;Δfi表示多倍频的频率范围，Hz。

为探究不同振动频率对试验结果的影响，综合考虑了振动试验开展的时间长短，以及对试验天数的取整，设置了三组加速频率:108倍频、216倍频和360倍频。实验室振动加速试验时间与理论值班时间的对应关系如表1所示。

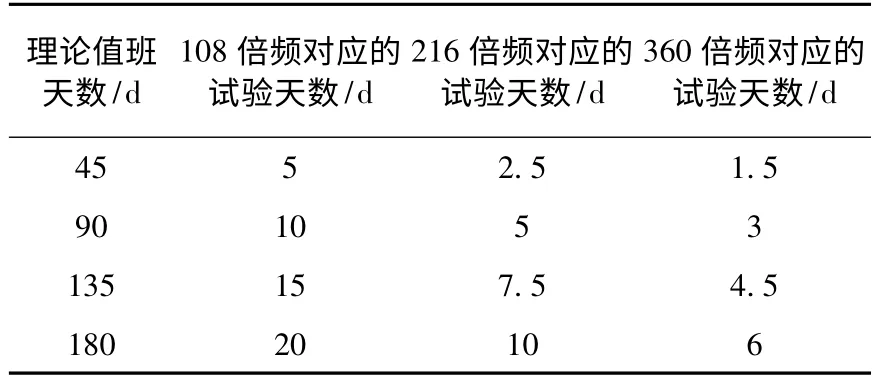
表1 理论值班时间与试验时间对照

每当试验完成四分之一进程时，分别取出部分粘接试件，进行单向剪切拉伸试验，记录试件的最大剪应力强度数据。

3 试验结果与分析

3.1 未振动试件初始性能测试

为了获取粘接试件的初始力学性能，本文首先对未振动的试件开展了单向拉伸剪切试验。根据材料力学相关原理，剪应变定义公式如下

式中，l为拉伸过程中的切向位移;H为两相界面之间的宽度。

通过单向剪切拉伸测试，得到推进剂/衬层粘接试件的τ -γ 曲线如图10所示。试件的平均最大初始剪应力τmax为318.2 KPa，对应的平均初始最大剪应变γmax为0.292。

图10 粘接界面剪应力-剪应变曲线

3.2 振动后试件拉伸结果分析

表2给出了108倍频、216倍频、360倍频三种试验方案对应的试验结果的表示方法，图11给出了试件最大剪应力-最大剪应变测试结果。

从图11可以看出，在同一倍频下，推进剂/衬层粘接试件承受的最大剪应力强度随理论振动时间的增加而减小，对应的最大剪应变同样随振动理论时间增加而减小，这说明持续振动削弱了界面抵抗变形的能力。图11无法直观地判断不同倍频对试验结果是否有影响，也难以判断最大剪应力强度与振动时间的关系，因此，使用有交互作用的双因素方差分析模型对试验数据进行分析。

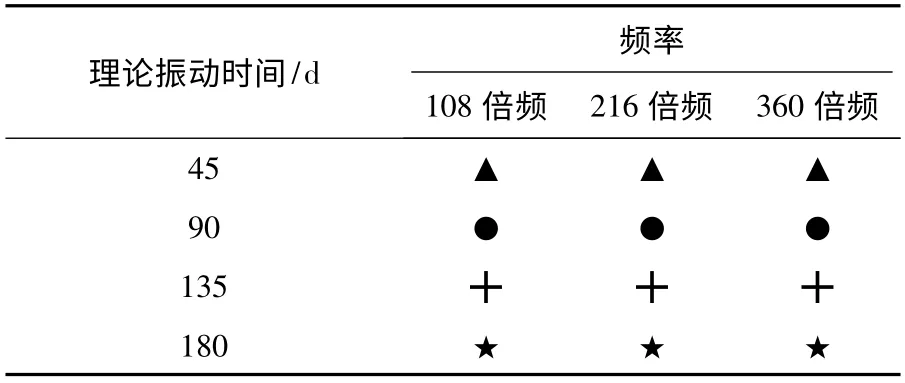
表2 不同试验结果的表示方法

图11 单向拉伸测试结果

设理论值班时间为因素A，试验振动频率为因素B，因素A有45 d、90 d、135 d、180 d四种不同水平，因素B有108倍频、216倍频、360倍频三种不同水平。双因素方差分析模型如下:

式中，ξijk为不同试验测得的数据值;μ 为试验总体数据的数学期望均值;αi为因素A的第i个水平对试验的影响;βj为因素B的第j个水平对试验的影响;εijk为试验误差产生的随机变量。

检验理论振动时间、频率以及交互作用对试验结果的影响程度，首先需要假设三种因素对试验结果均无显著影响，分别用H01、H02、H03表示，然后使用F检验法对假设进行检验:

若FA≥F1-α((r -1，rs(t -1))，则拒绝H01，否则接受H01;

若FB≥F1-α((s -1，rs(t -1))，则拒绝H02，否则接受H02;

若FA×B≥F1-α((r -1)(s -1)，rs(t -1))，则拒绝H03，否则接受H03。

使用统计学软件Spss进行双因素方差的分析，将试验结果输入软件中，设置振动频率为主体内因子，振动时间为主体间因子。首先对数据进行球形度检验，检验结果如表3所示。

表3 Mauchly球形度检验

从表3的检验结果看，显著性p值为0.203＞0.05，满足球形假设，不需要对自由度进行校正。满足球形假设后，对A、B两种因素进行方差检验，结果分别如表4和表5表示。

表4 主体内效应的检验

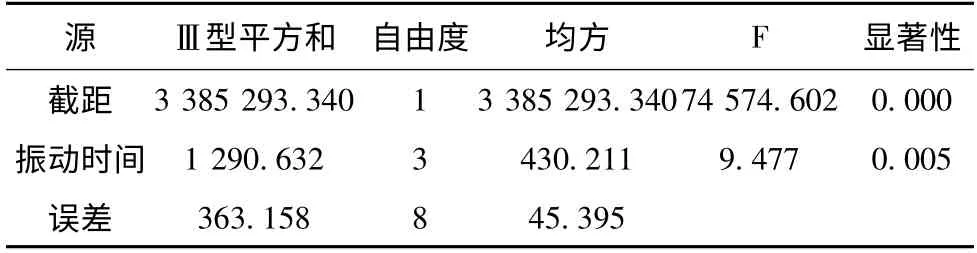
表5 主体间效应的检验

从主体内效应检验结果看，频率因素B的显著性p值为0.871＞0.05，频率和振动时间交互作用因素的显著性p值为0.999＞0.05，因此，接受原假设，认为不同的试验频率、振动时间和频率的交互作用均对试验结果不具有显著影响。

从主体间效应检验结果看，振动时间因素A的显著性p值0.005＜0.05，因此，否定原假设，认为振动时间对试验结果具有显著性影响。

综合来看，理论振动时间与振动频率之间不存在明显的交互作用;当以理论振动时间作为衡量尺度时，不同频率下的振动试验对推进剂/衬层粘接试件最大剪应力强度的影响无明显区别;探究振动时间对试件力学性能的影响，需要进一步查看估计边际均值的结果。

图12给出了振动时间和频率双因素作用下的最大剪应力强度估计边际均值曲线。

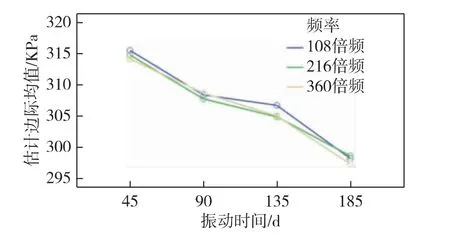
图12 振动时间* 频率估计边际均值曲线

从图12的结果看，在理论振动时间45 d、90 d、135 d、180 d四种水平下，三种试验频率对应估计边际均值的最大差值分别为1.4 KPa、0.9 KPa、1.8 KPa和1.3 KPa。三种不同频率下最大剪应力强度的估计边际均值随振动时间的曲线变化趋势相同，从原始未振动状态至理论振动180天时，108、216、360倍频的估计边际均值较初始最大剪应力强度分别下降了6.24%、6.15%和6.56%。