灰色系统理论在预应力混凝土连续梁桥施工中的应用
2020-06-07廖一汉
廖一汉
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
0 引 言
自20世纪90年代开始,灰色系统理论被应用于大跨径桥梁的误差预测控制中[1]。灰色系统是信息不完全、不确定的系统,它是以灰关联空间为基础的分析体系[2]。以现有的信息或原始数列为基础,通过灰过程及灰生成对原始数列进行数据加工处理,建立灰模型(GM模型)体系,来预测系统未来的发展变化[3]。利用灰色理论来对箱梁立模标高进行预测与修正时,通过确定已完成号块主梁的测量值与计算值之间的误差,结合结构原有的系统关系,估计主梁高程误差未来的发展规律,确定对现在误差的调整量,其最大特点是应用灰色模型而不是对系统内各项因素的分项分析,换句话说,灰色控制不追求模型本身的问题,而是从总体误差上进行控制,只关心控制的最终结果,是反馈控制的一种变化应用[4-6]。
桥梁结构作为一种非线性结构[7],在施工过程中会受到材料性能、混凝土收缩徐变、施工荷载、温度及环境等其他多种因素影响。因此,需要通过对施工过程不断地监测、识别,并对关键参数进行预测,及时调整施工工序,从而保证桥梁结构的安全性和可靠性[8,9]。
1 灰色系统理论的计算原理
桥梁施工过程可以看作是一个受噪声干扰的随机系统,灰色系统理论将这一切随机变量看作变化的灰色量,将这一随机过程看作随时间变化、在一定控制范围内的灰色过程,把杂乱的原始数据整理成规律性强的生成数列进行数据生成。本文选用单个变量的GM(1,1)模型对桥梁标高调整误差的预测进行分析。
建立GM(1,1)模型:
x=x(x(1),x(2)…x(n))
(1)
y=y(y(1),y(2)…y(n))
(2)
式中:x为理论挠度变化值序列;y为实测挠度变化值序列;x(k)为第i号已浇筑梁段理论挠度变化值;y(k)为第i号已浇筑梁段实测挠度变化值。
建立误差序列:
δ(i)=x(i)-y(i)i=1,2,3…n
(3)
x(0)(k)=δ(i)+Ci=1,2,3…n
(4)
令x(0)为N元原始建模序列
x(0)={x(0)(1),x(0)(2),…,x(0)(n)}
(5)
x(1)为x(0)的一次累加序列其中,
(6)
于是GM(1,1)白化形式的微分方程为:
(7)
式中:a、μ为待定参数。
将式(7)白化微分方程离散化,再通过一次累减生成与应用某一时刻的背景值代换,最后将式(7)转化成矩阵形式,通过最小二乘法即可求得待定参数a、μ。
把a、μ带入白化微分方程(7)求出其离散解为:
(8)
经还原数据得:
(9)
所建立的GM模型在精度满足的条件下,可以预测结果。检验模型的合理性一般有3种方法,包括后验差检验法、相对误差检验法和关联度检验法,这里介绍一下后验差检验法。
(10)
由式(5)~(10)可以计算残差序列E:
(11)
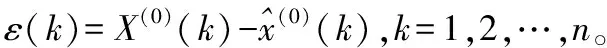
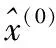
(12)
(13)
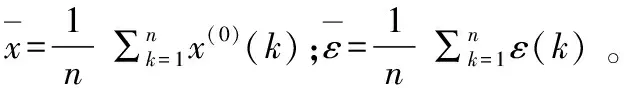
由上式可求得后验差检验的两个重要指标C、p,后验差比C如下式计算:
C=S2/S1
(14)
小误差概率p如下式计算:
(15)
GM(1,1)模型的精度由指标C、p共同确定,一般的模型级别取max{C的级别,p的级别},精度参照下表。
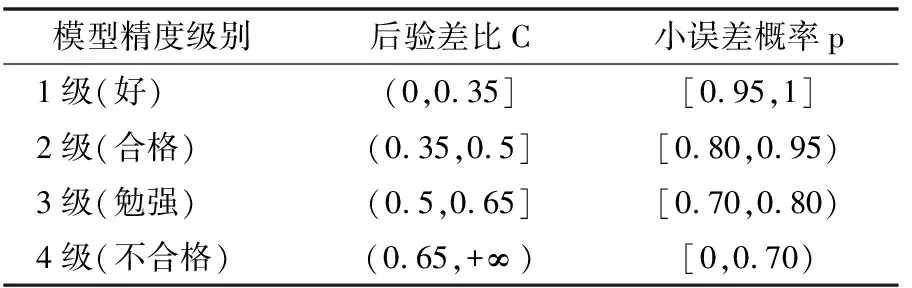
表1 后验差检验法精度参照表
2 工程概况及建立有限元模型
三元路淠河总干渠桥主桥为悬臂浇筑变高度连续梁桥,跨度布置为(46+70+42)米,桥梁全宽25.0米,按双幅设置;采用单箱单室断面。箱梁顶板宽度为12.34m,底板宽度为6.95m,腹板厚度为50.0cm,顶板厚度30.0cm,底板厚度按二次抛物线由30.0cm变化到58.6cm,箱梁根部底板边缘梁高4.79m,端部中心梁高2.19m,桥面1.5%的横坡由箱梁腹板变高度形成。
主跨上部构造按三向预应力设计,纵桥向预应力钢束设置了顶板束、底板束和腹板下弯束,采用Φs15.2高强度低松弛钢绞线,钢绞线标准强度1860MPa,采用两端张拉。纵向预应力束管道采用预埋塑料波纹管成孔,真空压浆工艺。竖向预应力采用精轧32mm螺纹钢筋,竖向预应力束(筋)管道采用预埋金属波纹管成孔。顶板横向钢束采用Φs15.2高强低松弛钢绞线,钢绞线标准强度1860MPa,采用交错单端张拉,配套扁锚体系,真空压浆工艺灌浆。
箱梁悬浇施工,箱梁浇筑分段长度依次为:9.94m(边跨现浇段)+2m(边跨合龙段)+4×4.0m+4×3.0m(8个悬浇段)+3.25m(1号块)+5.5m(0号块)+3.25m(1号块)+4×3.0m+4×4.0m (8个悬浇段)+2.0m(中跨合龙段)+4×4m+4×3.0m+3.25m(1号块)+5.5m(0号块)+3.25m(1号块)+4×3.0m+4×4.0m(8个悬浇段)+2m(边跨合龙段)+5.94m(边跨现浇段)。其中0号块、1号块段采用托架现浇施工,中跨合龙段及边跨合龙段采用吊篮施工,边跨尾段采用临时墩+支架现浇施工。
根据设计图反映的内容,对全桥总体结构建立能反映施工荷载的有限元模型,对该桥进行了正装分析,得到各阶段主梁变形状态。计算模型中根据悬臂施工梁段的划分、支点、跨中、截面变化点等控制截面将全桥箱梁段划分为103个结点和54个单元,全桥Midas计算模型如下图所示。
3 验证灰色理论的可行性
本文以三元路淠河总干渠主桥左幅1~6#块为例,在施工过程中,选择箱梁底板中点为标高的控制点,通过1~5#块箱梁浇筑张拉后实测高程与立模标高的误差,来对6#块进行预测。相关数据见表2~表5。
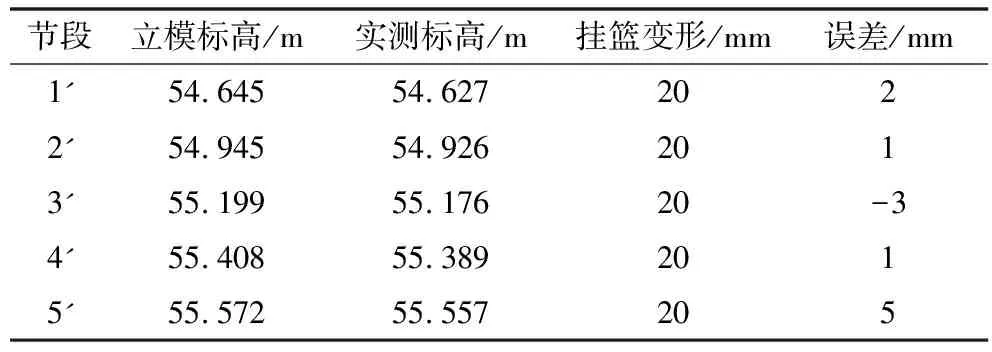
表2 9#墩小桩号方向误差原始序列值
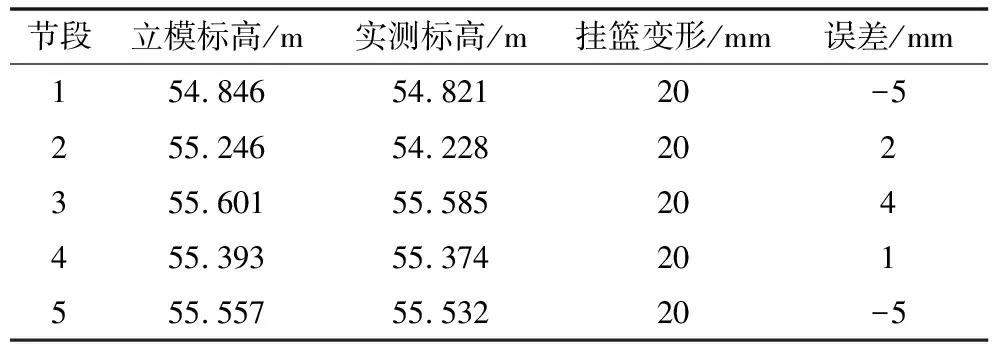
表3 9#墩大桩号方向误差原始序列值
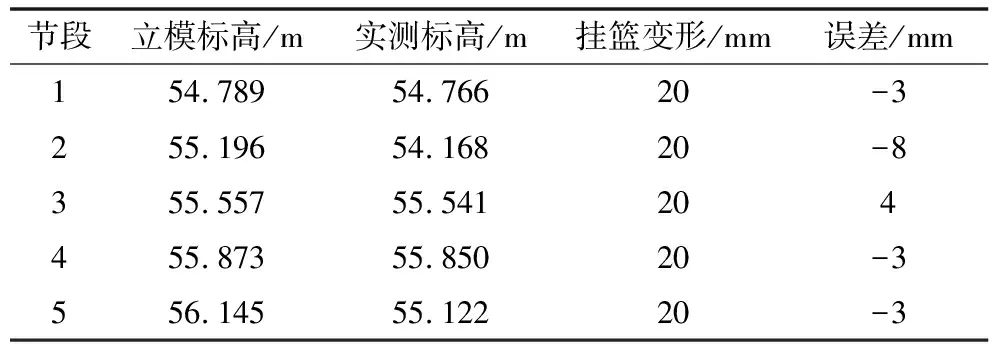
表4 10#墩小桩号方向误差原始序列值

表5 10#墩大桩号方向误差原始序列值

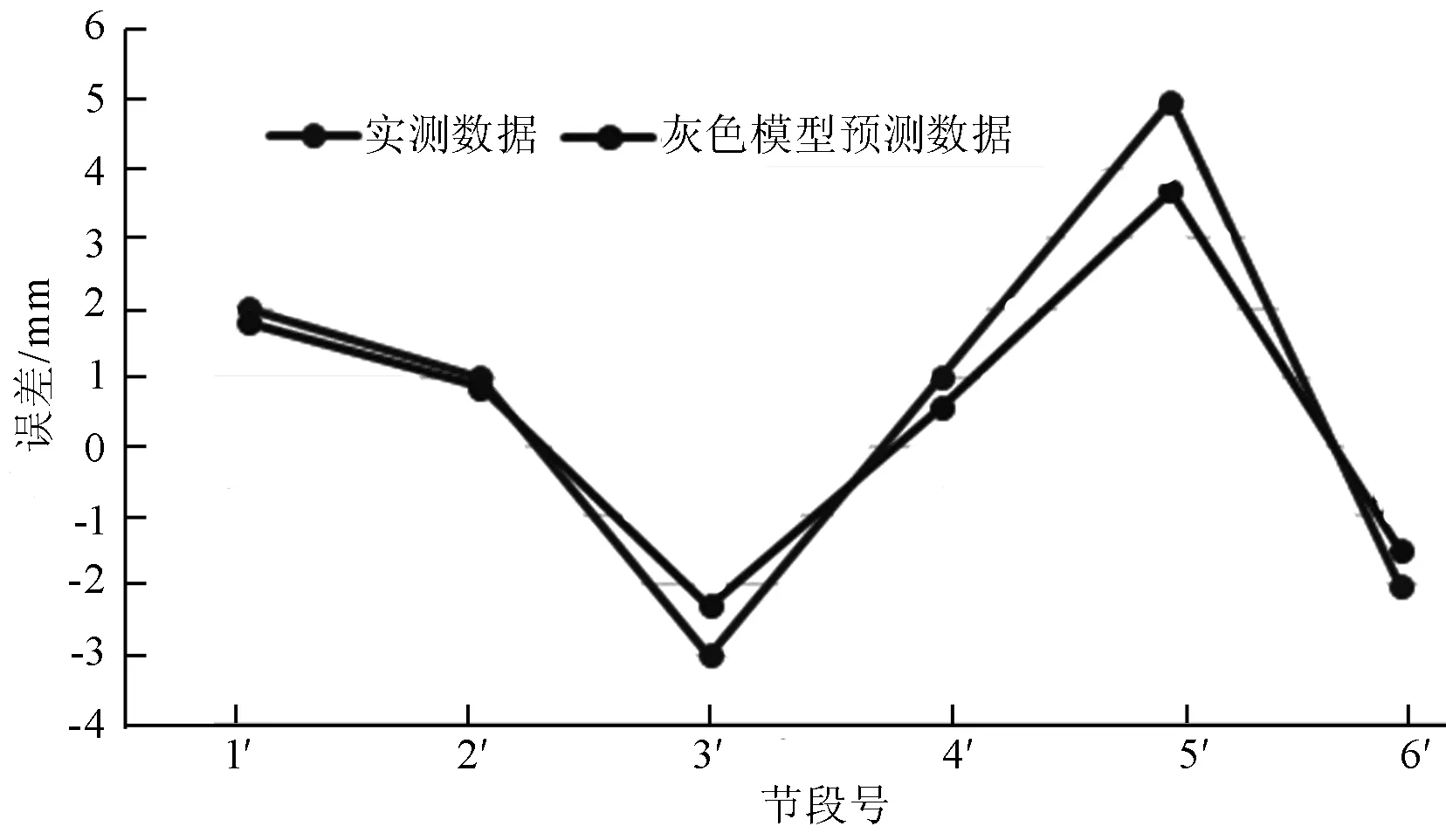
图1 9#墩小号桩号方向误差预测结果
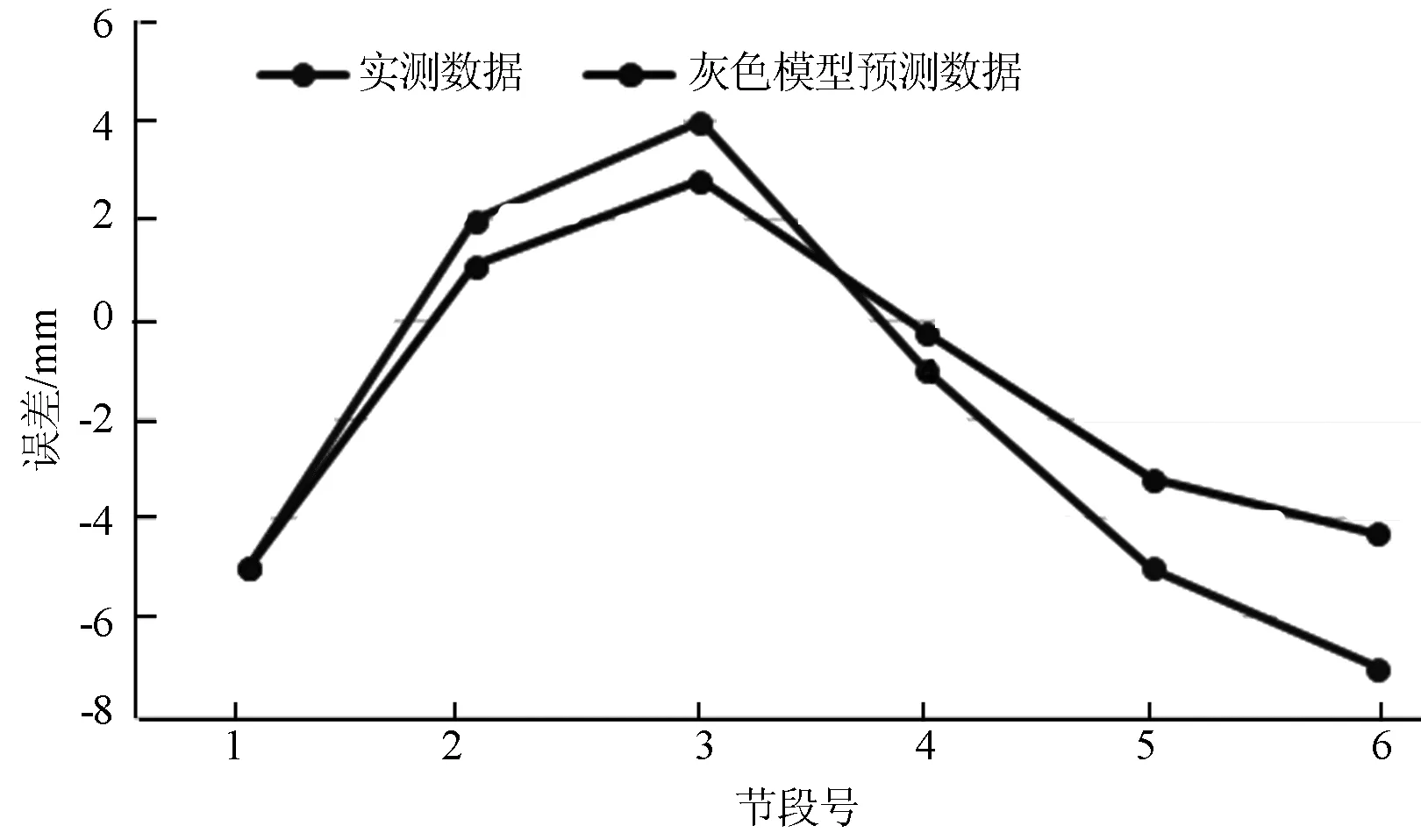
图2 9#墩大号桩号方向误差预测结果
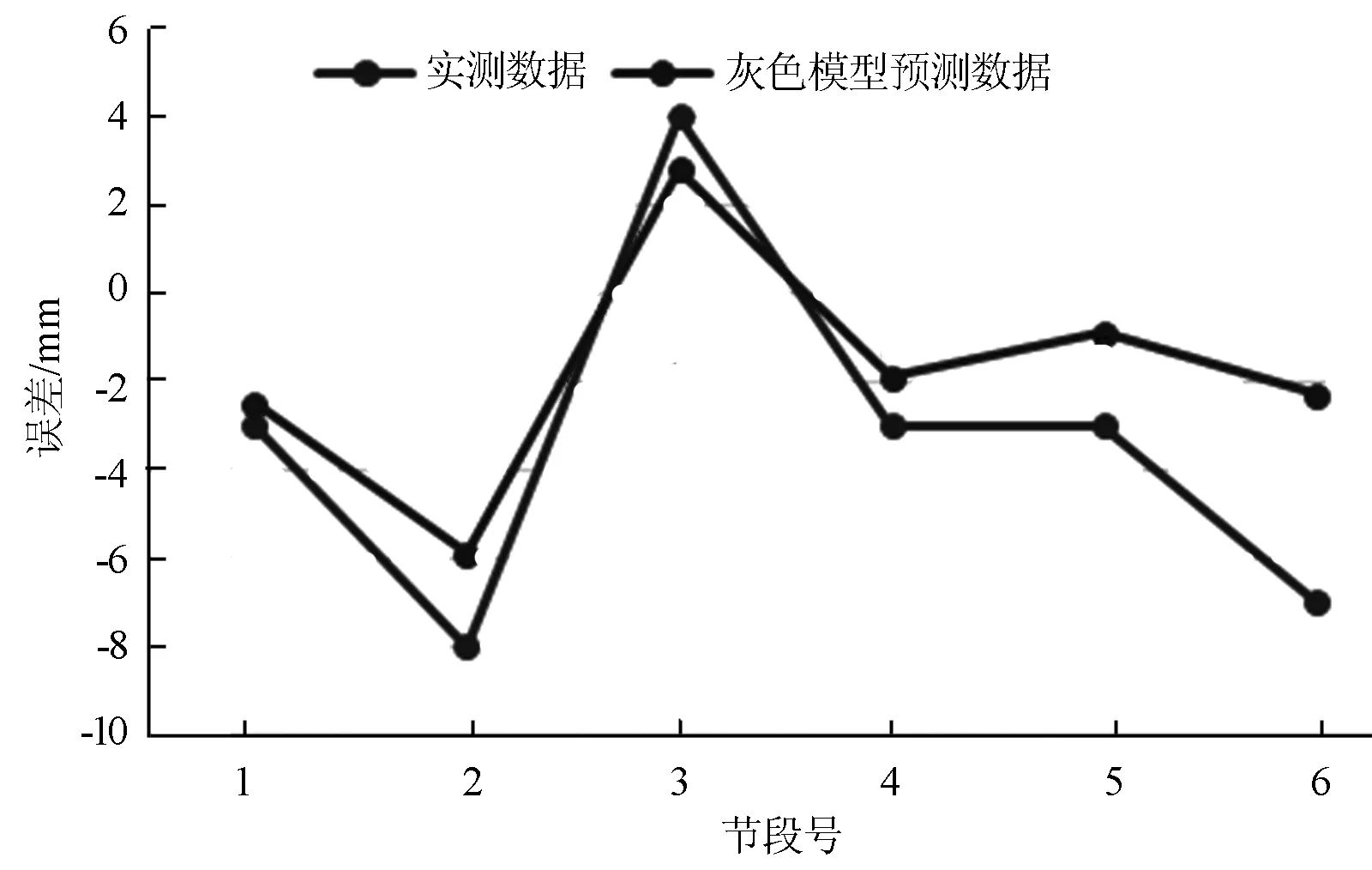
图3 10#墩小号桩号方向误差预测结果
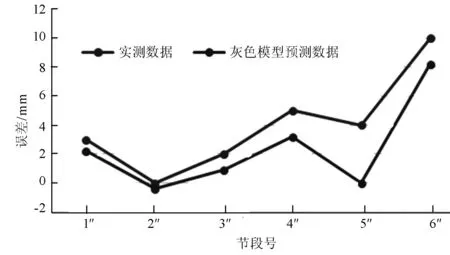
图4 10#墩大号桩号方向误差预测结果
由以上图表对比可知,采用上一阶段挠度的实测值作为灰色系统理论的初始序列,可以有效的修正下一节段立模标高与实测标高之间的误差。根据上述施工控制方案,最后得到三元路淠河总干渠桥的合龙误差汇总,见表6,合龙精度也是得到了改善。
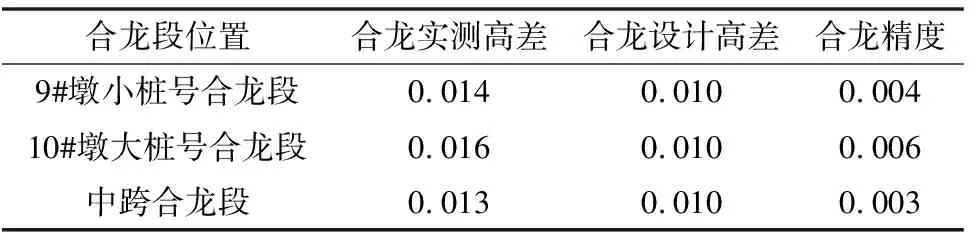
表6 左幅合龙误差汇总 (单位:m)
4 结束语
(1)本文介绍了灰色系统理论的计算原理,该理论基于将一切随机变量看作变化的灰色量,将这一随机过程看作随时间变化、在一定控制范围内的灰色过程,把杂乱的原始数据整理成规律性强的生成数列进行数据生成,从而尽可能地降低仪器、人为误差给施工控制工作带来的影响。
(2)通过统计三元路淠河总干渠桥左幅1~5节段的箱梁底板实测误差来预测6节段的灰色模型数值,并修正立模标高从而降低误差。从计算结果来看,灰色体系理论是可行的。
