铁路波形钢腹板PC组合梁桥剪力滞效应分析

陈雨阳， 王佐才,2， 王书航

(1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009;2.土木工程防灾减灾安徽省工程技术研究中心，安徽，合肥 230009)

0 引 言

剪力滞效应是箱梁中普遍存在的现象，按照初等梁理论，箱梁在承受弯曲荷载时顶底板正应力分布均匀。但实际上，由于翼缘板上剪力分布不均匀，造成翼缘板纵向剪切变形也是不均匀的，由于翼板剪切变形不均匀造成的弯曲正应力沿梁宽方向不均匀分布的现象称为箱梁的剪力滞效应[1]。对于不同类型的桥梁，剪力滞效应会使主梁截面正应力分布变得难以确定，因此对目标桥梁进行剪力滞分析具有重要意义。

国内外学者对于剪力滞效应进行了较为广泛的研究，目前剪力滞分析方法主要有卡曼理论、弹性理论解法、能量变分法、比拟杆法和数值计算法等[2]，其中能量变分法通过引入剪力滞翘曲位移函数，建立了考虑剪切变形的截面横向位移分布模式，具有推理明确、计算方法与初等梁理论能较好地对应等优点，是目前剪力滞效应理论研究中应用最为普遍的方法。瑞斯纳[3](E.Reissner)运用能量变分法结合最小势能原理假设翼缘板剪力滞翘曲位移函数为二次曲线，成功得到集中荷载和均布荷载作用下双轴对称箱梁剪力滞效应的变分解；郭金琼等[4]将E.Reissner提出的翼缘板二次剪力滞翘曲位移函数修正为三次翘曲位移函数，推导出对称带伸臂的单箱单室箱型截面翼缘板的应力分布及其剪力滞系数方程；罗旗帜[5]引用了郭金琼的计算假定，将有限元法与能量变分法结合，提出了适用于计算变截面箱梁剪力滞效应的有限段法；魏丽娜等[6]基于单箱单室箱梁翼缘板翘曲位移函数分别为三次、四次抛物线分布的假定，利用当量截面法推导出变截面连续箱梁的剪力滞效应计算公式；吴文清等[7]通过将能量变分法与有限元法相结合，对简支箱梁的剪力滞效应进行了细致的参数分析。对于等截面箱梁的剪力滞效应，已经形成较为成熟的计算理论，而对于变截面连续箱梁的剪力滞效应计算，虽多位学者从不同的角度进行了深入的研究并取得较大突破，但并未形成较为体系的计算分析理论，计算方法存在缺陷，无法广泛适用于工程实践，目前变截面连续箱梁剪力滞效应多以有限元法进行分析。

波形钢腹板PC组合梁在我国的应用日益广泛，其保留了钢混组合结构的一般优点，在受力方面，主梁的抗弯抗剪性能合理分配，材料利用效率得到较大提升[8]；在施工方面，主梁自重减轻能够解决梁段运输难题，为桥梁的全预制装配式施工提供了新的思路。目前我国的波形钢腹板PC组合梁桥主要应用于公路桥梁中，鲜见铁路波形钢腹板PC组合梁桥。本文以(40+64+40) m有砟轨道预应力混凝土连续梁为背景，设计等跨径的铁路波形钢腹板组合箱梁桥，并基于有限元分析软件ANSYS对所设计的铁路波形钢腹板PC组合箱梁的剪力滞效应进行分析。

1 铁路波形钢腹板组合箱梁设计及基本受力分析

1.1 设计背景

本文的设计背景基于中铁第四勘察设计院于2008年编制的《时速250 km客运专线铁路有砟轨道预应力混凝土连续梁(双线)铁路工程建设通用参考图》，该连续梁桥全长145.2 m，计算跨径为(40+64+40)m，如图1所示，跨中和支点截面构造如图2所示。

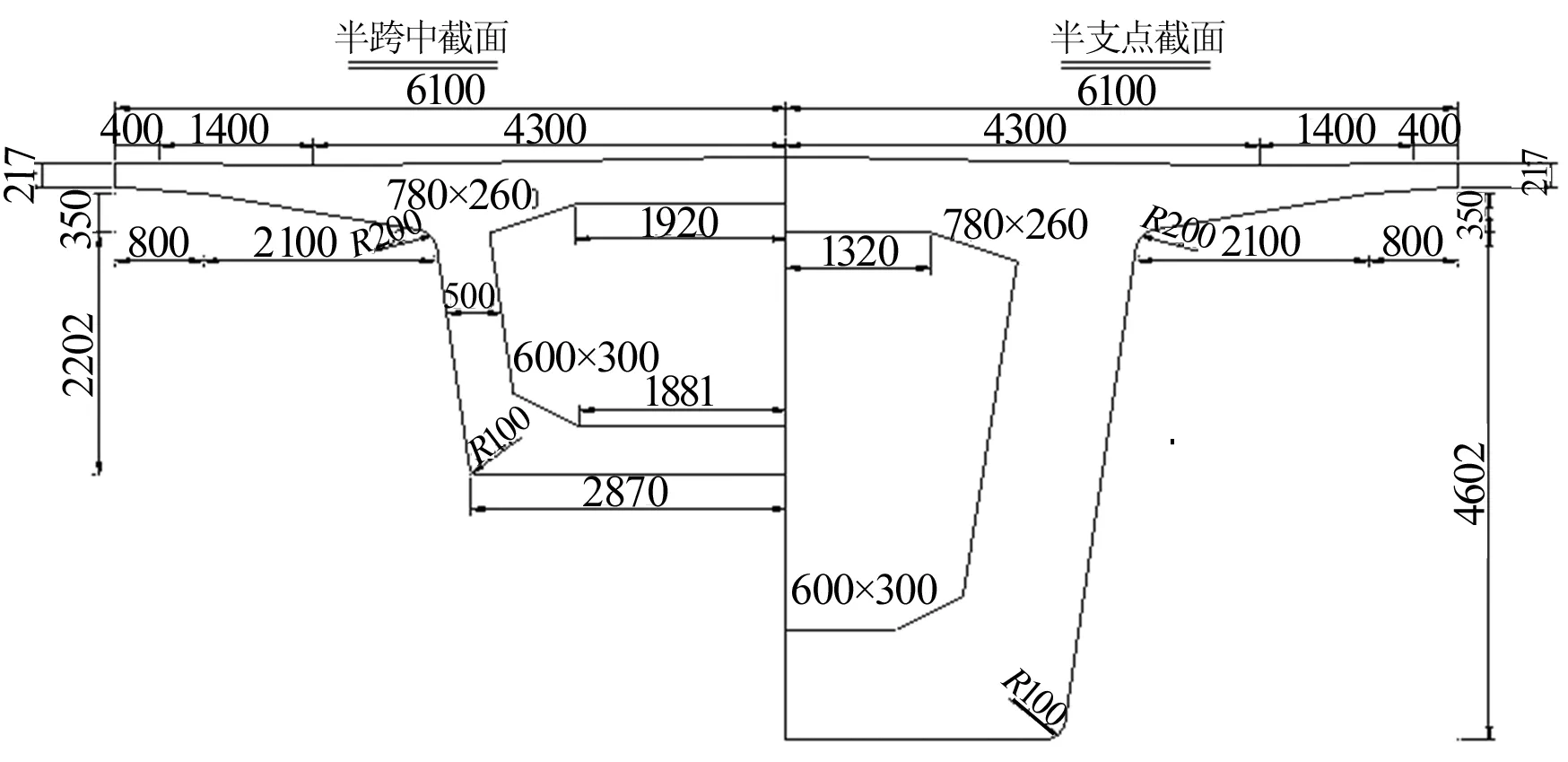
图2 混凝土梁跨中和支点截面断面图(单位:mm)

图1 混凝土连续梁桥立面图(单位:mm)

1.2 铁路波形钢腹板组合箱梁设计

相比于公路桥梁，铁路桥梁设计荷载较大，对于桥梁的横向及竖向刚度有较高要求。目前，国内尚无可供参考的铁路波形钢腹板组合箱梁桥的设计经验，本文以(40+64+40)m铁路混凝土连续梁桥为依据，考虑实现全预制装配式施工方法，设计铁路波形钢腹板组合箱梁桥。

1.2.1 截面尺寸拟定

以混凝土连续箱梁为参照,设计波形钢腹板连续箱梁截面。设计原则为：

(1)波形钢腹板PC组合梁顶底板厚度与原混凝土梁腹板截面变化相近。

(2)波形钢腹板PC组合梁腹板由原来的混凝土梁斜腹板替换为1200型波形钢腹板。

(3)为了方便主梁预制装配式施工，将波形钢腹板箱梁截面底板设计为等宽。

最终设计的波形钢腹板PC组合箱梁跨中及支点截面尺寸如图3所示。

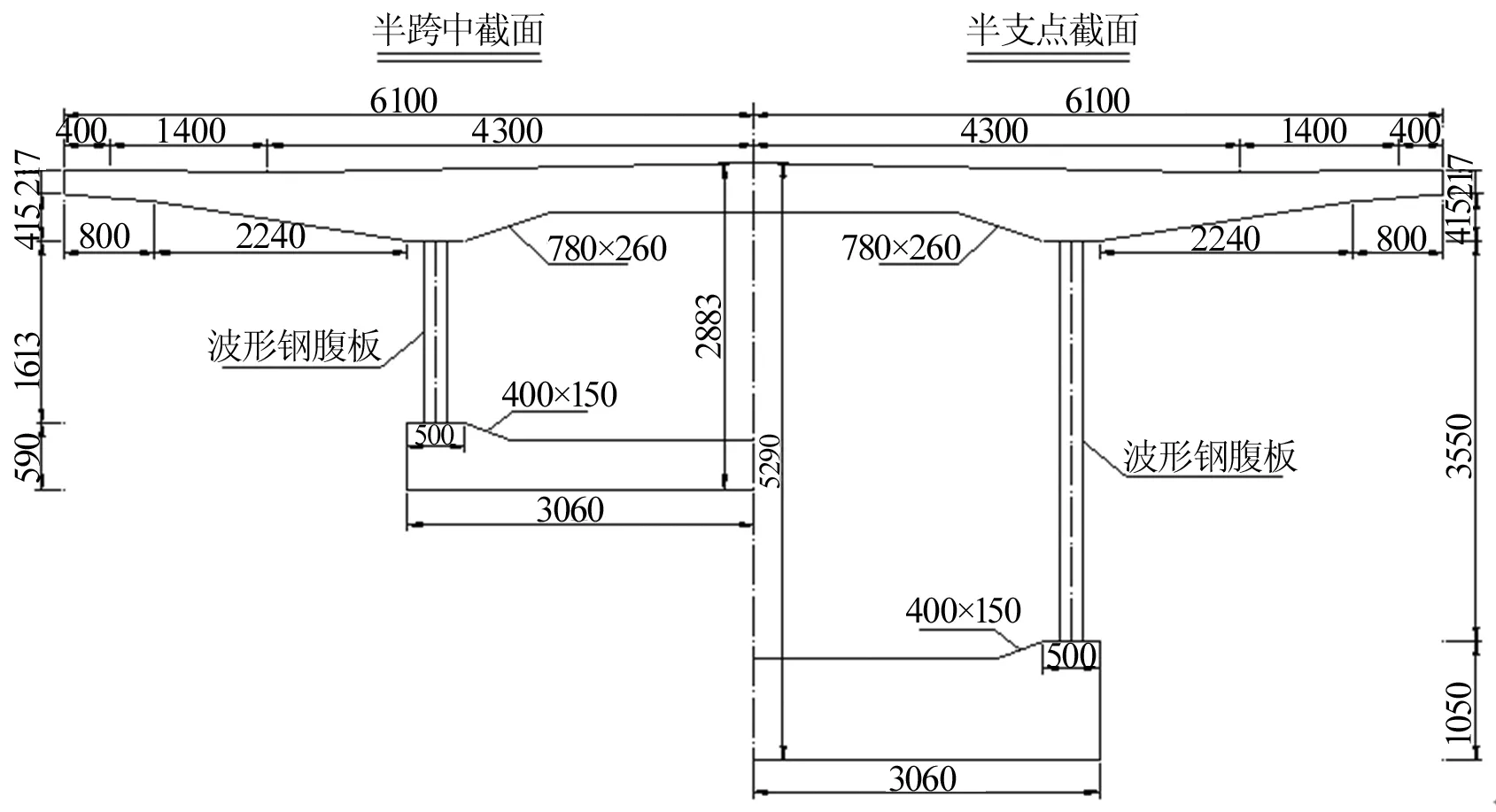
图3 波形钢腹板梁跨中和支点截面断面图(单位:mm)

设计参数为：顶板与原混凝土梁一致，宽12.2 m，厚0.43 m；底板宽6.12 m，横向保持水平；箱梁支点截面梁高5.29 m，跨中截面梁高2.89 m，按照1.8次抛物线变化；底板厚度由0.44 m到0.9 m，同样按照1.8次抛物线变化；波形钢腹板板厚参考日本黑部川大桥,按照16～22 mm从跨中到根部变化；翼缘板悬臂长为3.29 m，端部厚0.217 m，根部厚0.633 8 m(考虑2%横坡)；顶底板梗腋尺寸分别为0.78 m×0.26 m、0.4 m×0.15 m。

1.2.2 波形钢腹板尺寸拟定及节段划分

考虑到预制装配式施工过程中运输车辆尺寸限制，结合常用的波形钢腹板型号，选用1200型波形钢腹板，如图4所示。此种波形钢腹板为1.2 m一个波段，为使与原混凝土梁等跨径，将主梁划分为16个节段，主要节段为2.4 m一段，具体节段划分如图5所示。

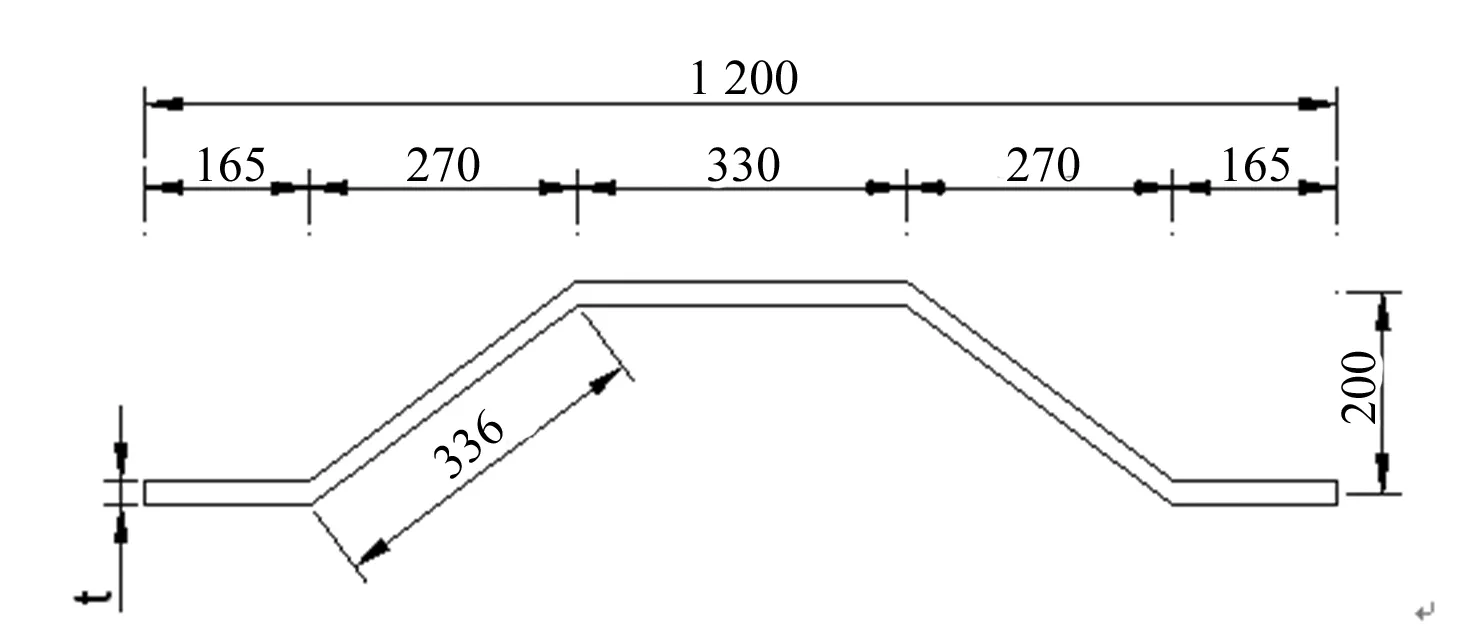
图4 波形钢腹板构造图(单位:mm)

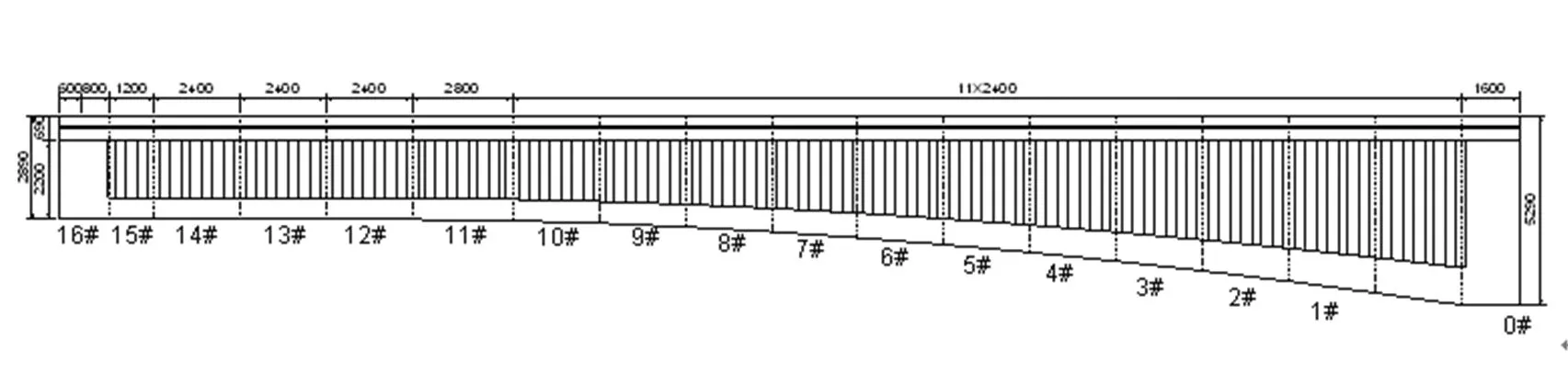
图5 波形钢腹板主梁边跨立面图(单位:mm)

1.3 波形钢腹板组合梁桥和混凝土连续梁桥基本力学性能对比

为验证上述设计的铁路波形钢腹板组合箱梁桥的可行性，利用MIDAS有限元分析软件分别建立了混凝土连续梁桥与波形钢腹板桥的力学分析模型，如图6、图7所示。

图6 混凝土连续梁桥MIDAS模型

图7 波形钢腹板箱梁MIDAS模型

对两种桥的基本力学性能进行分析，主要包括关键施工阶段的应力对比及主梁刚度对比，应力计算考虑预应力及自重荷载，计算结果见表1、表2。

表1 关键施工阶段主梁应力对比(单位：MPa)

表2 成桥状态主梁最大竖向位移(单位：cm)

由计算结果可知，波形钢腹板箱梁的应力略大于混凝土箱梁，两种桥梁在各关键施工阶段的应力较为接近；通过竖向挠度可知，波形钢腹板主梁竖向刚度小于混凝土连续梁，但在列车荷载作用下，其竖向挠度仍然满足设计规范的要求，初步验证了所设计波形钢腹板组合箱梁桥的合理性。

2 铁路波形钢腹板组合箱梁剪力滞效应有限元分析

2.1 有限元模型建立

为分析变截面波形钢腹板箱梁剪力滞效应，本文运用大型通用有限元软件ANSYS建立全桥的实体分析模型，分别分析主梁各关键截面在集中荷载和均布荷载作用下的剪力滞效应。

主梁混凝土顶底板采用8节点实体Solid 65单元模拟，波形钢腹板采用4节点壳单元Shell 43模拟[10]；采用MPC壳-体接触装配法，建立接触单元Targe 170和目标单元Conta 175形成接触对，模拟混凝土顶底板与波形钢腹板之间的连接[11]；网格划分采用映射网格划分，为方便分析处理，将混凝土顶底板按照波形钢腹板波段用工作平面切分；约束施加与原混凝土连续梁的设计支座约束保持一致。本次计算未考虑预应力作用，最终计算模型由171 552个节点，137 660个单元组成，如图8所示。

图8 变截面波形钢腹板箱梁ANSYS实体模型

2.2 剪力滞效应分析

为分析变截面波形钢腹板组合箱梁桥在纯外荷载作用下的剪力滞效应，本次计算取集中荷载和均布荷载两个工况加载计算，各工况加载图示如图9所示，其中P=360 kN，q=25 kN/m。

a.工况一(集中荷载)

b.工况二(均布荷载)

在集中荷载和均布荷载分别作用下，变截面波形钢腹板组合箱梁中跨跨中截面、根部截面剪力滞效应如图10～13所示。

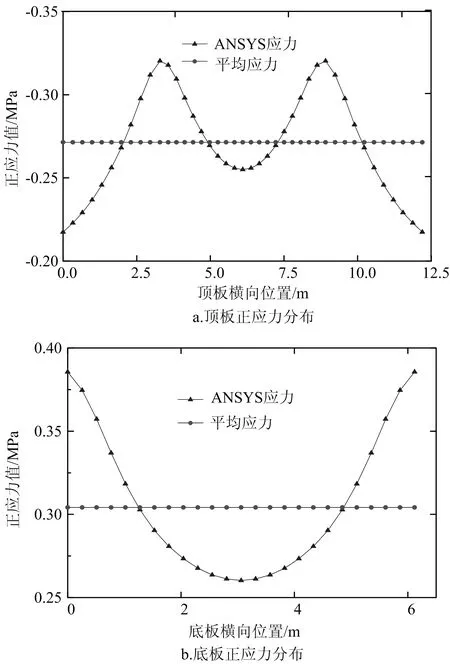
图10 工况一中跨跨中截面正应力分布

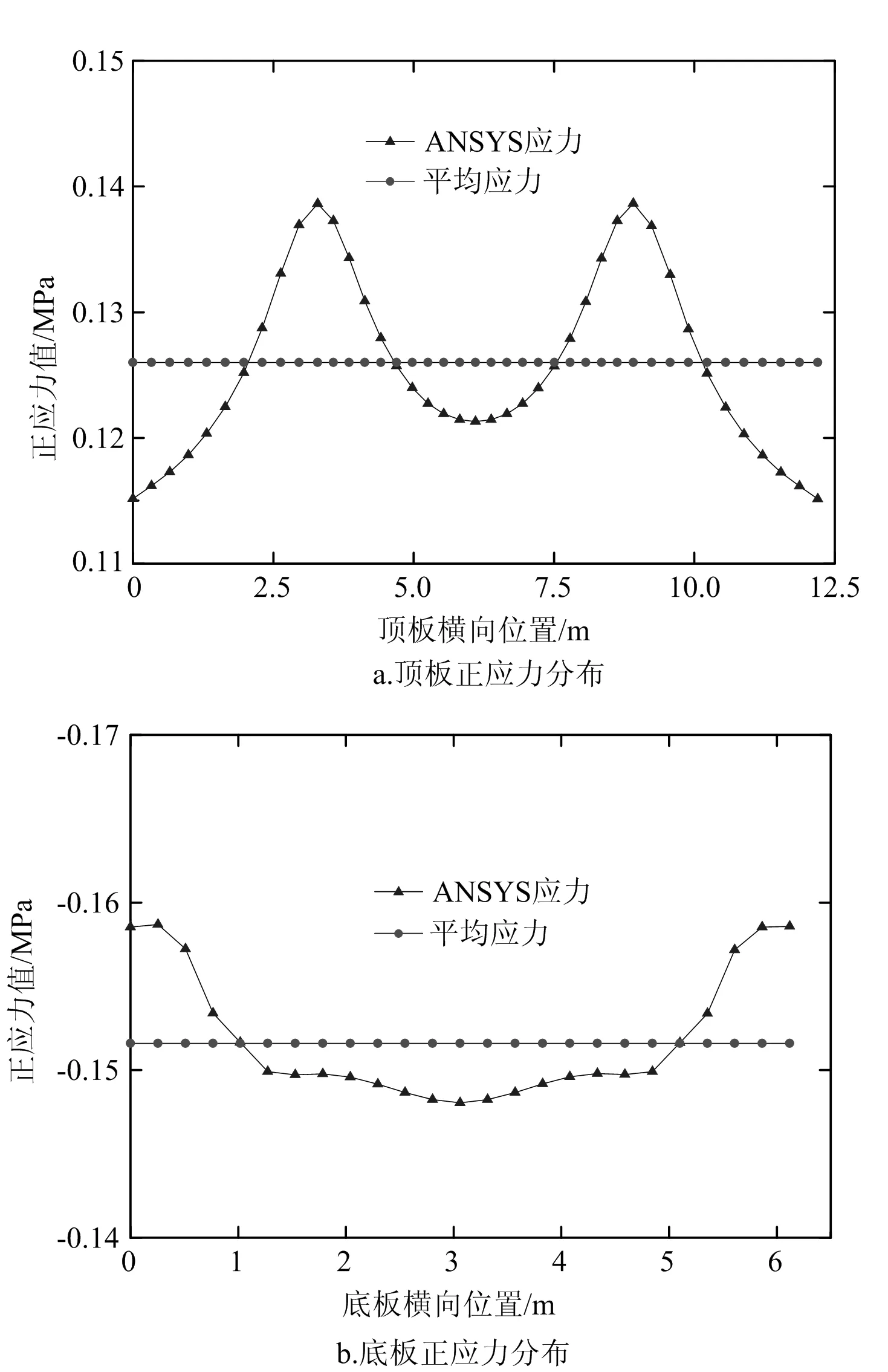
图11 工况一中跨根部截面正应力分布

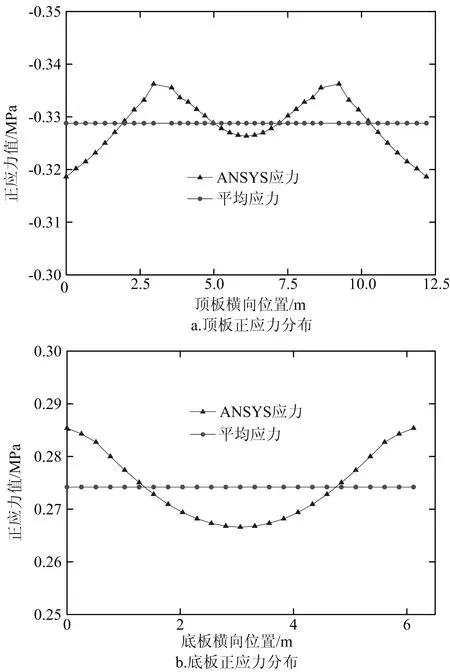
图12 工况二中跨跨中截面正应力分布

图13 工况二中跨根部截面正应力分布

图中平均应力为翼板正应力图与坐标轴围成的面积除以翼缘板宽度得到，此平均应力近似为按初等梁理论计算所得的正应力值。由以上计算结果可知，无论在集中荷载还是在均布荷载作用下，中跨跨中截面和中跨根部截面腹板位置处均产生了明显的正剪力滞效应。

通常情况下，翼板在腹板附近处出现正应力峰值，在计算过程中，发现外力的加载点位置处会产生应力集中效应，这对于剪力滞系数计算在一定范围内影响较大。对于工况一，本文采用在顶板作用集中荷载计算底板剪力滞系数和在底板作用集中荷载计算顶板剪力滞系数的方法，避免了集中荷载的应力集中效应对于加载截面剪力滞系数计算的影响，计算结果反映了桥梁自身结构特性在外荷载作用下产生的剪力滞效应；对于工况二，在计算顶板剪力滞效应时，采用应力集中突变点之外的各点计算截面的剪力滞效应，由于均布荷载采用面荷载满布全桥两侧腹板处的桥面，近似认为其在各加载面处产生同样的应力集中效果，对于各截面的剪力滞系数计算有同样的影响，此种情况下计算的剪力滞系数适用于同一研究对象的各截面剪力滞系数横向对比分析，计算出来的剪力滞系数符合实际工程应用中的加载效果，具有实际意义。

为分析全桥各关键截面的剪力滞系数变化规律，本文选取边跨跨中、边跨3/4、边跨根部、中跨根部、中跨1/4、中跨跨中截面作为剪力滞系数计算的各关键截面，计算结果如图14所示。

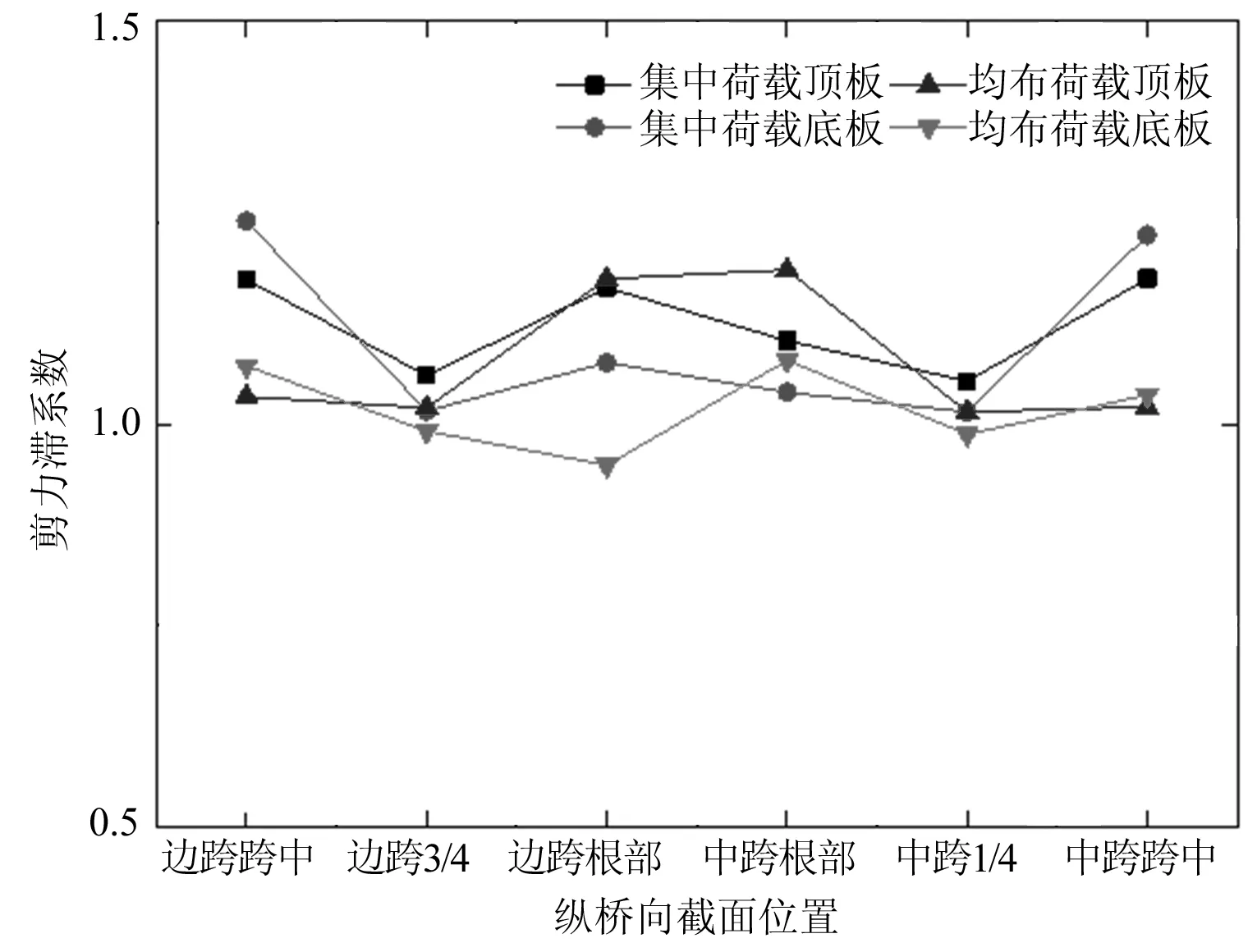
图14 波形钢腹板箱梁各关键截面剪力滞系数

由计算结果可知，在集中荷载作用下，各关键截面均出现了不同程度的正剪力滞效应，其中边跨跨中和中跨跨中截面的剪力滞效应较为明显，顶底板剪力滞系数变化规律一致。均布荷载作用下，顶板根部截面剪力滞效应大于其他关键截面，底板边跨根部和中跨根部截面剪力滞效应不同，其中边跨3/4、边跨根部、中跨1/4截面底板出现负剪力滞效应。

3 变截面波形钢腹板与混凝土腹板连续梁桥剪力滞效应对比分析

本文变截面波形钢腹板组合箱梁桥参照混凝土连续梁桥设计而来，因此有必要对两者的剪力滞效应进行对比分析。利用ANSYS有限元软件建立混凝土连续梁桥的实体模型，主梁同波形钢腹板箱梁顶底板采用8节点实体Solid 65单元模拟，最终计算模型由112 810个节点，81 480个单元组成，如图15所示。

图15 变截面混凝土箱梁ANSYS实体模型

分别选取集中荷载和自重荷载作为两种桥梁剪力滞效应对比分析的荷载工况，其中集中力荷载工况分析两种桥梁在同一外力作用下单纯由于自身结构不同产生的剪力滞效应，计算截面选取边跨跨中、边跨根部、中跨根部、中跨跨中4个关键截面进行分析，计算各关键截面腹板处剪力滞系数；自重荷载工况分析两种桥梁在实际工程应用由于自身综合特性不同产生的剪力滞效应差异。由于对称性，计算截面选取全桥一半截面进行分析，计算各截面最大剪力滞系数。

在集中荷载作用下，两种类型桥梁的各关键截面腹板处剪力滞系数分布如图16所示。

图16 集中力作用下箱梁各关键截面剪力滞系数

由计算结果可知，本文设计的变截面波形钢腹板箱梁在各关键截面腹板处顶底板剪力滞系数均大于原混凝土箱梁。

在自重荷载作用下，波形钢腹板箱梁与混凝土箱梁全桥各截面顶底板最大剪力滞系数分布如图17所示。

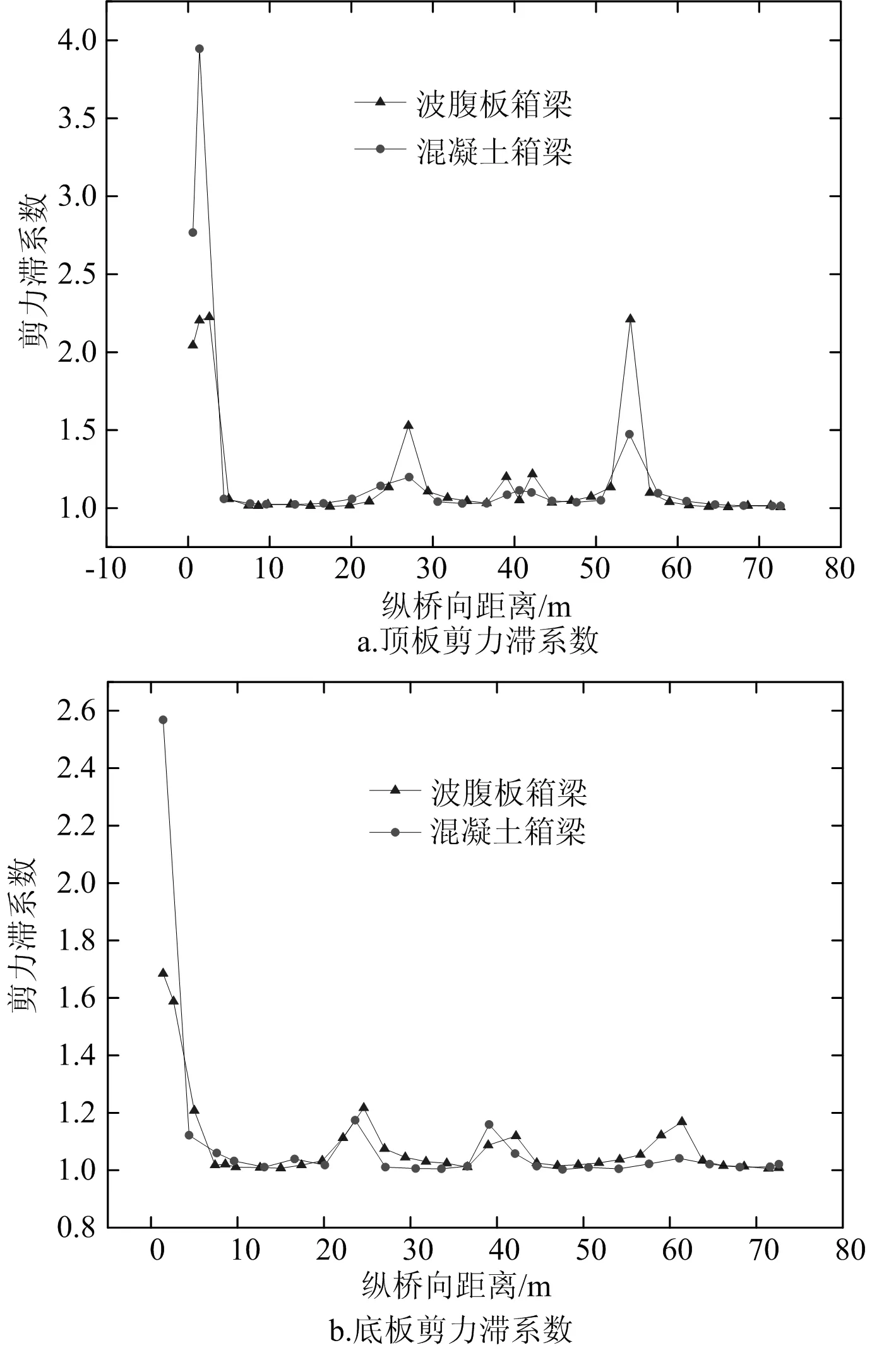
图17 自重荷载作用下箱梁全桥最大剪力滞系数

总体来看，在自重作用下，波形钢腹板箱梁与混凝土箱梁的全桥各截面顶底板最大剪力滞系数分布规律趋于一致；在边支点、边跨3/4、边跨根部、中跨根部、中跨1/4附近截面最大剪力滞系数出现增大的现象，这是由于这些截面靠近弯矩为0但剪力不为0的截面附近，理论上这些截面会出现剪力滞系数突变的现象；波形钢腹板箱梁与混凝土箱梁的全桥剪力滞系数大小交替变化，但在剪力滞系数变大的区域，除边支点外，波形钢腹板箱梁的最大剪力滞系数呈现比混凝土箱梁大的趋势，在设计时应充分考虑这些截面的剪力滞效应。

4 结束语

随着我国高速铁路的飞速发展，在环境复杂的地区，预制装配式桥梁具有非常明显的经济及技术效益，波形钢腹板箱梁自重轻，受力性能好，是适应于预制装配式施工的极具竞争力的桥梁结构。本文立足于铁路桥梁，在传统(40+64+40)m通用混凝土连续箱梁桥的基础上设计了铁路波形钢腹板PC组合箱梁桥，通过建立有限元模型对两者的基本力学性能进行分析，结果初步表明铁路波形钢腹板箱梁桥具有应用工程实践的可行性。

本文运用有限元法计算了波形钢腹板箱梁在集中荷载和均布荷载作用下的主梁各关键截面剪力滞系数，并对波形钢腹与混凝土腹板连续梁桥在不同荷载工况下的剪力滞效应进行了对比分析。分析结果表明，总体上看，不论在何种荷载作用下，本文所设计的波形钢腹板箱梁在各关键截面的剪力滞效应大于混凝土箱梁；箱梁的剪力滞效应主要与外荷载的作用形式及结构自身的几何特性相关，在进行剪力滞分析时，应对所研究的目标桥梁进行针对性的分析。