特斯拉阀单向导通性研究

刘海洋 马 佳 王 森 郑若雨

(沈阳航空航天大学 1创新创业学院; 2理学院，辽宁 沈阳 110136)

1 问题的提出

特斯拉阀起源于尼古拉·特斯拉在1920年提出的无可动部件阀专利[1]，这是一个有固定几何形状的单向阀门，可以对内部流体提供一个方向相较另一个方向大得多的流体阻力。相较于传统阀，特斯拉阀无可动部件，因此使用寿命更长，且便于批量生产。特斯拉阀在微流体控制系统，开发无可动部件阀门等方面有潜在应用价值，因此具有较大的研究意义。

目前有诸多工作者对此进行了一系列的研究，如Reed. J. L在尼古拉·特斯拉提出的结构基础上，通过进一步改进，提出了MSTV型特斯拉阀[2]；Gamboa. A. R等人计算得到了GMF型特斯拉阀单元结构[3]，能够有效提高特斯拉阀单向导通效率；Bardel.R.L提出了表征特斯拉阀单向导通的参数Di[4]；S. Zhang等人则提出了可能影响效率参数的7个结构参数[5]。

而前人所做的工作集中在微流体控制系统中μm级别尺寸的特斯拉阀，在较大尺寸结构的相关特性方面有所欠缺。我们希望能对特斯拉阀的应用领域做出推广，因此，从经放大100倍且具有最佳单向导通特性的GMF特斯拉阀出发，使用当今成熟的计算流体动力学(CFD)技术，并结合实验分析，对影响其特性的相关因素进行了探讨。

2 特斯拉阀相关理论

2.1 GMF特斯拉阀

特斯拉阀最早由尼古拉·特斯拉提出，经前人研究后，得出的具有最高单向导通效率的结构为GMF特斯拉阀[3]，其单元示意图如图1所示。

图1 GMF特斯拉阀单元(长度单位：mm)

特斯拉阀单元可视为由3个通道组成，直通道，圆弧通道和斜通道，现有大多数研究所使用的通道深度为100μm，为探讨经放大100倍后结构的相关特性，本研究所设定的通道深度为10mm。直通道与斜通道的夹角为48°，圆弧通道分别与直通道，斜通道过渡连接，且通道外圆弧半径为23.53mm，直通道，斜通道中未与其他通道汇交的部分长为120mm。

2.2 正向流动与逆向流动

如图1所示，通道左端和右端端口均可作为流动的入口和出口，定义为左端为正向流动的入口，右端为逆向流动的入口。正向流动方向指的是流体流动过程中所受阻力较小的方向，逆向流动方向则为阻力较大的方向。本文给出使用有限元分析软件ANSYS v17.0的CFX后处理模块，在入口处流体流量为6·min-1等边界条件下，得到的正逆向流动速度云图，如图2和图3所示，具体的实现原理与过程将在第3节介绍。

图2 正向流动速度云图

图3 逆向流动速度云图

从图2和图3的速度分布可以看出，正向流动时流体将沿水平通道和倾斜通道流至出口，逆向流动时沿倾斜通道流至圆弧通道，最后沿水平通道流出。这是由于在流体流动中，流动方向的突然改变会产生很大的阻力，因此流体更趋向于沿通道中变化较为平缓的方向流动。

其中，结构在圆弧通道和水平通道的汇交处有较大的几何突变，逆向流动时流体不得不流经此区域，这个过程需要克服很大的阻力，因此导致逆向流动比正向流动更为困难。

2.3 单向导通性参数

Bardel.R.L所提出的表征特斯拉阀单向导通性的参数Diodicity，数值上等于逆向流动压降与正向流动压降的比值[4]，表达式为

(1)

其中，Di代表Diodicity；ΔPf为正向流动时通道产生的压力降；ΔPr为逆向流动时通道产生的压力降。Di值越大，意味着逆向流动比正向流动更为困难，阀的单向导通效果就越明显。

3 CFD数值计算与实验建立

下面通过数值计算与实验相结合的方法，以Di值的大小作为判断标准，探讨影响特斯拉阀单向导通性的相关因素。

3.1 CFD数值计算

3.1.1 计算模型

流体在特斯拉阀中的流动是三维流动过程，描述运动的方程可由质量守恒定律，动量守恒定律推出[6]。

1) 质量守恒

质量守恒定律可表述为单位时间段内有限控制体总质量变化量等于单位时间内外界流入有限控制体的流体质量，因此质量守恒方程可表述为

(2)

其中，ρ为流体的密度；V为合速度矢量，在x，y，z3个方向的分量分别为u，v，w；di()为散度运算符，对于给定矢量a，div(a)=∂ax/∂x+∂ay/∂y+∂az/∂z。

2) 动量守恒

动量守恒方程实际是牛顿第二定律在流体力学中的体现，可表述为：作用在流体微元上外力的合力等于单位时间内流入流体微元中流体动量的增量。据此可得到x，y，z3个方向的动量守恒方程：

(3)

(4)

(5)

其中，grad()为梯度运算符，对于给定标量a，grad(a)=∂a/∂x·i+∂a/∂y·j+∂a/∂z·k；μ为动力黏度；p为流体微团上的压力；Fx,Fy,Fz为作用在流体微团上3个方向的质量力。

3) 通用方程

比较方程(2)～(5)，可以看出，这些方程均反映了单位时间体积内物理量的守恒性质，所有方程均可表示成如下通用形式：

(6)

其中，φ为通用变量，可以代表u,v,w等求解变量；Γ为广义扩散系数；S为广义源项。

上述方程经过简化，均可化为通用形式的偏微分方程，求解时只需要考虑通用方程(6)的数值解，对于不同的φ，只需给定Γ和S的适当表达以及适当的边界条件，便可求解[6]。

3.1.2 边界条件

对于任何流场问题，都需要给定边界条件，使得上述偏微分方程可解，本文中设定入口边界设定为流量条件，出口边界为静压条件，参考压力为0Pa，并设定内壁为无滑移壁面，即靠近内壁位置的流体流速为零。

3.1.3 求解计算

求解过程为通过数值方法求解偏微分形式的流体动力学方程的过程[8]。对于水这种流体，可视为不可压流体[8]，密度ρ不随时间和空间变化，因此上述方程中仅存在u，v，w，p4个未知量。通过联立方程(2)～(5)，转化为如式(6)所示通用形式，并引入上述边界条件，便可对其进行求解。所得的结果可对计算区域内各个位置的速度和压强进行描述，进而我们可以从中获得入口处压力值。由于设定的参考压力为0Pa，所以入口处的压力值也代表了入口处与出口处压力的差值，分别按照正向流动和逆向流动的方向设定出入口，便可得到ΔPf和ΔPr，分别计算并代入式(1)，便可得到通过数值方法求解的单向导通参数Di。

3.1.4 后处理

后处理的作用是便于使用者有效地观察和分析流动计算结果[6]，它可以显示各求解量随时间，空间的变化情况，显示方式包括等值线方式，矢量线方式等。本文图2和图3便结合了等值线和矢量线，对所求合速度矢量V的空间分布进行了展示，方便了上文向读者阐述流体在特斯拉阀中正逆向流动的现象及区别。

3.2 实验方法

实验用到的器材有(见图4)：高精度数字流量计、高精度数字压力表、胶皮管、3D打印特斯拉阀模型。

图4 实验装置

将实验装置中靠近流量计的一端连接水龙头，靠近特斯拉阀模型的一端水平放置。调节水龙头水流大小，使流量计显示数值与设定值相同，待水流稳定后，每隔10s读取一次压力表示数，连续测量十次后取均值，将均值视为实验测得的入口处压力值，分别将模型的两端作为入口，便可得到实验测得的ΔPf和ΔPr，再代入式(1)，便可得到由实验数据计算而来的效率参数Di(见表1)。

4 结果与讨论

4.1 单向导通率与流量关系

从图5和图6看出，随着流量的增大，正向流动压降和逆向流动压降均呈增长趋势，且增长速度逐渐加快，这是由于流量越大意味着流速越大，而通道中的沿程阻力和局部阻力均与流速的n次方成正比(n>1)[7]，最终导致流量越大，阻力越大。通过比较纵坐标，发现逆向压降增长速率要超过正向压降，说明流体逆向流动时会比正向流动更为困难。由式(1)得到的数值计算Di值和实验计算Di值，如表1所示。

图5 不同入口流量对正向流动压降的影响

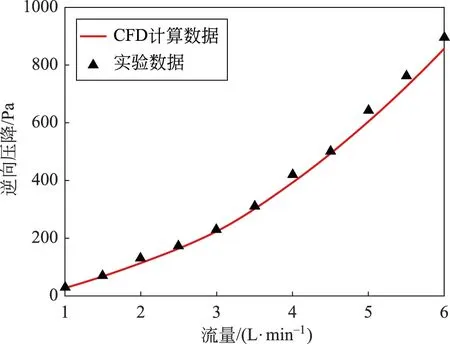
图6 不同入口流量对逆向流动压降的影响

从表1中数据可以看出，无论是数值计算结果还是实验结果，Di值均大于1，说明经放大后的特斯拉阀依旧保留着单向导通的特性。当入口流量从1(L/mi)逐渐增加至6(L/min)的过程中，Di值在1.7～2.0范围内波动。

表1 CFD计算与实验计算Di比较表

实验数据与数值计算结果存在一定的误差，其中实验误差的主要来源是所用的3D打印模型，模型内壁由于制作原因并非光滑壁面，与理想情况下的数值结果相比，流体流过时会产生更多的沿程损失，因此实验测得的正逆向流动压降略大于数值计算数据，且随入口流量的逐渐增大，此部分沿程损失也会进一步增大，因此导致了表1中相对误差整体上呈增长趋势。数值计算结果也会由于网格划分等方面产生较小误差，但与实验误差相比，可忽略不计。总体看来，数据最大误差仅为4.57%，足以说明数值计算结果与实验结果符合较好。

4.2 单向导通率与单元个数关系

采用如图7所示的组合方式，探讨单元个数对单向导通效率的影响。

图7 多单元特斯拉阀组合方式(单元数等于4)

在保证入口流量为3(L/min)的前提下，分别使用单元个数为1、2、4、6、8、10的多单元特斯拉阀进行实验，并与CFD数值计算结果进行对比，所得结果如图8所示。

图8 不同单元个数对Di的影响(入口流量为3L/min-1)

由图8可知，随着单元个数的逐渐增加，无论是CFD计算结果还是实验结果，特斯拉阀的单向导通效率均逐渐增大，这是由于每个单元都会对流体产生阻碍作用，单元数目的增多会产生叠加的效果。通过观察纵坐标，还可以得出单元个数的改变将对单向导通效率产生较大影响，因此增加单元个数是提高特斯拉阀效率的一个有效措施。

5 结语

以放大100倍的GMF特斯拉阀为研究对象，采用CFD数值计算和实验的方法，通过比较数值计算结果与实验结果，探讨了入口流量和单元个数对单向导通效率的影响。尽管实验仪器会对实验结果产生一定的影响，但在误差允许的范围内，数值计算结果与实验结果能较好符合。入口流量和单元个数将对特斯拉阀单向导通效率产生较大影响，增加单元数目可显著提高特斯拉阀的单向导通效率。该研究结果可为特斯拉阀应用领域的推广起到借鉴作用，也可为对此方面感兴趣的研究人员提供参考。