巧借画图，提升解题能力

文玉英

(广东省清远市新北江小学 广东 清远 511500)

综所周知，画图策略是解决问题最基本的策略之一。实践也证明，画图具有直观性、形象性、实用性，如果学生从小掌握了用画图辅助解题的方法，分析问题和解决问题的能力将会有大大的提高，对今后的学习生活将有很大的帮助。苏霍姆林斯基也曾说过：“如果哪一个孩子学会了“画”应用题，我就可以有把握地说，他一定能学会解应用题”。那如何让学生在日常的学习中掌握画图策略，提升自己的解题能力，现结合自己的教学实践谈谈体会。

1.借图之力，突破解题关口

解题成功的关键是能及时准确地找到解题的突破口，如何寻求解题的突破口？我们不妨用画图试着去分析，可能会出现“柳暗花明又一村”。因为许多数学问题，光凭借看到的信息不易解决，还得靠挖掘利用深层次的数量关系才行。而挖掘深层次数量关系的过程往往就是寻找解题思路的过程，深层次的数量关系一旦找到，便为解题提供了新的信息与依据，解题思路也就随之而生，因而我们可以借助画图，寻找解题突破口，叩开解题之门。

例如：在一个直角三角形中，两个锐角之差是18度，这两个锐角各是多少度？

面对这道题很多学生束手无策，经访谈发现他们很多会发现两个锐角之和是90度，但就会停滞于此，无法前进。这时我们不妨引导学生通过画一画把两个锐角之间的关系画出来。(如图1)再让学生仔细观察说发现。若孩子们还是有困难，老师可以做个手势(挡住多出的部分)，说“假如……”，经这一提醒相信孩子们会茅塞顿开，解题的突破口找到了，解题方法就会自然而然的出来了。

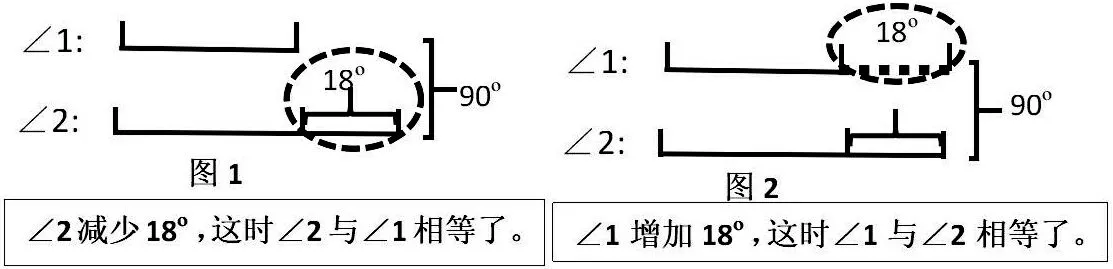
在此基础上，让学生再次观察图形，想想还可以怎样计算，(如图2)有了之前的经验，第二种方法相信会很顺利的迁移过来。

2.借图之形，优化解题过程

一道题的解法有时往往是多种的，但有的是可行但不可取。正如我们要到达一个目的地，路线的选择有很多，这时就需要我们综合各种因素去规划一条最佳的路线。解题也是如此，而数形结合正是优化解题常用的方法，它可以利用图形的直观性突显出所求的问题。

例如：“一个长方形菜地的长是10米，宽是6米，现菜地要进行扩建，把长延长了5米，这个长方形的周长增加了几米？”

当读完题目后,大部分学生应该很快会想到现在菜地的长变为：10+5=15(米)，就先算现在菜地的周长:(15+6)×2=42(米),再算原来菜地的周长：(10+6)×2=32(米)，最后用现在菜地的周长减去原来菜地的周长：42-32=10(米)。很多老师可能到此就结束了这道题，认为学生都会解答了没必要再讲了。其实我们更应该在此“画龙点晴”，让学生先画图表示出题意，然后让他们仔细观察再思考还有没有别的方法来解答这道理,经此引导相信有不少学生会眼前一亮。

在学生充分交流后，教师再利用课件进行动画演示，让学生明白原来的一条宽因在里面了，不再是现在菜地的周长，可以想像把它平移到外面,那这样对比之下这个长方形的周长只是增加了两段5米，因此可以直接列式为：5×2=10(米)。两种方法对比之下，可见第二种方法更快捷方便。

3.借图促思，探索解题多样化

一题多解不仅能巩固基础知识，而且能深刻提示问题的内在本质属性，多层次、多角度地培养和锻炼学生的发散性思维。如何拓宽学生思路，促使学生思维多方面发展？我们可以借助图形让学生把数学信息直观地呈现出来，让他们在观察、比较、分析中探索出不同解决问题的方法。

例如，一个书架每层放25本，每个书架有4层，两个这样的书架一共可以放多少本书？

放书的问题中3个条件两两结合，它们的乘积都有实际的意义。但是学生在解决问题时，最容易想到的是“先求一个书架放多少本书？”，如果不借助直观图，学生很难想到其它方法，有的虽然列出了算式，但也理解不了它的算理。因此教学时可让学生读题的基础上自主画出直观图。

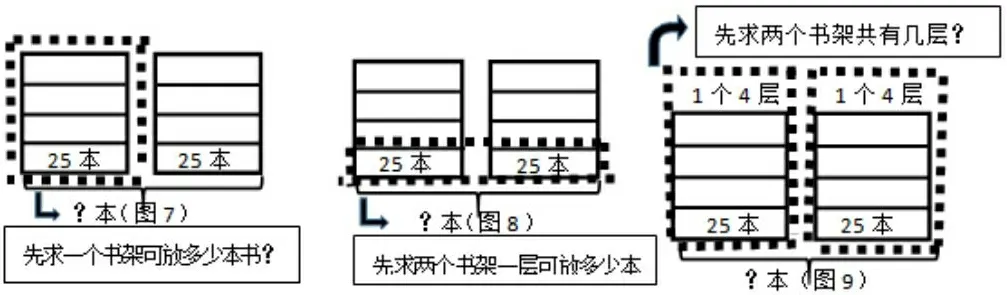
引导学生借助直观图从不同角度进行观察，思考，再通过圈一圈、标一标，思考可以求出什么问题，并引导学生进行交流。这时直观图就成了学生思考交流的“直观媒介”，利用图的直观表象可以有理有据地表述先算什么，再算什么，明确了不同的解题思路，感知了3种方法的实际意义，体会了解决问题策略的多样性。