转子体连杆轴定载下最大应变不确定度的评定

贾仕君, 吴嘉杰, 刘 杨, 巴发海

(上海材料研究所 上海市工程材料应用与评价重点实验室, 上海 200437)

在实验室质量体系中，测量结果不确定度的评定及应用非常重要[1]。目前关于金属材料力学性能试验的研究较多，主要是针对室温拉伸和硬度试验[2-16]，而关于金属结构件或实物件力学测量结果不确定度评定的研究较少。为评估结构件力学测量结果的可靠性，对其进行不确定度评定具有重要意义。为此，笔者采用万能拉伸试验机对转子体连杆轴结构件进行轴向加载，通过应变仪测量其在载荷为80 kN时连杆轴的最大应变，并进行了测量影响因素分析和不确定度评定，以供相关人员参考。

1 测量方案

1.1 测量准备

对转子体连杆轴表面进行打磨后粘贴BE120-3AA(11)型A级电阻应变片，粘贴位置如图1所示。实验室环境温度为(23±2) ℃，相对湿度为(50±10)%。

图1 电阻应变片粘贴位置Fig.1 Sticking position of resistance strain gauge

1.2 测量程序

通过特制工装将转子体连杆轴与ZWICK Z400型拉伸试验机连接，如图2所示。接通转子体连杆轴上电阻应变片和应变数据采集器，将拉伸试验机载荷清零，应变仪平衡清零，以恒定横梁位移速度2 mm·min-1对转子体连杆轴加载，采用DH3820型应力应变仪进行应变测试，当载荷超过80 kN时停止加载。重复测量10次。

图2 转子体连杆轴与拉伸试验机连接装置图Fig.2 Connecting device diagram of connecting shaft of rotorbody and tensile testing machine

2 数学模型

转子体连杆轴应变的测量受多种因素的影响，其中包括测量重复性，拉伸试验机、应变片、连接导线和测试环境引入的误差等，综合考虑上述因素建立如下数学模型。

ε=ε标+δ1+δ2+δ3+δ4

(1)

式中：ε为测试所得应变结果；ε标为标准模拟应变量校准器给出的标准值；δ1为测量重复性引入的误差；δ2为拉伸试验机力值示值引入的误差；δ3为应变片等级引入的误差；δ4为导线电阻和环境温度引入的误差。

3 不确定度来源及其评定分类

测量得到的应变结果受多种因素的影响，不同不确定度来源需要按照不同评定类别进行考虑。因此按照不确定度分析方法，对不同不确定度来源进行评定分类，如表1所示。

4 测量数据及不确定度评定

转子体连杆轴的应变测量数据如表2所示。

表1 不同不确定度来源及其评定分类Tab.1 Different uncertainties sources and evaluation classification

表2 转子体连杆轴的应变测量结果Tab.2 Strain measurement results of connecting shaft of rotor body με

4.1 输入量ε标不确定度分量的评定

根据应变仪校准报告，应变仪相对扩展不确定度Urel=3×10-4(k=2)。由此计算出ε标相对标准不确定度分量urel(ε标)为

urel(ε标)=1.50×10-4

(2)

4.2 输入量δ1的不确定度分量的评定

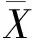
(3)

根据贝塞尔公式可得到标准差s(δ1)为

(4)

式中：xi为单次测量的应变值；n为测量次数。

输入量δ1的标准不确定度为

(5)

输入量δ1的相对标准不确定度分量urel(δ1)为

(6)

4.3 输入量δ2的不确定度分量的评定

(7)

4.4 输入量δ3的不确定度分量的评定

(8)

4.5 输入量δ4的不确定度分量的评定

应变测试系统的采集原理是通过测量应变片的电阻变化得到被测物的应变。该测试系统的测试桥电阻为120 Ω，连接应变片与采集系统的导线电阻为0.5～5 Ω。连接导线串入的额外电阻影响了测试桥电阻，因此连接导线引入了一个不确定度。应力应变仪测试系统的长导线修正范围为0～100 Ω，可以修正连杆导线串入的额外电阻，因而连接导线引入的不确定度可以忽略不计。

环境的温度和湿度也会影响电阻的测量，该试验环境为标准实验室环境，应力应变仪测试系统存在温度补偿模块，因而温度和湿度的影响可忽略不计，可得到输入量δ4的相对标准不确定度分量urel(δ4)为

urel(δ4)=0

(9)

4.6 合成标准不确定度的评定

(1) 灵敏度系数

根据数学模型式(1)可得

(10)

(11)

(12)

(13)

(14)

式中：c1～c5分别为ε标，δ1，δ2，δ3，δ4不确定度分量的灵敏度系数。

(2) 相对合成标准不确定度

由于上述分量各不相关，因此可求ε的相对合成标准不确定度ucrel(ε)。

(15)

可得

ucrel(ε)=4.11×10-3

(16)

通过代入最佳估计值，可以计算出ε的合成标准不确定度uc(ε)为

4.11×10-3×3 420=14 με

(17)

4.7 扩展不确定度的评定

根据扩展不确定度计算公式U=kuc，采用k=2，可计算得到ε的扩展不确定度U(ε)为

U(ε)=2×uc(ε)=28 με

(18)

4.8 不确定度报告

当转子体在轴向载荷为80 kN时，其连杆轴上最大应变ε(平均值为3 420 με)的扩展不确定度为28 με(k=2)。

5 试验结果

由上述不确定度分析，可得到转子体连杆轴的应变测量结果不确定度综合评定情况如表3所示。

表3 转子体连杆轴的应变测量结果不确定度评定情况Tab.3 Evaluation of uncertainty of the strain measurementresults on the connecting shaft of rotor body

6 结论

通过对影响转子体连杆轴的应变测量结果不确定度的来源及其相对标准不确定度进行分析和计算，得到其扩展不确定度为28 με。标准模拟应变量校准器给出的标准值、测量重复性、拉伸设备精度、应变片等级、导线电阻和环境温度对测量结果的准确性影响较大，其中拉伸设备精度和应变片等级的影响最大。建议在测试过程中严格按照操作规程进行试验，避免引入其他误差。